Navigation
- index
- next |
- previous |
- Home »
- The Benchmarks »
- SciPy Extended
 SciPy Extended¶
SciPy Extended¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| Yes | Yes | Easy |
All the test functions in this benchmark suite have been taken from the mathematical literature on Global Optimization. The test suite currently contains:
For the purpose of this exercise, the 1D functions have been excluded from the benchmarks.
The index of the test function is in SciPy Test Functions Index page: as the list is quite large, their definition has been split into multiple pages using the first letter of their name. Whenever possible, a 3D plot of the test function has been provided.
As an example, Figure 1.1 below contains some 3D representations of some of the benchmark functions in the SciPy Extended test suite.
Alpine 1 |
Corana |
Deceptive |
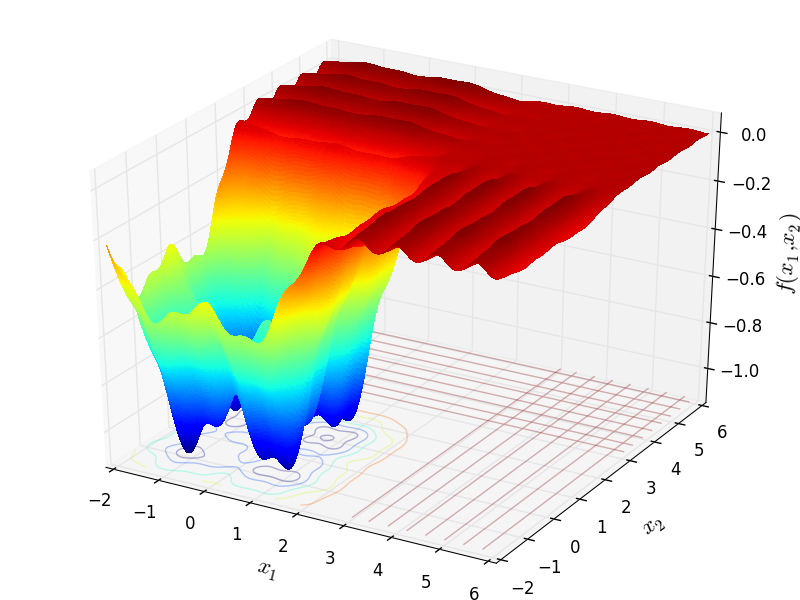
Gramacy Lee 3 |
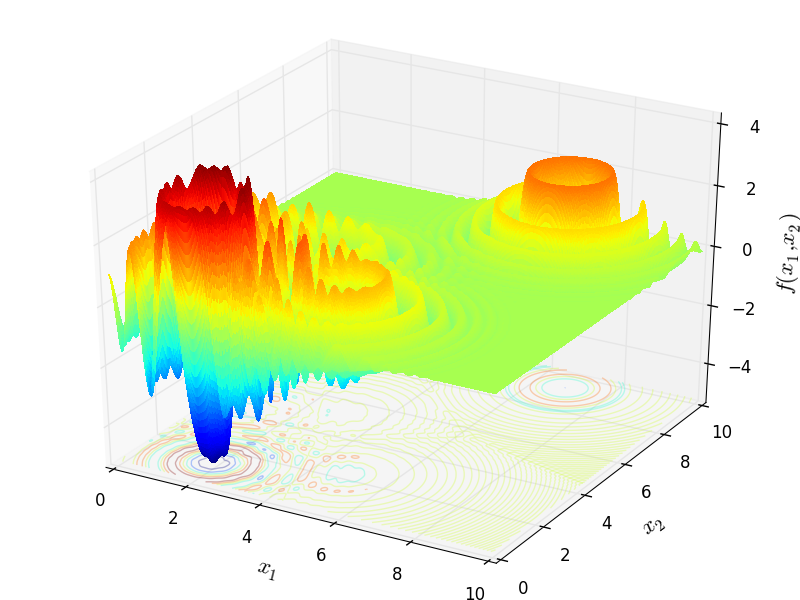
Langermann |
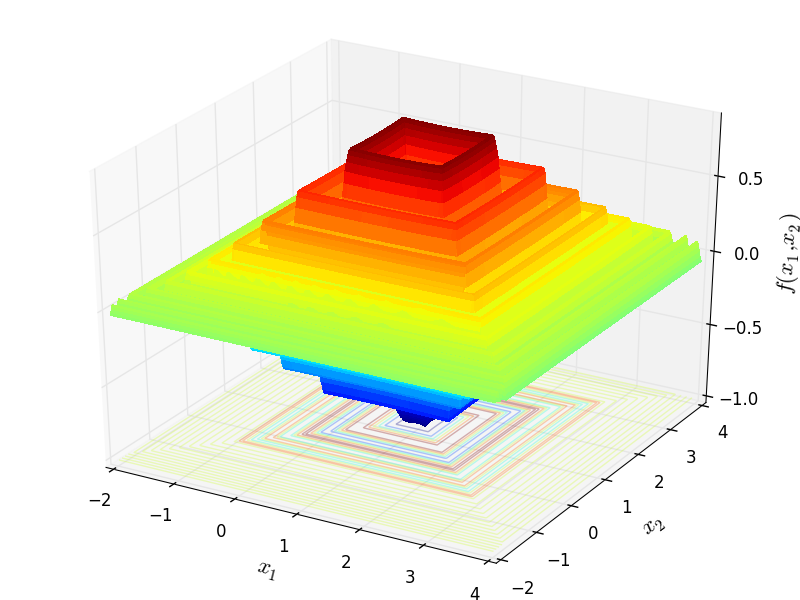
OddSquare |
Note
If you wish to contribute to the test suite (i.e., to add a new benchmark problem), please do send me an email to andrea.gavana@gmail.com, I’ll integrate your contribution with due credits and I will re-run the algorithms comparison.
 Methodology¶
Methodology¶Most of the classical test functions found in the literature suffer from a number of limitations and weaknesses, that are often exploited by global optimization algorithms:
For all these reasons, I now actually prefer test function generators to the standard, classical benchmarks, although the latter are so much more beautiful to look at :-) .
That said, one approach I have taken to break some of the issues above is to shift the global optimum of all functions to a new, random point inside the function domain. One possibility for doing that is kind-of explained in the paper Novel composition test functions for numerical global optimization, and it can be sketched as follow:
Start with the original function 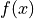 , and leave the original bounds untouched.
, and leave the original bounds untouched.
If we define 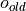 to be the original global optimum and
to be the original global optimum and 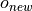 the new, randomly generated
global optimum, then we can define a new function as:
the new, randomly generated
global optimum, then we can define a new function as:
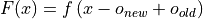
which we will then use as our optimization target function. Of course, by doing that we risk that some of the points passed by the optimizer to the new objective function will be translated outside the original domain: to avoid this, I have introduced a penalty function for when the evaluation point goes out of the specified bounds.
If we define:
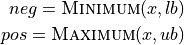
Then our penalty function 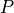 becomes:
becomes:
 General Solvers Performances¶
General Solvers Performances¶Table 1.1 below shows the overall success of all Global Optimization algorithms, considering for every benchmark function 100 random starting points,
for a maximum allowable budget of  .
.
As said in the introduction, quite a few solvers do not really support an initial starting point, but life is tough :-) .
Looking at the table, for example, BiteOpt comes out as the winner solving 83.4% of the problems using, on average, around 430 functions evaluations. MCS comes close second at 81.9% solved benchmarks but with a much lower budget at 235 functions evaluations.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 69.47% | 321 |
| BasinHopping | 64.68% | 314 |
| BiteOpt | 83.40% | 430 |
| CMA-ES | 58.78% | 570 |
| CRS2 | 73.41% | 806 |
| DE | 75.39% | 1,059 |
| DIRECT | 72.50% | 376 |
| DualAnnealing | 72.42% | 256 |
| LeapFrog | 61.85% | 314 |
| MCS | 81.95% | 235 |
| PSWARM | 21.19% | 1,420 |
| SCE | 71.16% | 522 |
| SHGO | 69.75% | 252 |
These results are also depicted in Figure 1.2, which shows that BiteOpt is the better-performing optimization algorithm, closely followed by MCS. Excluding PSWARM, all the solvers were able to reach the global optimum for at least 50% of the problems, on average.
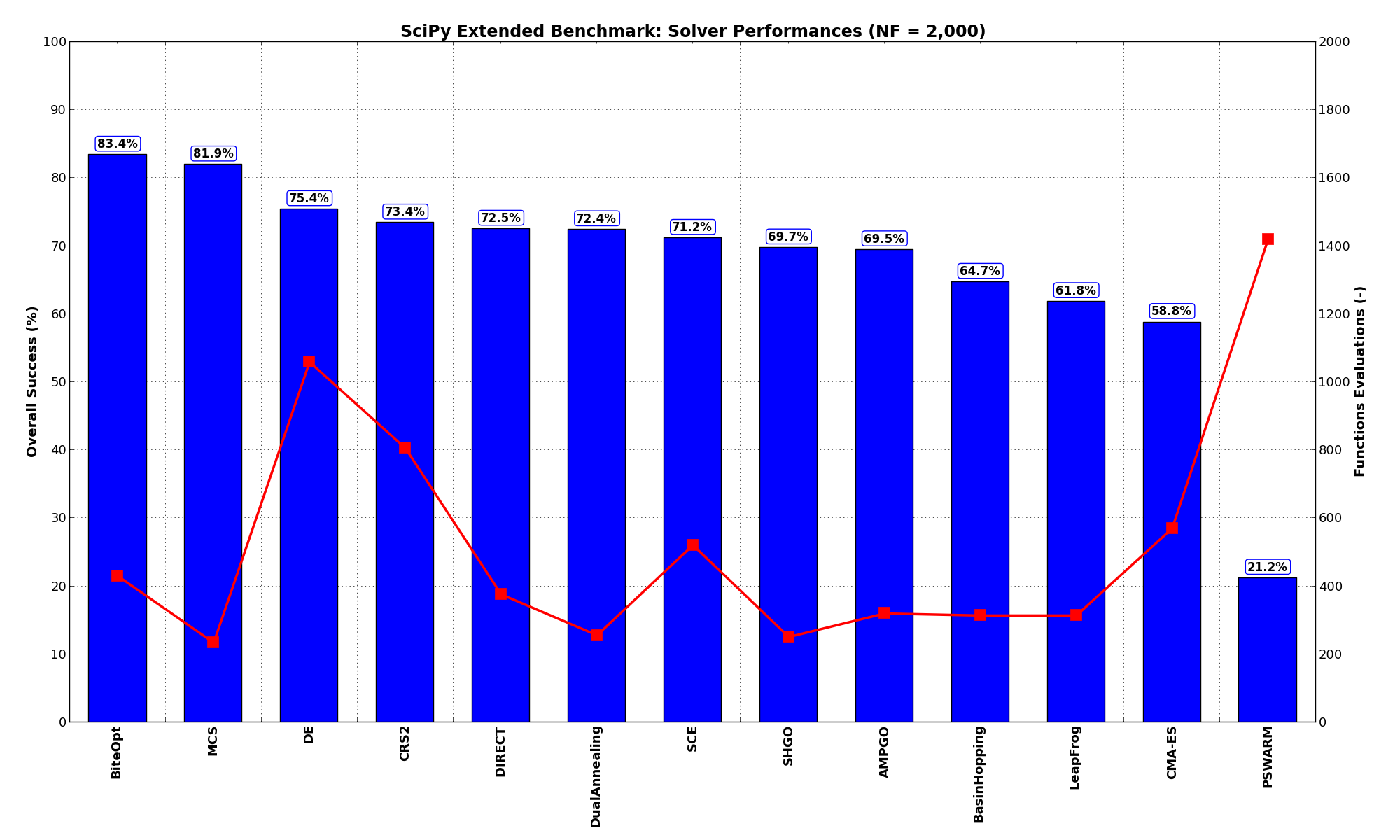
Figure 1.2: Optimization algorithms performances on the SciPy Extended test suite at 
Pushing the available budget to a very generous  , the results do not change that much in terms of
ranking between the two best solvers (BiteOpt and MCS), but there is a significant uptick in performances
for PSWARM and AMPGO, while a less pronounced one can be seen for SCE, as shown in Table 1.2 and
Figure 1.3.
, the results do not change that much in terms of
ranking between the two best solvers (BiteOpt and MCS), but there is a significant uptick in performances
for PSWARM and AMPGO, while a less pronounced one can be seen for SCE, as shown in Table 1.2 and
Figure 1.3.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 80.67% | 1,023 |
| BasinHopping | 69.32% | 553 |
| BiteOpt | 89.85% | 728 |
| CMA-ES | 61.76% | 696 |
| CRS2 | 79.76% | 1,035 |
| DE | 84.25% | 1,442 |
| DIRECT | 77.88% | 666 |
| DualAnnealing | 77.16% | 441 |
| LeapFrog | 62.70% | 361 |
| MCS | 88.68% | 578 |
| PSWARM | 75.93% | 2,626 |
| SCE | 79.97% | 958 |
| SHGO | 77.05% | 692 |
These results are also depicted in Figure 1.3, which shows the dramatic improvement of the PSWARM algorithm when given enough budget of functions evaluations - and this is also reflected on the average number of functions evaluations for solved problems (2,626). Similar, but less dramatic conclusions can be reached for AMPGO.
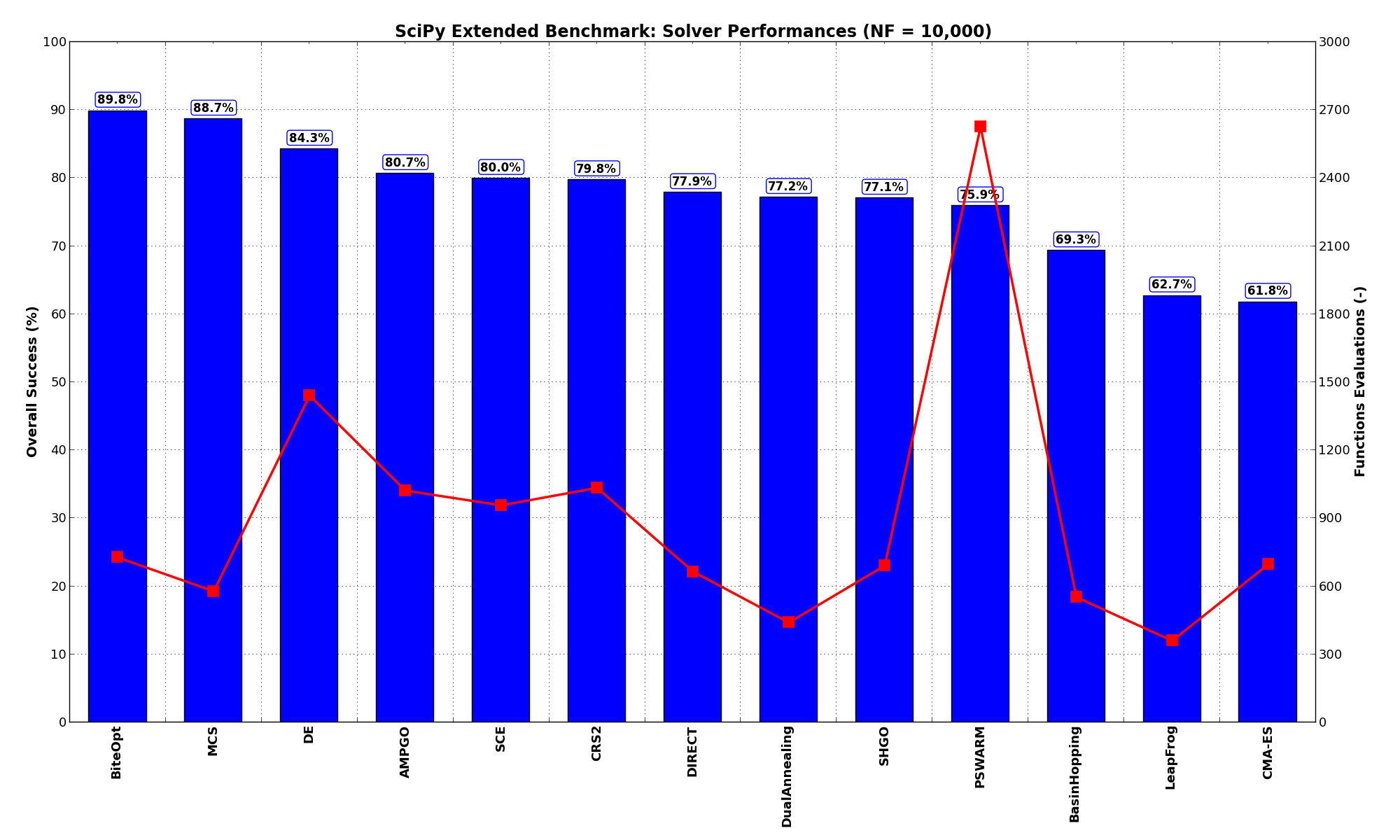
Figure 1.3: Optimization algorithms performances on the SciPy Extended test suite at 
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 1.4.
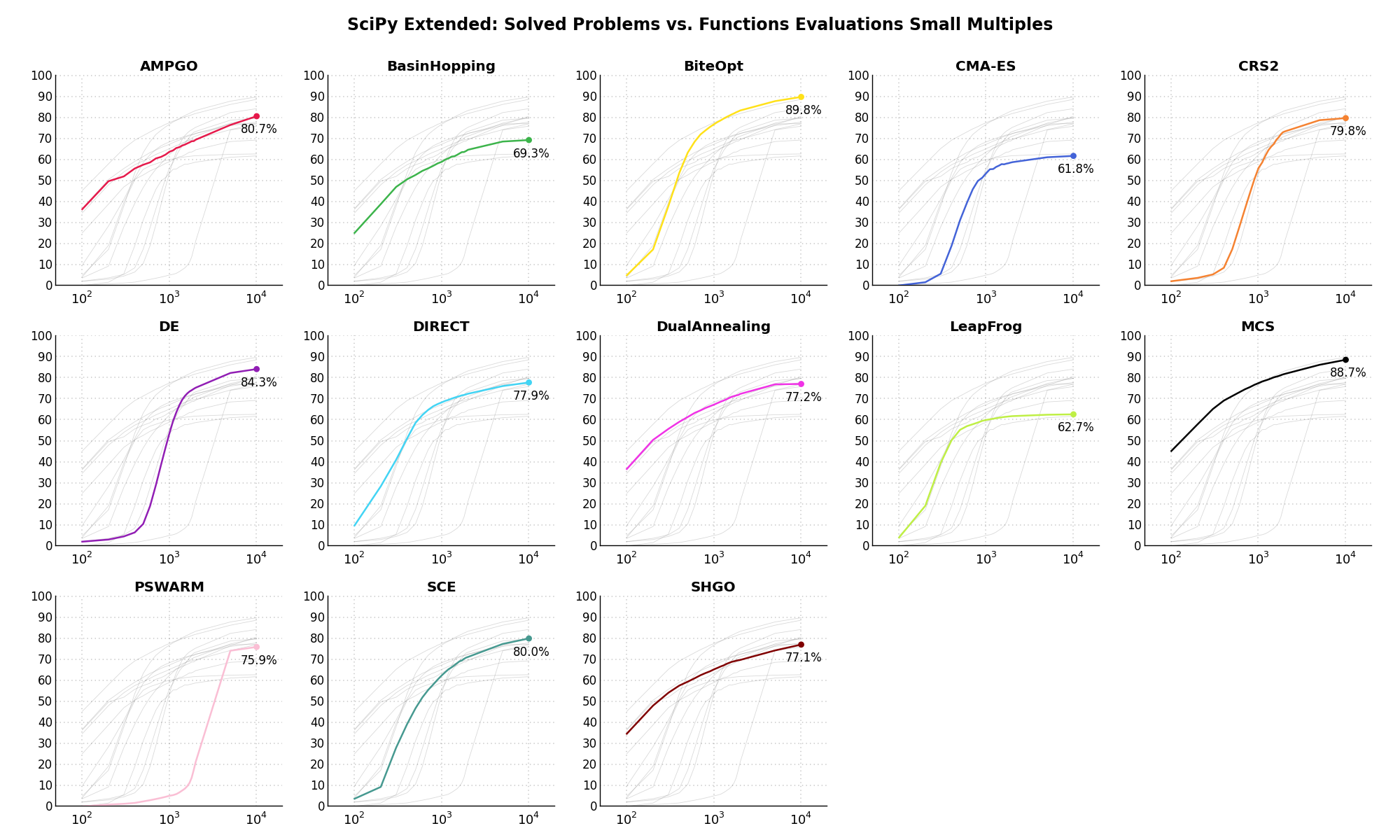
Figure 1.4: Percentage of problems solved given a fixed number of function evaluations on the SciPy Extended test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 1.5 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
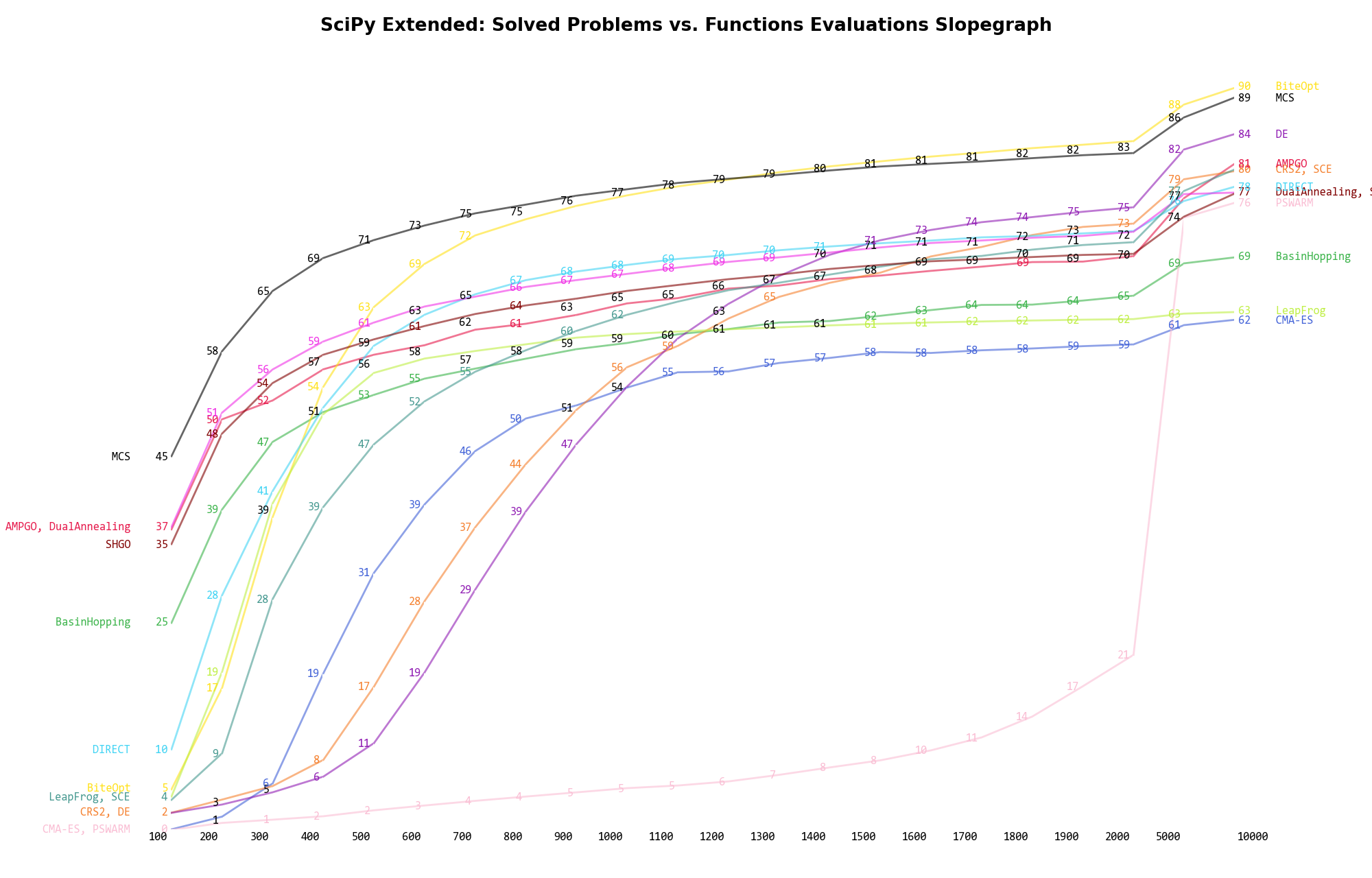
Figure 1.5: Percentage of problems solved given a fixed number of function evaluations on the SciPy Extended test suite
A few obvious conclusions we can draw from these pictures are:
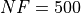 budget mark. In the end it surpasses also MCS at
around the
budget mark. In the end it surpasses also MCS at
around the 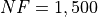 cutoff to claim the top spot to the end.
cutoff to claim the top spot to the end.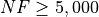 is phenomenal,
going from 20% to 70% solved benchmarks. A similar - but less squished - curve can be seen for DE,
which given enough function evaluations surpasses all the other SciPy solvers.
is phenomenal,
going from 20% to 70% solved benchmarks. A similar - but less squished - curve can be seen for DE,
which given enough function evaluations surpasses all the other SciPy solvers. Tolerance Sensitivities¶
Tolerance Sensitivities¶I admit that choosing a tolerance of 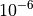 is kind of arbitrary per se, so I have decided to
repeat part of the SciPy Extended test suite with different tolerances, and specifically:
is kind of arbitrary per se, so I have decided to
repeat part of the SciPy Extended test suite with different tolerances, and specifically:
 .
.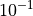 ,
, 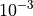 ,
, 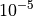 ,
, 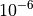 and
and  - the next to last I already had it.
- the next to last I already had it.I am not sure I was expecting any surprise here, but in any case Table 1.3 gives a summary of the solvers performances with a variable tolerance.
| Tolerance | AMPGO | BasinHopping | BiteOpt | CMA-ES | CRS2 | DE | DIRECT | DualAnnealing | LeapFrog | MCS | PSWARM | SCE | SHGO | Best Solver |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
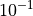 |
80.2% | 69.1% | 92.5% | 81.6% | 86.8% | 90.5% | 86.6% | 85.6% | 73.6% | 92.9% | 85.3% | 88.7% | 72.2% | MCS |
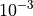 |
71.4% | 67.8% | 86.2% | 71.8% | 77.7% | 82.2% | 76.7% | 74.8% | 64.2% | 85.2% | 62.8% | 76.9% | 71.0% | BiteOpt |
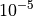 |
69.6% | 65.1% | 84.0% | 69.5% | 75.1% | 77.2% | 73.7% | 72.4% | 62.4% | 83.2% | 37.8% | 73.3% | 70.1% | BiteOpt |
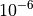 |
69.5% | 64.7% | 83.4% | 58.8% | 73.4% | 75.4% | 72.5% | 72.3% | 61.8% | 81.9% | 21.2% | 71.2% | 69.7% | BiteOpt |
 |
67.3% | 54.4% | 79.9% | 54.8% | 68.2% | 70.5% | 67.9% | 64.9% | 59.5% | 80.2% | 6.1% | 70.0% | 63.6% | MCS |
What we can see from the table is that the two top solvers in this specific benchmark suite keep their crown and stay well above all the other optimization algorithms. In general it is to be expected that by tightening the tolerance less problems will be solved, however some of the algorithms show a much steeper decrease in performances compared to others.
For example, BiteOpt and MCS lose about 12% of the benchmarks when
the tolerance goes from 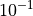 to
to  , while DE, DIRECT and DualAnnealing are
closer to 20% and PSWARM has a dramatic drop of 80%.
, while DE, DIRECT and DualAnnealing are
closer to 20% and PSWARM has a dramatic drop of 80%.
The results from Table 1.3 are visualized in Figure 1.6 below.
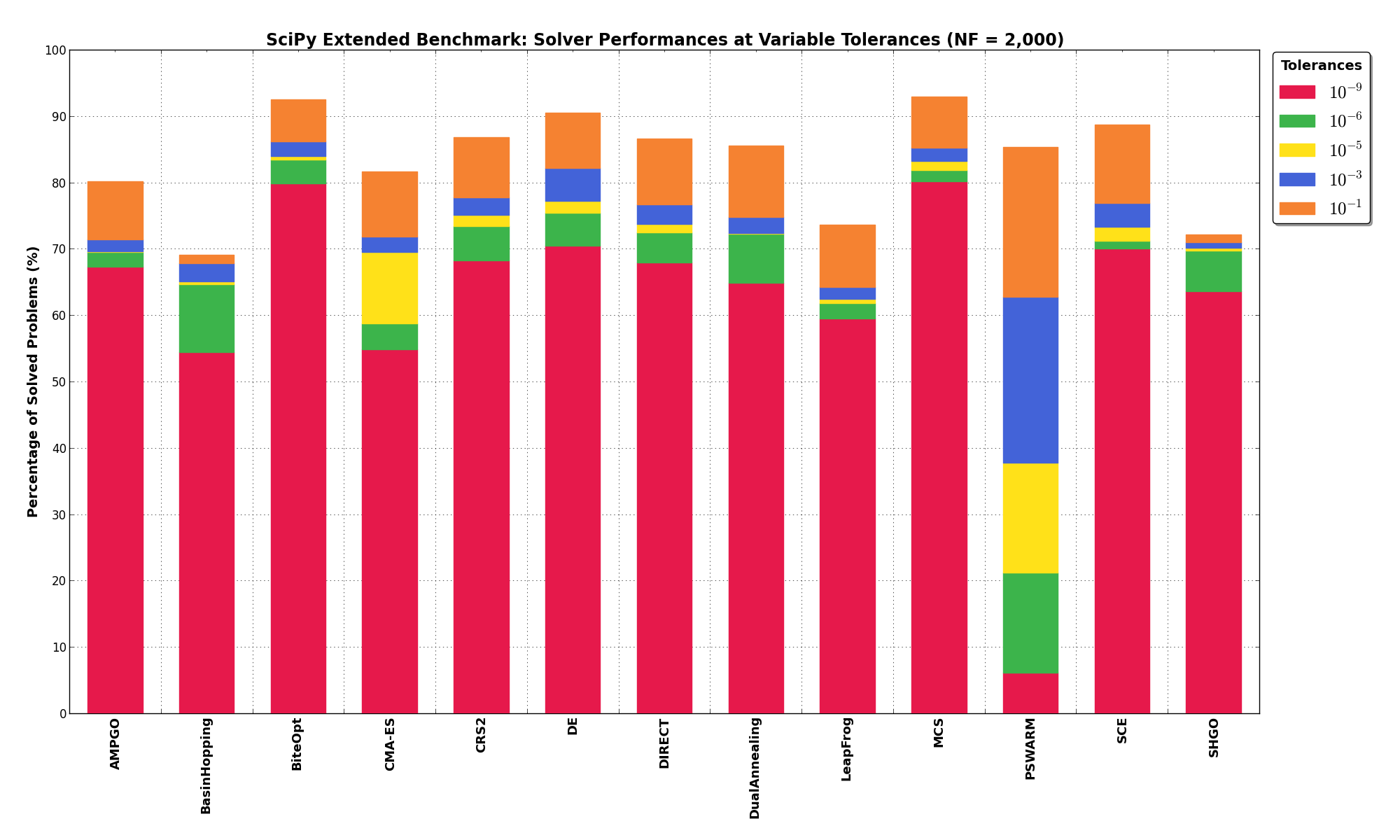
Figure 1.6: Percentage of problems solved as a function of tolerance on the SciPy Extended test suite
From the picture above it is even more striking to see the drop of PSWARM.
 Tough Functions and Boring Tables¶
Tough Functions and Boring Tables¶As I did in the previous benchmark, I will dedicate a section to the “toughest” functions in this benchmark suite. The test suite contains a variety of Global Optimization problems, some of them are harder to solve than others, irrespectively of the algorithm chosen to minimize the test function.
Table 1.4 has been obtained by running all the Global Optimizers available against all the N-D test
functions for a collection of 100 random starting points with a maximum budget of  ,
and then averaging the successful minimizations across all the optimizers.
,
and then averaging the successful minimizations across all the optimizers.
| Test Function | N | Overall Success (%) |
|---|---|---|
| HappyCat | 2 | 0.15% |
| Bukin06 | 2 | 0.31% |
| Cola | 17 | 1.00% |
| CrownedCross | 2 | 7.31% |
| CrossLegTable | 2 | 7.54% |
| Meyer | 3 | 8.23% |
| Paviani | 10 | 9.77% |
| Thurber | 7 | 9.85% |
| SineEnvelope | 2 | 13.31% |
| Peaks | 2 | 14.69% |
| Trefethen | 2 | 14.77% |
| Whitley | 2 | 14.92% |
| NewFunction02 | 2 | 15.38% |
| Mishra04 | 2 | 15.38% |
| Mishra03 | 2 | 15.38% |
| DeVilliersGlasser02 | 5 | 15.38% |
| BiggsExp06 | 6 | 15.62% |
| Zagros | 2 | 18.00% |
| Xor | 9 | 23.08% |
| EggHolder | 2 | 23.08% |
| BiggsExp05 | 5 | 26.15% |
| Zimmerman | 2 | 28.62% |
| XinSheYang03 | 2 | 30.15% |
| NewFunction01 | 2 | 30.77% |
| Rana | 2 | 30.77% |
| Osborne | 5 | 30.77% |
| Salomon | 2 | 31.69% |
| PowerSum | 4 | 31.92% |
| Griewank | 2 | 33.62% |
| Damavandi | 2 | 33.62% |
| Ripple01 | 2 | 34.38% |
| Stochastic | 2 | 36.38% |
| Kowalik | 4 | 41.46% |
| Hougen | 5 | 42.23% |
| Schaffer01 | 2 | 43.38% |
| Schaffer04 | 2 | 46.00% |
| XinSheYang01 | 2 | 47.69% |
| Ackley04 | 2 | 48.85% |
| Schaffer03 | 2 | 51.54% |
| Schaffer02 | 2 | 51.69% |
| Watson | 6 | 53.54% |
| Deceptive | 2 | 53.69% |
| UrsemWaves | 2 | 53.85% |
| DropWave | 2 | 54.23% |
| ZeroSum | 2 | 54.85% |
| Spike | 2 | 55.23% |
| OddSquare | 2 | 55.54% |
| RosenbrockModified | 2 | 57.69% |
| MeyerRoth | 3 | 58.85% |
| Corana | 4 | 59.15% |
| Colville | 4 | 59.31% |
| Weierstrass | 2 | 60.69% |
| Ratkowsky01 | 4 | 60.92% |
| Easom | 2 | 61.00% |
| DeVilliersGlasser01 | 4 | 61.54% |
| Simpleton | 10 | 61.54% |
| XinSheYang04 | 2 | 63.46% |
| Gulf | 3 | 63.69% |
| Price02 | 2 | 64.69% |
| Shekel10 | 4 | 65.08% |
| AMGM | 2 | 65.54% |
| InvertedCosine | 2 | 65.69% |
| TestTubeHolder | 2 | 66.15% |
| Eckerle4 | 3 | 67.08% |
| DeJong5 | 2 | 67.46% |
| MultiGaussian | 2 | 67.85% |
| DeflectedCorrugatedSpring | 2 | 68.77% |
| Shekel07 | 4 | 69.08% |
| Shekel05 | 4 | 69.92% |
| Ackley01 | 2 | 70.00% |
| Price03 | 2 | 70.77% |
| Chichinadze | 2 | 71.15% |
| Levy05 | 2 | 71.92% |
| Penalty02 | 2 | 72.23% |
| Crescent | 2 | 72.62% |
| Tripod | 2 | 73.31% |
| BiggsExp04 | 4 | 73.85% |
| GramacyLee03 | 2 | 74.38% |
| Shubert03 | 2 | 75.38% |
| Wavy | 2 | 75.46% |
| Ursem03 | 2 | 75.69% |
| Dolan | 5 | 75.77% |
| XinSheYang02 | 2 | 76.00% |
| Pathological | 2 | 76.15% |
| Rastrigin | 2 | 76.69% |
| Alpine02 | 2 | 76.85% |
| SchmidtVetters | 3 | 76.92% |
| Mishra05 | 2 | 76.92% |
| CarromTable | 2 | 76.92% |
| Hansen | 2 | 78.00% |
| Branin02 | 2 | 79.08% |
| BuecheRastrigin | 2 | 79.08% |
| Ripple25 | 2 | 79.08% |
| Mishra06 | 2 | 79.08% |
| YaoLiu09 | 2 | 79.54% |
| Schwefel26 | 2 | 79.54% |
| Trid | 6 | 80.08% |
| LunacekBiRastrigin | 2 | 80.77% |
| Powell | 4 | 81.46% |
| Tsoulos | 2 | 82.69% |
| Mishra10 | 2 | 82.77% |
| VenterSobiezcczanskiSobieski | 2 | 82.85% |
| Trigonometric02 | 2 | 82.92% |
| Sinusoidal | 2 | 82.92% |
| SphericalSinc | 2 | 83.00% |
| Gear | 4 | 83.00% |
| Shubert01 | 2 | 83.69% |
| Deb03 | 2 | 83.69% |
| Shubert04 | 2 | 84.23% |
| F2 | 2 | 84.46% |
| HolderTable01 | 2 | 84.46% |
| HolderTable02 | 2 | 84.62% |
| Schwefel36 | 2 | 84.62% |
| PenHolder | 2 | 84.62% |
| GramacyLee02 | 2 | 84.62% |
| FreudensteinRoth | 2 | 85.85% |
| CrossInTray | 2 | 86.46% |
| Plateau | 2 | 86.77% |
| Step01 | 2 | 86.85% |
| Quintic | 2 | 87.08% |
| ElAttarVidyasagarDutta | 2 | 87.08% |
| Step02 | 2 | 87.23% |
| Langermann | 2 | 87.31% |
| Schwefel06 | 2 | 87.69% |
| Pinter | 2 | 88.00% |
| Vincent | 2 | 88.23% |
| EggCrate | 2 | 88.46% |
| Step03 | 2 | 89.00% |
| Bird | 2 | 90.00% |
| Penalty01 | 2 | 90.69% |
| Mishra09 | 3 | 90.85% |
| Deb01 | 2 | 90.92% |
| StyblinskiTang | 2 | 91.15% |
| Trigonometric01 | 2 | 91.38% |
| Schwefel21 | 2 | 91.85% |
| Hartmann6 | 6 | 92.00% |
| Schwefel22 | 2 | 92.15% |
| Schwefel20 | 2 | 92.23% |
| MieleCantrell | 4 | 92.31% |
| RosenbrockDisc | 2 | 92.31% |
| LennardJones | 6 | 92.31% |
| Friedman | 5 | 92.31% |
| Ackley02 | 2 | 92.54% |
| YaoLiu04 | 2 | 92.62% |
| Alpine01 | 2 | 92.85% |
| Levy13 | 2 | 93.08% |
| Ursem04 | 2 | 93.08% |
| Ackley03 | 2 | 93.15% |
| SawtoothXY | 2 | 93.31% |
| Ratkowsky02 | 3 | 93.31% |
| DeckkersAarts | 2 | 93.54% |
| HelicalValley | 3 | 93.62% |
| Engvall | 2 | 93.77% |
| BoxBetts | 3 | 94.15% |
| Bohachevsky02 | 2 | 94.23% |
| Michalewicz | 2 | 94.23% |
| HyperGrid | 2 | 94.69% |
| Bohachevsky01 | 2 | 95.00% |
| Decanomial | 2 | 95.38% |
| BartelsConn | 2 | 95.46% |
| MullerBrown | 2 | 95.54% |
| Mishra08 | 2 | 95.54% |
| ThreeHumpCamel | 2 | 95.54% |
| HimmelBlau | 2 | 95.69% |
| Parsopoulos | 2 | 95.69% |
| GoldsteinPrice | 2 | 96.15% |
| Ursem01 | 2 | 96.23% |
| SixHumpCamel | 2 | 96.38% |
| Levy03 | 2 | 96.46% |
| Cigar | 2 | 96.54% |
| Branin01 | 2 | 96.62% |
| Beale | 2 | 96.69% |
| Judge | 2 | 96.77% |
| Price04 | 2 | 96.85% |
| Zirilli | 2 | 96.92% |
| StretchedV | 2 | 97.00% |
| Picheny | 2 | 97.08% |
| Bohachevsky03 | 2 | 97.15% |
| Hartmann3 | 3 | 97.23% |
| PermFunction01 | 2 | 97.54% |
| WayburnSeader01 | 2 | 97.54% |
| BiggsExp03 | 3 | 97.62% |
| Leon | 2 | 97.62% |
| Price01 | 2 | 97.77% |
| McCormick | 2 | 97.85% |
| Cube | 2 | 97.85% |
| Kearfott | 2 | 98.00% |
| Qing | 2 | 98.08% |
| WayburnSeader02 | 2 | 98.38% |
| Bukin04 | 2 | 98.38% |
| Giunta | 2 | 98.46% |
| Rosenbrock | 2 | 98.46% |
| BiggsExp02 | 2 | 98.46% |
| Exp2 | 2 | 98.54% |
| ReduxSum | 2 | 98.62% |
| Mishra11 | 2 | 98.62% |
| Mishra10b | 2 | 98.69% |
| WayburnSeader03 | 2 | 98.85% |
| Brent | 2 | 98.92% |
| Treccani | 2 | 98.92% |
| PermFunction02 | 2 | 99.00% |
| JennrichSampson | 2 | 99.08% |
| RotatedEllipse01 | 2 | 99.08% |
| Schwefel04 | 2 | 99.15% |
| RotatedEllipse02 | 2 | 99.23% |
| NeedleEye | 2 | 99.23% |
| DixonPrice | 2 | 99.31% |
| Mishra07 | 2 | 99.46% |
| LunacekBiSphere | 2 | 99.46% |
| Zettl | 2 | 99.54% |
| TridiagonalMatrix | 2 | 99.54% |
| Exponential | 2 | 99.62% |
| Keane | 2 | 99.77% |
| Schwefel01 | 2 | 99.77% |
| Sargan | 2 | 99.77% |
| Matyas | 2 | 99.77% |
| Brown | 2 | 99.85% |
| Zacharov | 2 | 99.85% |
| Quadratic | 2 | 99.85% |
| Sodp | 2 | 99.85% |
| Sphere | 2 | 99.85% |
| Schwefel02 | 2 | 99.92% |
| MultiModal | 2 | 99.92% |
| Csendes | 2 | 99.92% |
| Bukin02 | 2 | 100.00% |
| Hosaki | 2 | 100.00% |
| Brad | 3 | 100.00% |
| Booth | 2 | 100.00% |
| CosineMixture | 2 | 100.00% |
| Mishra02 | 2 | 100.00% |
| Mishra01 | 2 | 100.00% |
| Adjiman | 2 | 100.00% |
| Katsuura | 2 | 100.00% |
| Wolfe | 3 | 100.00% |
| Infinity | 2 | 100.00% |
It can be easily seen that the HappyCat, Bukin06 and Cola were always hard problems for all the algorithms, while others like Bukin02 and CosineMixture are amongst the easiest ones.
Table 1.5 is a split-by-benchmark function of the first table, showing the percentage of successful
optimizations per benchmark with a maximum budget of 
| Test Function | N | AMPGO | BasinHopping | BiteOpt | CMA-ES | CRS2 | DE | DIRECT | DualAnnealing | LeapFrog | MCS | PSWARM | SCE | SHGO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ackley01 | 2 | 90.0 | 98.0 | 100.0 | 15.0 | 84.0 | 95.0 | 38.0 | 99.0 | 14.0 | 87.0 | 88.0 | 96.0 | 6.0 |
| Ackley02 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 95.0 | 100.0 | 100.0 | 51.0 | 100.0 | 100.0 | 95.0 | 100.0 | 62.0 |
| Ackley03 | 2 | 100.0 | 97.0 | 100.0 | 39.0 | 98.0 | 100.0 | 100.0 | 98.0 | 82.0 | 100.0 | 98.0 | 99.0 | 100.0 |
| Ackley04 | 2 | 100.0 | 23.0 | 43.0 | 31.0 | 45.0 | 23.0 | 95.0 | 50.0 | 15.0 | 79.0 | 17.0 | 14.0 | 100.0 |
| Adjiman | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Alpine01 | 2 | 100.0 | 92.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 | 32.0 | 100.0 | 100.0 | 100.0 | 85.0 | 100.0 |
| Alpine02 | 2 | 100.0 | 37.0 | 96.0 | 48.0 | 40.0 | 45.0 | 84.0 | 81.0 | 71.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| AMGM | 2 | 100.0 | 54.0 | 100.0 | 44.0 | 14.0 | 1.0 | 45.0 | 53.0 | 42.0 | 100.0 | 100.0 | 99.0 | 100.0 |
| BartelsConn | 2 | 99.0 | 100.0 | 100.0 | 88.0 | 100.0 | 100.0 | 85.0 | 93.0 | 100.0 | 79.0 | 97.0 | 100.0 | 100.0 |
| Beale | 2 | 100.0 | 100.0 | 98.0 | 83.0 | 97.0 | 100.0 | 100.0 | 98.0 | 84.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| BiggsExp02 | 2 | 100.0 | 99.0 | 100.0 | 99.0 | 96.0 | 100.0 | 100.0 | 100.0 | 99.0 | 88.0 | 99.0 | 100.0 | 100.0 |
| BiggsExp03 | 3 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 96.0 | 100.0 | 91.0 | 98.0 | 85.0 | 100.0 | 100.0 |
| BiggsExp04 | 4 | 61.0 | 95.0 | 100.0 | 100.0 | 98.0 | 100.0 | 3.0 | 91.0 | 62.0 | 94.0 | 2.0 | 100.0 | 54.0 |
| BiggsExp05 | 5 | 28.0 | 24.0 | 60.0 | 55.0 | 40.0 | 35.0 | 0.0 | 4.0 | 2.0 | 60.0 | 0.0 | 28.0 | 4.0 |
| BiggsExp06 | 6 | 14.0 | 12.0 | 56.0 | 30.0 | 43.0 | 0.0 | 0.0 | 3.0 | 0.0 | 40.0 | 0.0 | 4.0 | 1.0 |
| Bird | 2 | 100.0 | 56.0 | 98.0 | 69.0 | 88.0 | 92.0 | 100.0 | 99.0 | 74.0 | 99.0 | 96.0 | 99.0 | 100.0 |
| Bohachevsky01 | 2 | 100.0 | 100.0 | 100.0 | 82.0 | 98.0 | 100.0 | 100.0 | 100.0 | 85.0 | 86.0 | 100.0 | 100.0 | 84.0 |
| Bohachevsky02 | 2 | 100.0 | 100.0 | 98.0 | 92.0 | 98.0 | 100.0 | 100.0 | 98.0 | 65.0 | 84.0 | 98.0 | 100.0 | 92.0 |
| Bohachevsky03 | 2 | 100.0 | 100.0 | 100.0 | 91.0 | 99.0 | 100.0 | 100.0 | 100.0 | 90.0 | 90.0 | 99.0 | 100.0 | 94.0 |
| Booth | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| BoxBetts | 3 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 84.0 | 91.0 | 100.0 | 94.0 | 100.0 | 56.0 |
| Brad | 3 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Branin01 | 2 | 100.0 | 88.0 | 97.0 | 91.0 | 91.0 | 99.0 | 100.0 | 99.0 | 93.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| Branin02 | 2 | 99.0 | 58.0 | 83.0 | 51.0 | 64.0 | 75.0 | 100.0 | 94.0 | 35.0 | 99.0 | 79.0 | 91.0 | 100.0 |
| Brent | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 92.0 | 95.0 | 100.0 | 100.0 |
| Brown | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| BuecheRastrigin | 2 | 52.0 | 81.0 | 100.0 | 5.0 | 84.0 | 92.0 | 100.0 | 100.0 | 24.0 | 99.0 | 91.0 | 100.0 | 100.0 |
| Bukin02 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Bukin04 | 2 | 99.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 87.0 | 100.0 | 97.0 | 98.0 | 100.0 | 100.0 |
| Bukin06 | 2 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| CarromTable | 2 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 |
| Chichinadze | 2 | 96.0 | 22.0 | 100.0 | 18.0 | 72.0 | 99.0 | 84.0 | 99.0 | 31.0 | 100.0 | 56.0 | 81.0 | 67.0 |
| Cigar | 2 | 95.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 88.0 | 100.0 | 72.0 |
| Cola | 17 | 1.0 | 1.0 | 0.0 | 10.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| Colville | 4 | 28.0 | 70.0 | 97.0 | 51.0 | 67.0 | 80.0 | 1.0 | 97.0 | 48.0 | 99.0 | 1.0 | 58.0 | 74.0 |
| Corana | 4 | 54.0 | 63.0 | 100.0 | 11.0 | 85.0 | 100.0 | 21.0 | 100.0 | 2.0 | 94.0 | 53.0 | 85.0 | 1.0 |
| CosineMixture | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Crescent | 2 | 100.0 | 20.0 | 100.0 | 98.0 | 91.0 | 100.0 | 17.0 | 6.0 | 100.0 | 63.0 | 92.0 | 100.0 | 57.0 |
| CrossInTray | 2 | 99.0 | 19.0 | 100.0 | 36.0 | 93.0 | 100.0 | 100.0 | 100.0 | 88.0 | 100.0 | 96.0 | 93.0 | 100.0 |
| CrossLegTable | 2 | 2.0 | 0.0 | 13.0 | 6.0 | 13.0 | 5.0 | 20.0 | 0.0 | 30.0 | 9.0 | 0.0 | 0.0 | 0.0 |
| CrownedCross | 2 | 6.0 | 0.0 | 19.0 | 5.0 | 11.0 | 7.0 | 7.0 | 0.0 | 17.0 | 22.0 | 1.0 | 0.0 | 0.0 |
| Csendes | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Cube | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 91.0 | 100.0 | 100.0 | 100.0 | 81.0 | 100.0 | 100.0 |
| Damavandi | 2 | 31.0 | 3.0 | 34.0 | 3.0 | 9.0 | 18.0 | 55.0 | 31.0 | 6.0 | 98.0 | 16.0 | 33.0 | 100.0 |
| Deb01 | 2 | 100.0 | 100.0 | 100.0 | 96.0 | 84.0 | 100.0 | 100.0 | 100.0 | 96.0 | 100.0 | 93.0 | 13.0 | 100.0 |
| Deb03 | 2 | 100.0 | 81.0 | 100.0 | 75.0 | 52.0 | 59.0 | 87.0 | 92.0 | 72.0 | 100.0 | 93.0 | 77.0 | 100.0 |
| Decanomial | 2 | 98.0 | 100.0 | 100.0 | 91.0 | 92.0 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 61.0 | 100.0 | 100.0 |
| Deceptive | 2 | 77.0 | 27.0 | 100.0 | 21.0 | 38.0 | 78.0 | 77.0 | 18.0 | 27.0 | 93.0 | 76.0 | 58.0 | 8.0 |
| DeckkersAarts | 2 | 99.0 | 79.0 | 100.0 | 93.0 | 89.0 | 100.0 | 100.0 | 78.0 | 85.0 | 95.0 | 98.0 | 100.0 | 100.0 |
| DeflectedCorrugatedSpring | 2 | 59.0 | 100.0 | 69.0 | 1.0 | 21.0 | 59.0 | 100.0 | 83.0 | 5.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| DeJong5 | 2 | 81.0 | 7.0 | 100.0 | 14.0 | 66.0 | 83.0 | 100.0 | 100.0 | 12.0 | 95.0 | 41.0 | 98.0 | 80.0 |
| DeVilliersGlasser01 | 4 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 |
| DeVilliersGlasser02 | 5 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| DixonPrice | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 95.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Dolan | 5 | 100.0 | 100.0 | 100.0 | 100.0 | 2.0 | 0.0 | 100.0 | 99.0 | 100.0 | 100.0 | 84.0 | 0.0 | 100.0 |
| DropWave | 2 | 17.0 | 100.0 | 57.0 | 3.0 | 35.0 | 55.0 | 24.0 | 56.0 | 10.0 | 97.0 | 93.0 | 71.0 | 87.0 |
| Easom | 2 | 60.0 | 0.0 | 100.0 | 1.0 | 95.0 | 100.0 | 17.0 | 60.0 | 50.0 | 100.0 | 15.0 | 95.0 | 100.0 |
| Eckerle4 | 3 | 100.0 | 25.0 | 100.0 | 11.0 | 94.0 | 99.0 | 2.0 | 99.0 | 41.0 | 92.0 | 55.0 | 96.0 | 58.0 |
| EggCrate | 2 | 100.0 | 59.0 | 100.0 | 34.0 | 98.0 | 99.0 | 100.0 | 100.0 | 63.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| EggHolder | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 |
| ElAttarVidyasagarDutta | 2 | 100.0 | 58.0 | 100.0 | 51.0 | 87.0 | 91.0 | 100.0 | 100.0 | 63.0 | 96.0 | 97.0 | 100.0 | 89.0 |
| Engvall | 2 | 100.0 | 100.0 | 100.0 | 19.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Exp2 | 2 | 100.0 | 99.0 | 100.0 | 100.0 | 91.0 | 100.0 | 100.0 | 100.0 | 99.0 | 92.0 | 100.0 | 100.0 | 100.0 |
| Exponential | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| F2 | 2 | 94.0 | 90.0 | 100.0 | 31.0 | 79.0 | 95.0 | 100.0 | 100.0 | 24.0 | 99.0 | 86.0 | 100.0 | 100.0 |
| FreudensteinRoth | 2 | 99.0 | 52.0 | 99.0 | 55.0 | 87.0 | 89.0 | 100.0 | 100.0 | 52.0 | 87.0 | 98.0 | 98.0 | 100.0 |
| Friedman | 5 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Gear | 4 | 100.0 | 3.0 | 100.0 | 99.0 | 99.0 | 100.0 | 100.0 | 100.0 | 61.0 | 100.0 | 100.0 | 100.0 | 17.0 |
| Giunta | 2 | 100.0 | 100.0 | 100.0 | 88.0 | 96.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 96.0 | 100.0 | 100.0 |
| GoldsteinPrice | 2 | 100.0 | 99.0 | 96.0 | 82.0 | 90.0 | 100.0 | 100.0 | 100.0 | 86.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| GramacyLee02 | 2 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| GramacyLee03 | 2 | 100.0 | 49.0 | 100.0 | 33.0 | 56.0 | 54.0 | 100.0 | 100.0 | 27.0 | 96.0 | 68.0 | 84.0 | 100.0 |
| Griewank | 2 | 53.0 | 0.0 | 50.0 | 2.0 | 62.0 | 47.0 | 17.0 | 46.0 | 5.0 | 93.0 | 38.0 | 3.0 | 21.0 |
| Gulf | 3 | 95.0 | 40.0 | 100.0 | 70.0 | 90.0 | 100.0 | 0.0 | 43.0 | 82.0 | 93.0 | 0.0 | 100.0 | 15.0 |
| Hansen | 2 | 82.0 | 94.0 | 91.0 | 20.0 | 67.0 | 95.0 | 75.0 | 92.0 | 31.0 | 100.0 | 89.0 | 78.0 | 100.0 |
| HappyCat | 2 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Hartmann3 | 3 | 100.0 | 100.0 | 98.0 | 98.0 | 97.0 | 100.0 | 100.0 | 97.0 | 81.0 | 100.0 | 93.0 | 100.0 | 100.0 |
| Hartmann6 | 6 | 100.0 | 100.0 | 93.0 | 94.0 | 96.0 | 97.0 | 94.0 | 93.0 | 75.0 | 95.0 | 67.0 | 99.0 | 93.0 |
| HelicalValley | 3 | 83.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 94.0 | 100.0 | 96.0 | 98.0 | 46.0 | 100.0 | 100.0 |
| HimmelBlau | 2 | 100.0 | 74.0 | 99.0 | 91.0 | 91.0 | 100.0 | 100.0 | 100.0 | 91.0 | 100.0 | 99.0 | 99.0 | 100.0 |
| HolderTable01 | 2 | 100.0 | 37.0 | 100.0 | 36.0 | 87.0 | 98.0 | 97.0 | 100.0 | 47.0 | 100.0 | 96.0 | 100.0 | 100.0 |
| HolderTable02 | 2 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 |
| Hosaki | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Hougen | 5 | 9.0 | 69.0 | 98.0 | 71.0 | 95.0 | 22.0 | 0.0 | 16.0 | 0.0 | 68.0 | 0.0 | 64.0 | 37.0 |
| HyperGrid | 2 | 100.0 | 100.0 | 100.0 | 89.0 | 90.0 | 100.0 | 100.0 | 100.0 | 93.0 | 100.0 | 96.0 | 63.0 | 100.0 |
| Infinity | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| InvertedCosine | 2 | 35.0 | 42.0 | 70.0 | 3.0 | 50.0 | 78.0 | 73.0 | 98.0 | 10.0 | 95.0 | 100.0 | 100.0 | 100.0 |
| JennrichSampson | 2 | 99.0 | 97.0 | 100.0 | 100.0 | 95.0 | 100.0 | 100.0 | 98.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Judge | 2 | 100.0 | 98.0 | 95.0 | 87.0 | 96.0 | 99.0 | 100.0 | 98.0 | 86.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Katsuura | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Keane | 2 | 100.0 | 100.0 | 100.0 | 99.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Kearfott | 2 | 100.0 | 94.0 | 100.0 | 99.0 | 93.0 | 100.0 | 100.0 | 100.0 | 91.0 | 99.0 | 99.0 | 99.0 | 100.0 |
| Kowalik | 4 | 42.0 | 35.0 | 62.0 | 41.0 | 77.0 | 79.0 | 0.0 | 12.0 | 33.0 | 72.0 | 1.0 | 73.0 | 12.0 |
| Langermann | 2 | 85.0 | 92.0 | 98.0 | 32.0 | 86.0 | 98.0 | 100.0 | 100.0 | 47.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| LennardJones | 6 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 |
| Leon | 2 | 100.0 | 99.0 | 100.0 | 96.0 | 100.0 | 99.0 | 100.0 | 90.0 | 95.0 | 99.0 | 91.0 | 100.0 | 100.0 |
| Levy03 | 2 | 100.0 | 77.0 | 100.0 | 87.0 | 99.0 | 100.0 | 100.0 | 100.0 | 92.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Levy05 | 2 | 77.0 | 76.0 | 90.0 | 23.0 | 51.0 | 80.0 | 77.0 | 79.0 | 19.0 | 100.0 | 69.0 | 95.0 | 99.0 |
| Levy13 | 2 | 99.0 | 100.0 | 100.0 | 61.0 | 91.0 | 100.0 | 100.0 | 99.0 | 74.0 | 99.0 | 97.0 | 100.0 | 90.0 |
| LunacekBiRastrigin | 2 | 69.0 | 85.0 | 100.0 | 9.0 | 81.0 | 90.0 | 100.0 | 100.0 | 18.0 | 99.0 | 99.0 | 100.0 | 100.0 |
| LunacekBiSphere | 2 | 100.0 | 96.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| Matyas | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 99.0 |
| McCormick | 2 | 100.0 | 82.0 | 100.0 | 95.0 | 98.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| Meyer | 3 | 0.0 | 0.0 | 37.0 | 0.0 | 12.0 | 12.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 46.0 | 0.0 |
| MeyerRoth | 3 | 72.0 | 47.0 | 79.0 | 56.0 | 84.0 | 90.0 | 3.0 | 36.0 | 63.0 | 97.0 | 43.0 | 94.0 | 1.0 |
| Michalewicz | 2 | 99.0 | 100.0 | 100.0 | 63.0 | 88.0 | 100.0 | 100.0 | 100.0 | 77.0 | 100.0 | 99.0 | 99.0 | 100.0 |
| MieleCantrell | 4 | 99.0 | 100.0 | 100.0 | 96.0 | 100.0 | 100.0 | 99.0 | 100.0 | 97.0 | 100.0 | 83.0 | 100.0 | 26.0 |
| Mishra01 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Mishra02 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Mishra03 | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| Mishra04 | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| Mishra05 | 2 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 |
| Mishra06 | 2 | 99.0 | 37.0 | 93.0 | 55.0 | 79.0 | 96.0 | 100.0 | 99.0 | 54.0 | 100.0 | 99.0 | 17.0 | 100.0 |
| Mishra07 | 2 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 96.0 | 100.0 |
| Mishra08 | 2 | 96.0 | 100.0 | 100.0 | 92.0 | 92.0 | 100.0 | 99.0 | 100.0 | 100.0 | 99.0 | 64.0 | 100.0 | 100.0 |
| Mishra09 | 3 | 100.0 | 97.0 | 98.0 | 92.0 | 96.0 | 99.0 | 100.0 | 49.0 | 89.0 | 100.0 | 100.0 | 77.0 | 84.0 |
| Mishra10 | 2 | 100.0 | 40.0 | 100.0 | 65.0 | 95.0 | 100.0 | 100.0 | 100.0 | 57.0 | 100.0 | 36.0 | 96.0 | 87.0 |
| Mishra10b | 2 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 86.0 | 100.0 |
| Mishra11 | 2 | 100.0 | 96.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 | 89.0 | 100.0 |
| MullerBrown | 2 | 100.0 | 97.0 | 100.0 | 74.0 | 93.0 | 96.0 | 100.0 | 97.0 | 88.0 | 98.0 | 100.0 | 99.0 | 100.0 |
| MultiGaussian | 2 | 63.0 | 92.0 | 81.0 | 1.0 | 33.0 | 52.0 | 100.0 | 81.0 | 11.0 | 91.0 | 86.0 | 92.0 | 99.0 |
| MultiModal | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 |
| NeedleEye | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 96.0 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 96.0 | 100.0 | 100.0 |
| NewFunction01 | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 100.0 | 0.0 |
| NewFunction02 | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| OddSquare | 2 | 40.0 | 3.0 | 95.0 | 22.0 | 79.0 | 99.0 | 45.0 | 45.0 | 11.0 | 88.0 | 93.0 | 39.0 | 63.0 |
| Osborne | 5 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| Parsopoulos | 2 | 100.0 | 77.0 | 100.0 | 95.0 | 91.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 94.0 | 89.0 | 100.0 |
| Pathological | 2 | 100.0 | 41.0 | 100.0 | 64.0 | 92.0 | 88.0 | 37.0 | 97.0 | 93.0 | 100.0 | 88.0 | 2.0 | 88.0 |
| Paviani | 10 | 1.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 20.0 | 0.0 | 5.0 | 0.0 |
| Peaks | 2 | 92.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 99.0 | 0.0 | 0.0 | 0.0 |
| Penalty01 | 2 | 100.0 | 22.0 | 100.0 | 89.0 | 92.0 | 100.0 | 100.0 | 100.0 | 78.0 | 100.0 | 99.0 | 100.0 | 99.0 |
| Penalty02 | 2 | 88.0 | 100.0 | 98.0 | 32.0 | 95.0 | 93.0 | 39.0 | 94.0 | 49.0 | 66.0 | 96.0 | 77.0 | 12.0 |
| PenHolder | 2 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| PermFunction01 | 2 | 100.0 | 100.0 | 100.0 | 98.0 | 93.0 | 99.0 | 100.0 | 99.0 | 90.0 | 100.0 | 89.0 | 100.0 | 100.0 |
| PermFunction02 | 2 | 100.0 | 100.0 | 99.0 | 99.0 | 95.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| Picheny | 2 | 100.0 | 100.0 | 99.0 | 95.0 | 91.0 | 100.0 | 100.0 | 100.0 | 81.0 | 99.0 | 97.0 | 100.0 | 100.0 |
| Pinter | 2 | 100.0 | 86.0 | 89.0 | 44.0 | 83.0 | 98.0 | 100.0 | 94.0 | 53.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| Plateau | 2 | 100.0 | 82.0 | 100.0 | 91.0 | 100.0 | 100.0 | 100.0 | 100.0 | 92.0 | 100.0 | 5.0 | 100.0 | 58.0 |
| Powell | 4 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 14.0 | 53.0 | 97.0 | 97.0 | 12.0 | 100.0 | 87.0 |
| PowerSum | 4 | 38.0 | 94.0 | 56.0 | 20.0 | 21.0 | 15.0 | 0.0 | 13.0 | 14.0 | 78.0 | 0.0 | 24.0 | 42.0 |
| Price01 | 2 | 99.0 | 99.0 | 100.0 | 88.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 99.0 | 89.0 | 100.0 |
| Price02 | 2 | 73.0 | 8.0 | 71.0 | 7.0 | 58.0 | 62.0 | 97.0 | 96.0 | 14.0 | 100.0 | 62.0 | 93.0 | 100.0 |
| Price03 | 2 | 100.0 | 76.0 | 57.0 | 69.0 | 48.0 | 57.0 | 100.0 | 70.0 | 44.0 | 100.0 | 44.0 | 55.0 | 100.0 |
| Price04 | 2 | 99.0 | 99.0 | 97.0 | 96.0 | 97.0 | 97.0 | 98.0 | 95.0 | 96.0 | 100.0 | 94.0 | 97.0 | 94.0 |
| Qing | 2 | 100.0 | 100.0 | 100.0 | 81.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 95.0 | 100.0 |
| Quadratic | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| Quintic | 2 | 96.0 | 99.0 | 99.0 | 99.0 | 94.0 | 100.0 | 100.0 | 28.0 | 86.0 | 99.0 | 90.0 | 100.0 | 42.0 |
| Rana | 2 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 100.0 | 0.0 | 0.0 | 100.0 |
| Rastrigin | 2 | 44.0 | 73.0 | 100.0 | 7.0 | 80.0 | 87.0 | 100.0 | 100.0 | 16.0 | 99.0 | 91.0 | 100.0 | 100.0 |
| Ratkowsky01 | 4 | 1.0 | 77.0 | 99.0 | 90.0 | 98.0 | 100.0 | 1.0 | 18.0 | 73.0 | 91.0 | 0.0 | 99.0 | 45.0 |
| Ratkowsky02 | 3 | 94.0 | 100.0 | 100.0 | 100.0 | 95.0 | 100.0 | 43.0 | 95.0 | 92.0 | 99.0 | 98.0 | 100.0 | 97.0 |
| ReduxSum | 2 | 100.0 | 100.0 | 100.0 | 87.0 | 99.0 | 100.0 | 100.0 | 100.0 | 96.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Ripple01 | 2 | 26.0 | 0.0 | 95.0 | 3.0 | 77.0 | 69.0 | 29.0 | 61.0 | 2.0 | 45.0 | 39.0 | 1.0 | 0.0 |
| Ripple25 | 2 | 80.0 | 96.0 | 100.0 | 17.0 | 74.0 | 88.0 | 100.0 | 100.0 | 19.0 | 96.0 | 61.0 | 97.0 | 100.0 |
| Rosenbrock | 2 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 82.0 | 100.0 | 100.0 |
| RosenbrockDisc | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 |
| RosenbrockModified | 2 | 57.0 | 19.0 | 69.0 | 13.0 | 28.0 | 37.0 | 100.0 | 92.0 | 15.0 | 86.0 | 68.0 | 66.0 | 100.0 |
| RotatedEllipse01 | 2 | 100.0 | 100.0 | 100.0 | 90.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| RotatedEllipse02 | 2 | 100.0 | 100.0 | 100.0 | 90.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Salomon | 2 | 27.0 | 97.0 | 37.0 | 0.0 | 37.0 | 49.0 | 9.0 | 47.0 | 3.0 | 21.0 | 84.0 | 0.0 | 1.0 |
| Sargan | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 99.0 | 100.0 | 100.0 |
| SawtoothXY | 2 | 100.0 | 99.0 | 100.0 | 54.0 | 93.0 | 100.0 | 100.0 | 98.0 | 70.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Schaffer01 | 2 | 11.0 | 40.0 | 86.0 | 0.0 | 67.0 | 98.0 | 6.0 | 61.0 | 6.0 | 83.0 | 100.0 | 1.0 | 5.0 |
| Schaffer02 | 2 | 13.0 | 40.0 | 100.0 | 1.0 | 75.0 | 100.0 | 9.0 | 100.0 | 30.0 | 92.0 | 100.0 | 6.0 | 6.0 |
| Schaffer03 | 2 | 17.0 | 49.0 | 100.0 | 3.0 | 79.0 | 98.0 | 3.0 | 94.0 | 25.0 | 88.0 | 93.0 | 0.0 | 21.0 |
| Schaffer04 | 2 | 13.0 | 34.0 | 99.0 | 1.0 | 78.0 | 94.0 | 2.0 | 95.0 | 14.0 | 79.0 | 85.0 | 0.0 | 4.0 |
| SchmidtVetters | 3 | 100.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Schwefel01 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 100.0 | 100.0 |
| Schwefel02 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Schwefel04 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 91.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| Schwefel06 | 2 | 99.0 | 90.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 6.0 | 100.0 | 57.0 | 96.0 | 100.0 | 92.0 |
| Schwefel20 | 2 | 95.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 22.0 | 100.0 | 100.0 | 92.0 | 100.0 | 90.0 |
| Schwefel21 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 18.0 | 100.0 | 89.0 | 98.0 | 100.0 | 89.0 |
| Schwefel22 | 2 | 97.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 22.0 | 100.0 | 99.0 | 99.0 | 100.0 | 82.0 |
| Schwefel26 | 2 | 100.0 | 9.0 | 100.0 | 32.0 | 70.0 | 97.0 | 100.0 | 100.0 | 34.0 | 96.0 | 96.0 | 100.0 | 100.0 |
| Schwefel36 | 2 | 100.0 | 100.0 | 100.0 | 0.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Shekel05 | 4 | 89.0 | 55.0 | 59.0 | 55.0 | 69.0 | 71.0 | 77.0 | 76.0 | 43.0 | 98.0 | 54.0 | 68.0 | 95.0 |
| Shekel07 | 4 | 73.0 | 63.0 | 57.0 | 57.0 | 71.0 | 77.0 | 73.0 | 75.0 | 44.0 | 96.0 | 53.0 | 70.0 | 89.0 |
| Shekel10 | 4 | 61.0 | 61.0 | 46.0 | 55.0 | 65.0 | 77.0 | 81.0 | 60.0 | 30.0 | 97.0 | 52.0 | 82.0 | 79.0 |
| Shubert01 | 2 | 95.0 | 96.0 | 100.0 | 20.0 | 82.0 | 99.0 | 86.0 | 99.0 | 56.0 | 100.0 | 95.0 | 60.0 | 100.0 |
| Shubert03 | 2 | 92.0 | 75.0 | 100.0 | 7.0 | 81.0 | 100.0 | 93.0 | 99.0 | 27.0 | 100.0 | 97.0 | 9.0 | 100.0 |
| Shubert04 | 2 | 94.0 | 80.0 | 100.0 | 16.0 | 91.0 | 99.0 | 96.0 | 100.0 | 50.0 | 100.0 | 97.0 | 72.0 | 100.0 |
| Simpleton | 10 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 0.0 |
| SineEnvelope | 2 | 9.0 | 0.0 | 18.0 | 0.0 | 15.0 | 12.0 | 1.0 | 17.0 | 2.0 | 49.0 | 47.0 | 0.0 | 3.0 |
| Sinusoidal | 2 | 99.0 | 11.0 | 97.0 | 32.0 | 87.0 | 97.0 | 100.0 | 100.0 | 65.0 | 100.0 | 96.0 | 100.0 | 94.0 |
| SixHumpCamel | 2 | 100.0 | 99.0 | 100.0 | 86.0 | 92.0 | 100.0 | 100.0 | 100.0 | 79.0 | 100.0 | 97.0 | 100.0 | 100.0 |
| Sodp | 2 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Sphere | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| SphericalSinc | 2 | 93.0 | 15.0 | 99.0 | 16.0 | 94.0 | 100.0 | 100.0 | 100.0 | 64.0 | 100.0 | 98.0 | 100.0 | 100.0 |
| Spike | 2 | 57.0 | 80.0 | 99.0 | 1.0 | 62.0 | 78.0 | 45.0 | 97.0 | 1.0 | 76.0 | 16.0 | 25.0 | 81.0 |
| Step01 | 2 | 100.0 | 0.0 | 100.0 | 93.0 | 91.0 | 100.0 | 100.0 | 100.0 | 85.0 | 88.0 | 100.0 | 100.0 | 72.0 |
| Step02 | 2 | 100.0 | 0.0 | 100.0 | 92.0 | 91.0 | 100.0 | 100.0 | 100.0 | 86.0 | 100.0 | 98.0 | 100.0 | 67.0 |
| Step03 | 2 | 100.0 | 1.0 | 100.0 | 100.0 | 96.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 97.0 | 100.0 | 64.0 |
| Stochastic | 2 | 27.0 | 0.0 | 99.0 | 44.0 | 82.0 | 95.0 | 100.0 | 0.0 | 0.0 | 0.0 | 26.0 | 0.0 | 0.0 |
| StretchedV | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 97.0 | 98.0 | 100.0 | 100.0 | 100.0 | 100.0 | 98.0 | 68.0 | 100.0 |
| StyblinskiTang | 2 | 100.0 | 64.0 | 100.0 | 58.0 | 96.0 | 100.0 | 100.0 | 100.0 | 67.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| TestTubeHolder | 2 | 63.0 | 33.0 | 97.0 | 7.0 | 76.0 | 64.0 | 100.0 | 99.0 | 10.0 | 99.0 | 54.0 | 58.0 | 100.0 |
| ThreeHumpCamel | 2 | 100.0 | 99.0 | 98.0 | 80.0 | 95.0 | 99.0 | 100.0 | 100.0 | 72.0 | 99.0 | 100.0 | 100.0 | 100.0 |
| Thurber | 7 | 0.0 | 0.0 | 41.0 | 59.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 22.0 | 0.0 | 6.0 | 0.0 |
| Treccani | 2 | 100.0 | 97.0 | 100.0 | 99.0 | 98.0 | 100.0 | 100.0 | 100.0 | 93.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Trefethen | 2 | 8.0 | 7.0 | 35.0 | 0.0 | 8.0 | 31.0 | 6.0 | 22.0 | 2.0 | 51.0 | 19.0 | 0.0 | 3.0 |
| Trid | 6 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 8.0 | 80.0 | 66.0 | 90.0 | 15.0 | 100.0 | 83.0 |
| TridiagonalMatrix | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 95.0 | 100.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Trigonometric01 | 2 | 99.0 | 88.0 | 100.0 | 76.0 | 83.0 | 99.0 | 100.0 | 97.0 | 57.0 | 91.0 | 99.0 | 100.0 | 99.0 |
| Trigonometric02 | 2 | 98.0 | 100.0 | 100.0 | 68.0 | 89.0 | 100.0 | 100.0 | 100.0 | 51.0 | 75.0 | 97.0 | 100.0 | 0.0 |
| Tripod | 2 | 89.0 | 58.0 | 73.0 | 71.0 | 75.0 | 76.0 | 100.0 | 23.0 | 61.0 | 99.0 | 69.0 | 74.0 | 85.0 |
| Tsoulos | 2 | 65.0 | 98.0 | 100.0 | 22.0 | 80.0 | 92.0 | 100.0 | 100.0 | 27.0 | 100.0 | 95.0 | 96.0 | 100.0 |
| Ursem01 | 2 | 100.0 | 83.0 | 100.0 | 80.0 | 91.0 | 100.0 | 100.0 | 100.0 | 98.0 | 100.0 | 99.0 | 100.0 | 100.0 |
| Ursem03 | 2 | 80.0 | 67.0 | 100.0 | 26.0 | 87.0 | 99.0 | 100.0 | 12.0 | 50.0 | 100.0 | 98.0 | 97.0 | 68.0 |
| Ursem04 | 2 | 100.0 | 100.0 | 100.0 | 75.0 | 99.0 | 100.0 | 100.0 | 39.0 | 98.0 | 99.0 | 100.0 | 100.0 | 100.0 |
| UrsemWaves | 2 | 100.0 | 100.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 |
| VenterSobiezcczanskiSobieski | 2 | 100.0 | 42.0 | 100.0 | 31.0 | 87.0 | 95.0 | 100.0 | 100.0 | 31.0 | 98.0 | 98.0 | 100.0 | 95.0 |
| Vincent | 2 | 100.0 | 80.0 | 100.0 | 90.0 | 58.0 | 63.0 | 90.0 | 94.0 | 87.0 | 100.0 | 95.0 | 90.0 | 100.0 |
| Watson | 6 | 30.0 | 99.0 | 100.0 | 100.0 | 100.0 | 0.0 | 0.0 | 44.0 | 0.0 | 86.0 | 0.0 | 71.0 | 66.0 |
| Wavy | 2 | 28.0 | 39.0 | 100.0 | 7.0 | 84.0 | 96.0 | 94.0 | 100.0 | 36.0 | 99.0 | 98.0 | 100.0 | 100.0 |
| WayburnSeader01 | 2 | 100.0 | 100.0 | 100.0 | 98.0 | 90.0 | 99.0 | 100.0 | 99.0 | 89.0 | 99.0 | 95.0 | 99.0 | 100.0 |
| WayburnSeader02 | 2 | 100.0 | 100.0 | 100.0 | 87.0 | 100.0 | 100.0 | 100.0 | 97.0 | 100.0 | 100.0 | 96.0 | 99.0 | 100.0 |
| WayburnSeader03 | 2 | 100.0 | 100.0 | 100.0 | 85.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Weierstrass | 2 | 98.0 | 0.0 | 100.0 | 86.0 | 88.0 | 100.0 | 100.0 | 0.0 | 72.0 | 45.0 | 0.0 | 100.0 | 0.0 |
| Whitley | 2 | 12.0 | 24.0 | 22.0 | 2.0 | 28.0 | 37.0 | 5.0 | 19.0 | 3.0 | 13.0 | 24.0 | 0.0 | 5.0 |
| Wolfe | 3 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| XinSheYang01 | 2 | 71.0 | 0.0 | 100.0 | 61.0 | 84.0 | 99.0 | 100.0 | 9.0 | 6.0 | 38.0 | 51.0 | 1.0 | 0.0 |
| XinSheYang02 | 2 | 98.0 | 97.0 | 94.0 | 22.0 | 72.0 | 90.0 | 100.0 | 14.0 | 39.0 | 100.0 | 94.0 | 100.0 | 68.0 |
| XinSheYang03 | 2 | 7.0 | 15.0 | 28.0 | 4.0 | 3.0 | 9.0 | 37.0 | 66.0 | 1.0 | 91.0 | 15.0 | 16.0 | 100.0 |
| XinSheYang04 | 2 | 56.0 | 2.0 | 93.0 | 7.0 | 73.0 | 87.0 | 100.0 | 19.0 | 31.0 | 99.0 | 91.0 | 98.0 | 69.0 |
| Xor | 9 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| YaoLiu04 | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 19.0 | 100.0 | 94.0 | 97.0 | 100.0 | 94.0 |
| YaoLiu09 | 2 | 56.0 | 79.0 | 100.0 | 7.0 | 81.0 | 93.0 | 100.0 | 100.0 | 26.0 | 100.0 | 93.0 | 99.0 | 100.0 |
| Zacharov | 2 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 99.0 | 100.0 | 100.0 |
| Zagros | 2 | 16.0 | 0.0 | 47.0 | 0.0 | 67.0 | 35.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 68.0 | 0.0 |
| ZeroSum | 2 | 0.0 | 0.0 | 97.0 | 79.0 | 98.0 | 99.0 | 96.0 | 0.0 | 98.0 | 46.0 | 0.0 | 100.0 | 0.0 |
| Zettl | 2 | 99.0 | 100.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.0 | 99.0 | 98.0 | 100.0 | 100.0 |
| Zimmerman | 2 | 92.0 | 0.0 | 45.0 | 43.0 | 45.0 | 54.0 | 0.0 | 0.0 | 10.0 | 0.0 | 43.0 | 40.0 | 0.0 |
| Zirilli | 2 | 100.0 | 99.0 | 100.0 | 83.0 | 98.0 | 97.0 | 100.0 | 100.0 | 83.0 | 100.0 | 100.0 | 100.0 | 100.0 |