Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions A
 N-D Test Functions A¶
N-D Test Functions A¶Ackley01 objective function.
The Ackley01 global optimization problem is a multimodal minimization problem defined as follows:
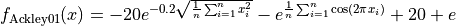
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-35, 35]](_images/math/c122c94f2d4d69851226e252ac233dd7d36118bc.png) for
for  .
.
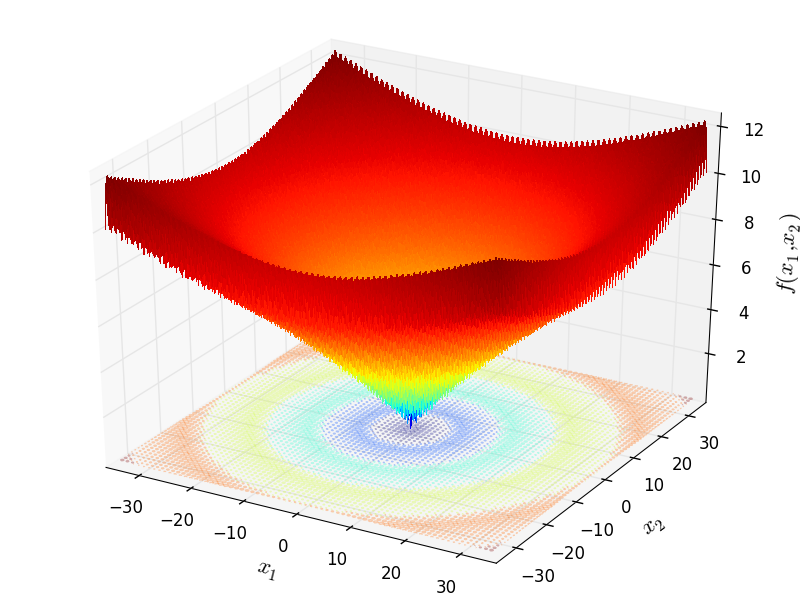
Two-dimensional Ackley01 function
Global optimum:  for
for 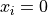 for
for

Adorio, E. MVF - “Multivariate Test Functions Library in C for Unconstrained Global Optimization”, 2005
Todo
the -0.2 factor in the exponent of the first term is given as -0.02 in Jamil et al.
Ackley02 objective function.
The Ackley02 global optimization problem is a multimodal minimization problem defined as follows:
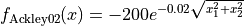
with ![x_i \in [-32, 32]](_images/math/b256b356be385a92f6c093826bbb33b853901a6f.png) for
for 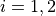 .
.
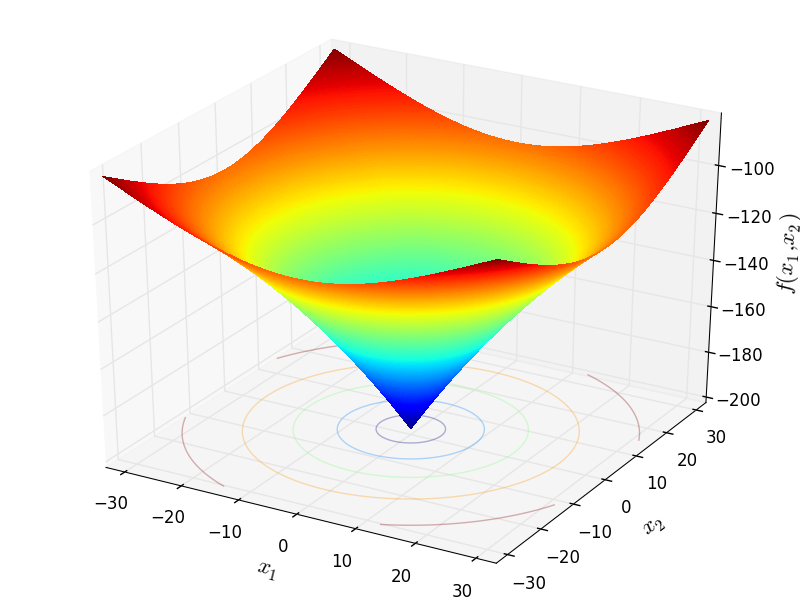
Two-dimensional Ackley02 function
Global optimum: 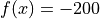 for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Ackley03 objective function.
The Ackley03 global optimization problem is a multimodal minimization problem defined as follows:
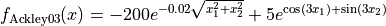
with ![x_i \in [-32, 32]](_images/math/b256b356be385a92f6c093826bbb33b853901a6f.png) for
for 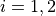 .
.
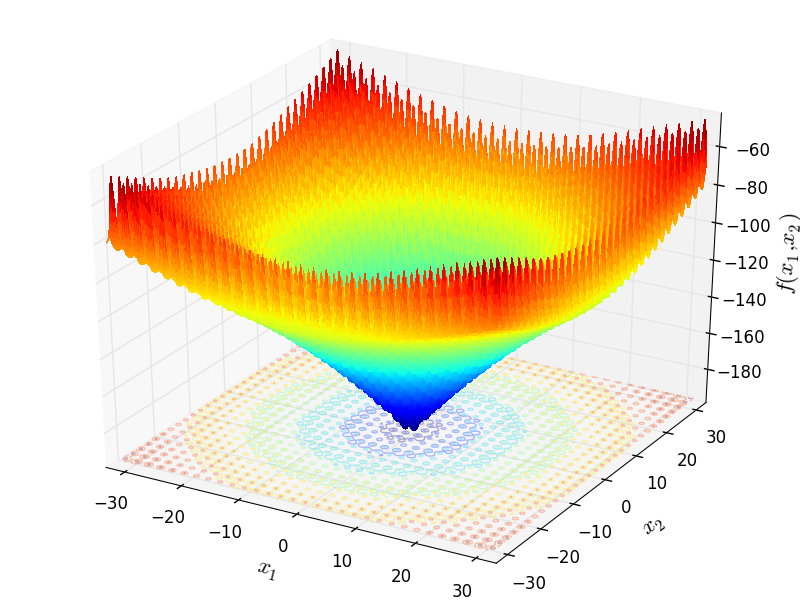
Two-dimensional Ackley03 function
Global optimum: 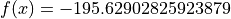 for
for ![x = [-0.68255758, -0.36070859]](_images/math/56d62839fb68da6855bc12642c2fa2d246e2c0ea.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
I think the minus sign is missing in front of the first term in eqn3 in Jamil. This changes the global minimum
Ackley04 objective function.
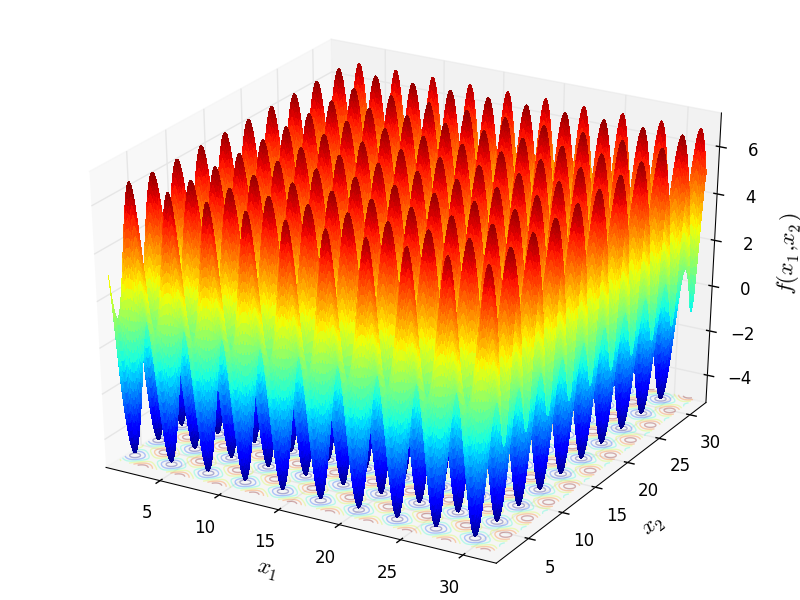
Two-dimensional Ackley04 function
Adjiman objective function.
The Adjiman global optimization problem is a multimodal minimization problem defined as follows:
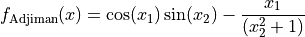
with, ![x_1\in [-1, 2]](_images/math/dcdba128ba5a28bfda007b5e3f18eb578f649de1.png) and
and ![x_2\in [-1, 1]](_images/math/500e2f5c595b3c70e0946c0013cf6aaebe27a6b1.png) .
.
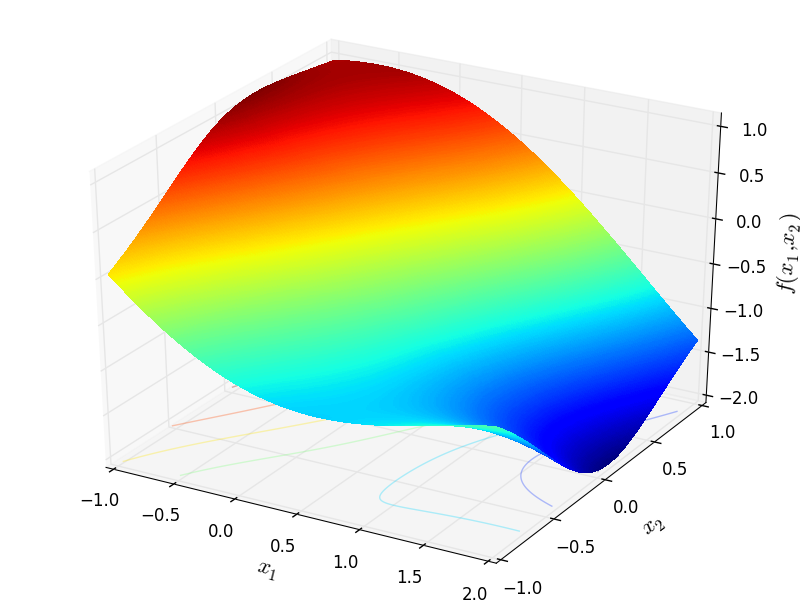
Two-dimensional Adjiman function
Global optimum: 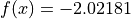 for
for ![x = [2.0, 0.10578]](_images/math/95e2da5ed80fc404a586bc249fe12d945f2ff4d3.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Alpine01 objective function.
The Alpine01 global optimization problem is a multimodal minimization problem defined as follows:
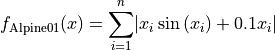
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-10, 10]](_images/math/2b179dc5b6b6f3b7e0eee8eff274bef7d6fd91cd.png) for
for  .
.
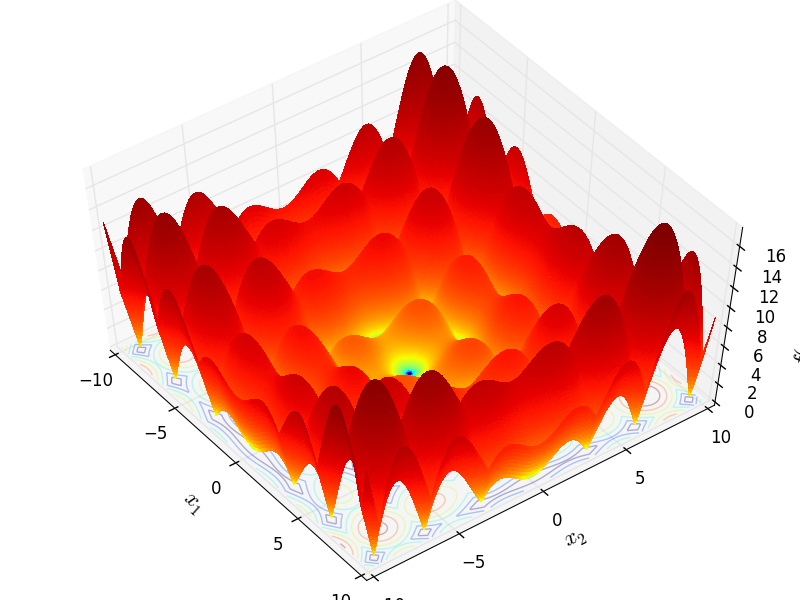
Two-dimensional Alpine01 function
Global optimum:  for
for 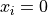 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Alpine02 objective function.
The Alpine02 global optimization problem is a multimodal minimization problem defined as follows:
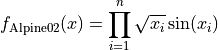
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0,
10]](_images/math/5fc92e5e5cfd66e784667ded97a20543dfc8ed84.png) for
for  .
.
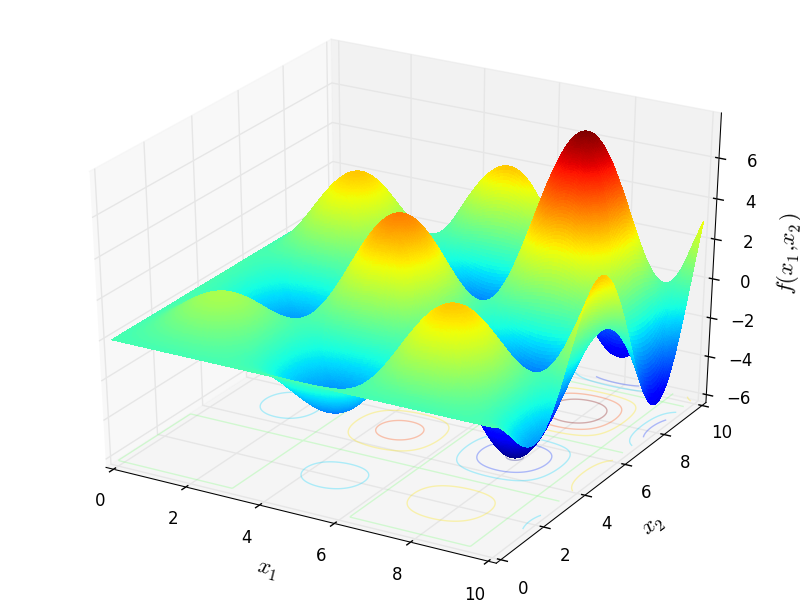
Two-dimensional Alpine02 function
Global optimum:  for
for ![x =
[7.91705268, 4.81584232]](_images/math/7200d4186cc9b80e59ac46b2ea29aa4cf204012e.png) for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
eqn 7 in has the wrong global minimum value.
AMGM objective function.
The AMGM (Arithmetic Mean - Geometric Mean Equality) global optimization problem is a multimodal minimization problem defined as follows
![f_{\text{AMGM}}(x) = \left ( \frac{1}{n} \sum_{i=1}^{n} x_i -
\sqrt[n]{ \prod_{i=1}^{n} x_i} \right )^2](_images/math/f8e4be09992d278ea83b524ec6f84e013fd396c6.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[0, 10]](_images/math/4db115363cc95ed6512c64a2e9f39c21ca84d628.png) for
for  .
.
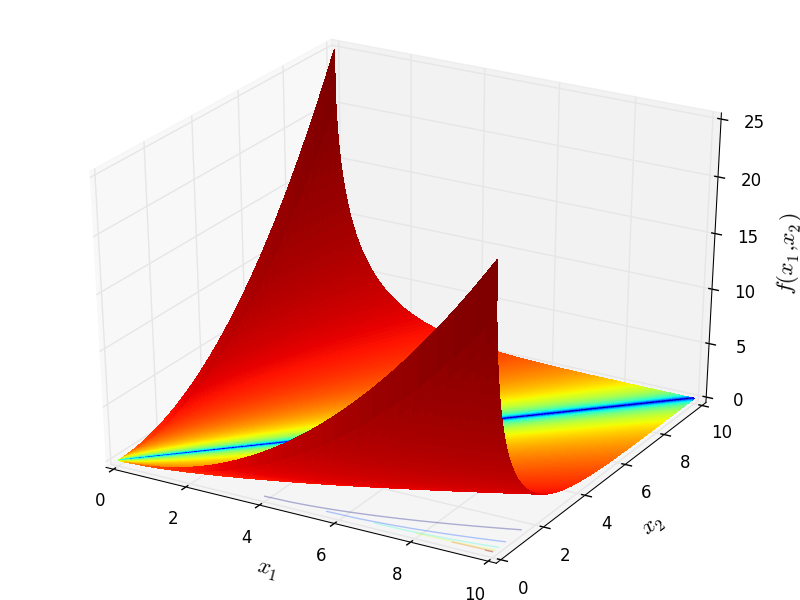
Two-dimensional AMGM function
Global optimum:  for
for 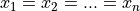 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO