Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions B
 N-D Test Functions B¶
N-D Test Functions B¶Bartels-Conn objective function.
The BartelsConn global optimization problem is a multimodal minimization problem defined as follows:
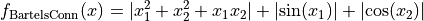
with ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
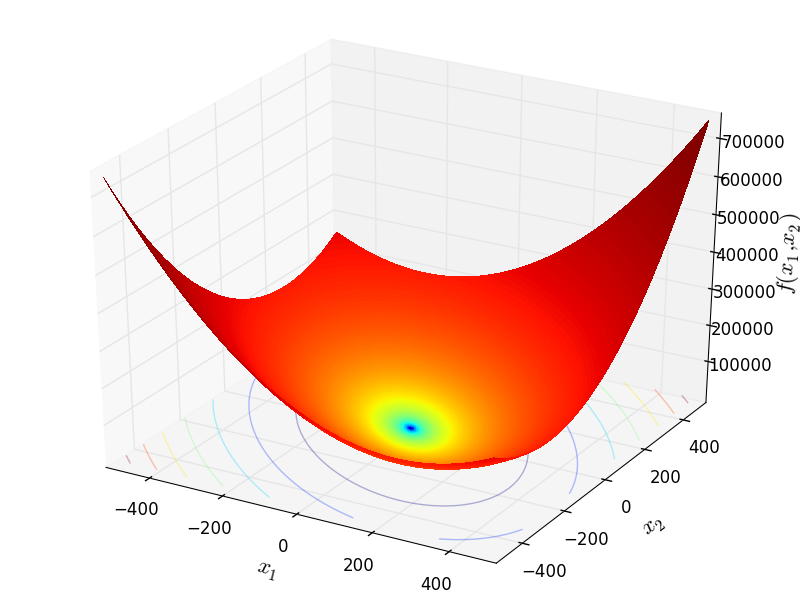
Two-dimensional BartelsConn function
Global optimum: 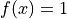 for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Beale objective function.
The Beale global optimization problem is a multimodal minimization problem defined as follows:
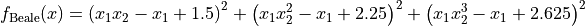
with ![x_i \in [-4.5, 4.5]](_images/math/26bb383ff5ec79e25acabb0d6267667a98f7e541.png) for
for  .
.
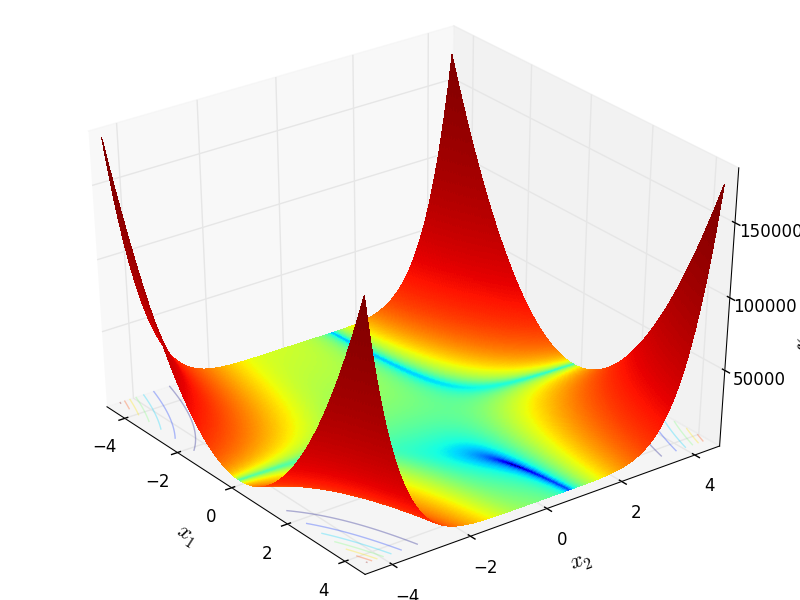
Two-dimensional Beale function
Global optimum:  for
for ![x=[3, 0.5]](_images/math/85c7f5589e443744e424a1bfc2015ca1c0ce4830.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BiggsExp02 objective function.
The BiggsExp02 global optimization problem is a multimodal minimization problem defined as follows
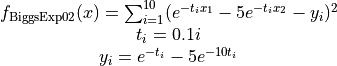
with ![x_i \in [0, 20]](_images/math/e5cccc28ef66f0ce2a2510a87fb96ecd83484bd5.png) for
for  .
.
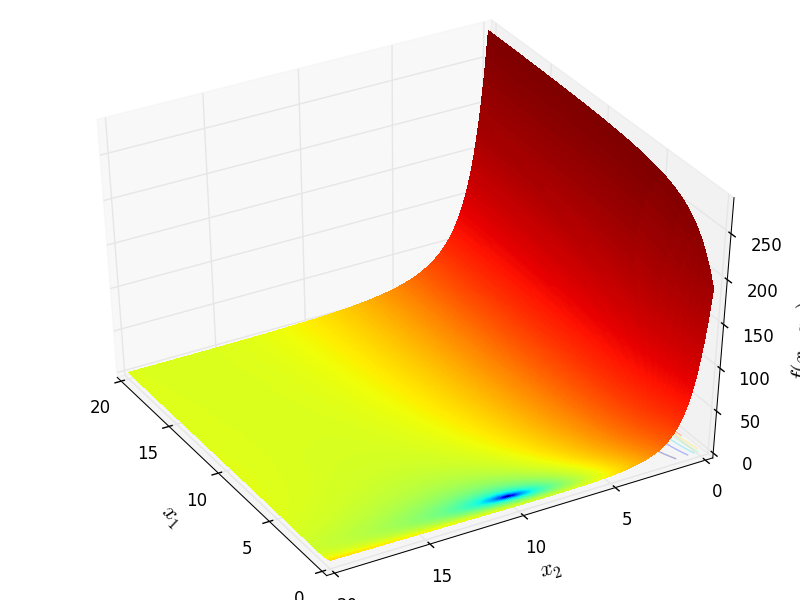
Two-dimensional BiggsExp02 function
Global optimum:  for
for ![x = [1, 10]](_images/math/4469a998cb783397829dde97f3aba215d71a0f54.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BiggsExp03 objective function.
The BiggsExp03 global optimization problem is a multimodal minimization problem defined as follows
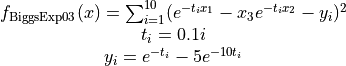
with ![x_i \in [0, 20]](_images/math/e5cccc28ef66f0ce2a2510a87fb96ecd83484bd5.png) for
for 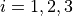 .
.
Global optimum:  for
for ![x = [1, 10, 5]](_images/math/f2b3641e15883c50428eaff348a73d8a3f27d86f.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BiggsExp04 objective function.
The BiggsExp04 global optimization problem is a multimodal minimization problem defined as follows
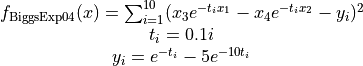
with ![x_i \in [0, 20]](_images/math/e5cccc28ef66f0ce2a2510a87fb96ecd83484bd5.png) for
for 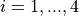 .
.
Global optimum:  for
for ![x = [1, 10, 1, 5]](_images/math/5da119e29ac2f7bc8dc8e50053dc58b105eef0fc.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BiggsExp05 objective function.
The BiggsExp05 global optimization problem is a multimodal minimization problem defined as follows
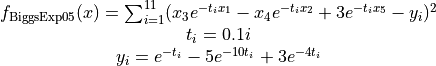
with ![x_i \in [0, 20]](_images/math/e5cccc28ef66f0ce2a2510a87fb96ecd83484bd5.png) for
for 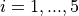 .
.
Global optimum:  for
for ![x = [1, 10, 1, 5, 4]](_images/math/13c8918fb7c75e83ed170b17ea4a7693ecf7e282.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BiggsExp06 objective function.
Bird objective function.
The Bird global optimization problem is a multimodal minimization problem defined as follows
![f_{\text{Bird}}(x) = \left(x_1 - x_2\right)^{2} + e^{\left[1 -
\sin\left(x_1\right) \right]^{2}} \cos\left(x_2\right) + e^{\left[1 -
\cos\left(x_2\right)\right]^{2}} \sin\left(x_1\right)](_images/math/dbd1e56eaa0f671263da699329e544f0941defce.png)
with ![x_i \in [-2\pi, 2\pi]](_images/math/550244574963351248b8b30f9d583095c065c220.png)
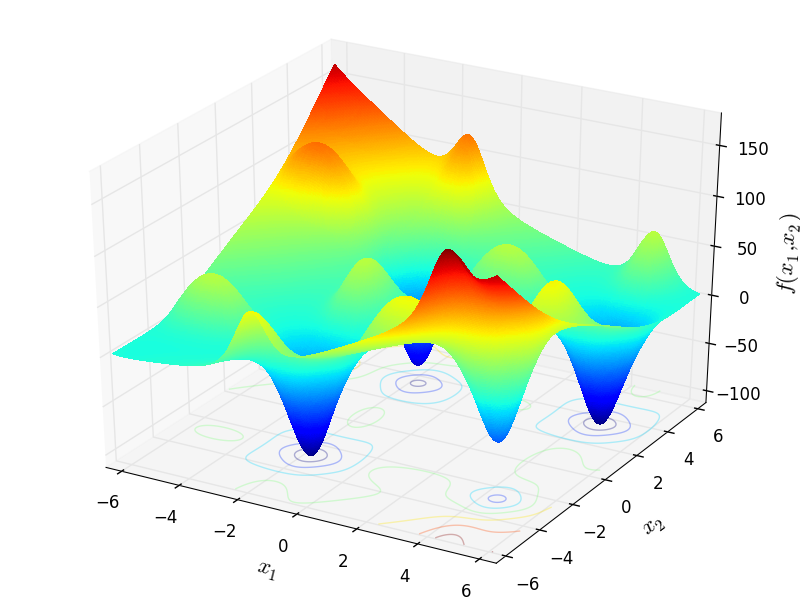
Two-dimensional Bird function
Global optimum: 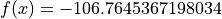 for
for ![x
= [4.701055751981055, 3.152946019601391]](_images/math/26441a1c6959f7412cd5461ba5f4f3be1cdb3580.png) or
or ![x =
[-1.582142172055011, -3.130246799635430]](_images/math/733481f594e27f3f3f22386229ae46645e8abb02.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Bohachevsky 1 objective function.
The Bohachevsky 1 global optimization problem is a multimodal minimization problem defined as follows
![f_{\text{Bohachevsky01}}(x) = \sum_{i=1}^{n-1}\left[x_i^2 + 2x_{i+1}^2 - 0.3 \cos(3 \pi x_i) - 0.4 \cos(4 \pi x_{i+1}) + 0.7 \right]](_images/math/908e6b54a30caa0c617c2799b469fbe76df72dcc.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-15, 15]](_images/math/1d7be2a6d990e540b8718838a44790385b7c6b18.png) for
for  .
.
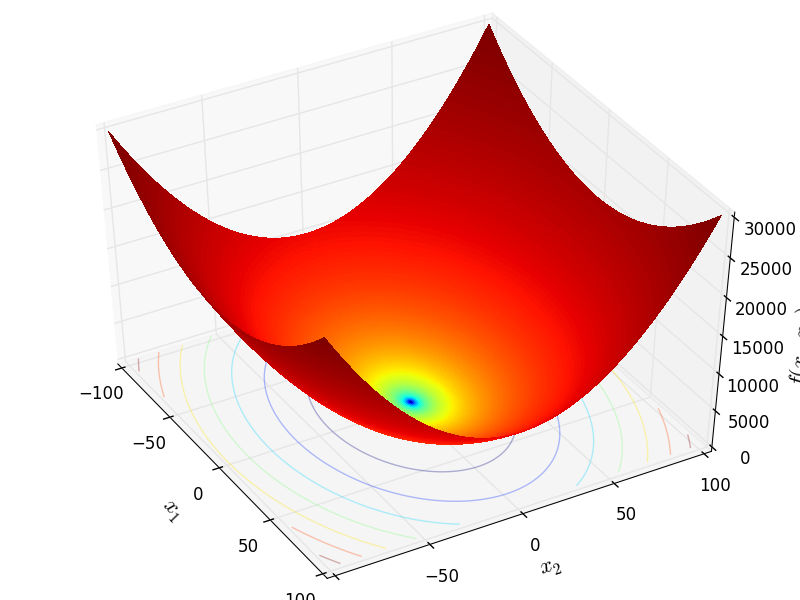
Two-dimensional Bohachevsky01 function
Global optimum:  for
for 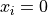 for
for 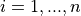
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
equation needs to be fixed up in the docstring. see Jamil#17
Bohachevsky 2 objective function.
The Bohachevsky 2 global optimization problem is a multimodal minimization problem defined as follows
![f_{\text{Bohachevsky02}}(x) = \sum_{i=1}^{n-1}\left[x_i^2 + 2 x_{i+1}^2 - 0.3 \cos(3 \pi x_i) - 0.4 \cos(4 \pi x_{i + 1}) + 0.7 \right]](_images/math/7fa87ff98faa6d649cb74c37f60c3121f05b0e9f.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-15, 15]](_images/math/1d7be2a6d990e540b8718838a44790385b7c6b18.png) for
for  .
.
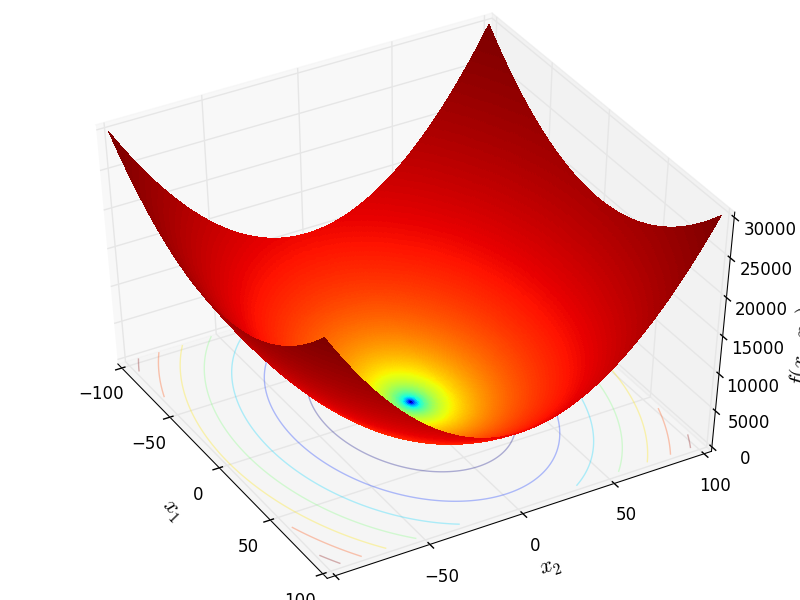
Two-dimensional Bohachevsky02 function
Global optimum:  for
for 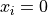 for
for 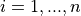
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
equation needs to be fixed up in the docstring. Jamil is also wrong. There should be no 0.4 factor in front of the cos term
Bohachevsky 3 objective function.
The Bohachevsky 3 global optimization problem is a multimodal minimization problem defined as follows
![f_{\text{Bohachevsky02}}(x) = \sum_{i=1}^{n-1}\left[x_i^2 + 2 x_{i+1}^2 - 0.3 \cos(3 \pi x_i) - 0.4 \cos(4 \pi x_{i + 1}) + 0.7 \right]](_images/math/7fa87ff98faa6d649cb74c37f60c3121f05b0e9f.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-15, 15]](_images/math/1d7be2a6d990e540b8718838a44790385b7c6b18.png) for
for  .
.
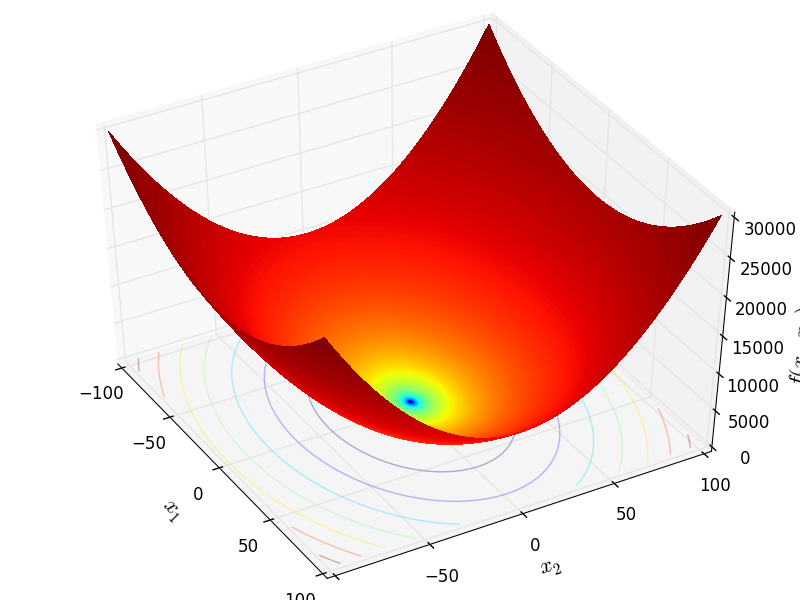
Two-dimensional Bohachevsky03 function
Global optimum:  for
for 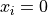 for
for 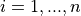
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
equation needs to be fixed up in the docstring. Jamil#19
Booth objective function.
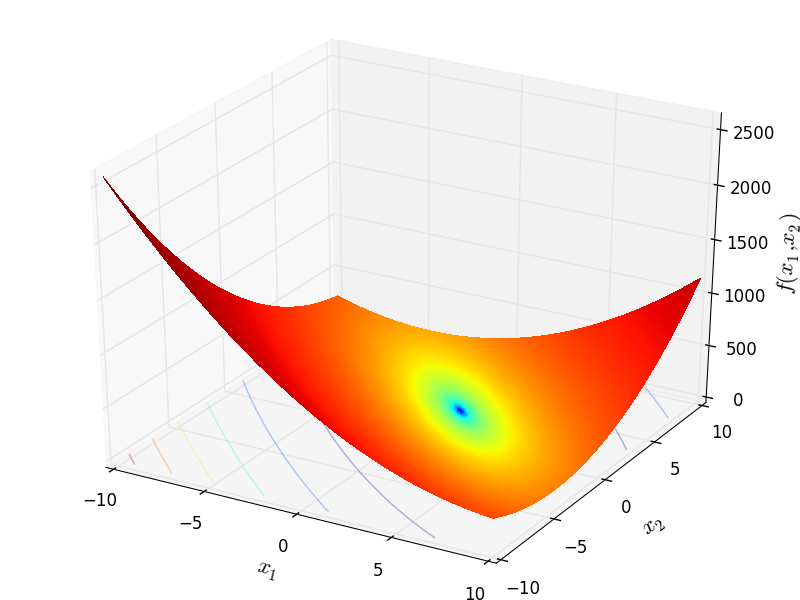
Two-dimensional Booth function
BoxBetts objective function.
The BoxBetts global optimization problem is a multimodal minimization problem defined as follows
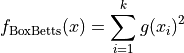
Where, in this exercise:
![g(x) = e^{-0.1i x_1} - e^{-0.1i x_2} - x_3\left[e^{-0.1i} - e^{-i}\right]](_images/math/12af1df21b03965a3a57178189214012e3b67dcc.png)
And 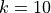 .
.
Here, ![x_1\in [0.9, 1.2], x_2\in [9, 11.2], x_3\in [0.9, 1.2]](_images/math/64605ecdcd71a2b9ea57d8740e31e2eec6e0edc7.png) .
.
Global optimum:  for
for ![x = [1, 10, 1]](_images/math/f4316a1ea66b4a22d540e02f83ba48b526c7de6e.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Brad objective function.
Branin01 objective function.
The Branin01 global optimization problem is a multimodal minimization problem defined as follows
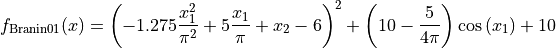
with ![x_1\in [-5, 10], x_2\in [0, 15]](_images/math/e23451af7b29735a683f88828e28491f99a04446.png)
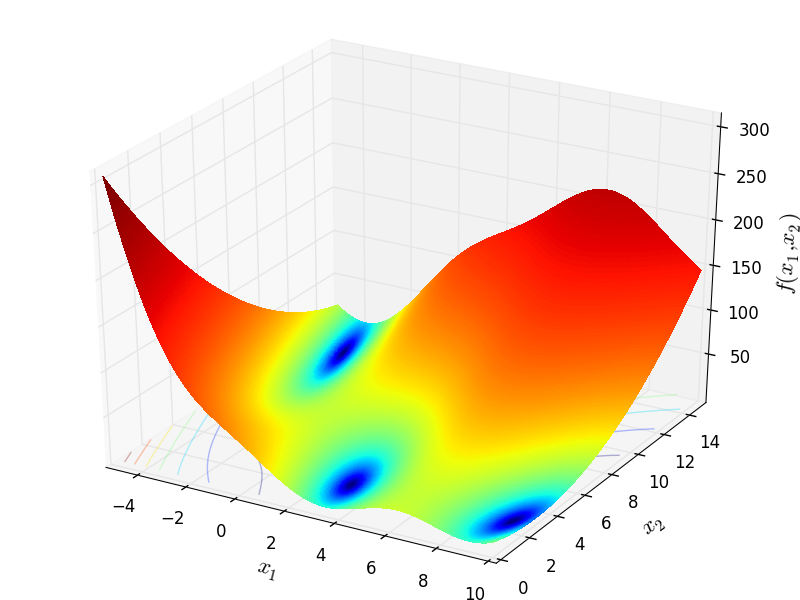
Two-dimensional Branin01 function
Global optimum: 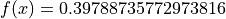 for
for ![x =
[-\pi, 12.275]](_images/math/cea93b7af006ab40774b110c9d2b0b4889f869eb.png) or
or ![x = [\pi, 2.275]](_images/math/7b05947d6a5c50c4470760f40bc2f5383b7b8523.png) or
or ![x = [3\pi, 2.475]](_images/math/a8c32acff871b9780354e4ef7bcc1a1d4bd3c3df.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil#22, one of the solutions is different
Branin02 objective function.
The Branin02 global optimization problem is a multimodal minimization problem defined as follows
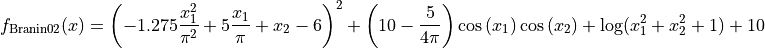
with ![x_i \in [-5, 15]](_images/math/b4e877d210b8c99a277da78c333f2e87d93feeae.png) for
for  .
.
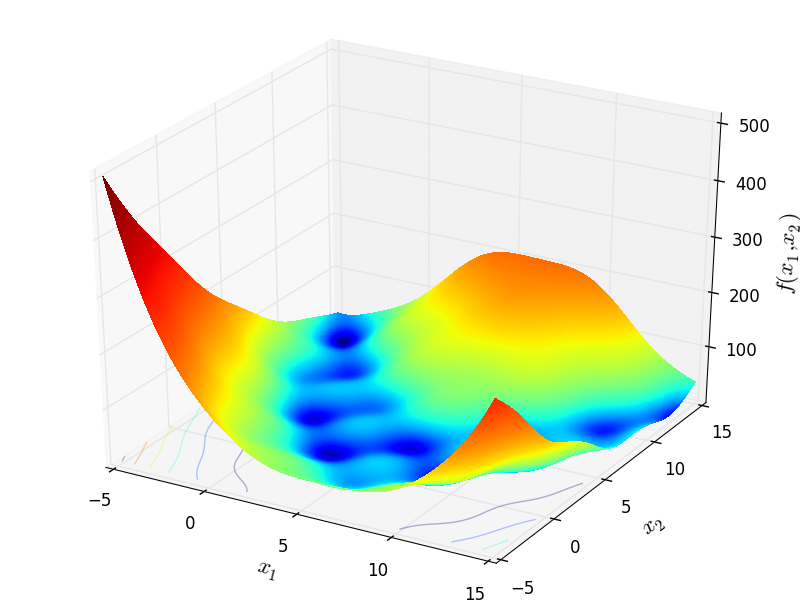
Two-dimensional Branin02 function
Global optimum: 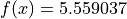 for
for ![x = [-3.2, 12.53]](_images/math/9afa618d44a61e70f161c5ad9ca66ca4c0d94f5c.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Brent objective function.
The Brent global optimization problem is a multimodal minimization problem defined as follows:
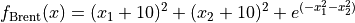
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
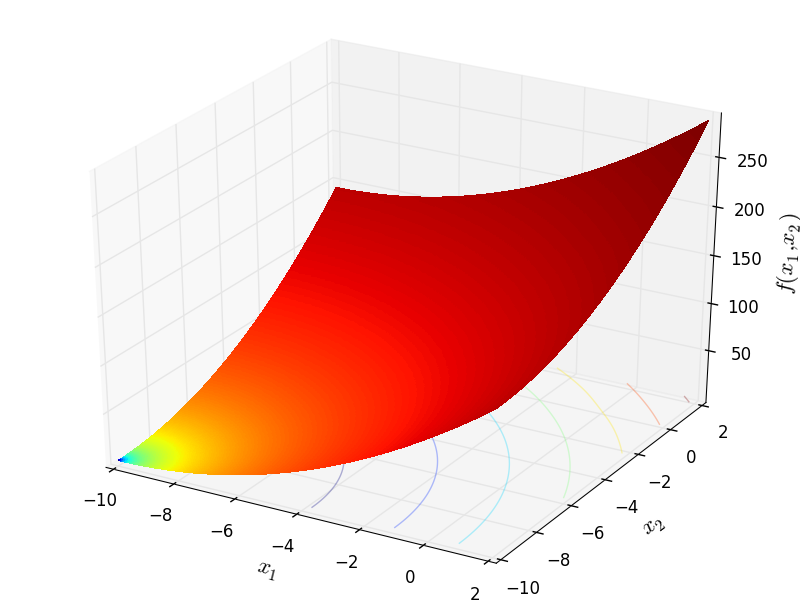
Two-dimensional Brent function
Global optimum:  for
for ![x = [-10, -10]](_images/math/8d58cf75dba2e589218b5b9f6e8a5a1893e2bc30.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
solution is different to Jamil#24
Brown objective function.
The Brown global optimization problem is a multimodal minimization problem defined as follows:
![f_{\text{Brown}}(x) = \sum_{i=1}^{n-1}\left[
\left(x_i^2\right)^{x_{i + 1}^2 + 1}
+ \left(x_{i + 1}^2\right)^{x_i^2 + 1}\right]](_images/math/722fd54605f9442bcc19f1b2635ffc374314a8cc.png)
with ![x_i \in [-1, 4]](_images/math/0c11019405ea0856aeb25fbdd6d05b00b32e7e0e.png) for
for 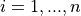 .
.
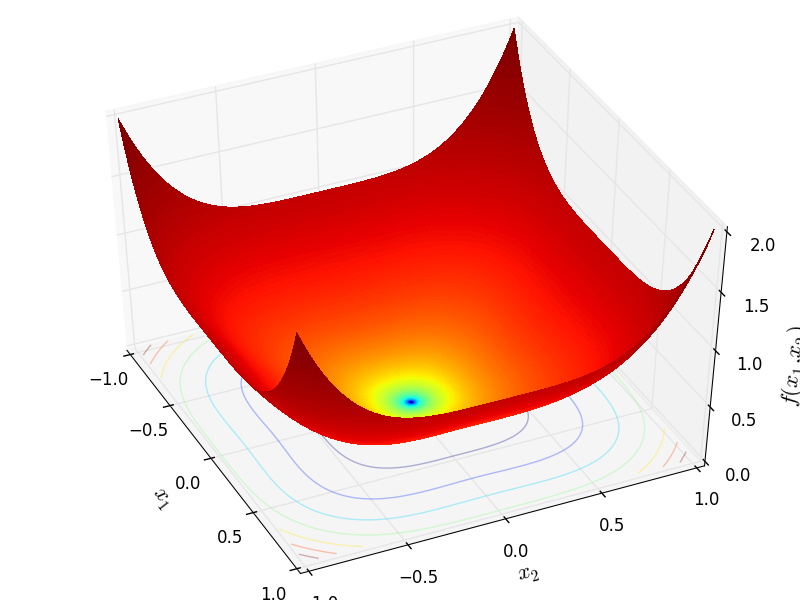
Two-dimensional Brown function
Global optimum: 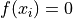 for
for 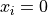 for
for
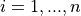
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
BuecheRastrigin objective function.
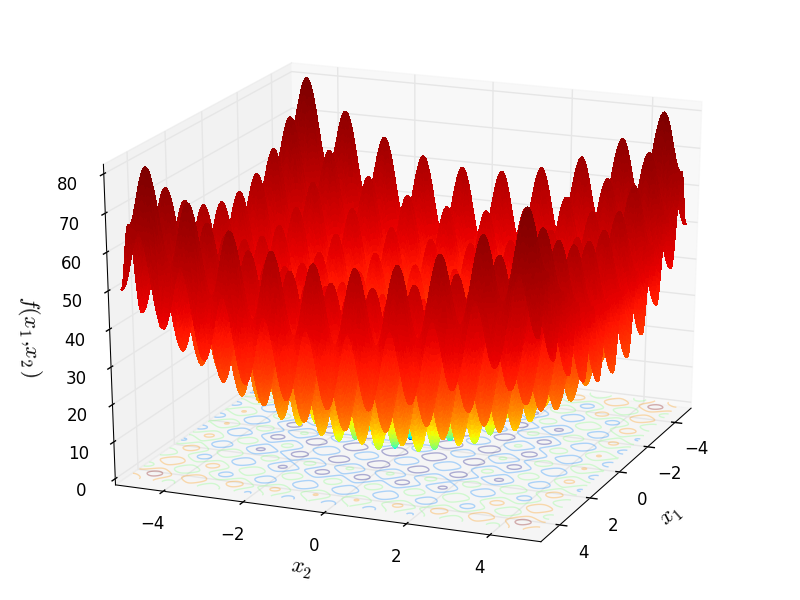
Two-dimensional BuecheRastrigin function
Bukin02 objective function.
The Bukin02 global optimization problem is a multimodal minimization problem defined as follows:
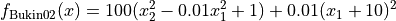
with ![x_1\in [-15, -5], x_2\in [-3, 3]](_images/math/6a2089f48bedd800a6dff64a97d2e3a7459626fa.png)
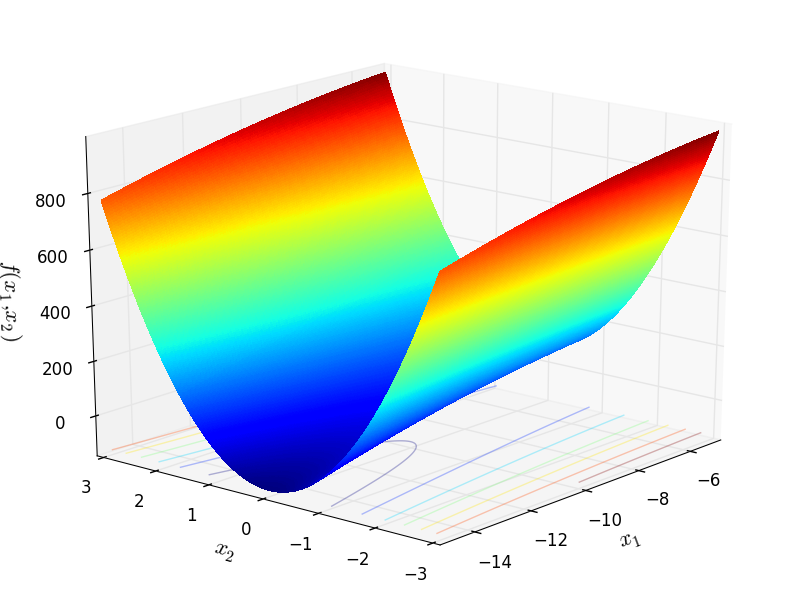
Two-dimensional Bukin02 function
Global optimum: 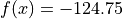 for
for ![x = [-15, 0]](_images/math/32271058238e6eafef1eaea8c8e5b22721febb60.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
I think that Gavana and Jamil are wrong on this function. In both sources the x[1] term is not squared. As such there will be a minimum at the smallest value of x[1].
Bukin04 objective function.
The Bukin04 global optimization problem is a multimodal minimization problem defined as follows:
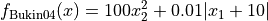
with ![x_1\in [-15, -5], x_2\in [-3, 3]](_images/math/6a2089f48bedd800a6dff64a97d2e3a7459626fa.png)
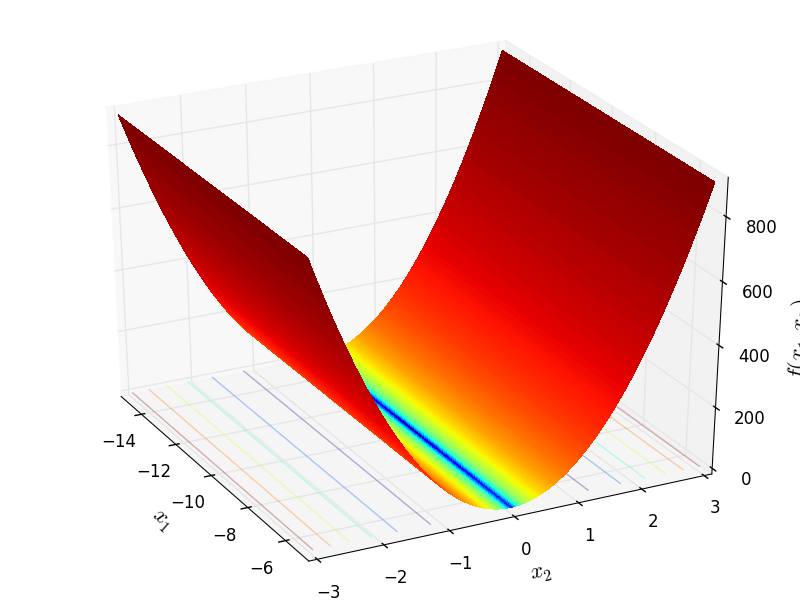
Two-dimensional Bukin04 function
Global optimum:  for
for ![x = [-10, 0]](_images/math/b86a6bab7cb2bc86674e0a0fbafd7eeca4b6dd8f.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Bukin06 objective function.
The Bukin06 global optimization problem is a multimodal minimization problem defined as follows:
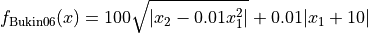
with ![x_1\in [-15, -5], x_2\in [-3, 3]](_images/math/6a2089f48bedd800a6dff64a97d2e3a7459626fa.png)
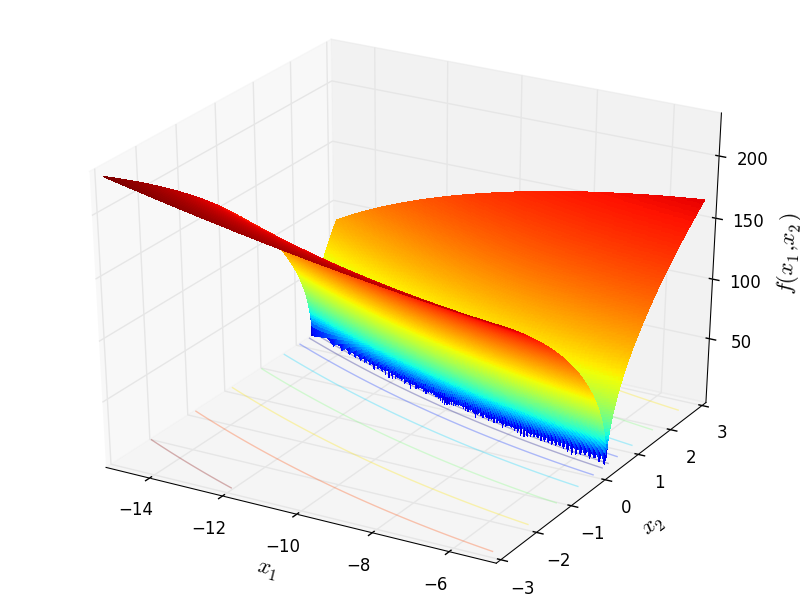
Two-dimensional Bukin06 function
Global optimum:  for
for ![x = [-10, 1]](_images/math/99b5be22c2ffa541f4c85df10c2007c94d5ab1fd.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.