Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions C
 N-D Test Functions C¶
N-D Test Functions C¶CarromTable objective function.
The CarromTable global optimization problem is a multimodal minimization problem defined as follows:
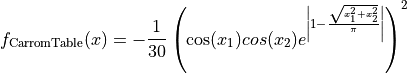
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
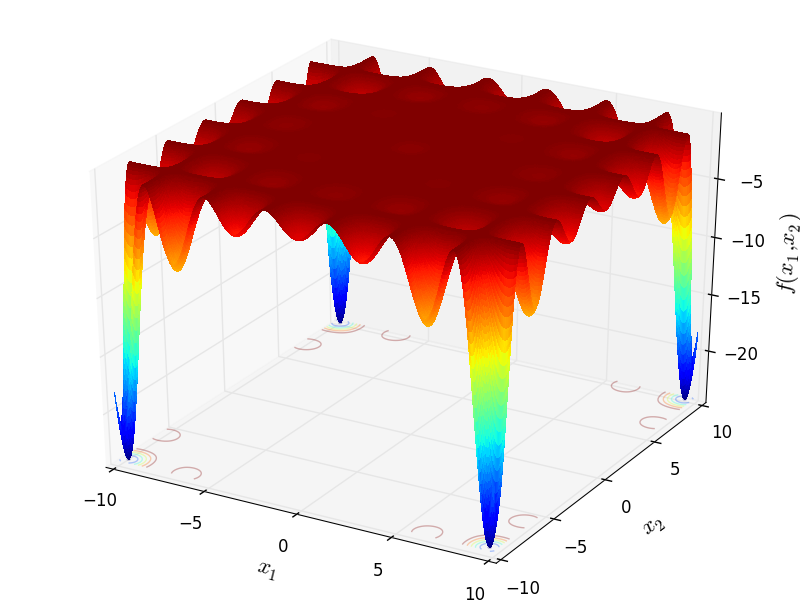
Two-dimensional CarromTable function
Global optimum: 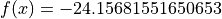 for
for 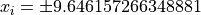 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Chichinadze objective function.
This class defines the Chichinadze global optimization problem. This is a multimodal minimization problem defined as follows:
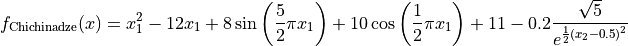
with ![x_i \in [-30, 30]](_images/math/292d5c0e898bdbf6ba6ae08a62a7750af442c17a.png) for
for  .
.
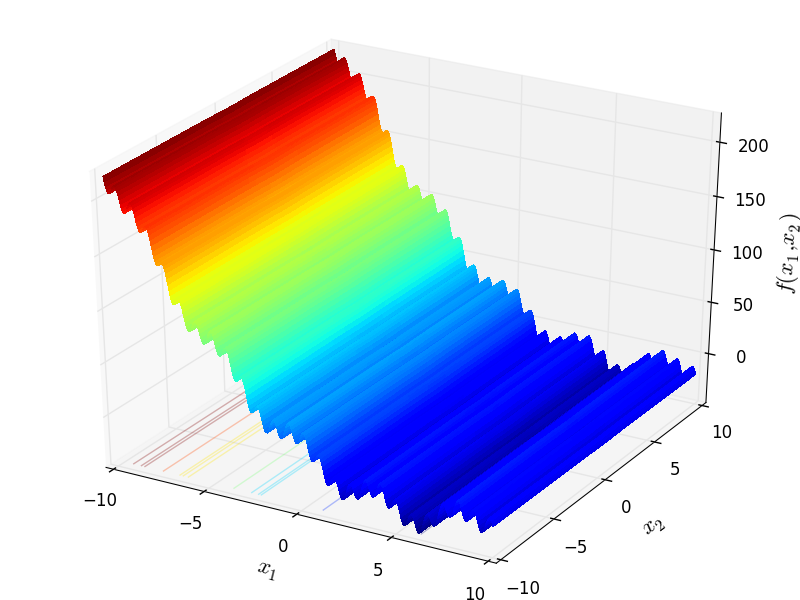
Two-dimensional Chichinadze function
Global optimum: 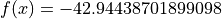 for
for ![x =
[6.189866586965680, 0.5]](_images/math/6017bf20ede3b48893f78f7026de5455275421a5.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil#33 has a dividing factor of 2 in the sin term. However, f(x) for the given solution does not give the global minimum. i.e. the equation is at odds with the solution. Only by removing the dividing factor of 2, i.e. 8 * sin(5 * pi * x[0]) does the given solution result in the given global minimum. Do we keep the result or equation?
Cigar objective function.
This class defines the Cigar global optimization problem. This is a multimodal minimization problem defined as follows:
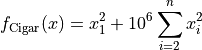
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-100, 100]](_images/math/d8fb57bba3ab0918fa5f82c87dbf208e957d26dc.png) for
for  .
.
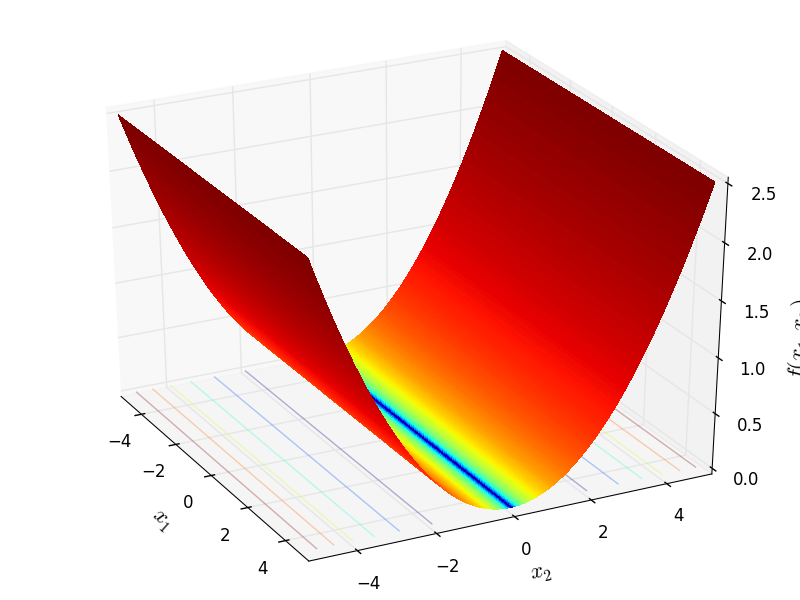
Two-dimensional Cigar function
Global optimum:  for
for 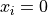 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Cola objective function.
This class defines the Cola global optimization problem. The 17-dimensional
function computes indirectly the formula 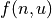 by setting
by setting
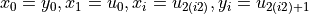 :
:
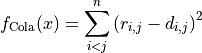
Where 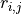 is given by:
is given by:
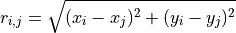
And 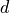 is a symmetric matrix given by:
is a symmetric matrix given by:
![\mathbf{d} = \left [ d_{ij} \right ] = \begin{pmatrix} \\
1.27 & & & & & & & & \\
1.69 & 1.43 & & & & & & & \\
2.04 & 2.35 & 2.43 & & & & & & \\
3.09 & 3.18 & 3.26 & 2.85 & & & & & \\
3.20 & 3.22 & 3.27 & 2.88 & 1.55 & & & & \\
2.86 & 2.56 & 2.58 & 2.59 & 3.12 & 3.06 & & & \\
3.17 & 3.18 & 3.18 & 3.12 & 1.31 & 1.64 & 3.00 & \\
3.21 & 3.18 & 3.18 & 3.17 & 1.70 & 1.36 & 2.95 & 1.32 & \\
2.38 & 2.31 & 2.42 & 1.94 & 2.85 & 2.81 & 2.56 & 2.91 & 2.97
\end{pmatrix}](_images/math/b029a2379e3aa790172b3b6618a60cf657c2617f.png)
This function has bounds ![x_0\in [0, 4]](_images/math/b0fbf620cff527839ba8e025db22eb961483ecb1.png) and
and ![x_i \in [-4, 4]](_images/math/8368ca122c49eafe214d1fd60919e78f69b60fc1.png) for
for  .
Global optimum 11.7464.
.
Global optimum 11.7464.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Colville objective function.
This class defines the Colville global optimization problem. This is a multimodal minimization problem defined as follows:
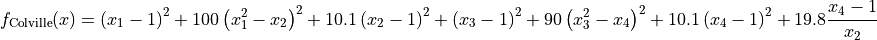
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 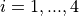 .
.
Global optimum:  for
for 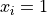 for
for
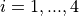
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
docstring equation is wrong use Jamil#36
Corana test objective function.
This class defines the Corana global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Corana}}(x) = \begin{cases} \sum_{i=1}^n 0.15 d_i [z_i - 0.05\textrm{sgn}(z_i)]^2 & \textrm{if }|x_i-z_i| < 0.05 \\
d_ix_i^2 & \textrm{otherwise}\end{cases}](_images/math/77d5fa59fde3127fe3b482fc980594123b8ae5fb.png)
Where, in this exercise:
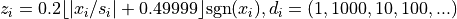
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for 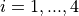 .
.
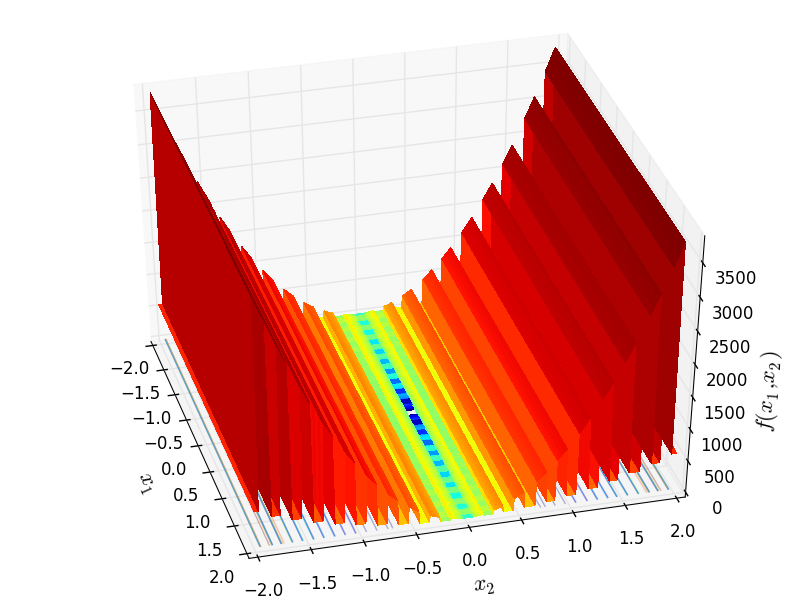
Two-dimensional Corana function
Global optimum: 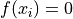 for
for 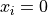 for
for 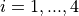
Gavana, A. Global Optimization Benchmarks and AMPGO
Cosine Mixture objective function.
This class defines the Cosine Mixture global optimization problem. This is a multimodal minimization problem defined as follows:
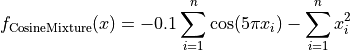
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-1, 1]](_images/math/dde0fc40a453973d1a26279774f867825e6e32ca.png) for
for 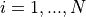 .
.
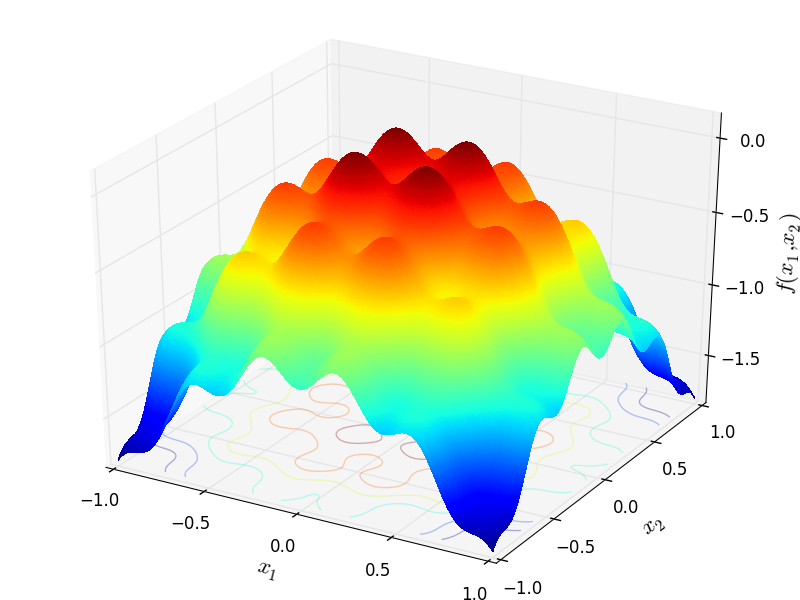
Two-dimensional CosineMixture function
Global optimum: 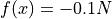 for
for 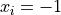 for
for
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil #38 has wrong minimum and wrong fglob. I plotted it. -(x**2) term is always negative if x is negative. cos(5 * pi * x) is equal to -1 for x=-1.
Crescent objective function.
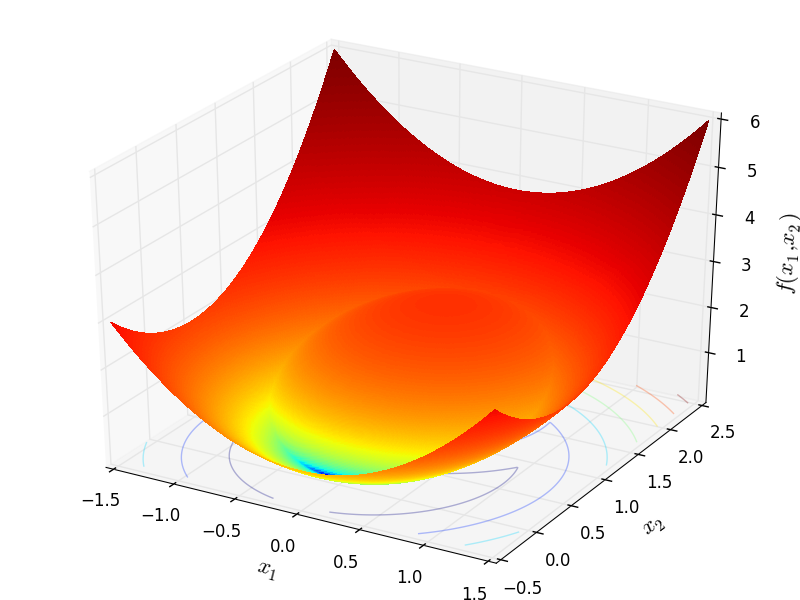
Two-dimensional Crescent function
Cross-in-Tray objective function.
This class defines the Cross-in-Tray global optimization problem. This is a multimodal minimization problem defined as follows:
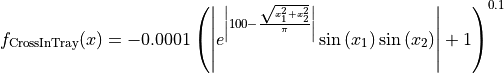
with ![x_i \in [-15, 15]](_images/math/fca9e26666540be67aae472b6068981e5e8b1471.png) for
for  .
.
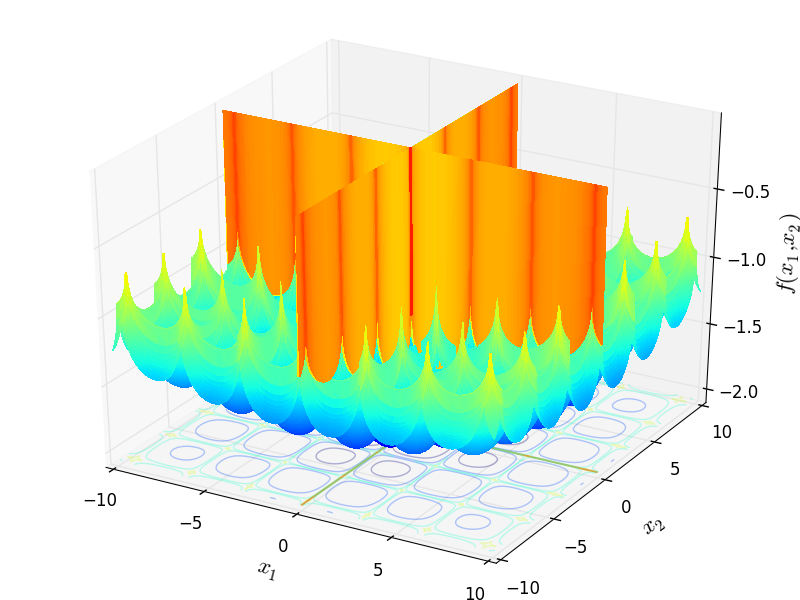
Two-dimensional CrossInTray function
Global optimum: 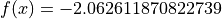 for
for 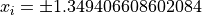 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Cross-Leg-Table objective function.
This class defines the Cross-Leg-Table global optimization problem. This is a multimodal minimization problem defined as follows:
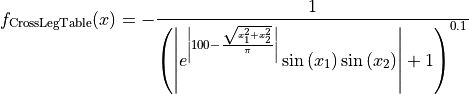
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
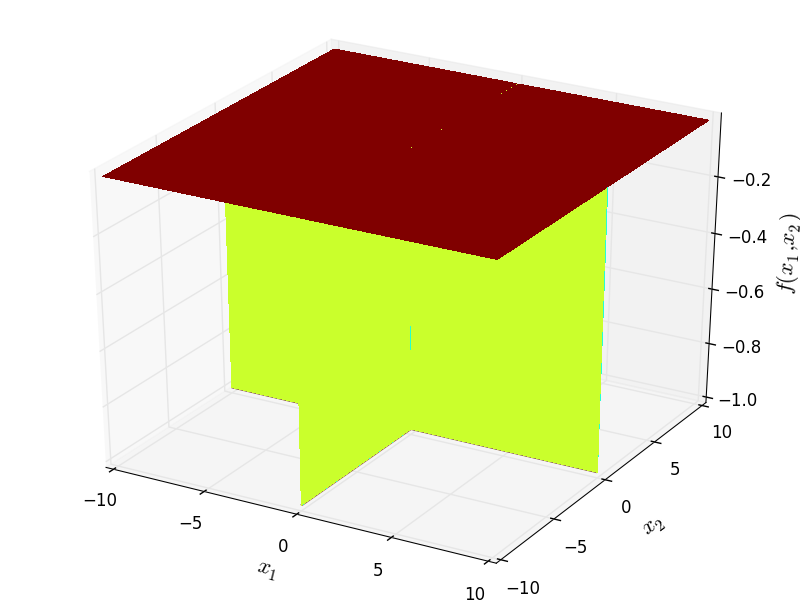
Two-dimensional CrossLegTable function
Global optimum:  . The global minimum is found on the
planes
. The global minimum is found on the
planes 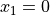 and
and 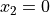
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions Munich University, 2006
Crowned Cross objective function.
This class defines the Crowned Cross global optimization problem. This is a multimodal minimization problem defined as follows:
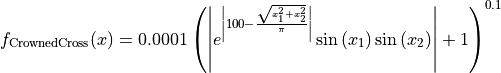
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
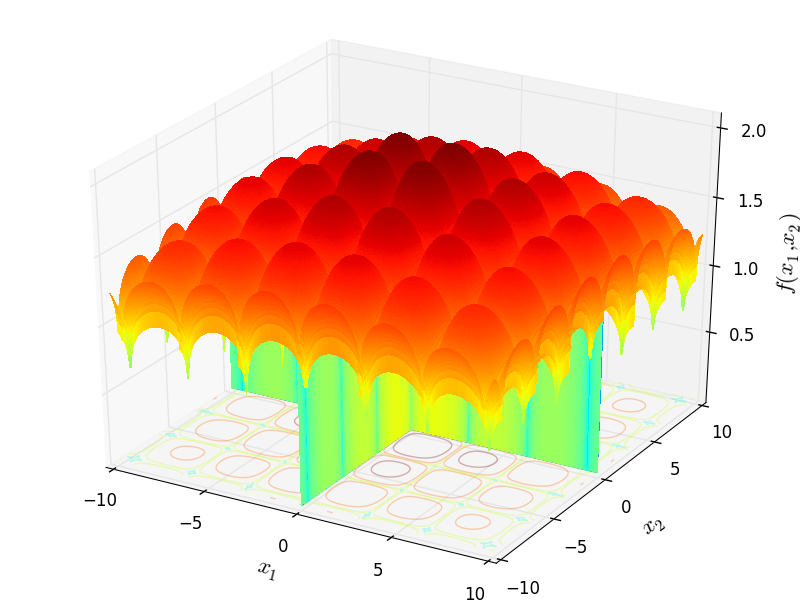
Two-dimensional CrownedCross function
Global optimum: 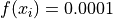 . The global minimum is found on
the planes
. The global minimum is found on
the planes 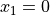 and
and 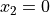
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions Munich University, 2006
Csendes objective function.
This class defines the Csendes global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Csendes}}(x) = \sum_{i=1}^n x_i^6 \left[ 2 + \sin
\left( \frac{1}{x_i} \right ) \right]](_images/math/436e4dc7f1d35b999f588c8ce397f0a846129fdd.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-1, 1]](_images/math/dde0fc40a453973d1a26279774f867825e6e32ca.png) for
for 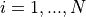 .
.
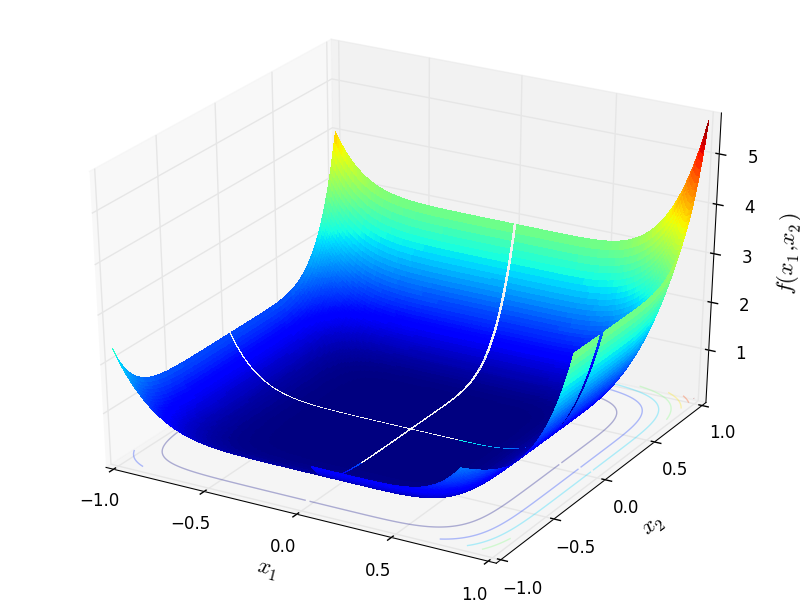
Two-dimensional Csendes function
Global optimum:  for
for 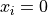 for
for
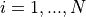
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Cube objective function.
This class defines the Cube global optimization problem. This is a multimodal minimization problem defined as follows:
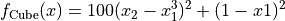
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 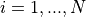 .
.
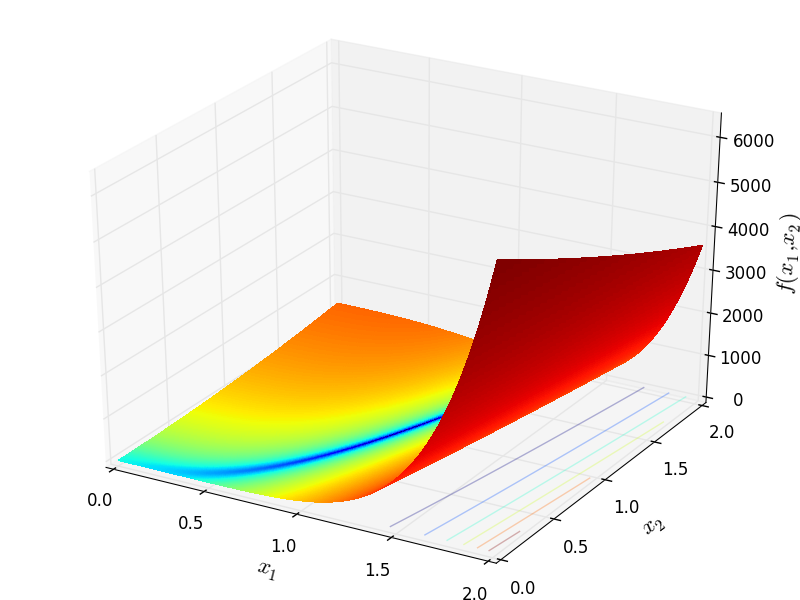
Two-dimensional Cube function
Global optimum: 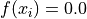 for
for ![x = [1, 1]](_images/math/aca84c9635cb3f5577f7ae4d6f015415a512a7cb.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
jamil#41 has the wrong solution.