 Global Optimization Benchmarks¶
Global Optimization Benchmarks¶This set of HTML pages pretty much superseeds - and greatly expands - the previous analysis that you can find at this location: http://infinity77.net/global_optimization/ .
As far as I can see, no one has ever attempted a benchmark so comprehensive and multi-faceted, although hundreds of papers/websites/tools exist to carry out smaller, simpler benchmarks on Global Optimization algorithms.
The approach I have taken this time is to select as many benchmark test suites as possible: most of them are characterized by test function generators, from which we can actually create almost an unlimited number of unique test problems.
 Introduction¶
Introduction¶These HTML pages contain a series of benchmarks to test a number of numerical Global Optimization algorithms; the algorithms are applied to multi-modal/difficult multi-dimensional test functions. Some of these benchmarks test functions are taken from the literature, but quite a few of them are created with the help of test functions generators.
I have attempted a broad categorization of the benchmarks in The Benchmarks. As a very high level comment, I can anticipate that the whole suite is made up of 6,825 test problems divided across 16 different test suites: most of these problems are of low dimensionality (2 to 6 variables) with a few benchmarks extending to 10+ variables.
 Motivation¶
Motivation¶This effort stems from the fact that I got fed up with the current attitude of most mathematicians/numerical optimization experts, who tend to demonstrate the advantages of an algorithm based on “elapsed time” or “CPU time” or similar meaningless performance indicators.
I deal with real-life optimization problems, as most of us do.
Most real life optimization problems require intensive and time consuming simulations for every function evaluation; the time spent by the solver itself doing its calculations simply disappears in front of the real process simulation. I know it because our simulations take between 2 and 48 hours to run, so what’s 300 seconds more or less in the solver calculations?
 The Rules¶
The Rules¶In order to be eligible for the competition, a Global Optimization algorithm must satisfy the following constraints:
It should run on my PCs, equipped with Windows 10 64 bit and Python 2.7 64 bit. This means that the algorithm should be coded in pure Python, or the developer should provide a Windows installer, or it should be of easy compilation using standard Python tools plus Visual Studio/MinGW64, Intel Fortran/gfortran and f2py.
See The Great Excluded section for a few examples of algorithms written by people living in their dream world.
No unconstrained optimization routines allowed: I mostly care about box-bounded problems, so the algorithm should support bounds on independent variables as a minimum condition for eligibility.
The test suite is executed in the following manner:
Every optimization algorithm is fed with all the test functions:
For the SciPy Extended benchmark, 100 different random starting points are used. For any test function, the starting point is the same for all the algorithms. Please see the description of the SciPy Extended benchmark as it has been havily modified compared to the one in the SciPy distribution.
Benchmark repeatability is enforced through the use of the same random seed every time the test suite is run.
For the NIST benchmark, solvers that accept an initial starting point are fed with the start point number 1 as suggested by NIST. This is not exactly 100% fair to solvers that do not accept an initial guess (DE, MCS, LeapFrog, PSWARM, SHGO), but life is tough.
For all other benchmark suites, only one initial starting point is provided, randomly generated in the function domain. For any test function, the starting point is the same for all the algorithms. This is not exactly 100% fair to solvers that are forced to use an initial guess (AMPGO, BasinHopping, BiteOpt, CMA-ES, CRS2, DIRECT, DualAnnealing, SCE), but life is tough.
Benchmark repeatability is enforced through the use of the same random seed every time the test suite is run.
Please see the The Benchmarks section and all the sub-sequent pages for a more in-depth explanation of the various benchmarks and the results.
No tuning of parameters is allowed: all the algorithms have been run with their default settings, irrespective of the dimensionality of the problem, the starting point or any other consideration.
I am now less fixated with the maximum number of function evaluations, but all benchmark suites have been run repeatedly, by increasing the available budget of function evaluations each time, with 100, 200, 300, ..., 1900, 2000, 5000, 10000 as hard limits.
During each of tose runs, if the assigned limit is exceeded, the test is considered as “failed”. Otherwise the number of function evaluations reported by the algorithm is recorded for later statistical analysis.
All the test functions on almost all benchmark suites have known global optimum values: in the few cases where the global optimum value is unknown (or I was unable to calculate it via analysis) their value has been estimated by enormous grid searches plus repeated minimizations. I then considered an algorithm to be successful if:
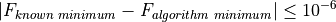
While still respecting the condition at point (2). All the other checks for tolerances - be those on relative change on the objective function from one iteration to the other, or too small variations in the variables in the function domain - have been disabled or mercilessly and brutally commented out in the code for each solver.
 The Great Excluded¶
The Great Excluded¶This section presents a (possibly incomplete) list of algorithms/libraries that have been excluded from the benchmark competition, as they do not comply with one or more of the rules spelled out in The Rules section.
ALGENCAN: praised by many for its robustness and convergence qualities, you can get a copy of the source code from here:
http://www.ime.usp.br/~egbirgin/tango/codes.php
Unfortunately, no Windows installer is available and the code is not easily compilable on Windows.
Fail.
PyGMO: based on the C++ code of PaGMO, it contains a lot of different optimizers and seems very promising:
http://pagmo.sourceforge.net/pygmo/index.html
Unfortunately, the Windows version is 32 bit-only, and compilation seems to be a very problematic matter.
Fail.
 Tested Algorithms¶
Tested Algorithms¶I have tried a number of global optimization algorithms on the entire set of benchmarks, considering bound constrained problems only, and specifically the following ones:
AMPGO: Adaptive Memory Programming for Global Optimization: this is my Python implementation of the algorithm described here:
I have added a few improvements here and there based on my Master Thesis work on the standard Tunnelling Algorithm of Levy, Montalvo and Gomez. After AMPGO was integrated in lmfit, I have improved it even more - in my opinion.
BasinHopping: Basin hopping is a random algorithm which attempts to find the global minimum of a smooth scalar function of one or more variables. The algorithm was originally described by David Wales:
http://www-wales.ch.cam.ac.uk/
BasinHopping is now part of the standard SciPy distribution.
BiteOpt: BITmask Evolution OPTimization, based on the algorithm presented in this GitHub link:
https://github.com/avaneev/biteopt
I have converted the C++ code into Python and added a few, minor modifications.
CMA-ES: Covariance Matrix Adaptation Evolution Strategy, based on the following algorithm:
http://www.lri.fr/~hansen/cmaesintro.html
http://www.lri.fr/~hansen/cmaes_inmatlab.html#python (Python code for the algorithm)
CRS2: Controlled Random Search with Local Mutation, as implemented in the NLOpt package:
DE: Differential Evolution, described in the following page:
http://www1.icsi.berkeley.edu/~storn/code.html
DE is now part of the standard SciPy distribution, and I have taken the implementation as it stands in SciPy:
DIRECT: the DIviding RECTangles procedure, described in:
http://ab-initio.mit.edu/wiki/index.php/NLopt_Algorithms#DIRECT_and_DIRECT-L (Python code for the algorithm)
DualAnnealing: the Dual Annealing algorithm, taken directly from the SciPy implementation:
LeapFrog: the Leap Frog procedure, which I have been recommended for use, taken from:
MCS: Multilevel Coordinate Search, it’s my translation to Python of the original Matlab code from A. Neumaier and W. Huyer (giving then for free also GLS and MINQ):
https://www.mat.univie.ac.at/~neum/software/mcs/
I have added a few, minor improvements compared to the original implementation. See the MCS section for a quick and dirty comparison between the Matlab code and my Python conversion.
PSWARM: Particle Swarm optimization algorithm, it has been described in many online papers. I have used a compiled version of the C source code from:
SCE: Shuffled Complex Evolution, described in:
Duan, Q., S. Sorooshian, and V. Gupta, Effective and efficient global optimization for conceptual rainfall-runoff models, Water Resour. Res., 28, 1015-1031, 1992.
The version I used was graciously made available by Matthias Cuntz via a personal e-mail.
SHGO: Simplicial Homology Global Optimization, taken directly from the SciPy implementation:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.shgo.html#scipy.optimize.shgo
Note
Please feel free to contact me if you think I have missed one (or more) algorithm/library, or if you have a procedure you would like to benchmark against. Do send me an email to andrea.gavana@gmail.com, I’ll integrate your contribution with due credits and I will re-run the algorithms comparison.
 Indices and tables¶
Indices and tables¶