Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions D
 N-D Test Functions D¶
N-D Test Functions D¶Damavandi objective function.
This class defines the Damavandi global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Damavandi}}(x) = \left[ 1 - \lvert{\frac{
\sin[\pi (x_1 - 2)]\sin[\pi (x2 - 2)]}{\pi^2 (x_1 - 2)(x_2 - 2)}}
\rvert^5 \right] \left[2 + (x_1 - 7)^2 + 2(x_2 - 7)^2 \right]](_images/math/c0c3b99134a5ee04772924c498f14fab9cd647c0.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[0, 14]](_images/math/65948ec215db017df2d54cc9af1db05c2ad9fd2a.png) for
for  .
.
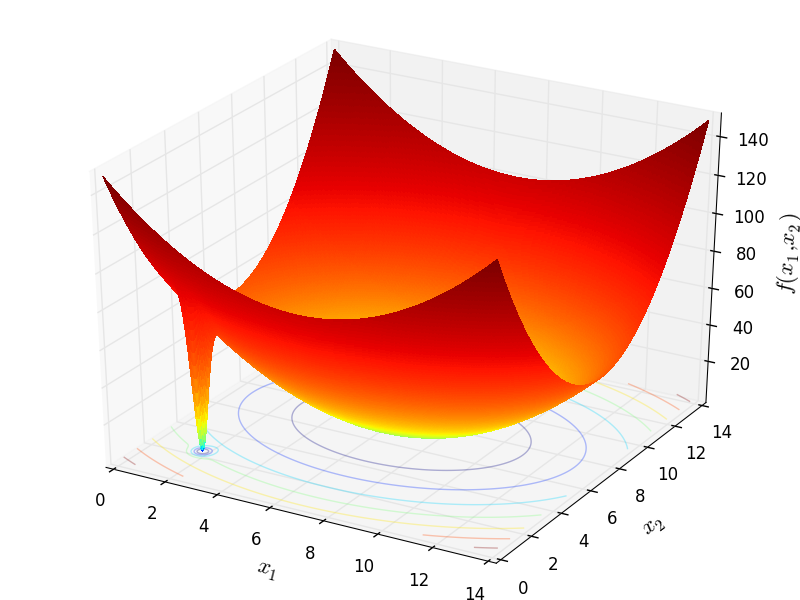
Two-dimensional Damavandi function
Global optimum:  for
for 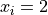 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Deb 1 objective function.
This class defines the Deb 1 global optimization problem. This is a multimodal minimization problem defined as follows:
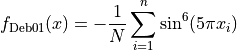
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
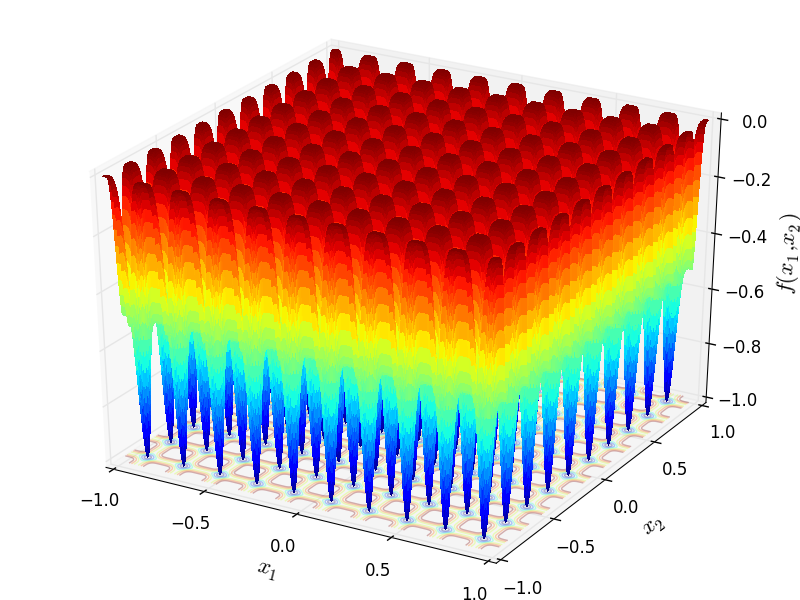
Two-dimensional Deb01 function
Global optimum: 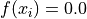 . The number of global minima is
. The number of global minima is
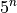 that are evenly spaced in the function landscape, where
that are evenly spaced in the function landscape, where
 represents the dimension of the problem.
represents the dimension of the problem.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Deb 3 objective function.
This class defines the Deb 3 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Deb03}}(x) = - \frac{1}{N} \sum_{i=1}^n \sin^6 \left[ 5 \pi
\left ( x_i^{3/4} - 0.05 \right) \right ]](_images/math/cb1d4582278ba34a8124cd88351553464c1ea94d.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[0, 1]](_images/math/dfa822989440dd5189a02d6f01863aa6eba78428.png) for
for  .
.
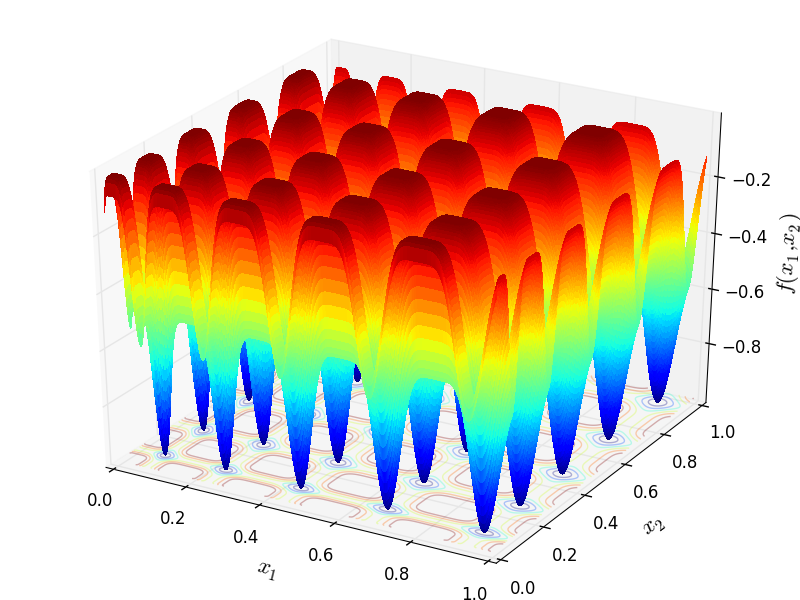
Two-dimensional Deb03 function
Global optimum:  . The number of global minima is
. The number of global minima is
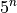 that are evenly spaced in the function landscape, where
that are evenly spaced in the function landscape, where
 represents the dimension of the problem.
represents the dimension of the problem.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Decanomial objective function.
This class defines the Decanomial function global optimization problem. This is a multimodal minimization problem defined as follows:
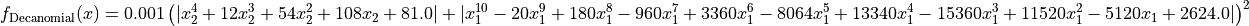
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
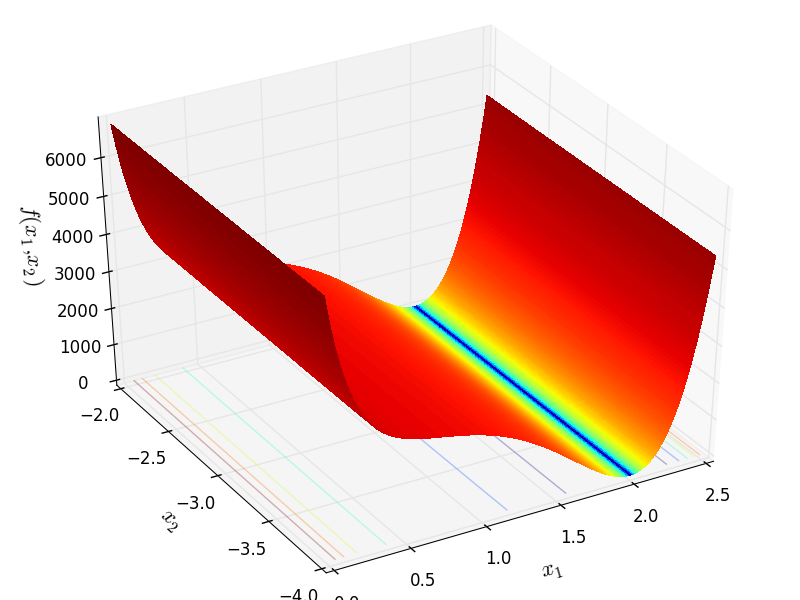
Two-dimensional Decanomial function
Global optimum:  for
for ![x = [2, -3]](_images/math/2570e1e7f0a7fb488cffbaae74b24e543db426a7.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Deceptive objective function.
This class defines the Deceptive global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Deceptive}}(x) = - \left [\frac{1}{n}
\sum_{i=1}^{n} g_i(x_i) \right ]^{\beta}](_images/math/b2fffc4c73a67b70a989ea5bb115959dc85e2af8.png)
Where 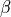 is a fixed non-linearity factor; in this exercise,
is a fixed non-linearity factor; in this exercise,
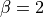 . The function
. The function 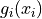 is given by:
is given by:
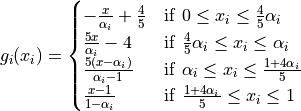
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[0, 1]](_images/math/dfa822989440dd5189a02d6f01863aa6eba78428.png) for
for  .
.
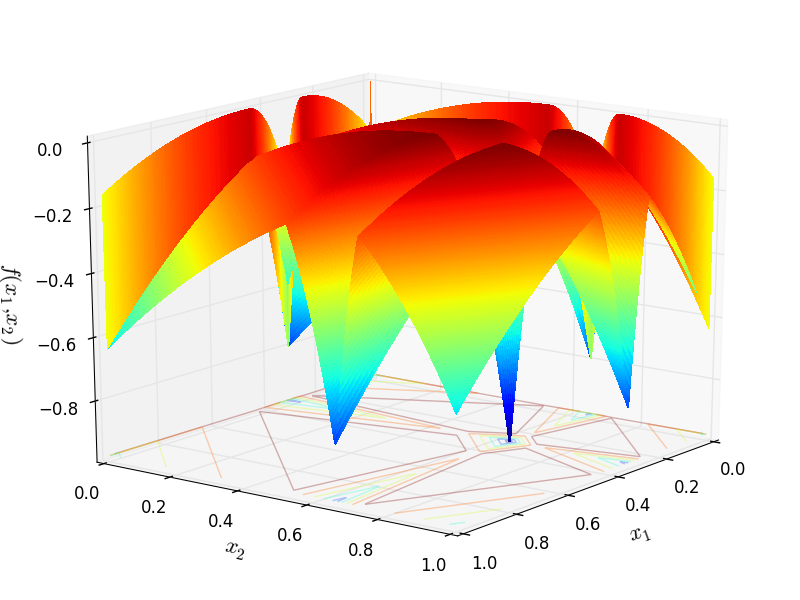
Two-dimensional Deceptive function
Global optimum:  for
for 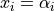 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
this function was taken from the Gavana website. The following code is based on his code. His code and the website don’t match, the equations are wrong.
Deckkers-Aarts objective function.
This class defines the Deckkers-Aarts global optimization problem. This is a multimodal minimization problem defined as follows:
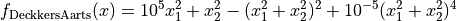
with ![x_i \in [-20, 20]](_images/math/026a917a812dbaef4e7a8ea87e9963bb111e2644.png) for
for  .
.
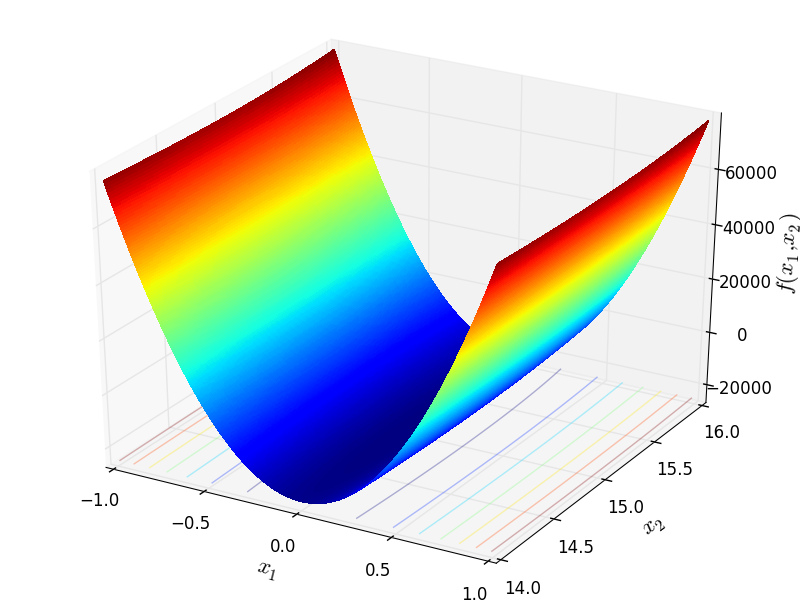
Two-dimensional DeckkersAarts function
Global optimum: 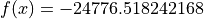 for
for
![x = [0, \pm 14.9451209]](_images/math/d6834a4979ea79a051672648db8ceebf9e5556a1.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
jamil solution and global minimum are slightly wrong.
DeflectedCorrugatedSpring objective function.
This class defines the Deflected Corrugated Spring function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeflectedCorrugatedSpring}}(x) = 0.1\sum_{i=1}^n \left[ (x_i -
\alpha)^2 - \cos \left( K \sqrt {\sum_{i=1}^n (x_i - \alpha)^2}
\right ) \right ]](_images/math/332390faa311ea6fbc9cd55e6e6e1c312812d0e0.png)
Where, in this exercise, 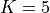 and
and 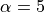 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[0, 2\alpha]](_images/math/75de464b0dd28836589a32c01b9f02c074bca554.png) for
for  .
.
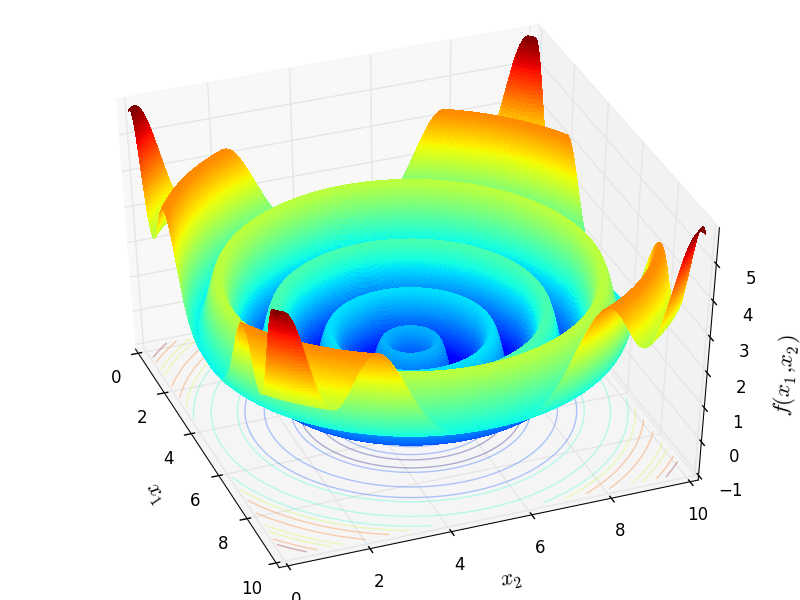
Two-dimensional DeflectedCorrugatedSpring function
Global optimum:  for
for 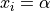 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
website has a different equation to the gavana codebase. The function below is different to the equation above. Also, the global minimum is wrong.
De Jong Function No. 5
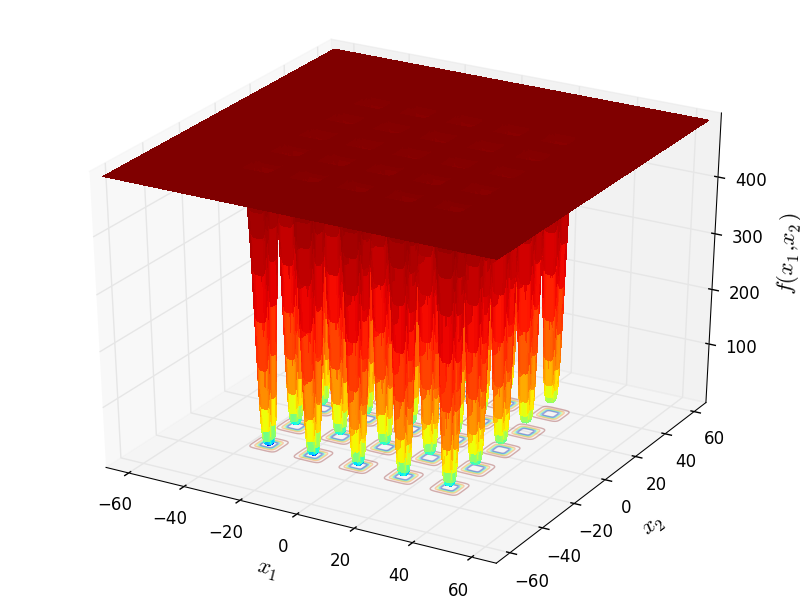
Two-dimensional DeJong5 function
DeVilliers-Glasser 1 objective function.
This class defines the DeVilliers-Glasser 1 function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeVilliersGlasser01}}(x) = \sum_{i=1}^{24} \left[ x_1x_2^{t_i}
\sin(x_3t_i + x_4) - y_i \right ]^2](_images/math/6462aebfe876f38b1043bc1f1d3520b50e6cb9b6.png)
Where, in this exercise, 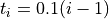 and
and
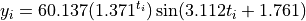 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[1, 100]](_images/math/8a2740157669bedc0551cc95797694f94b6147f5.png) for
for 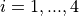 .
.
Global optimum:  for
for 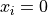 for
for
![x = [60.137, 1.371, 3.112, 1.761]](_images/math/d17c3aa938e9b374248f159581ab28bdb8139efe.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
DeVilliers-Glasser 2 objective function.
This class defines the DeVilliers-Glasser 2 function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeVilliersGlasser01}}(x) = \sum_{i=1}^{24} \left[ x_1x_2^{t_i}
\tanh \left [x_3t_i + \sin(x_4t_i) \right] \cos(t_ie^{x_5}) -
y_i \right ]^2](_images/math/9b7c6b9fb24e1d2348803db3a174b844189c6e08.png)
Where, in this exercise, 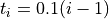 and
and
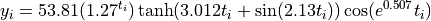 .
.
with ![x_i \in [0.5, 60]](_images/math/c22b44872ce1e5a3aa50e749fc25508d0e957399.png) for
for 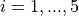 .
.
Global optimum:  for
for
![x = [53.81, 1.27, 3.012, 2.13, 0.507]](_images/math/c505f8ef80c2686ea93991514ba5ffc3c25a6799.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Dixon and Price objective function.
This class defines the Dixon and Price global optimization problem. This is a multimodal minimization problem defined as follows:
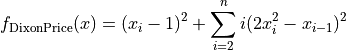
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
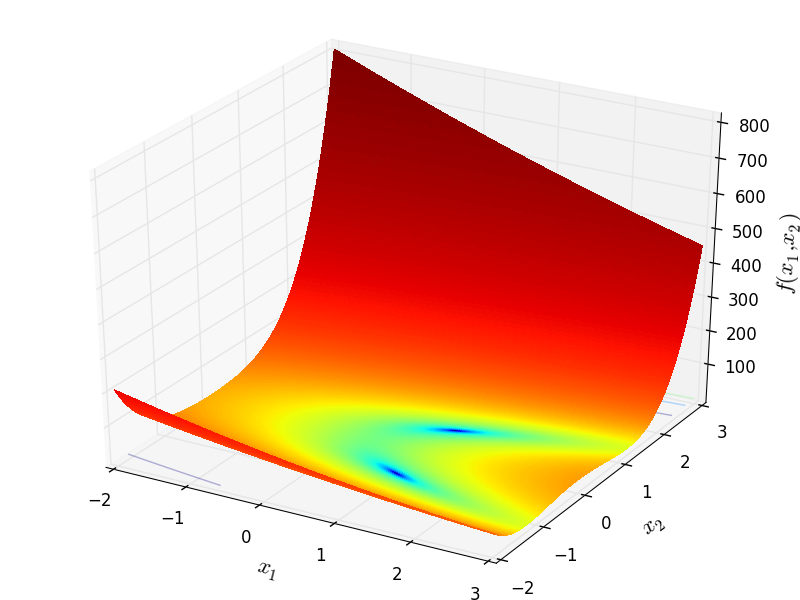
Two-dimensional DixonPrice function
Global optimum: 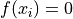 for
for
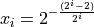 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Gavana code not correct. i array should start from 2.
Dolan objective function.
This class defines the Dolan global optimization problem. This is a multimodal minimization problem defined as follows:
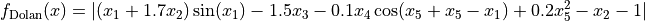
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for 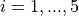 .
.
Global optimum: 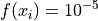 for
for
![x = [8.39045925, 4.81424707, 7.34574133, 68.88246895, 3.85470806]](_images/math/152ecc549af92bc466d149f0d4db7464b9d28e49.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
DropWave objective function.
This class defines the DropWave global optimization problem. This is a multimodal minimization problem defined as follows:
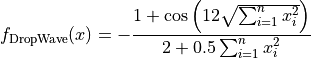
with ![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.
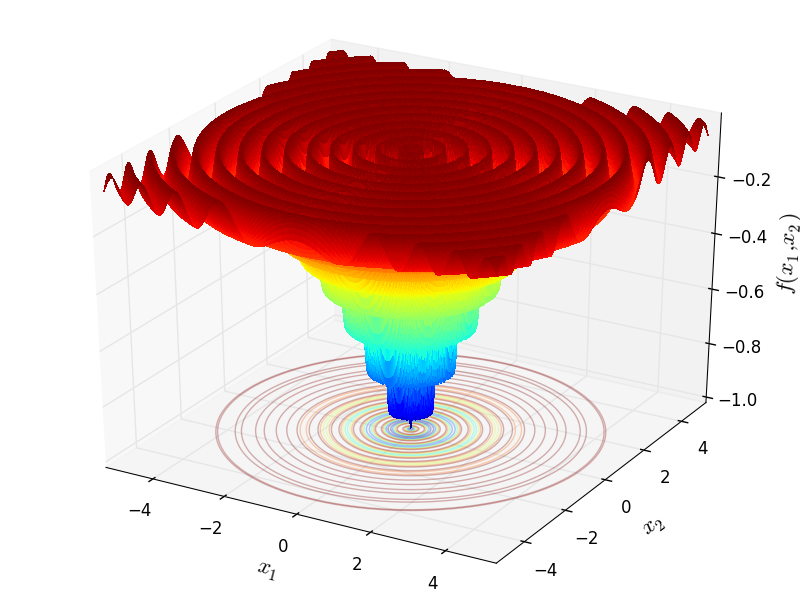
Two-dimensional DropWave function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Gavana, A. Global Optimization Benchmarks and AMPGO