Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions E
 N-D Test Functions E¶
N-D Test Functions E¶Easom objective function.
This class defines the Easom global optimization problem. This is a a multimodal minimization problem defined as follows:
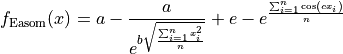
Where, in this exercise, 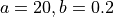 and
and  .
.
Here, ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
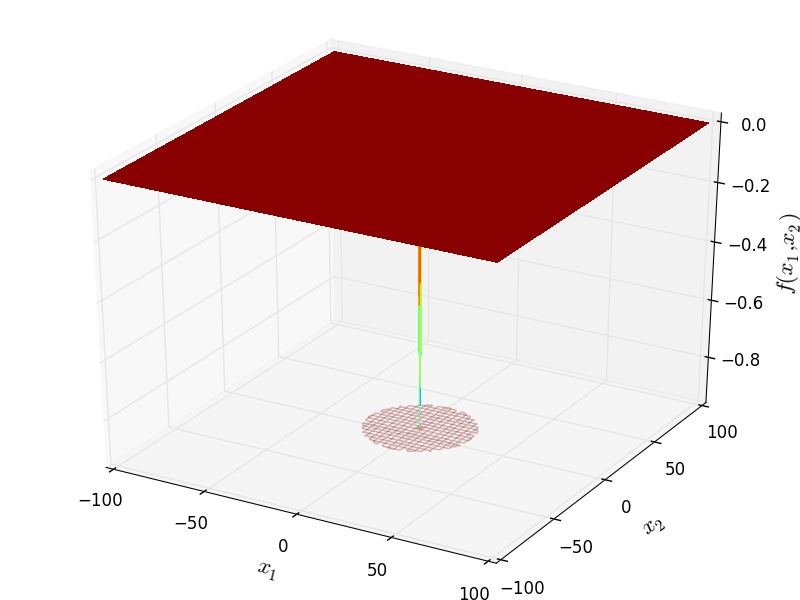
Two-dimensional Easom function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Eckerle4 objective function. Eckerle, K., NIST (1979). Circular Interference Transmittance Study.
Egg Crate objective function.
This class defines the Egg Crate global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{EggCrate}}(x) = x_1^2 + x_2^2 + 25 \left[ \sin^2(x_1)
+ \sin^2(x_2) \right]](_images/math/821d74cc4fcb418405634a56c209f52e4d44867e.png)
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
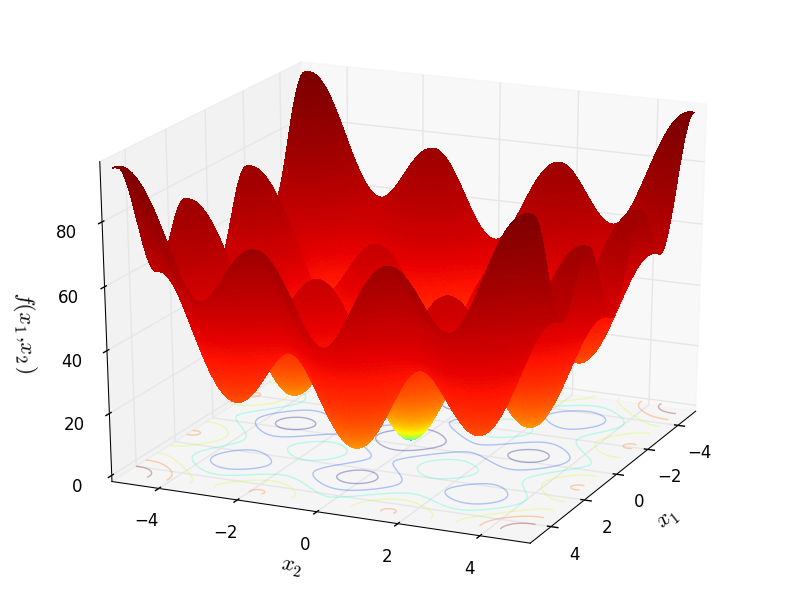
Two-dimensional EggCrate function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Egg Holder objective function.
This class defines the Egg Holder global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{EggHolder}}=\sum_{1}^{n - 1}\left[-\left(x_{i + 1}
+ 47 \right ) \sin\sqrt{\lvert x_{i+1} + x_i/2 + 47 \rvert}
- x_i \sin\sqrt{\lvert x_i - (x_{i + 1} + 47)\rvert}\right ]](_images/math/a0c7559ee85dbc2af31d6a191921c552712ab47b.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-512, 512]](_images/math/a6d22c58aeac9cb8da9f563421b93af44000be24.png) for
for  .
.
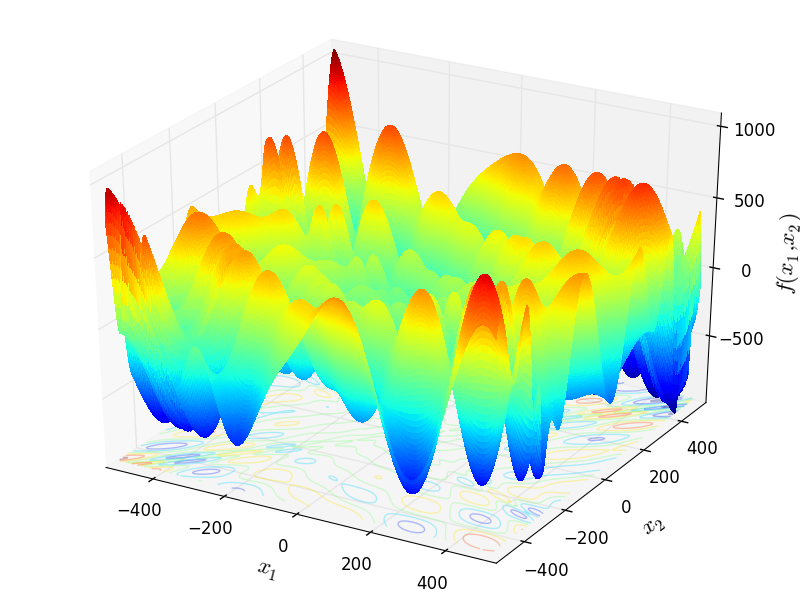
Two-dimensional EggHolder function
Global optimum: 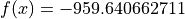 for
for
![{x} = [512, 404.2319]](_images/math/dc5654c889263700d0a90b3c001e6f2ed613a53a.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil is missing a minus sign on the fglob value
El-Attar-Vidyasagar-Dutta objective function.
This class defines the El-Attar-Vidyasagar-Dutta function global optimization problem. This is a multimodal minimization problem defined as follows:
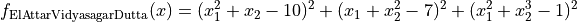
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
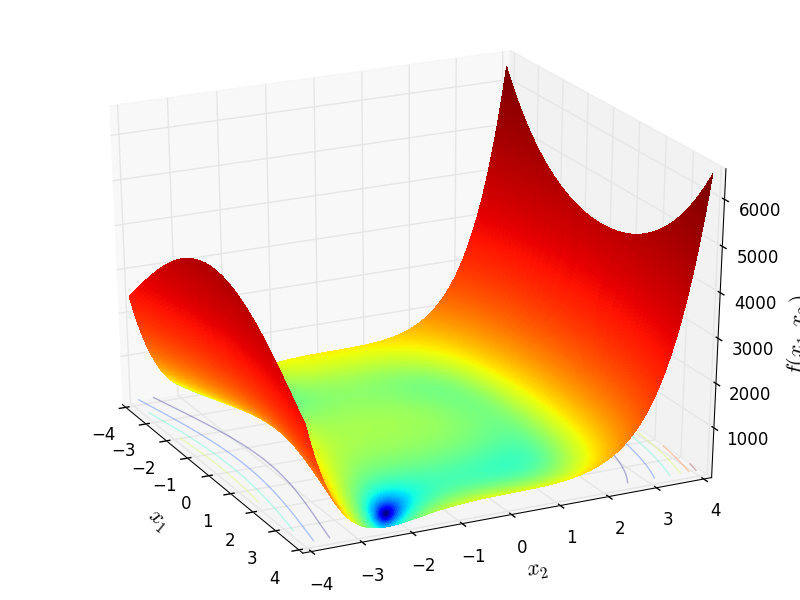
Two-dimensional ElAttarVidyasagarDutta function
Global optimum: 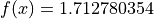 for
for
![x= [3.40918683, -2.17143304]](_images/math/b5f247d45b2bef2bc011a82015f59e85853c2f5b.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Engvall objective function.
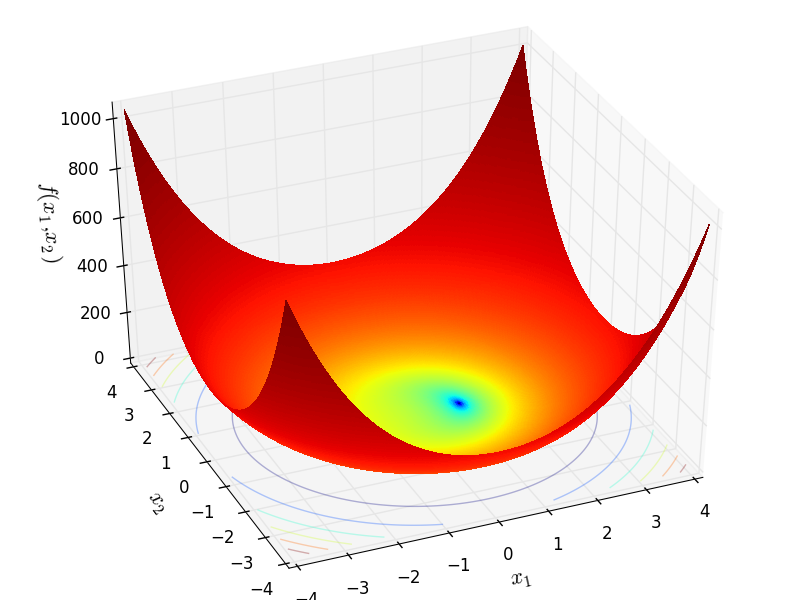
Two-dimensional Engvall function
Exp2 objective function.
This class defines the Exp2 global optimization problem. This is a multimodal minimization problem defined as follows:
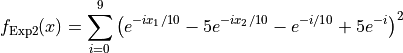
with ![x_i \in [0, 20]](_images/math/e5cccc28ef66f0ce2a2510a87fb96ecd83484bd5.png) for
for  .
.
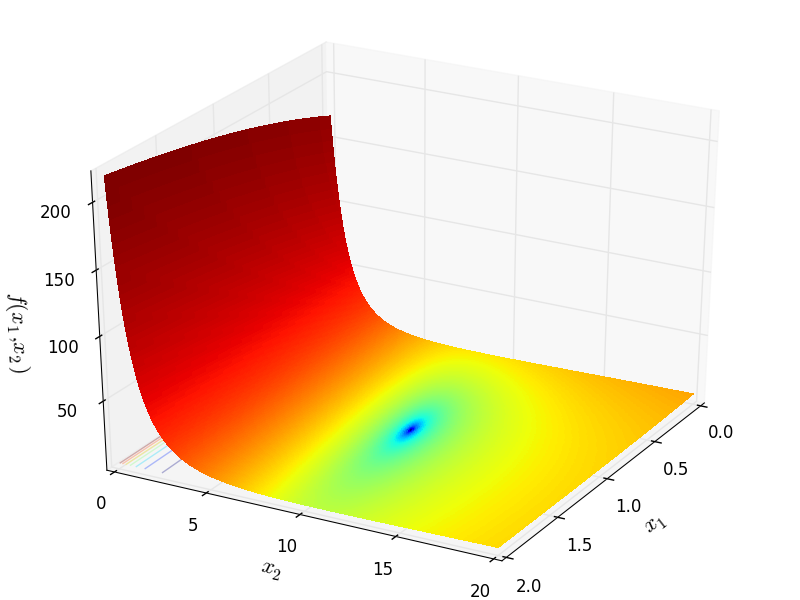
Two-dimensional Exp2 function
Global optimum:  for
for ![x = [1, 10.]](_images/math/6e9fccd5ef86fe03d7b2a6510ab081d9e02936bf.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Exponential [1] objective function.
This class defines the Exponential global optimization problem. This is a multimodal minimization problem defined as follows:
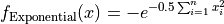
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-1, 1]](_images/math/dde0fc40a453973d1a26279774f867825e6e32ca.png) for
for  .
.
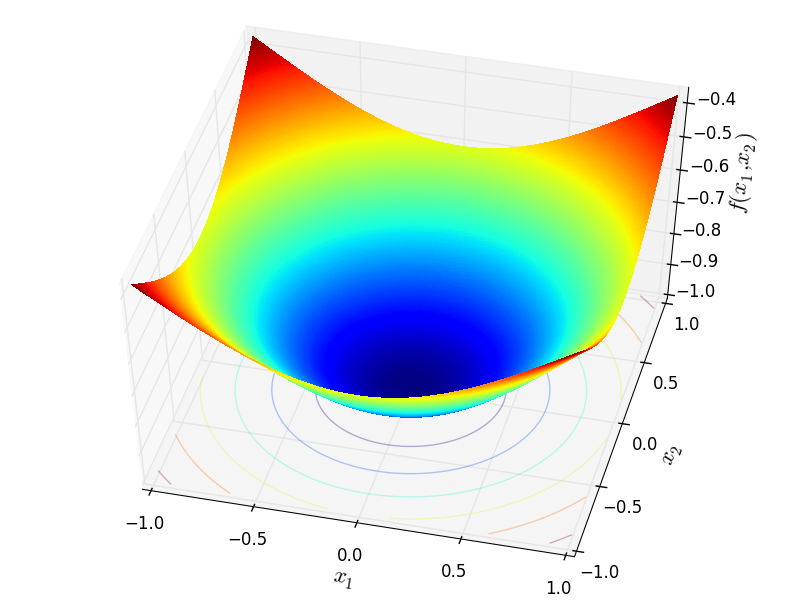
Two-dimensional Exponential function
Global optimum: 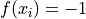 for
for 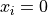 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil are missing a minus sign on fglob