Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions M
 N-D Test Functions M¶
N-D Test Functions M¶Matyas objective function.
This class defines the Matyas global optimization problem. This is a multimodal minimization problem defined as follows:
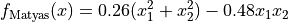
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
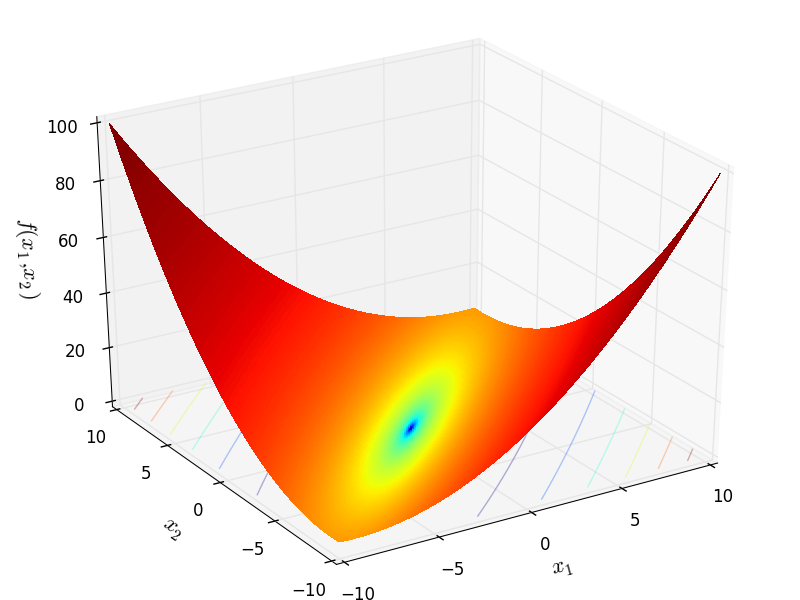
Two-dimensional Matyas function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
McCormick objective function.
This class defines the McCormick global optimization problem. This is a multimodal minimization problem defined as follows:
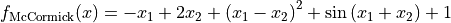
with ![x_1\in [-1.5, 4]](_images/math/7a3a3c1dd20c4df0d3403c2378a2aed39b0ed84e.png) ,
, ![x_2\in [-3, 4]](_images/math/567297853c7fe702c5f73aa7c46ce896b6441ad2.png) .
.
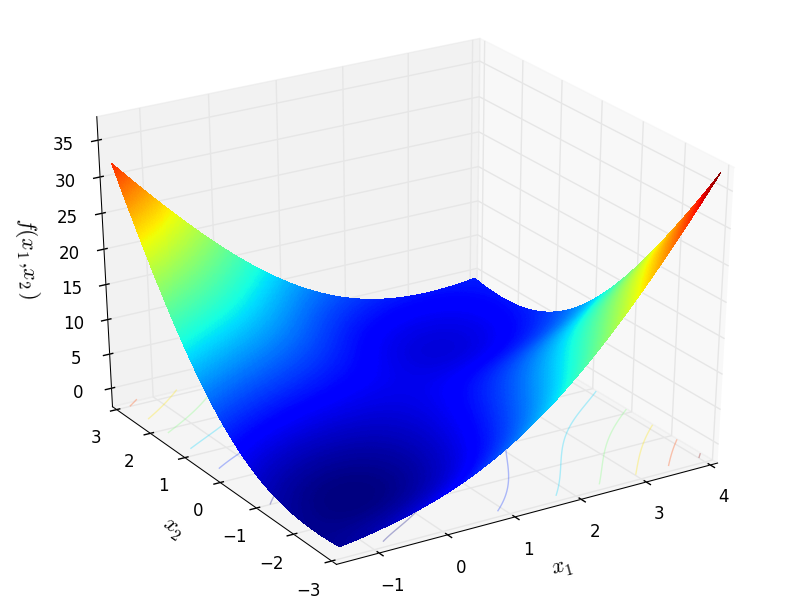
Two-dimensional McCormick function
Global optimum: 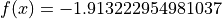 for
for
![x = [-0.5471975602214493, -1.547197559268372]](_images/math/997e56e792f46f6e3592fa37f88016627c8d2a2a.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Meyer objective function.
http://www.itl.nist.gov/div898/strd/nls/data/mgh10.shtml
Todo
NIST regression standard
MeyerRoth objective function.
Michalewicz objective function.
This class defines the Michalewicz global optimization problem. This is a multimodal minimization problem defined as follows:
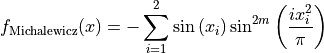
Where, in this exercise, 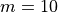 .
.
with ![x_i \in [0, \pi]](_images/math/10b9f829ecf73e20ecc5c80159a1d1615d4c0f6a.png) for
for  .
.
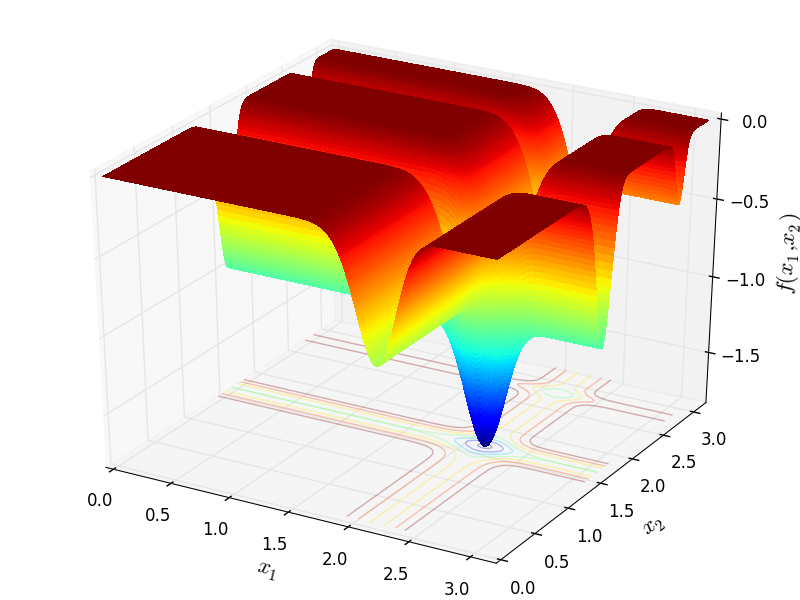
Two-dimensional Michalewicz function
Global optimum: 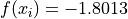 for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Adorio, E. MVF - “Multivariate Test Functions Library in C for Unconstrained Global Optimization”, 2005
Todo
could change dimensionality, but global minimum might change.
Miele-Cantrell objective function.
This class defines the Miele-Cantrell global optimization problem. This is a multimodal minimization problem defined as follows:
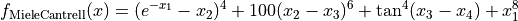
with ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for 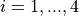 .
.
Global optimum:  for
for ![x = [0, 1, 1, 1]](_images/math/6e3e53931738ccc08c957b15b7a060b6a3ca7554.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Mishra 1 objective function.
This class defines the Mishra 1 global optimization problem. This is a multimodal minimization problem defined as follows:
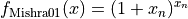
where
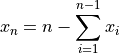
with ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for 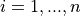 .
.
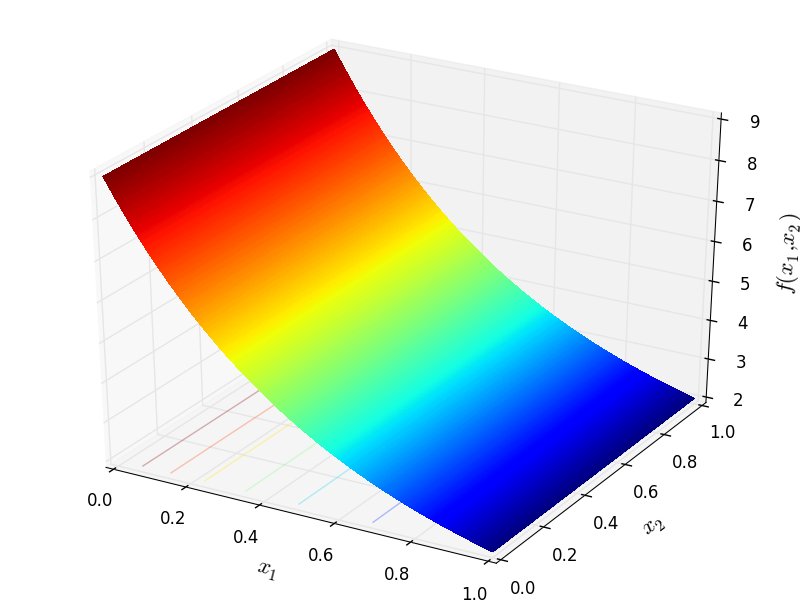
Two-dimensional Mishra01 function
Global optimum: 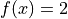 for
for 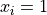 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Mishra 2 objective function.
This class defines the Mishra 2 global optimization problem. This is a multimodal minimization problem defined as follows:
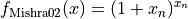
with
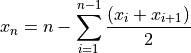
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
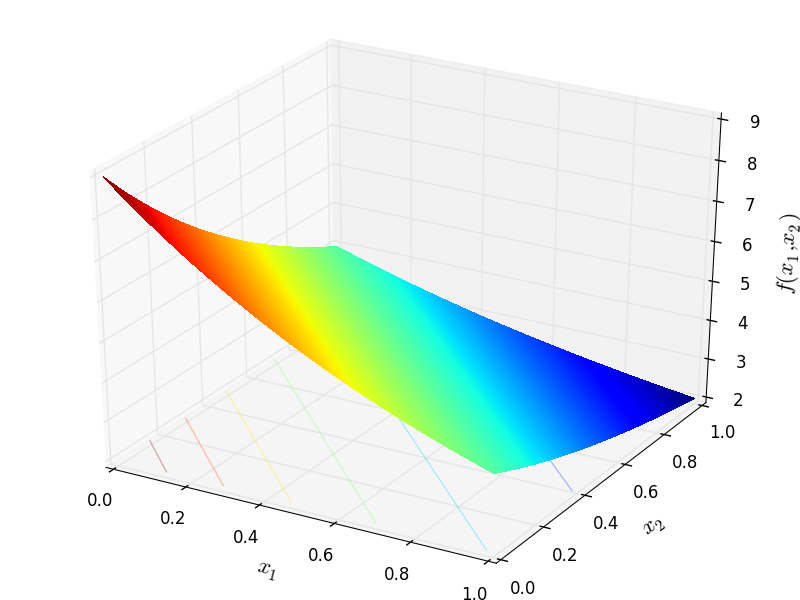
Two-dimensional Mishra02 function
Global optimum: 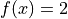 for
for 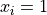 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Mishra 3 objective function.
This class defines the Mishra 3 global optimization problem. This is a multimodal minimization problem defined as follows:
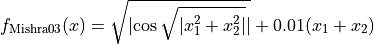
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
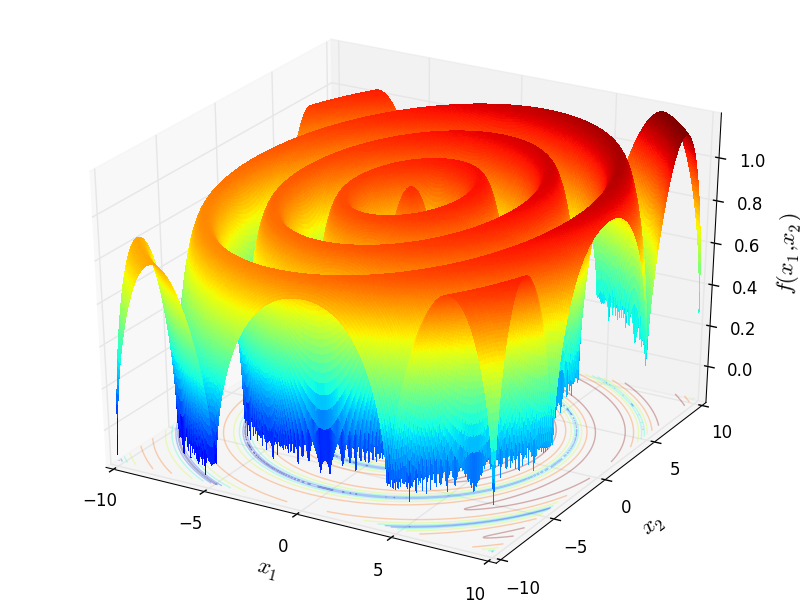
Two-dimensional Mishra03 function
Global optimum: 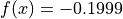 for
for
![x = [-9.99378322, -9.99918927]](_images/math/61970b503593bf3ebf1ce39dd6214b8601c58516.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
I think that Jamil#76 has the wrong global minimum, a smaller one is possible
Mishra 4 objective function.
This class defines the Mishra 4 global optimization problem. This is a multimodal minimization problem defined as follows:
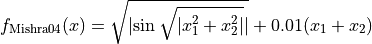
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
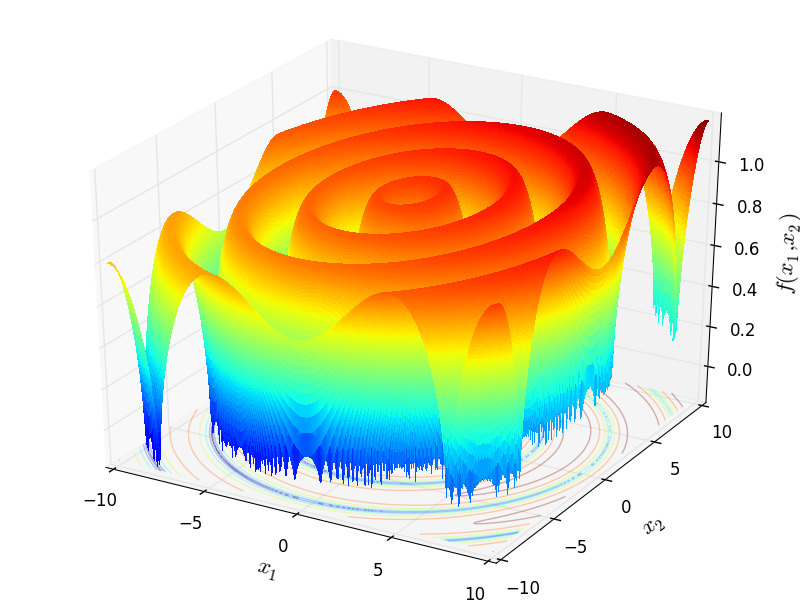
Two-dimensional Mishra04 function
Global optimum: 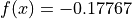 for
for
![x = [-8.71499636, -9.0533148]](_images/math/29f2b9a5d79e2848969cb53e43530f2131f2c6ec.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
I think that Jamil#77 has the wrong minimum, not possible
Mishra 5 objective function.
This class defines the Mishra 5 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra05}}(x) = \left [ \sin^2 ((\cos(x_1) + \cos(x_2))^2)
+ \cos^2 ((\sin(x_1) + \sin(x_2))^2) + x_1 \right ]^2 + 0.01(x_1 + x_2)](_images/math/7b45bd886e9202e85aab18fddbb68bc065b36f52.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
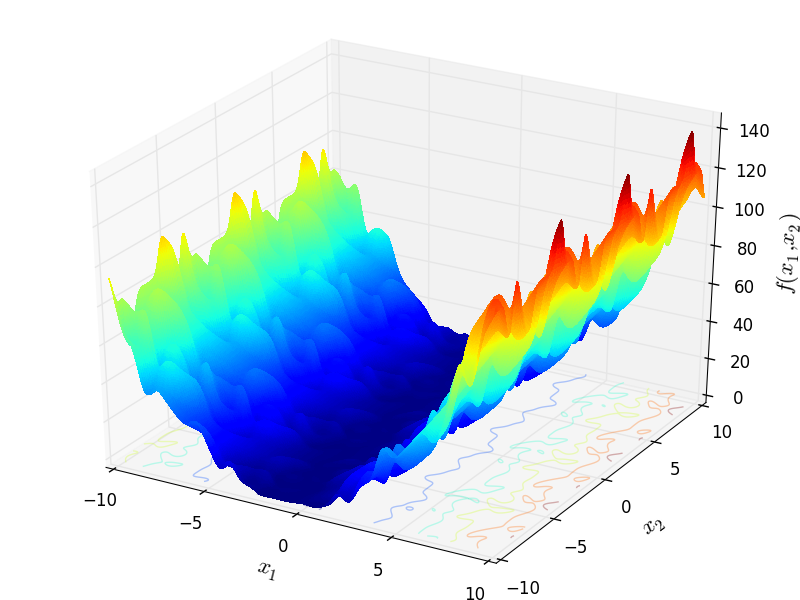
Two-dimensional Mishra05 function
Global optimum: 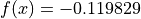 for
for ![x = [-1.98682, -10]](_images/math/10dde29393850a1ae6a13bfbe2753c190bed7802.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
Line 381 in paper
Mishra 6 objective function.
This class defines the Mishra 6 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra06}}(x) = -\log{\left [ \sin^2 ((\cos(x_1)
+ \cos(x_2))^2) - \cos^2 ((\sin(x_1) + \sin(x_2))^2) + x_1 \right ]^2}
+ 0.01 \left[(x_1 -1)^2 + (x_2 - 1)^2 \right]](_images/math/bb5a6b78e0863154a46372db1206fa620a98fbec.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
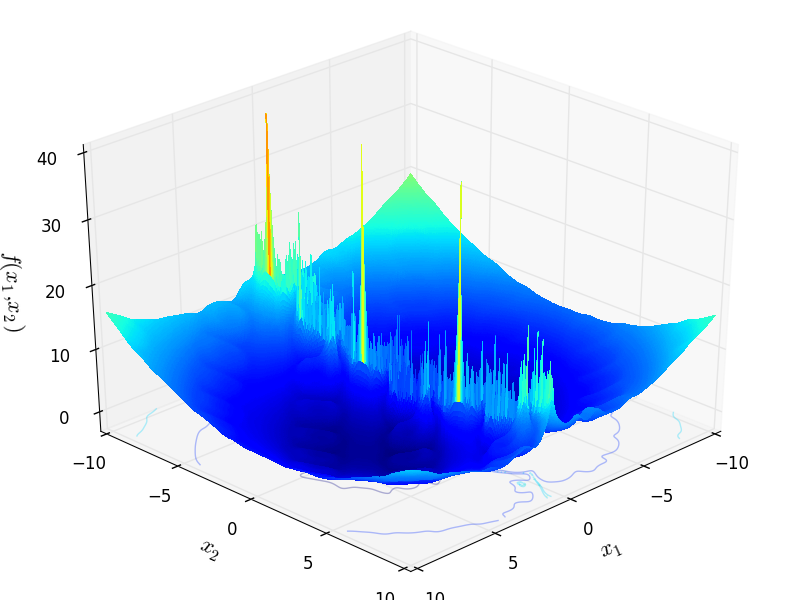
Two-dimensional Mishra06 function
Global optimum: 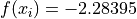 for
for ![x = [2.88631, 1.82326]](_images/math/0997425f7c76ba0b97a4f1ff91624127c26aa862.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
line 397
Mishra 7 objective function.
This class defines the Mishra 7 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra07}}(x) = \left [\prod_{i=1}^{n} x_i - n! \right]^2](_images/math/32aa970b56e1b650d56f0cb333ce2a1a30136bb8.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
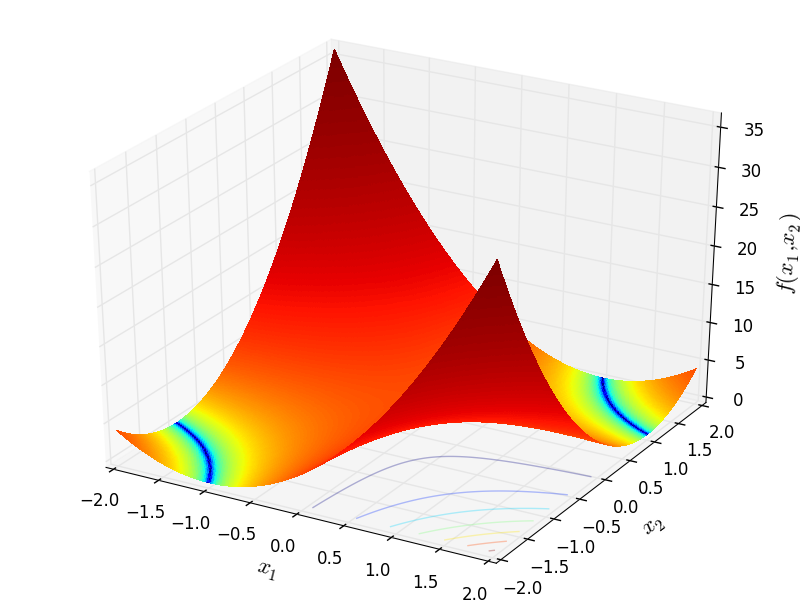
Two-dimensional Mishra07 function
Global optimum:  for
for 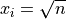 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Mishra 8 objective function.
This class defines the Mishra 8 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra08}}(x) = 0.001 \left[\lvert x_1^{10} - 20x_1^9
+ 180x_1^8 - 960 x_1^7 + 3360x_1^6 - 8064x_1^5 + 13340x_1^4 - 15360x_1^3
+ 11520x_1^2 - 5120x_1 + 2624 \rvert \lvert x_2^4 + 12x_2^3 + 54x_2^2
+ 108x_2 + 81 \rvert \right]^2](_images/math/910bd113e93496cadcf94fce94159870ad243ab8.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
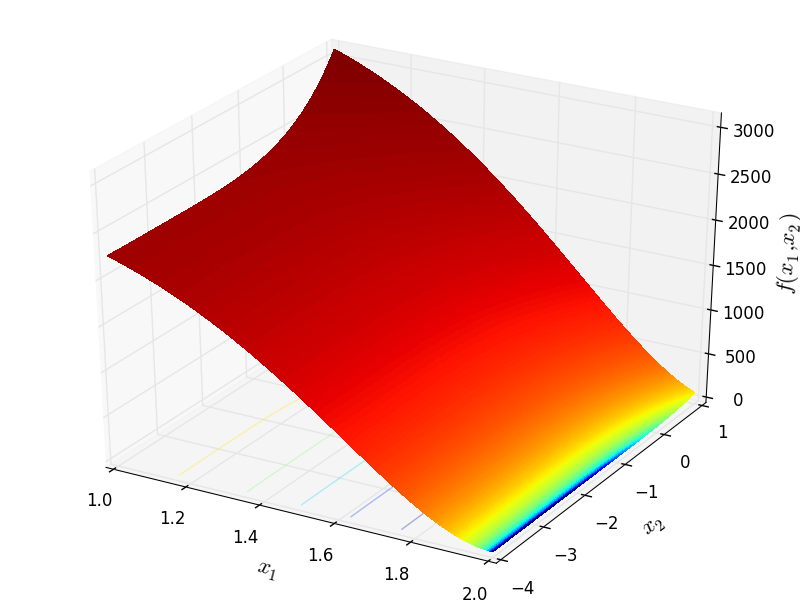
Two-dimensional Mishra08 function
Global optimum:  for
for ![x = [2, -3]](_images/math/2570e1e7f0a7fb488cffbaae74b24e543db426a7.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
Line 1065
Mishra 9 objective function.
This class defines the Mishra 9 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra09}}({x}) = \left[ ab^2c + abc^2 + b^2
+ (x_1 + x_2 - x_3)^2 \right]^2](_images/math/26a6a59d4eedf5bc0fb95d070c806aaa6be81b29.png)
Where, in this exercise:
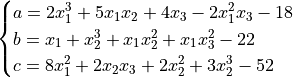
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 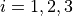 .
.
Global optimum:  for
for ![x = [1, 2, 3]](_images/math/717130b02b249ac3c5605d29a6ac31b6047d797e.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
Line 1103
Mishra 10 objective function.
This class defines the Mishra 10 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra10}}({x}) = \left[ \lfloor x_1 \perp x_2 \rfloor - \lfloor x_1 \rfloor - \lfloor x_2 \rfloor \right]^2](_images/math/408c856c677138ce95293379168331a61b2b9afc.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 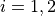 .
.
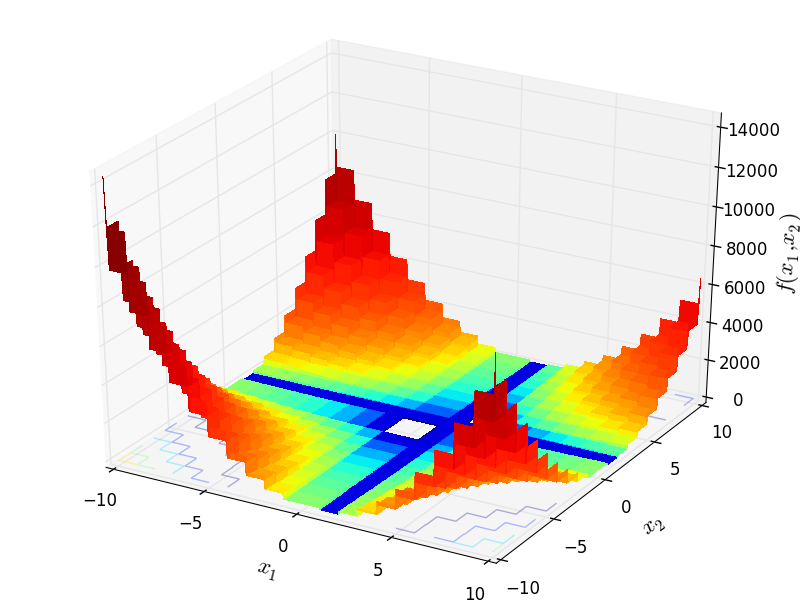
Two-dimensional Mishra10 function
Global optimum:  for
for ![x = [2, 2]](_images/math/22aaaba5ac24a1e2f3d8a44707560017185bd1dd.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
Mishra 10b objective function.
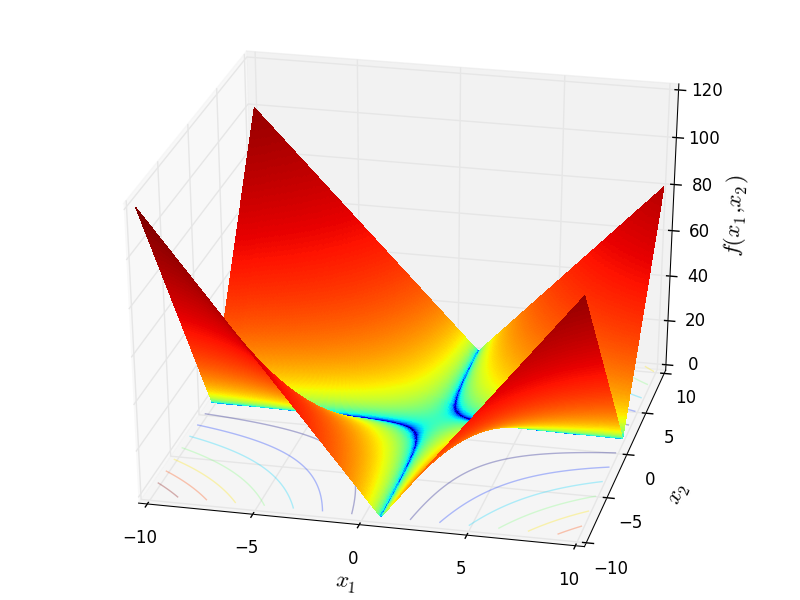
Two-dimensional Mishra10b function
Mishra 11 objective function.
This class defines the Mishra 11 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra11}}(x) = \left [ \frac{1}{n} \sum_{i=1}^{n} \lvert x_i
\rvert - \left(\prod_{i=1}^{n} \lvert x_i \rvert \right )^{\frac{1}{n}}
\right]^2](_images/math/92824e74c1768377f8a4c9b9fa6db73cce61c8c7.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
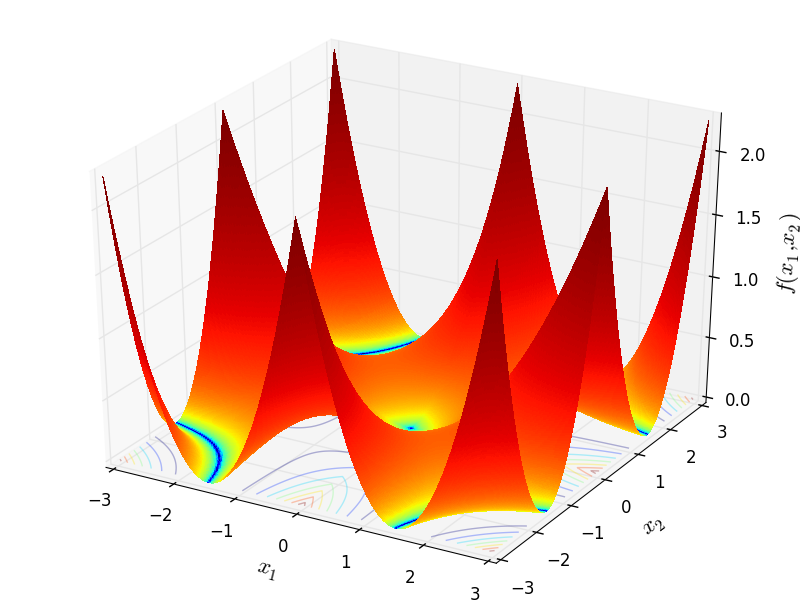
Two-dimensional Mishra11 function
Global optimum:  for
for 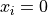 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
MullerBrown objective function.
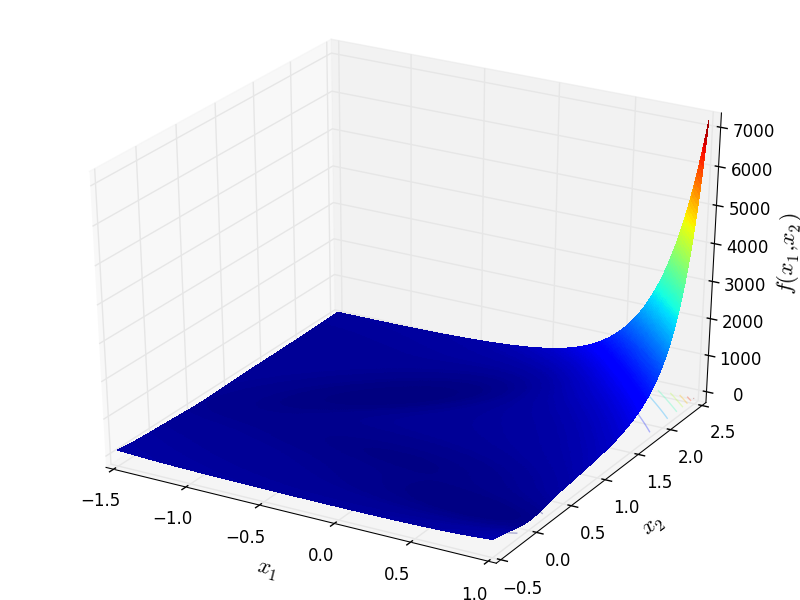
Two-dimensional MullerBrown function
MultiGaussian objective function.
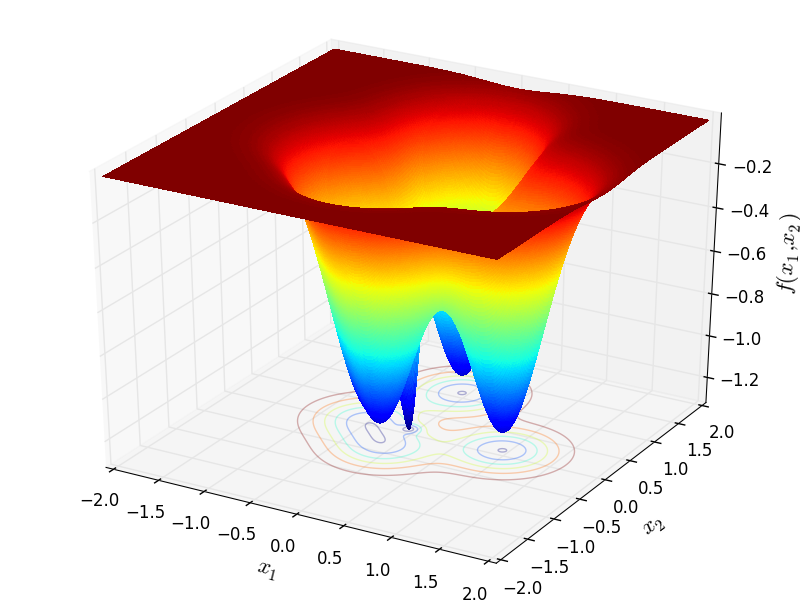
Two-dimensional MultiGaussian function
MultiModal objective function.
This class defines the MultiModal global optimization problem. This is a multimodal minimization problem defined as follows:
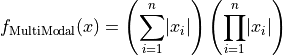
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
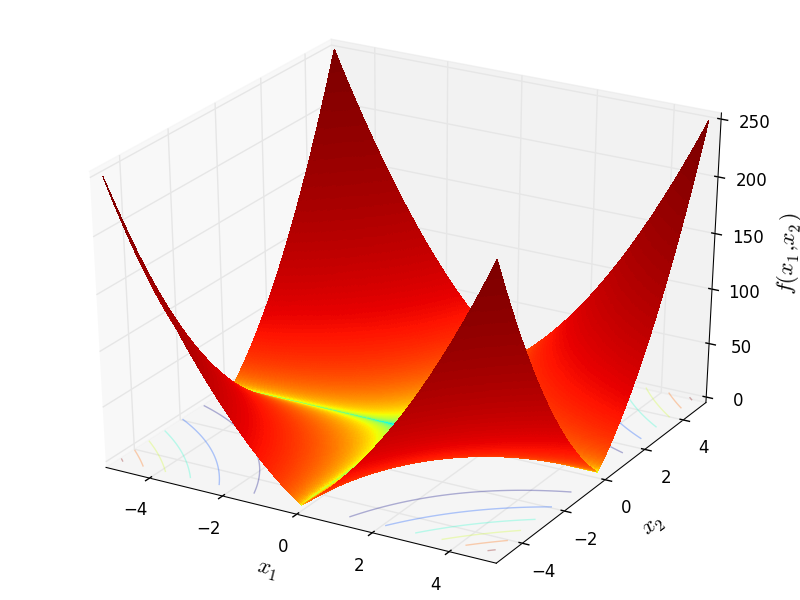
Two-dimensional MultiModal function
Global optimum:  for
for 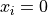 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO