Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions N
 N-D Test Functions N¶
N-D Test Functions N¶NeedleEye objective function.
This class defines the Needle-Eye global optimization problem. This is a a multimodal minimization problem defined as follows:
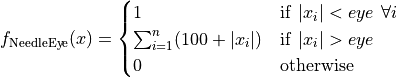
Where, in this exercise, 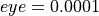 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
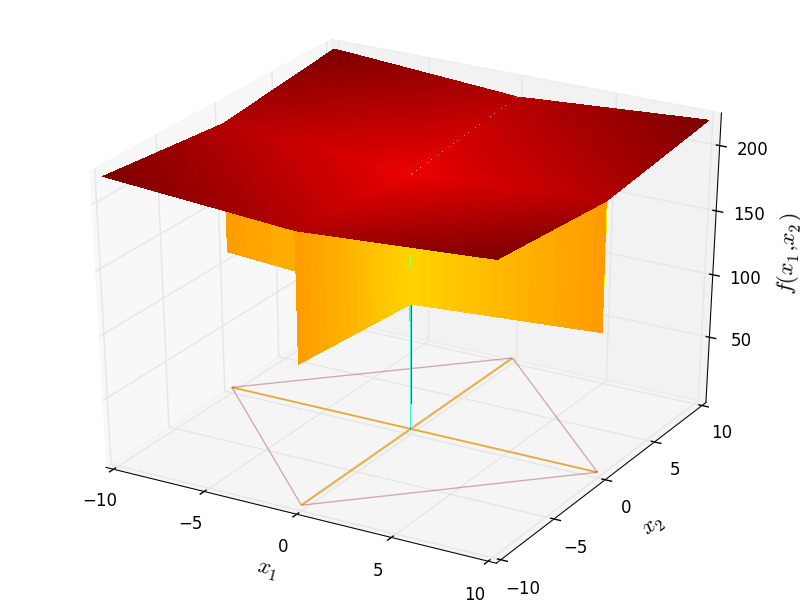
Two-dimensional NeedleEye function
Global optimum: 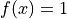 for
for 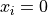 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
NewFunction01 objective function.
This class defines the NewFunction01 global optimization problem. This is a multimodal minimization problem defined as follows:
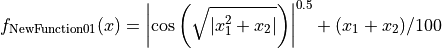
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
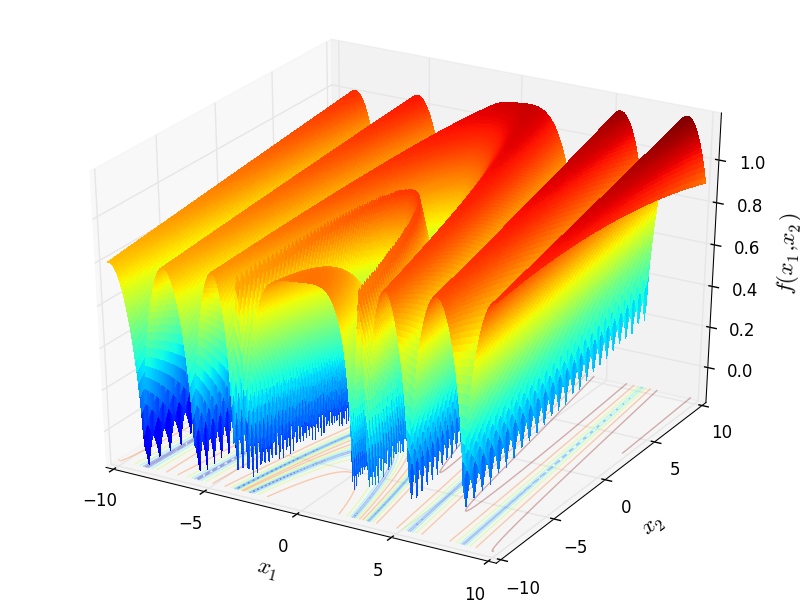
Two-dimensional NewFunction01 function
Global optimum: 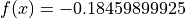 for
for
![x = [-8.46669057, -9.99982177]](_images/math/a403f54062b9d78f1d9e2be85516604fd09fd10e.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
NewFunction02 objective function.
This class defines the NewFunction02 global optimization problem. This is a multimodal minimization problem defined as follows:
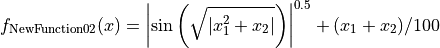
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
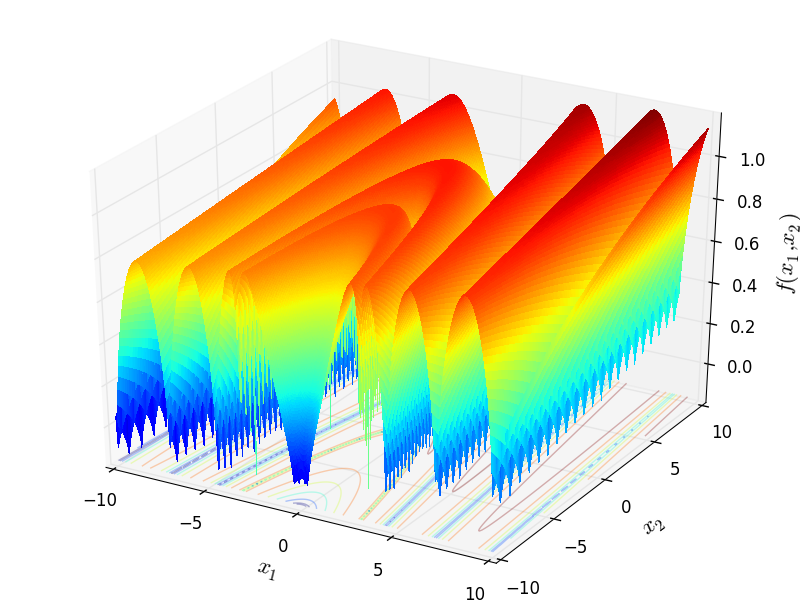
Two-dimensional NewFunction02 function
Global optimum: 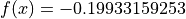 for
for
![x = [-9.94103375, -9.99771235]](_images/math/7ef4cbc9eee6b4d2854e6a049931c504a094c2b0.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Warning
minimum value is estimated from running many optimisations and choosing the best.