Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions T
 N-D Test Functions T¶
N-D Test Functions T¶TestTubeHolder objective function.
This class defines the TestTubeHolder global optimization problem. This is a multimodal minimization problem defined as follows:
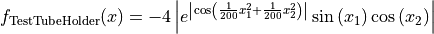
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
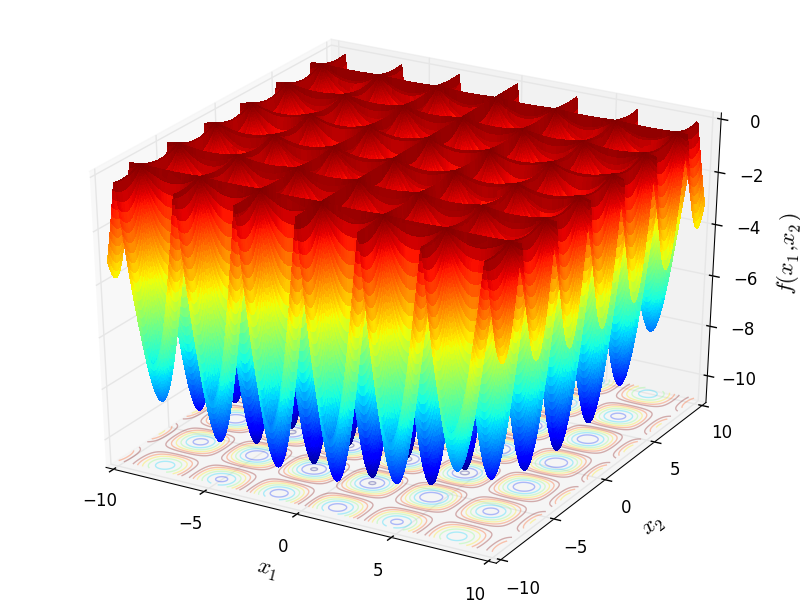
Two-dimensional TestTubeHolder function
Global optimum: 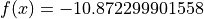 for
for
![x= [-\pi/2, 0]](_images/math/1029f5581252c79984da1db6992af52860d280b2.png)
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Three Hump Camel objective function.
This class defines the Three Hump Camel global optimization problem. This is a multimodal minimization problem defined as follows:
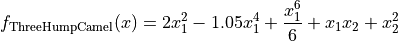
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
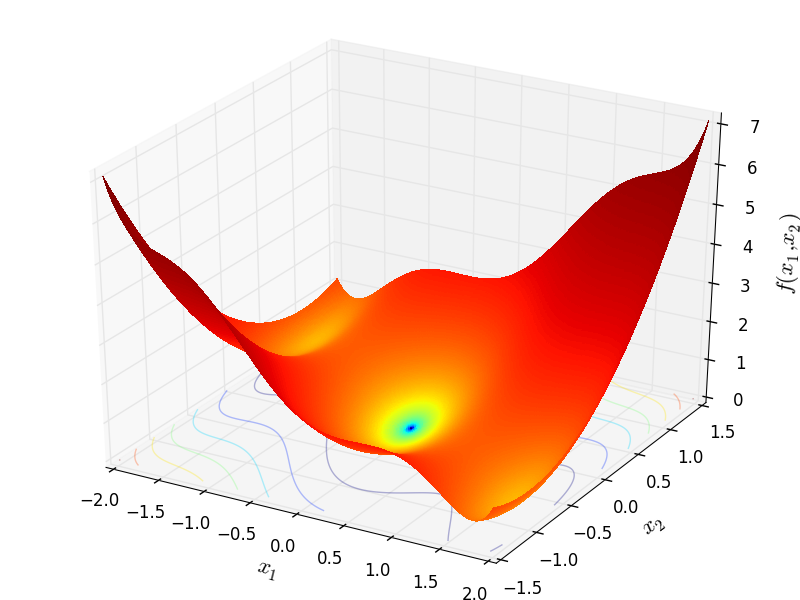
Two-dimensional ThreeHumpCamel function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Thurber objective function.
Treccani objective function.
This class defines the Treccani global optimization problem. This is a multimodal minimization problem defined as follows:
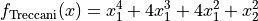
with ![x_i \in
[-5, 5]](_images/math/367345cb1acab0e08fd68cc48327c4d9bd482db4.png) for
for  .
.
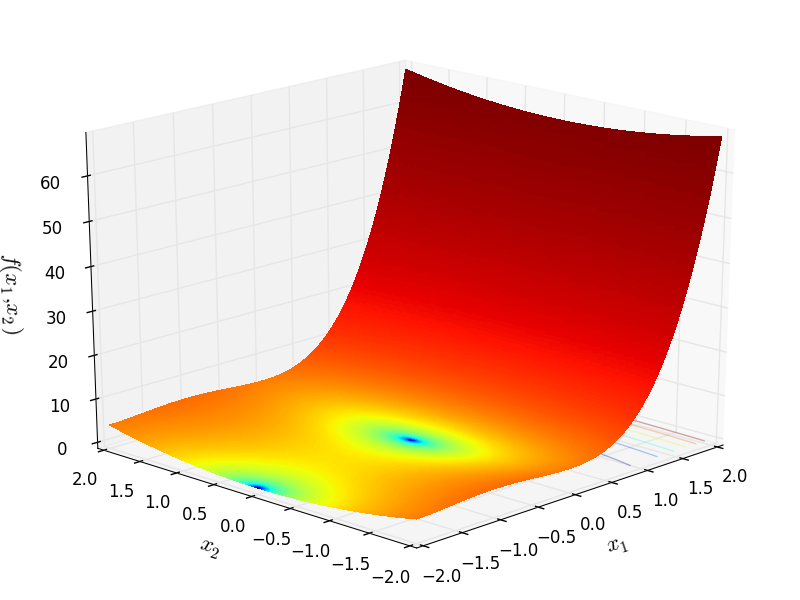
Two-dimensional Treccani function
Global optimum:  for
for ![x = [-2, 0]](_images/math/321a928bb7d0575612ee4d7eb9b253e073236e9b.png) or
or
![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Trefethen objective function.
This class defines the Trefethen global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trefethen}}(x) = 0.25 x_{1}^{2} + 0.25 x_{2}^{2}
+ e^{\sin\left(50 x_{1}\right)}
- \sin\left(10 x_{1} + 10 x_{2}\right)
+ \sin\left(60 e^{x_{2}}\right)
+ \sin\left[70 \sin\left(x_{1}\right)\right]
+ \sin\left[\sin\left(80 x_{2}\right)\right]](_images/math/56713dc81539262c1205aa915499a236a892e81d.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
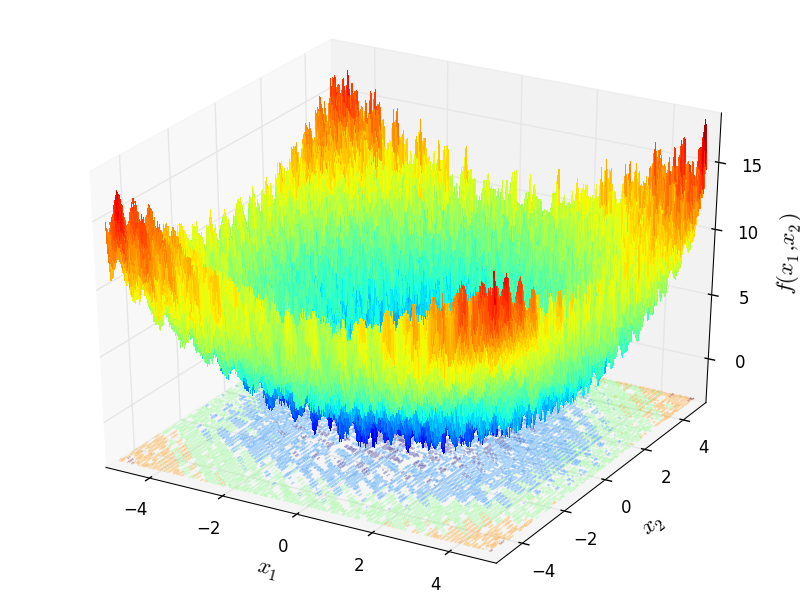
Two-dimensional Trefethen function
Global optimum: 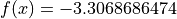 for
for
![x = [-0.02440307923, 0.2106124261]](_images/math/6f13b326bf2b4104c04c493268f861a6985921ed.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Trid objective function.
This class defines the Trid global optimization problem. This is a multimodal minimization problem defined as follows:
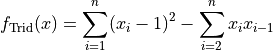
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-20, 20]](_images/math/026a917a812dbaef4e7a8ea87e9963bb111e2644.png) for
for 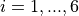 .
.
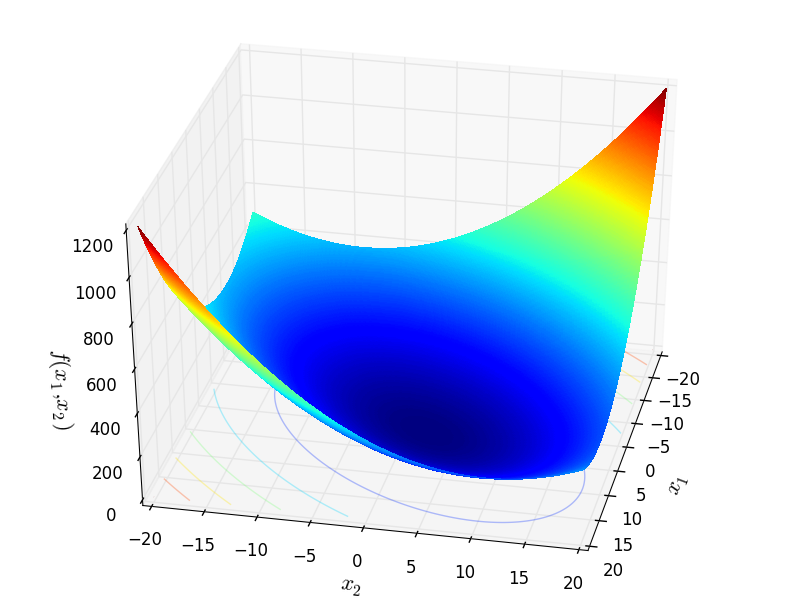
Two-dimensional Trid function
Global optimum: 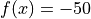 for
for ![x = [6, 10, 12, 12, 10, 6]](_images/math/317223c592573b35696bf175ec7cba26d6953cf9.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil#150, starting index of second summation term should be 2.
TridiagonalMatrix objective function.
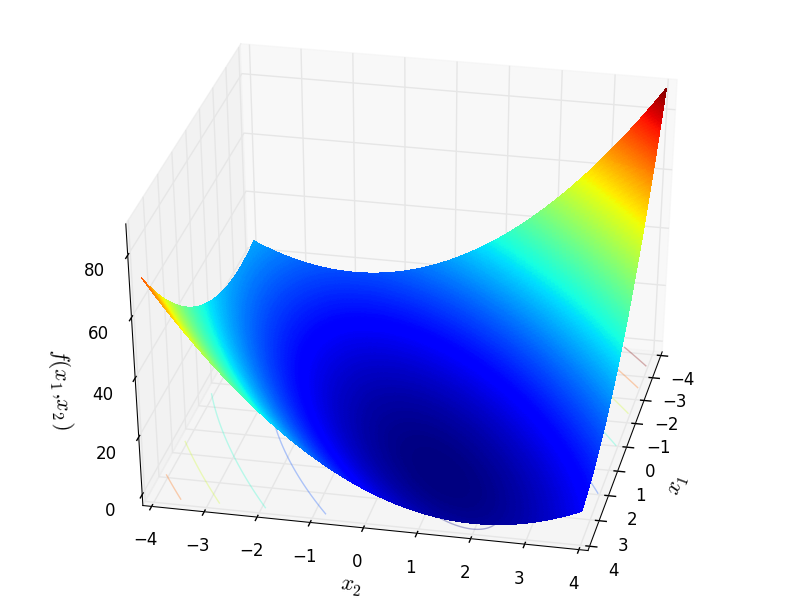
Two-dimensional TridiagonalMatrix function
Trigonometric 1 objective function.
This class defines the Trigonometric 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trigonometric01}}(x) = \sum_{i=1}^{n} \left [n -
\sum_{j=1}^{n} \cos(x_j)
+ i \left(1 - cos(x_i)
- sin(x_i) \right ) \right]^2](_images/math/74a4220ee0df88da63c4c9ac9fb8095551719b6f.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, \pi]](_images/math/10b9f829ecf73e20ecc5c80159a1d1615d4c0f6a.png) for
for  .
.
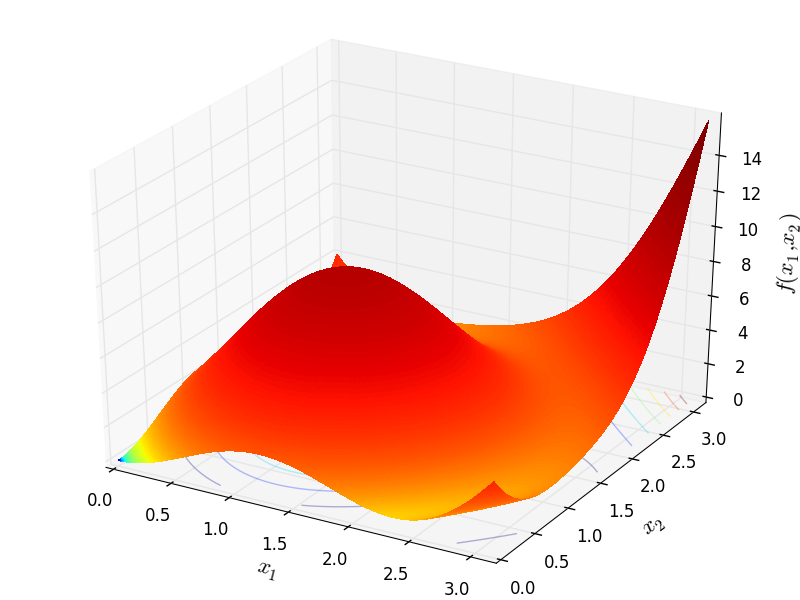
Two-dimensional Trigonometric01 function
Global optimum:  for
for 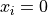 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
equaiton uncertain here. Is it just supposed to be the cos term in the inner sum, or the whole of the second line in Jamil #153.
Trigonometric 2 objective function.
This class defines the Trigonometric 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trigonometric2}}(x) = 1 + \sum_{i=1}^{n} 8 \sin^2
\left[7(x_i - 0.9)^2 \right]
+ 6 \sin^2 \left[14(x_i - 0.9)^2 \right]
+ (x_i - 0.9)^2](_images/math/46a27cad9b5224f2a793654917d48366c2f54638.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
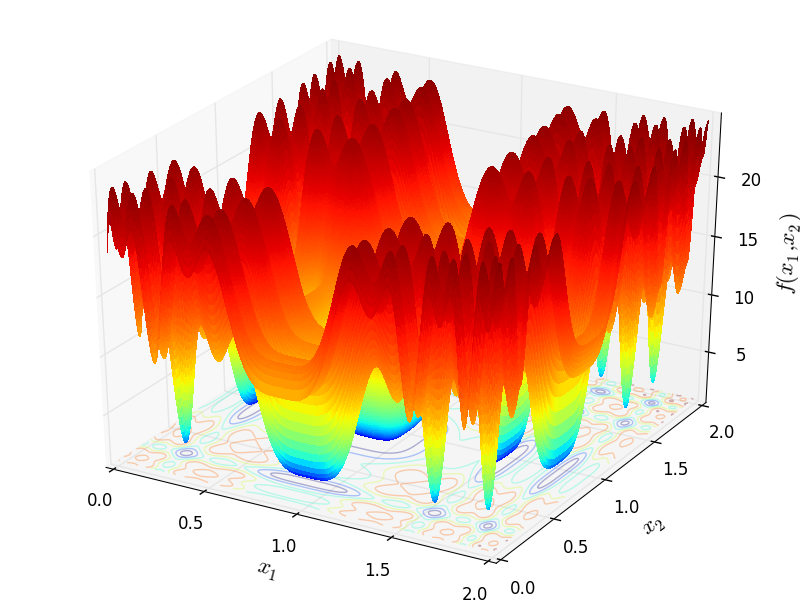
Two-dimensional Trigonometric02 function
Global optimum: 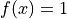 for
for  for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Tripod objective function.
This class defines the Tripod global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Tripod}}(x) = p(x_2) \left[1 + p(x_1) \right] +
\lvert x_1 + 50p(x_2) \left[1 - 2p(x_1) \right]
\rvert + \lvert x_2 + 50\left[1 - 2p(x_2)\right]
\rvert](_images/math/857c69e4463ca47c6695b594a31bddec1eaa88e3.png)
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
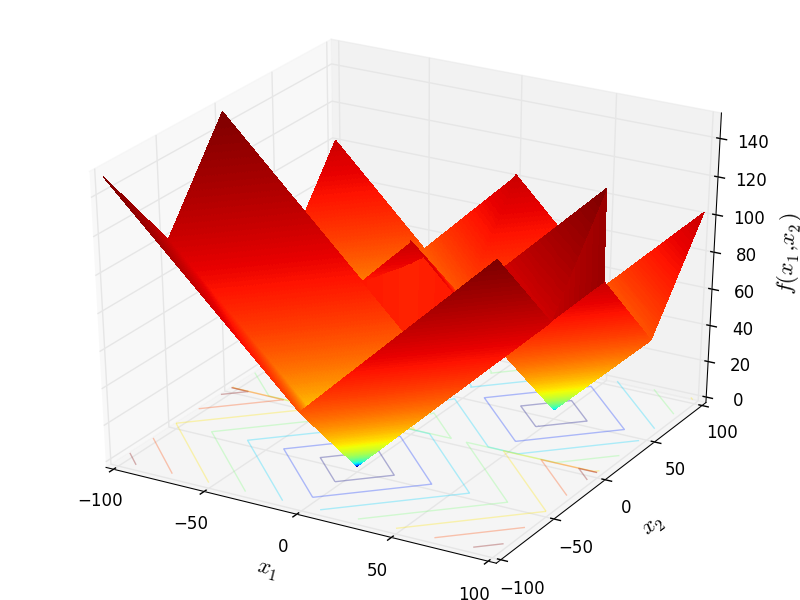
Two-dimensional Tripod function
Global optimum:  for
for ![x = [0, -50]](_images/math/e62fcd4cf1f721fde28f3d99ab6c5081a6567108.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Tsoulos objective function.
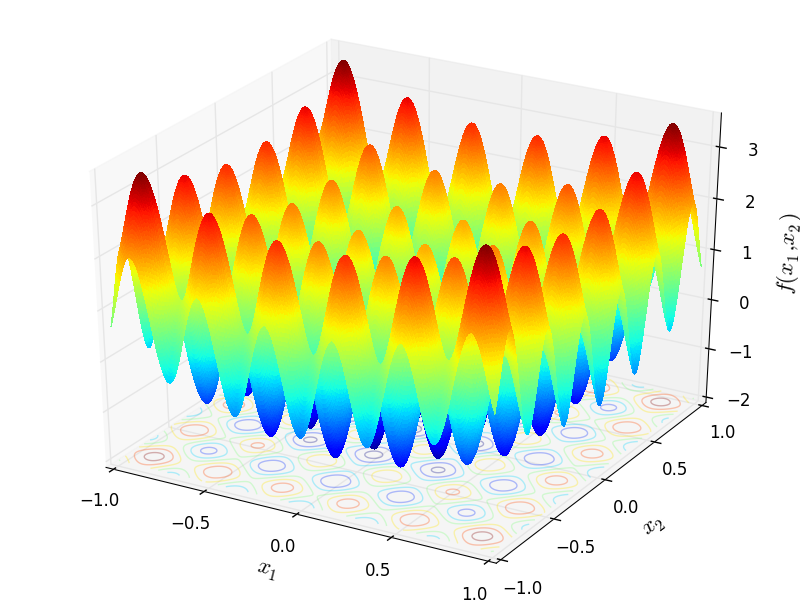
Two-dimensional Tsoulos function