Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions S
 N-D Test Functions S¶
N-D Test Functions S¶Salomon objective function.
This class defines the Salomon global optimization problem. This is a multimodal minimization problem defined as follows:
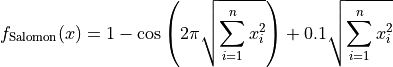
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-100, 100]](_images/math/d8fb57bba3ab0918fa5f82c87dbf208e957d26dc.png) for
for  .
.
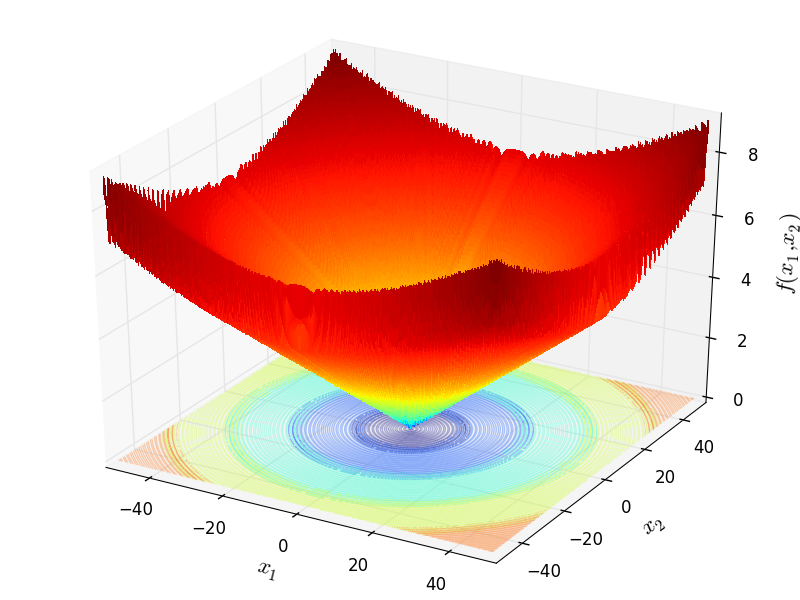
Two-dimensional Salomon function
Global optimum:  for
for 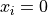 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Sargan objective function.
This class defines the Sargan global optimization problem. This is a multimodal minimization problem defined as follows:
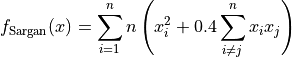
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for
 .
.
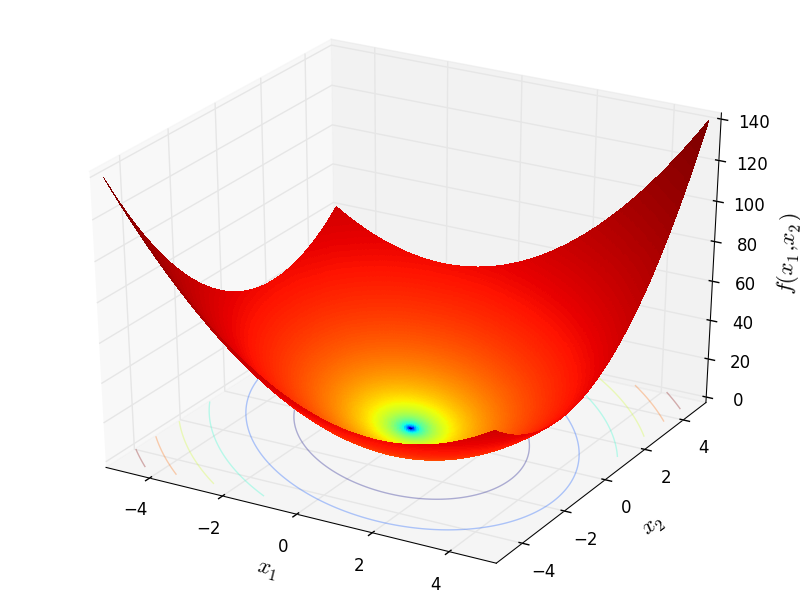
Two-dimensional Sargan function
Global optimum:  for
for 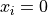 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
SawtoothXY objective function.
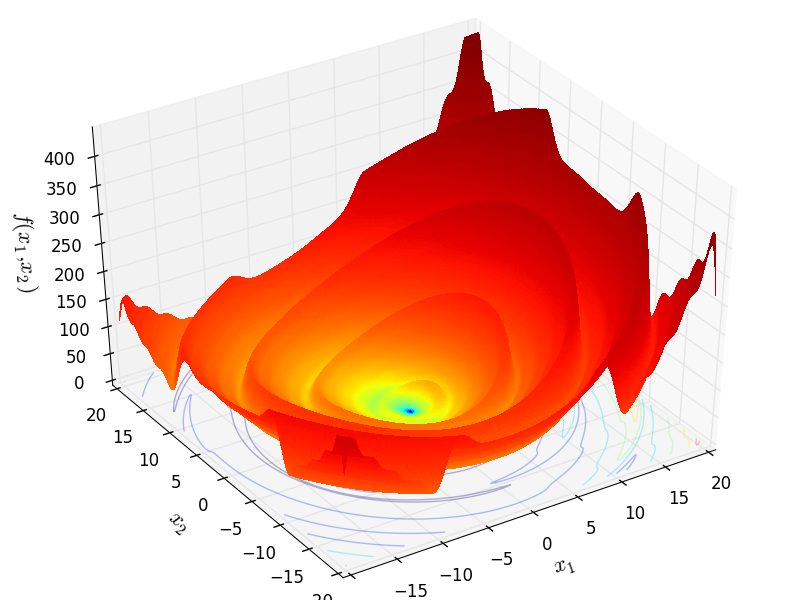
Two-dimensional SawtoothXY function
Schaffer 1 objective function.
This class defines the Schaffer 1 global optimization problem. This is a multimodal minimization problem defined as follows:
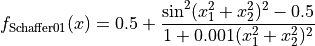
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
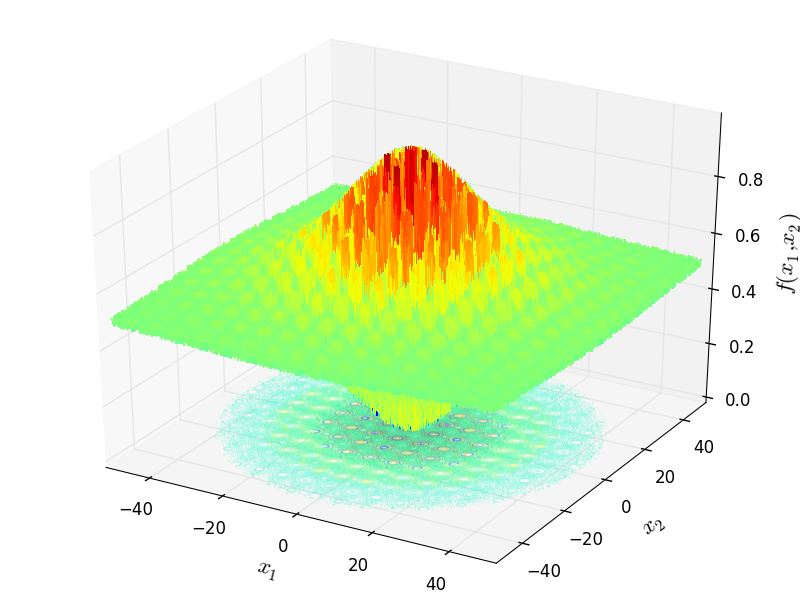
Two-dimensional Schaffer01 function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png) for
for

Mishra, S. Some new test functions for global optimization and performance of repulsive particle swarm method. Munich Personal RePEc Archive, 2006, 2718
Schaffer 2 objective function.
This class defines the Schaffer 2 global optimization problem. This is a multimodal minimization problem defined as follows:
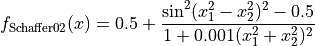
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
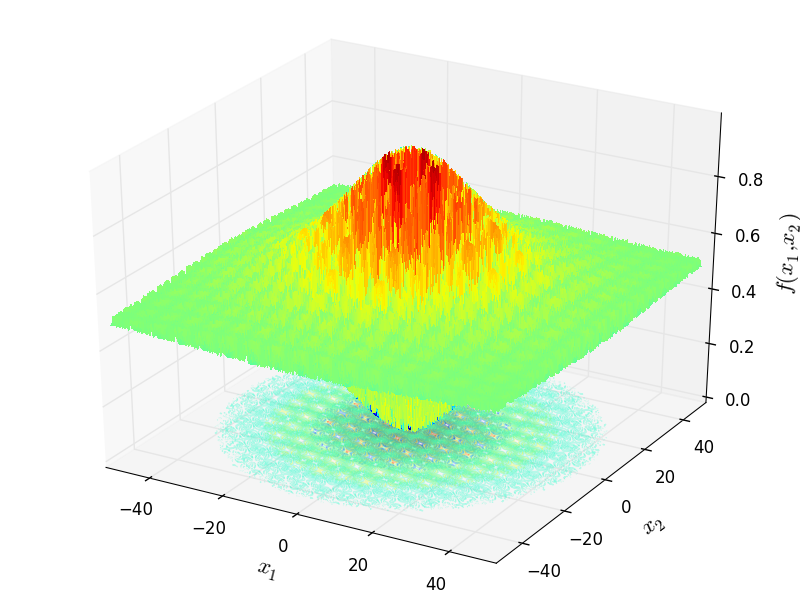
Two-dimensional Schaffer02 function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png) for
for

Mishra, S. Some new test functions for global optimization and performance of repulsive particle swarm method. Munich Personal RePEc Archive, 2006, 2718
Schaffer 3 objective function.
This class defines the Schaffer 3 global optimization problem. This is a multimodal minimization problem defined as follows:
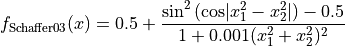
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
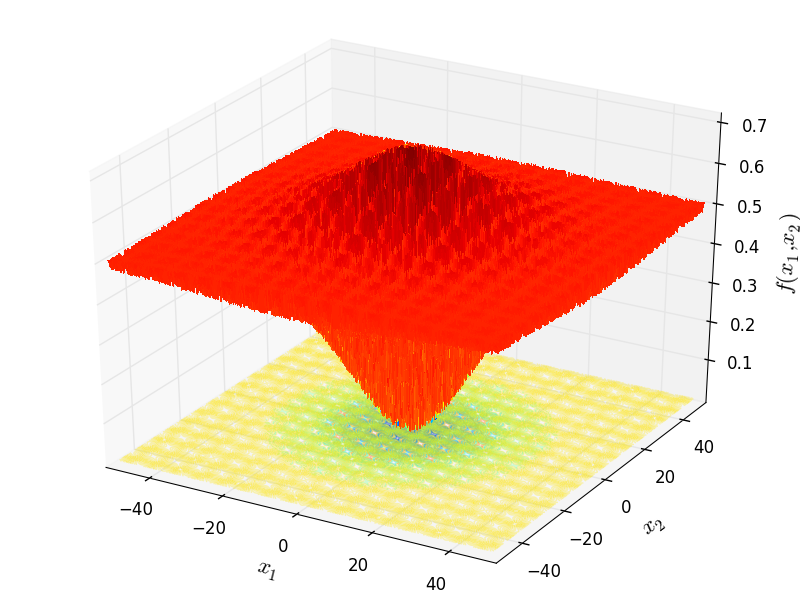
Two-dimensional Schaffer03 function
Global optimum: 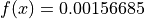 for
for ![x = [0, 1.253115]](_images/math/f56b78865897376f6a9605acad3cf243e0584de7.png)
Mishra, S. Some new test functions for global optimization and performance of repulsive particle swarm method. Munich Personal RePEc Archive, 2006, 2718
Schaffer 4 objective function.
This class defines the Schaffer 4 global optimization problem. This is a multimodal minimization problem defined as follows:
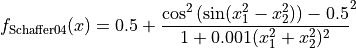
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
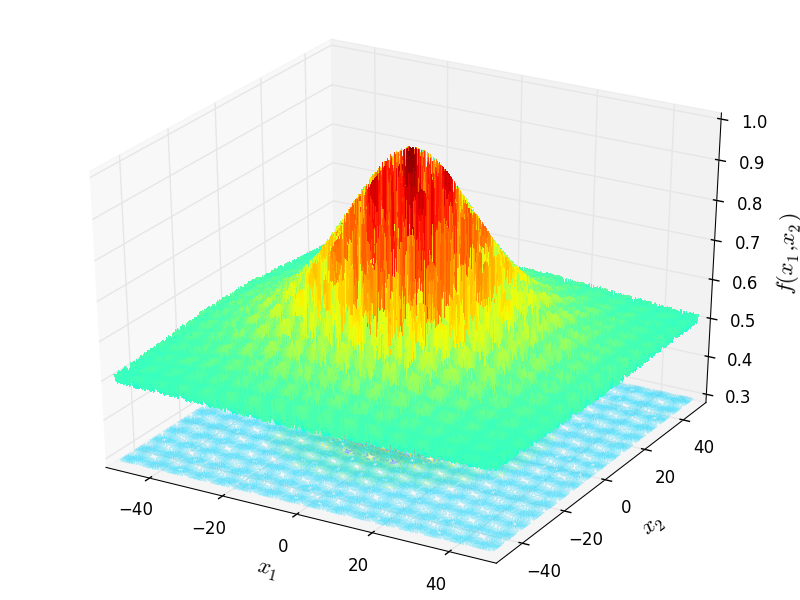
Two-dimensional Schaffer04 function
Global optimum: 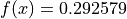 for
for ![x = [0, 1.253115]](_images/math/f56b78865897376f6a9605acad3cf243e0584de7.png)
Mishra, S. Some new test functions for global optimization and performance of repulsive particle swarm method. Munich Personal RePEc Archive, 2006, 2718
Schmidt-Vetters objective function.
This class defines the Schmidt-Vetters global optimization problem. This is a multimodal minimization problem defined as follows:
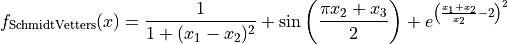
with ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for 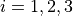 .
.
Global optimum: 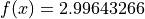 for
for
![x = [0.79876108, 0.79962581, 0.79848824]](_images/math/257d4ca82fd1500f3b9554be3d2530ce1fa84763.png)
Todo
equation seems right, but [7.07083412 , 10., 3.14159293] produces a lower minimum, 0.193973
Schwefel 1 objective function.
This class defines the Schwefel 1 global optimization problem. This is a unimodal minimization problem defined as follows:
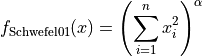
Where, in this exercise, 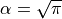 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
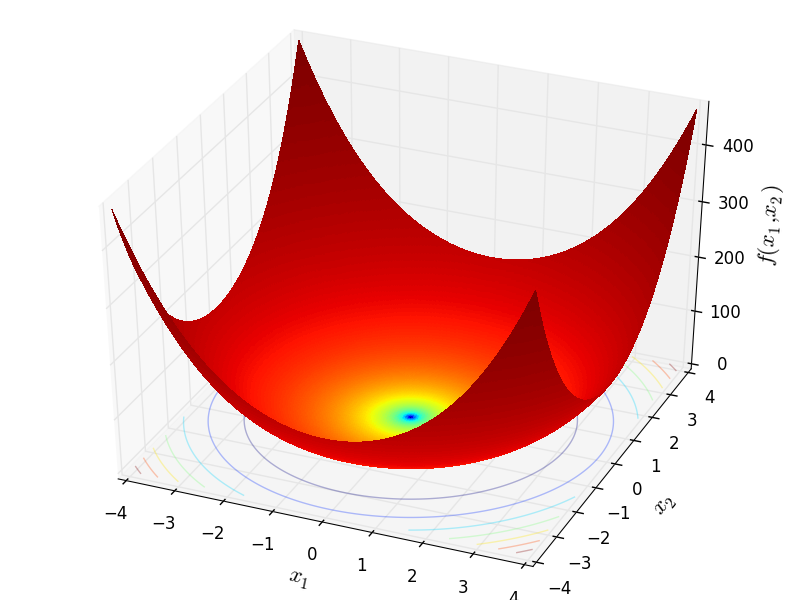
Two-dimensional Schwefel01 function
Global optimum:  for
for 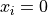 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 2 objective function.
This class defines the Schwefel 2 global optimization problem. This is a unimodal minimization problem defined as follows:
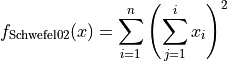
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
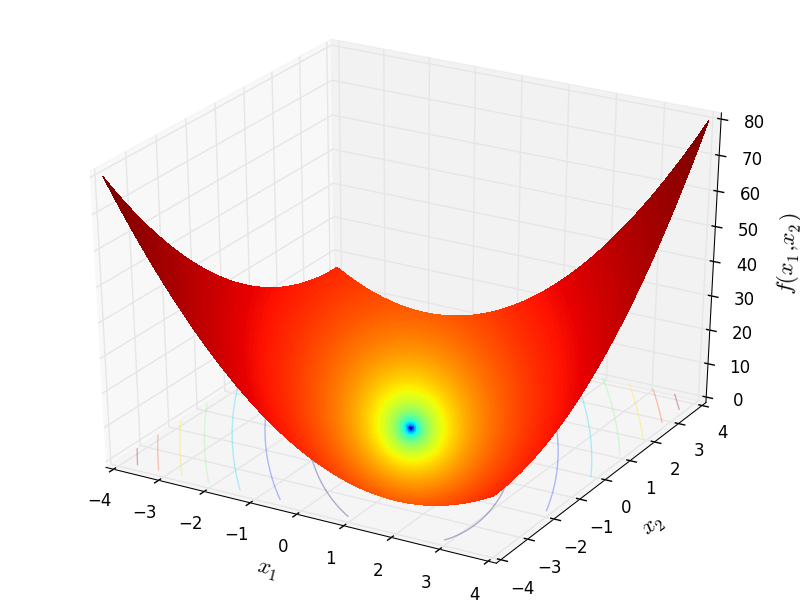
Two-dimensional Schwefel02 function
Global optimum:  for
for 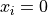 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 4 objective function.
This class defines the Schwefel 4 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Schwefel04}}(x) = \sum_{i=1}^n \left[(x_i - 1)^2
+ (x_1 - x_i^2)^2 \right]](_images/math/4f75e1079b772439edbb3f496bcaed4639357f6a.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
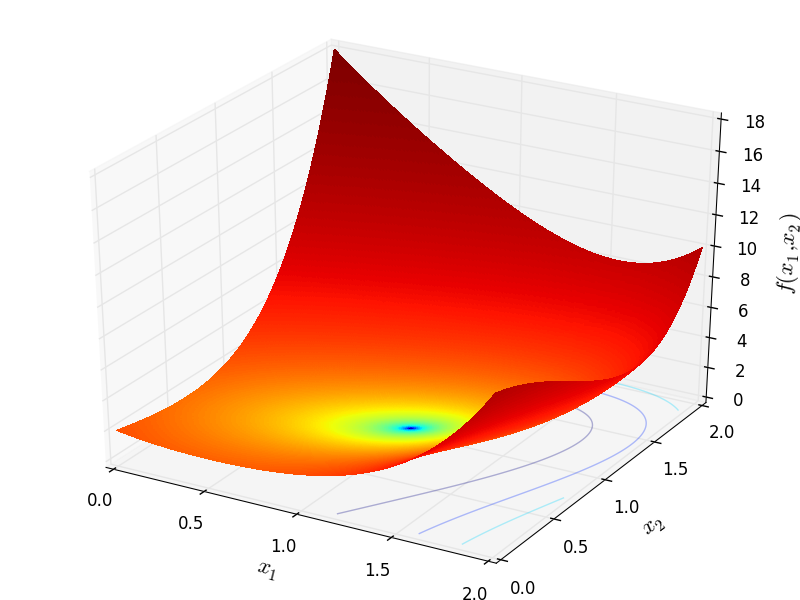
Two-dimensional Schwefel04 function
Global optimum:  for:math:x_i = 1 for
for:math:x_i = 1 for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 6 objective function.
This class defines the Schwefel 6 global optimization problem. This is a unimodal minimization problem defined as follows:
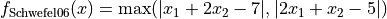
with ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
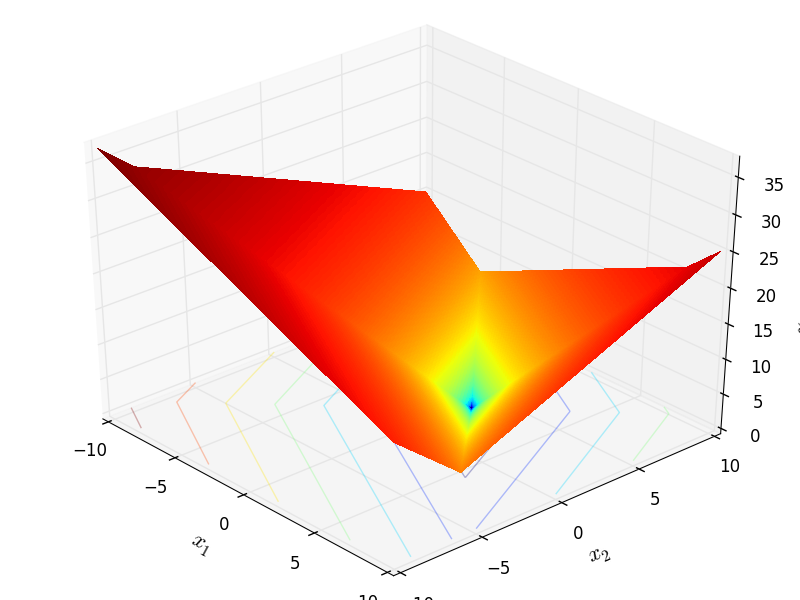
Two-dimensional Schwefel06 function
Global optimum:  for
for ![x = [1, 3]](_images/math/4523ef74846622a8d2b61339f3c111ea5fdb745f.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 20 objective function.
This class defines the Schwefel 20 global optimization problem. This is a unimodal minimization problem defined as follows:
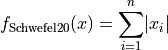
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
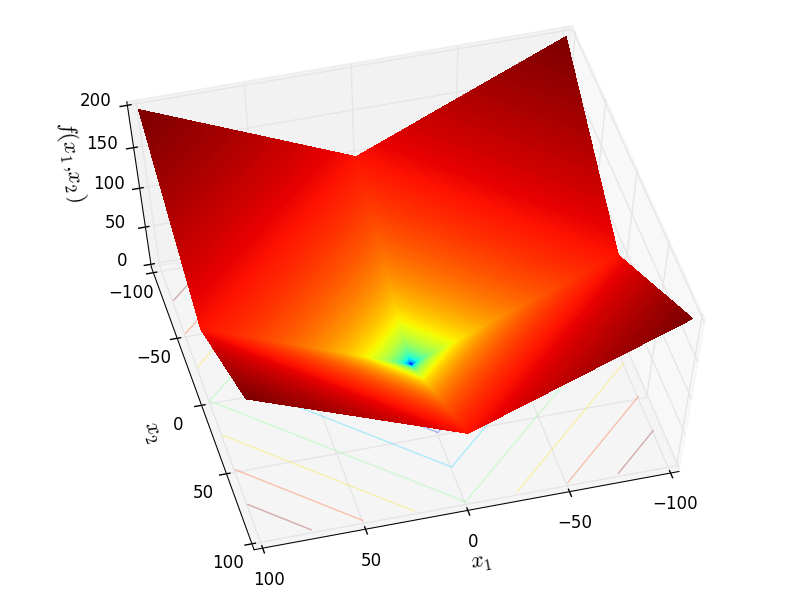
Two-dimensional Schwefel20 function
Global optimum:  for
for 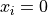 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil #122 is incorrect. There shouldn’t be a leading minus sign.
Schwefel 21 objective function.
This class defines the Schwefel 21 global optimization problem. This is a unimodal minimization problem defined as follows:
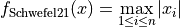
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
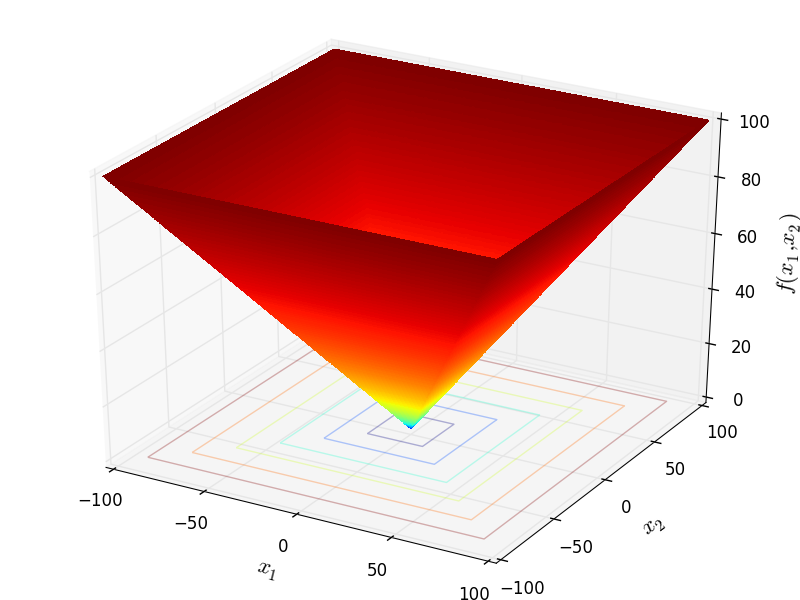
Two-dimensional Schwefel21 function
Global optimum:  for
for 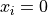 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 22 objective function.
This class defines the Schwefel 22 global optimization problem. This is a multimodal minimization problem defined as follows:
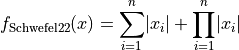
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.

Two-dimensional Schwefel22 function
Global optimum:  for
for 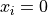 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Schwefel 26 objective function.
This class defines the Schwefel 26 global optimization problem. This is a multimodal minimization problem defined as follows:
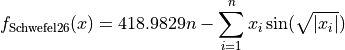
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
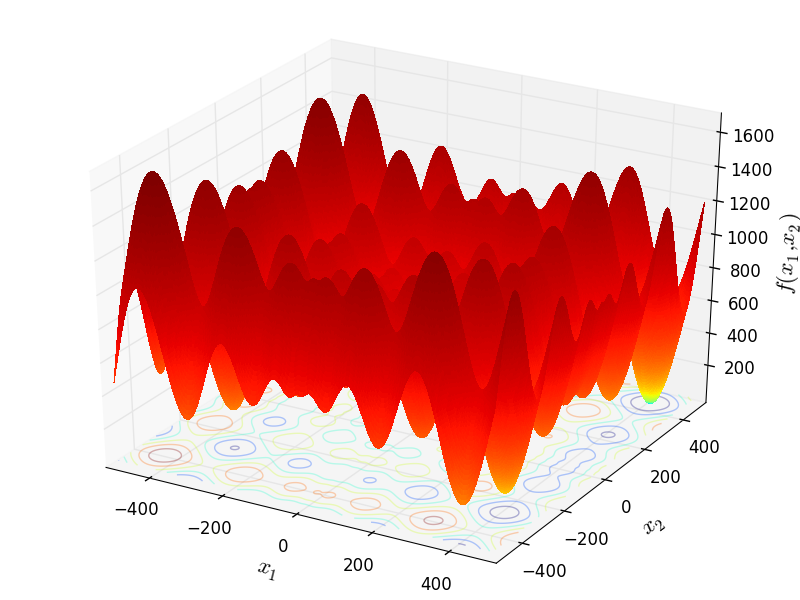
Two-dimensional Schwefel26 function
Global optimum:  for
for 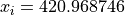 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Schwefel 36 objective function.
This class defines the Schwefel 36 global optimization problem. This is a multimodal minimization problem defined as follows:
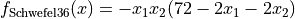
with ![x_i \in [0, 500]](_images/math/da5613ad206e6bb117f3e6258874921cda1ab408.png) for
for  .
.
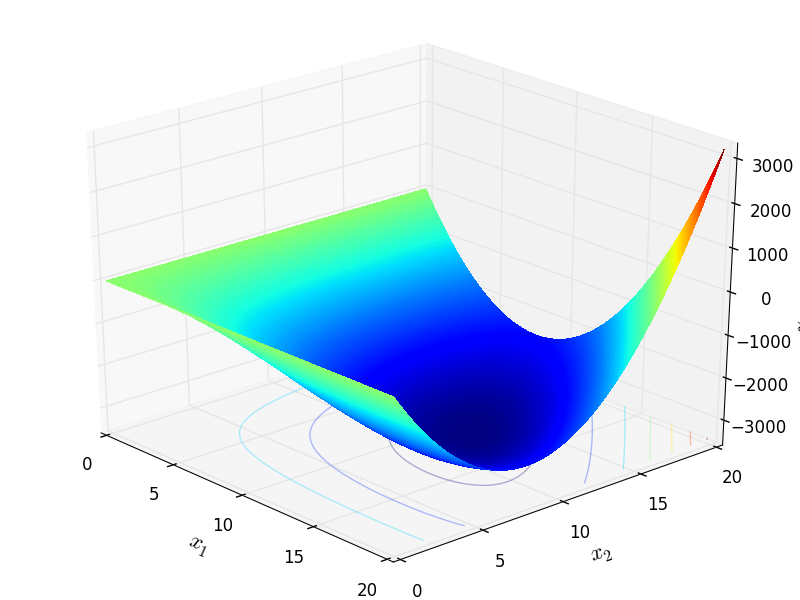
Two-dimensional Schwefel36 function
Global optimum: 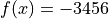 for
for ![x = [12, 12]](_images/math/3090f8fe0e255c7fc6b3b3b2a37cc933a40cf94c.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Shekel 5 objective function.
This class defines the Shekel 5 global optimization problem. This is a multimodal minimization problem defined as follows:
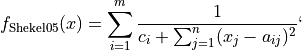
Where, in this exercise:

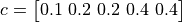
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for 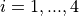 .
.
Global optimum: 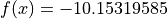 for
for 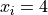 for
for
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
this is a different global minimum compared to Jamil#130. The minimum is found by doing lots of optimisations. The solution is supposed to be at [4] * N, is there any numerical overflow?
Shekel 7 objective function.
This class defines the Shekel 7 global optimization problem. This is a multimodal minimization problem defined as follows:
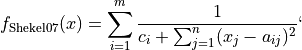
Where, in this exercise:

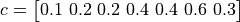
with ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for 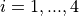 .
.
Global optimum: 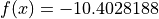 for
for 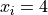 for
for
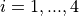
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
this is a different global minimum compared to Jamil#131. This minimum is obtained after running lots of minimisations! Is there any numerical overflow that causes the minimum solution to not be [4] * N?
Shekel 10 objective function.
This class defines the Shekel 10 global optimization problem. This is a multimodal minimization problem defined as follows:
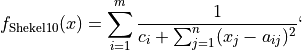
Where, in this exercise:

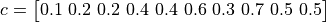
with ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for 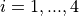 .
.
Global optimum: 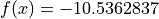 for
for 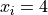 for
for
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Found a lower global minimum than Jamil#132... Is this numerical overflow?
Shubert 1 objective function.
This class defines the Shubert 1 global optimization problem. This is a multimodal minimization problem defined as follows:
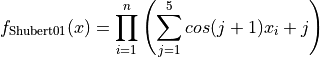
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
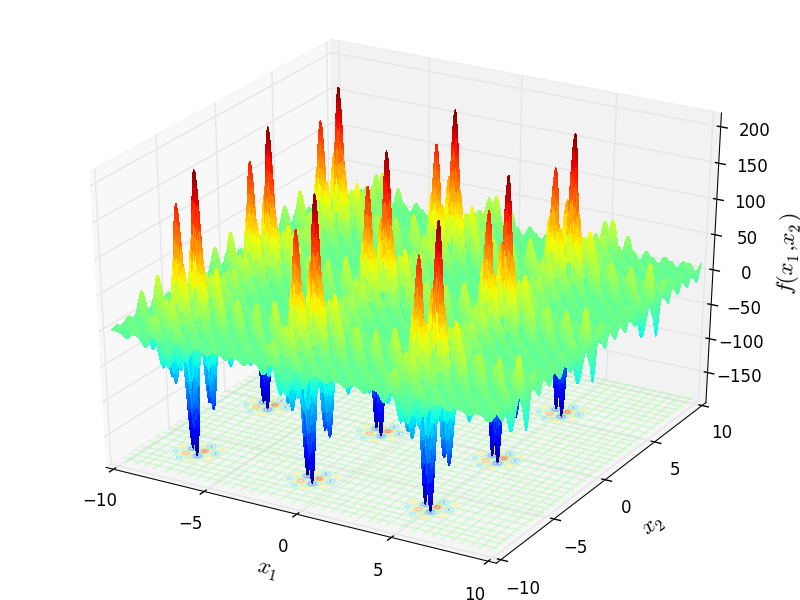
Two-dimensional Shubert01 function
Global optimum:  for
for
![x = [-7.0835, 4.8580]](_images/math/079bf849ad039d0f1b90ec197403b05f59da9fe0.png) (and many others).
(and many others).
Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil#133 is missing a prefactor of j before the cos function.
Shubert 3 objective function.
This class defines the Shubert 3 global optimization problem. This is a multimodal minimization problem defined as follows:
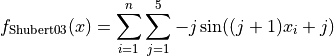
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
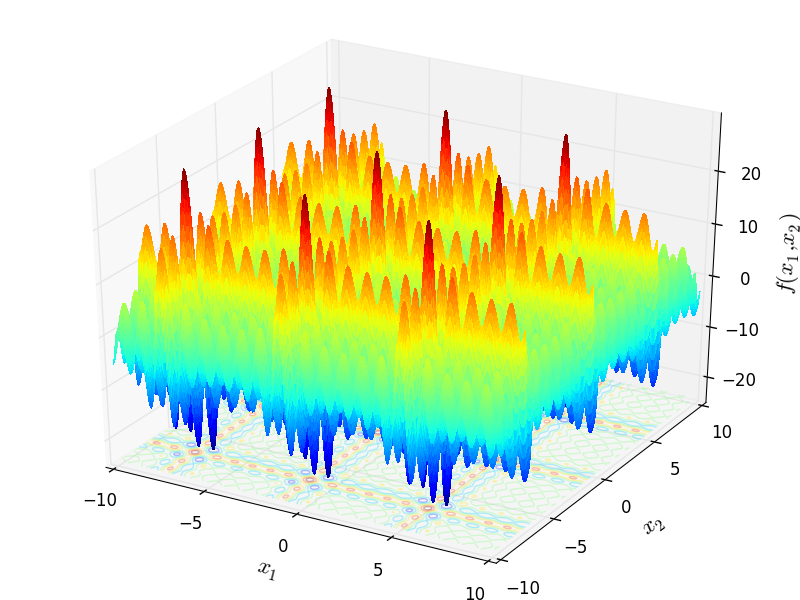
Two-dimensional Shubert03 function
Global optimum: 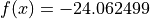 for
for
![x = [5.791794, 5.791794]](_images/math/2883b183795fcd0302bbcaf1b6eaaaabe7f78836.png) (and many others).
(and many others).
Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil#134 has wrong global minimum value, and is missing a minus sign before the whole thing.
Shubert 4 objective function.
This class defines the Shubert 4 global optimization problem. This is a multimodal minimization problem defined as follows:
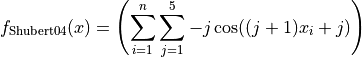
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
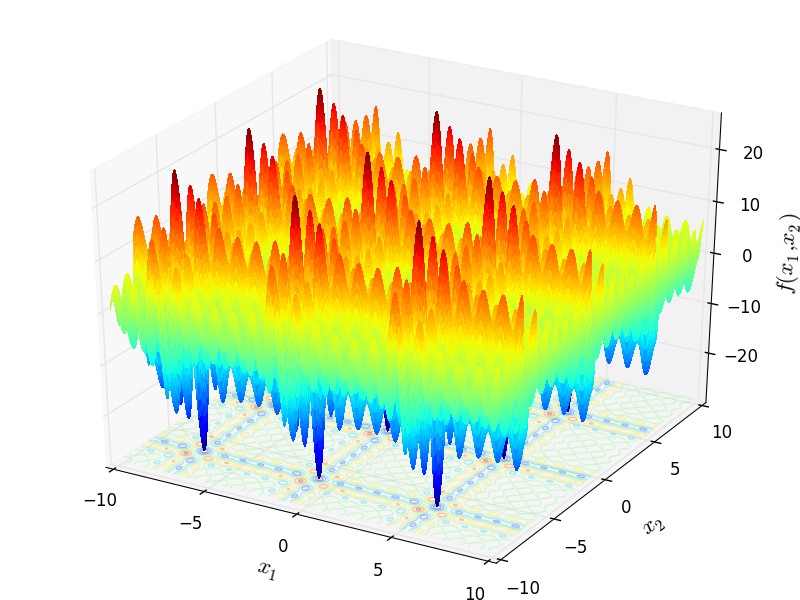
Two-dimensional Shubert04 function
Global optimum: 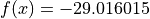 for
for
![x = [-0.80032121, -7.08350592]](_images/math/9e0b5af6ae70ddca1d1b6d2efe2f49a82de4e4d2.png) (and many others).
(and many others).
Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil#135 has wrong global minimum value, and is missing a minus sign before the whole thing.
Simpleton objective function.
SineEnvelope objective function.
This class defines the SineEnvelope global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{SineEnvelope}}(x) = -\sum_{i=1}^{n-1}\left[\frac{\sin^2(
\sqrt{x_{i+1}^2+x_{i}^2}-0.5)}
{(0.001(x_{i+1}^2+x_{i}^2)+1)^2}
+ 0.5\right]](_images/math/c8b61f5918fcbd93e812d1cc965e53b5412a0dd3.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
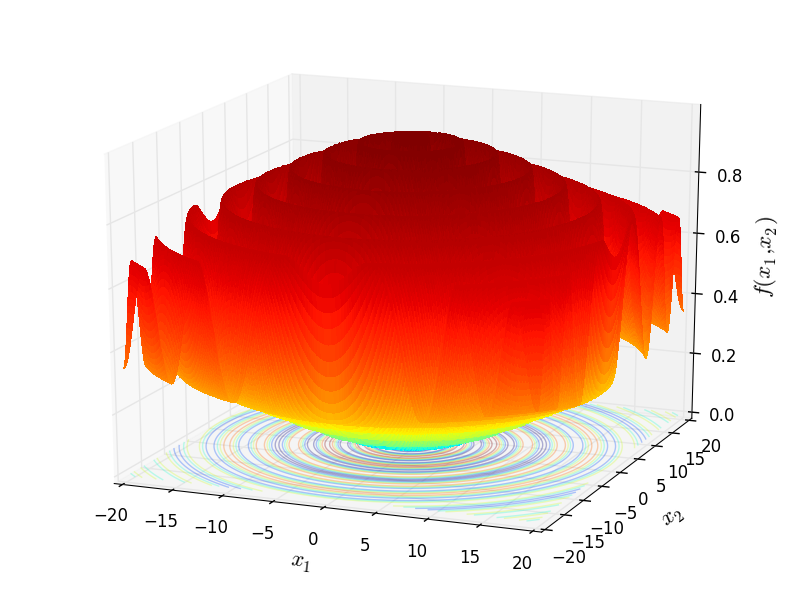
Two-dimensional SineEnvelope function
Global optimum:  for
for 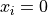 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil #136
Sinusoidal objective function.
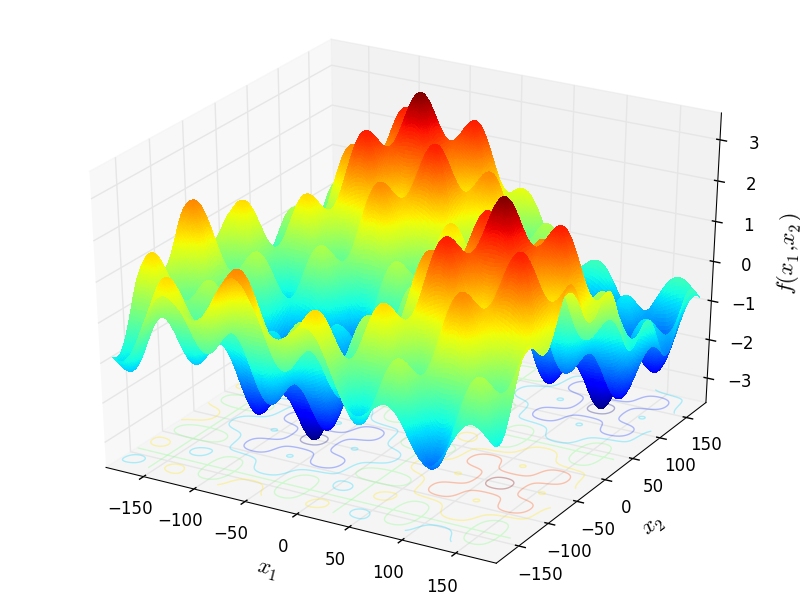
Two-dimensional Sinusoidal function
Six Hump Camel objective function.
This class defines the Six Hump Camel global optimization problem. This is a multimodal minimization problem defined as follows:
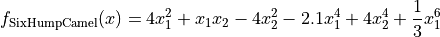
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
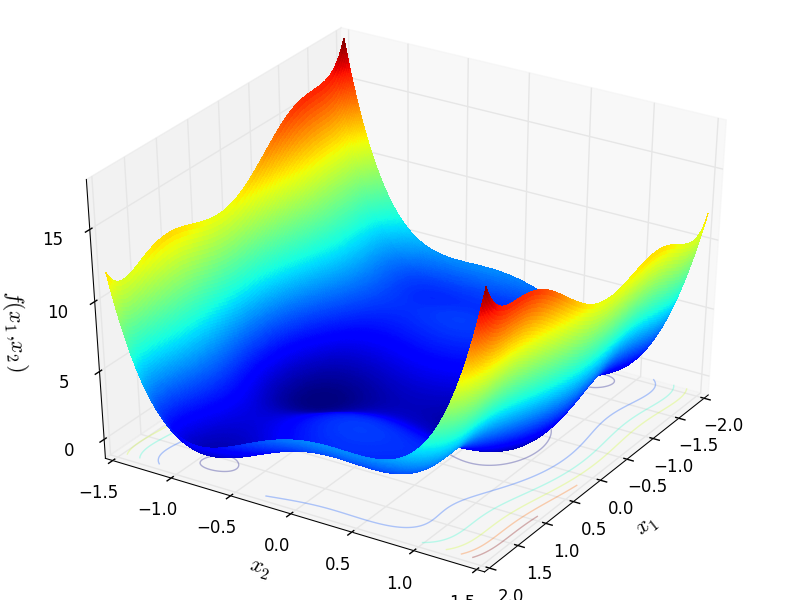
Two-dimensional SixHumpCamel function
Global optimum: 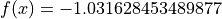 for
for
![x = [0.08984201368301331 , -0.7126564032704135]](_images/math/ea4d5f0068df9f42c3c8b49a9f94f0a65a659bd1.png) or
or
![x = [-0.08984201368301331, 0.7126564032704135]](_images/math/d34af529cf15b0d0bf9988ae2449f5ea74475f32.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Sodp objective function.
This class defines the Sum Of Different Powers global optimization problem. This is a multimodal minimization problem defined as follows:
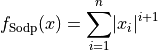
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
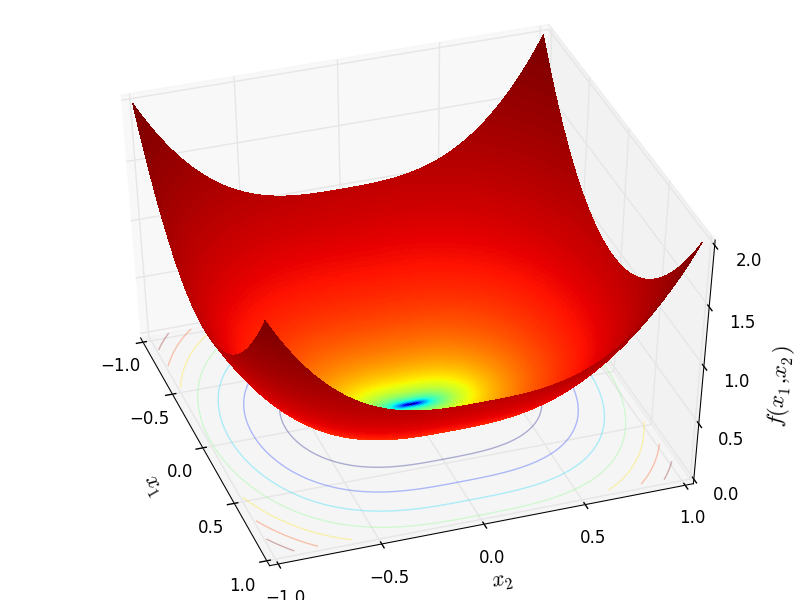
Two-dimensional Sodp function
Global optimum:  for
for 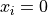 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Sphere objective function.
This class defines the Sphere global optimization problem. This is a multimodal minimization problem defined as follows:
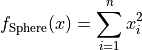
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
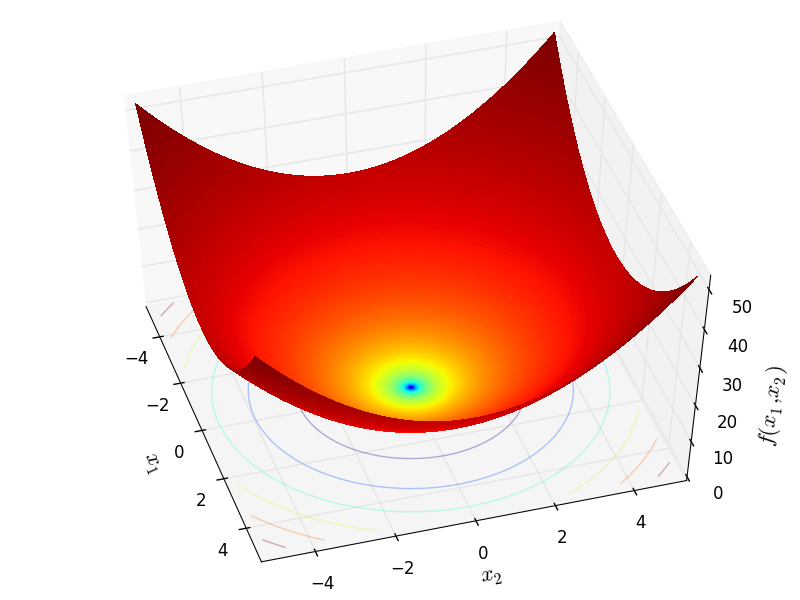
Two-dimensional Sphere function
Global optimum:  for
for 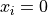 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil has stupid limits
SphericalSinc objective function.
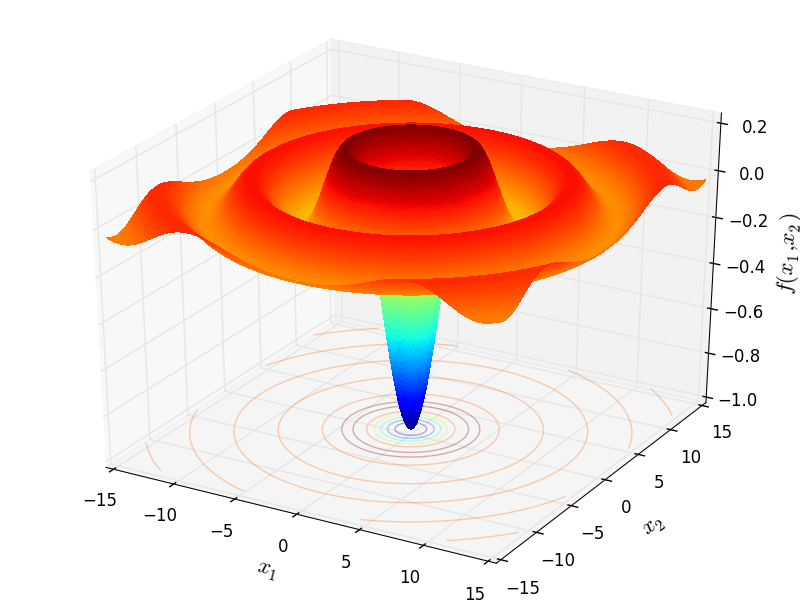
Two-dimensional SphericalSinc function
Spike objective function.
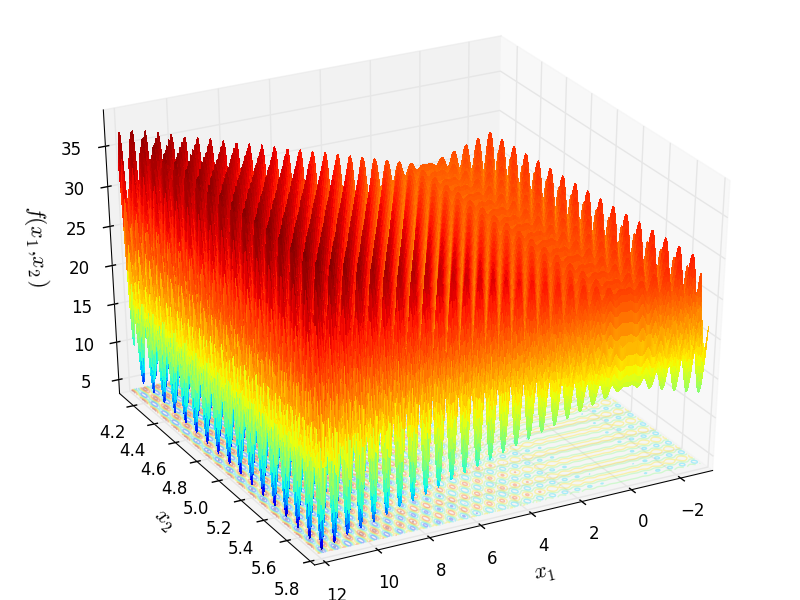
Two-dimensional Spike function
Step objective function.
This class defines the Step global optimization problem. This is a multimodal minimization problem defined as follows:
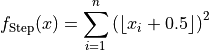
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
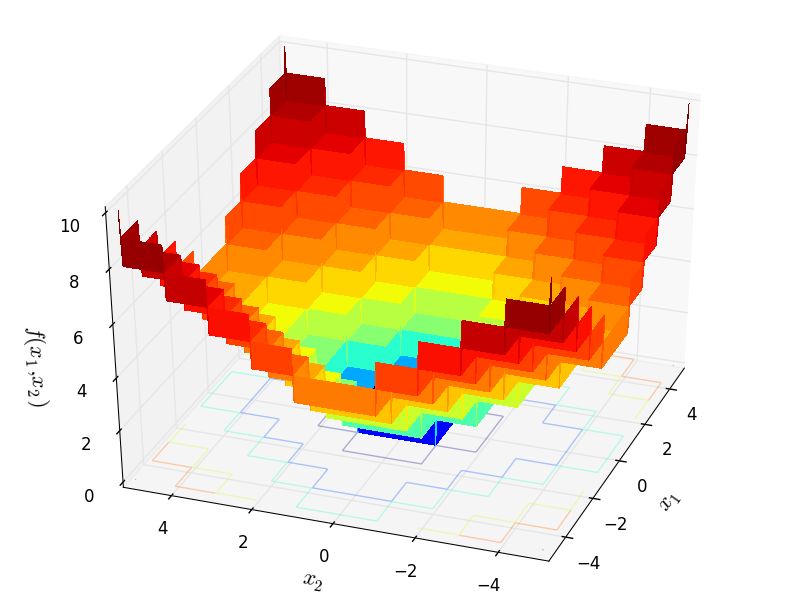
Two-dimensional Step01 function
Global optimum:  for
for 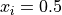 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Step objective function.
This class defines the Step 2 global optimization problem. This is a multimodal minimization problem defined as follows:
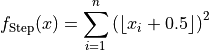
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
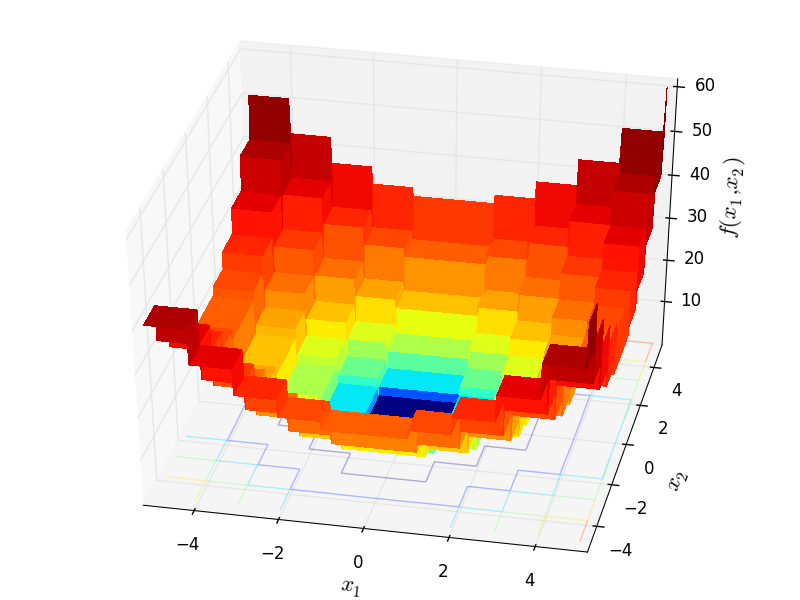
Two-dimensional Step02 function
Global optimum:  for
for 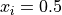 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Step 3 objective function.
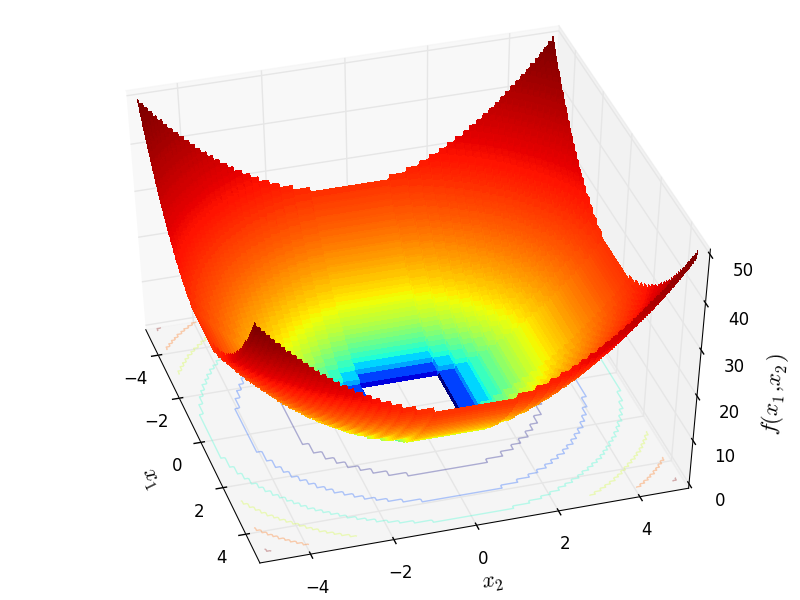
Two-dimensional Step03 function
Stochastic objective function.
This class defines the Stochastic global optimization problem. This is a multimodal minimization problem defined as follows:
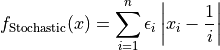
The variable 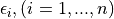 is a random variable uniformly
distributed in
is a random variable uniformly
distributed in ![[0, 1]](_images/math/ab178d831a786b92cb4c9ddc2d33578223036f98.png) .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
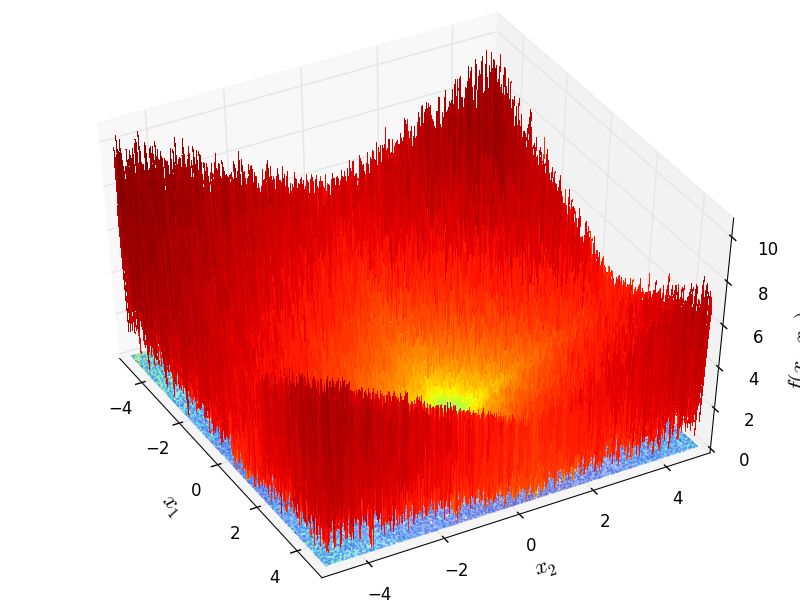
Two-dimensional Stochastic function
Global optimum:  for
for ![x_i = [1/n]](_images/math/076d6bda9c86979a469a0054ee62a82c3b20eefc.png) for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
StretchedV objective function.
This class defines the Stretched V global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{StretchedV}}(x) = \sum_{i=1}^{n-1} t^{1/4}
[\sin (50t^{0.1}) + 1]^2](_images/math/cd3a2fa50a17245f503d672a540650647eed74d2.png)
Where, in this exercise:
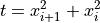
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
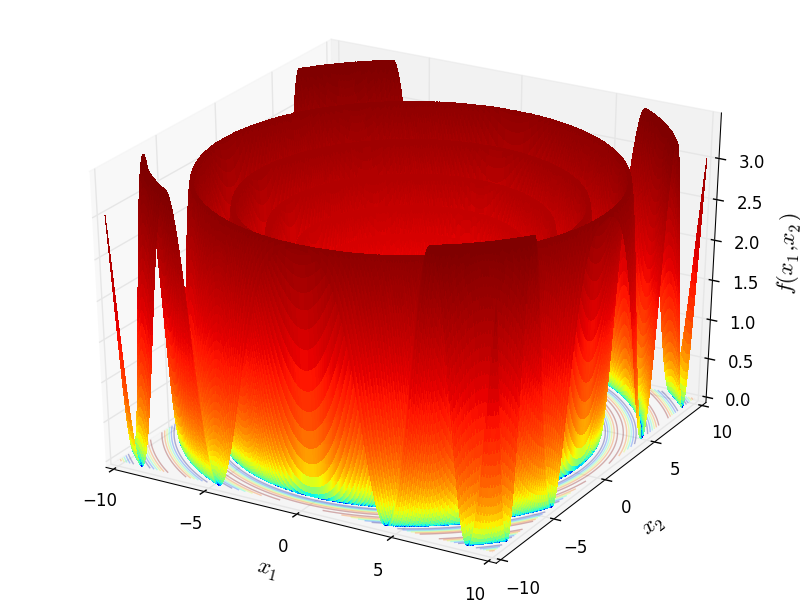
Two-dimensional StretchedV function
Global optimum:  for
for ![x = [0., 0.]](_images/math/5ad0062747a7364d89c2a032290b00e70f3a53b7.png) when
when
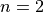 .
.
Adorio, E. MVF - “Multivariate Test Functions Library in C for Unconstrained Global Optimization”, 2005
Todo
All the sources disagree on the equation, in some the 1 is in the brackets, in others it is outside. In Jamil#142 it’s not even 1. Here we go with the Adorio option.
StyblinskiTang objective function.
This class defines the Styblinski-Tang global optimization problem. This is a multimodal minimization problem defined as follows:
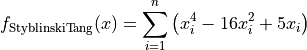
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
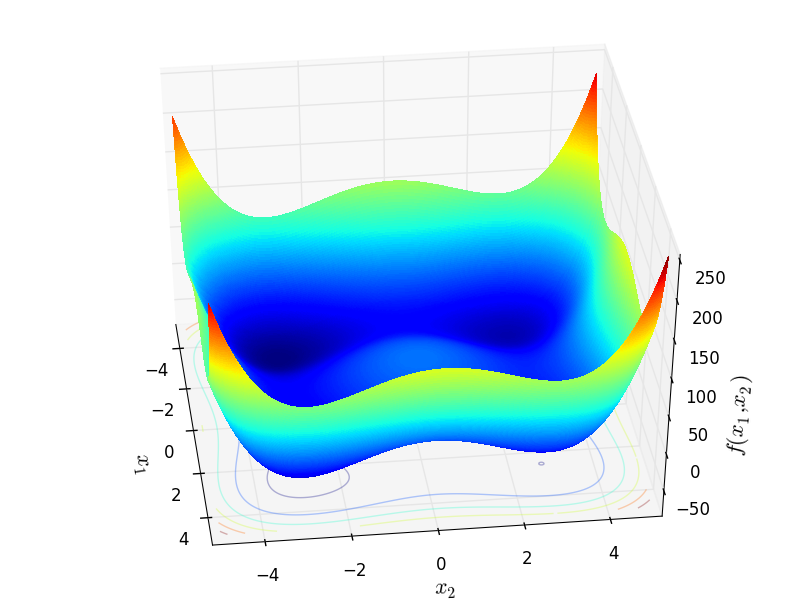
Two-dimensional StyblinskiTang function
Global optimum: 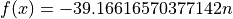 for
for
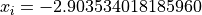 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.