Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions R
 N-D Test Functions R¶
N-D Test Functions R¶Rana objective function.
This class defines the Rana global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rana}}(x) = \sum_{i=1}^{n} \left[x_{i}
\sin\left(\sqrt{\lvert{x_{1} - x_{i} + 1}\rvert}\right)
\cos\left(\sqrt{\lvert{x_{1} + x_{i} + 1}\rvert}\right) +
\left(x_{1} + 1\right) \sin\left(\sqrt{\lvert{x_{1} + x_{i} +
1}\rvert}\right) \cos\left(\sqrt{\lvert{x_{1} - x_{i} +
1}\rvert}\right)\right]](_images/math/3df18b89478db2398b997191f1d295da2be84a04.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-512.0, 512.0]](_images/math/0171b1e07238a49c9f249d17fee4cf45089285b0.png) for
for  .
.
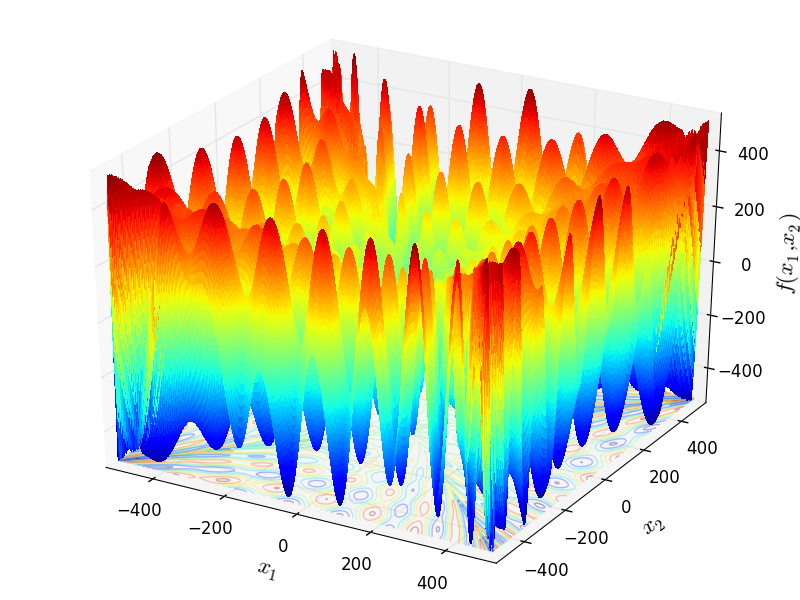
Two-dimensional Rana function
Global optimum:  for
for
![x = [-300.3376, 500]](_images/math/bc65e11b5197c01b57f35b6f5a7a5f5b0a8e22fa.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
homemade global minimum here.
Rastrigin objective function.
This class defines the Rastrigin global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rastrigin}}(x) = 10n \sum_{i=1}^n \left[ x_i^2
- 10 \cos(2\pi x_i) \right]](_images/math/a34a8418cd50fd1189796935c1afbb65885bf732.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.
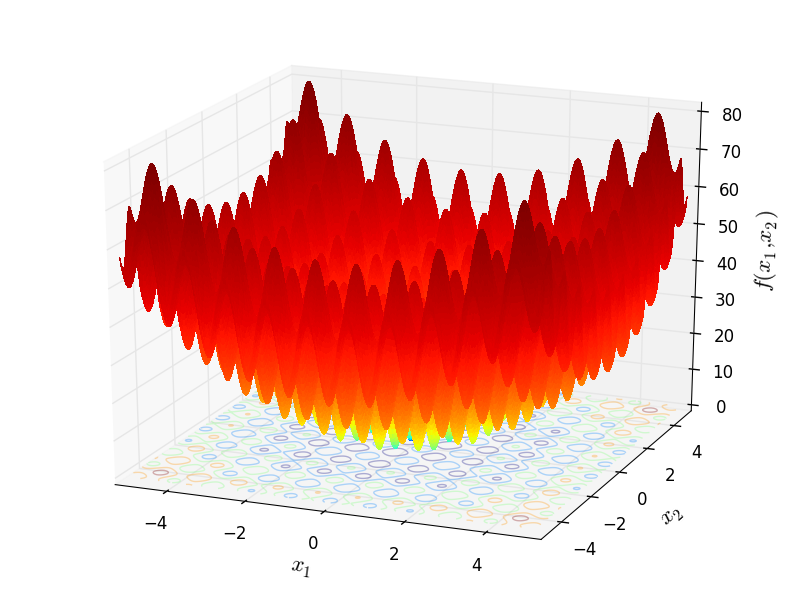
Two-dimensional Rastrigin function
Global optimum:  for
for 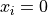 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Ratkowsky objective function.
http://www.itl.nist.gov/div898/strd/nls/data/ratkowsky3.shtml
Todo
this is a NIST regression standard dataset
Ratkowsky02 objective function.
This class defines the Ratkowsky 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Ratkowsky02}}(x) = \sum_{m=1}^{9}(a_m - x[0] / (1 + exp(x[1]
- b_m x[2]))^2](_images/math/9197cc273c5f6e508b3d121574810bef54a1eecb.png)
where
![\begin{cases}
a=[8.93, 10.8, 18.59, 22.33, 39.35, 56.11, 61.73, 64.62, 67.08] \\
b=[9., 14., 21., 28., 42., 57., 63., 70., 79.] \\
\end{cases}](_images/math/65c6fbe02025eb93f6407d6d40e7f265eb8f6faf.png)
Here ![x_1\in [1, 100]](_images/math/05a41dc58bfc0c422fed07ada2b9e36ad04f139c.png) ,
, ![x_2\in [0.1, 5]](_images/math/2042713bf1d89db26ff93242f561b8c15d992f09.png) and
and
![x_3\in [0.01, 0.5]](_images/math/0a835efb213f42a106c02327e398457dedaf7f49.png)
Global optimum: 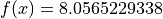 for
for
![x = [7.2462237576e1, 2.6180768402, 6.7359200066e-2]](_images/math/c427f22cc88e777dfdeea4c52272805757ed413a.png)
http://www.itl.nist.gov/div898/strd/nls/data/ratkowsky2.shtml
ReduxSum objective function.
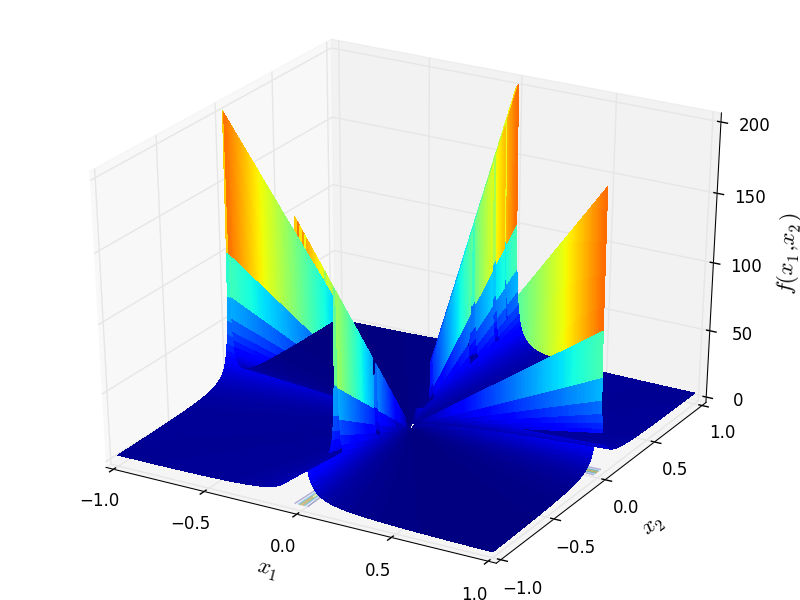
Two-dimensional ReduxSum function
Ripple 1 objective function.
This class defines the Ripple 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Ripple01}}(x) = \sum_{i=1}^2 -e^{-2 \log 2
(\frac{x_i-0.1}{0.8})^2} \left[\sin^6(5 \pi x_i)
+ 0.1\cos^2(500 \pi x_i) \right]](_images/math/c63bd85201b316174fbb3559c9a0833bb1ce2888.png)
with ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
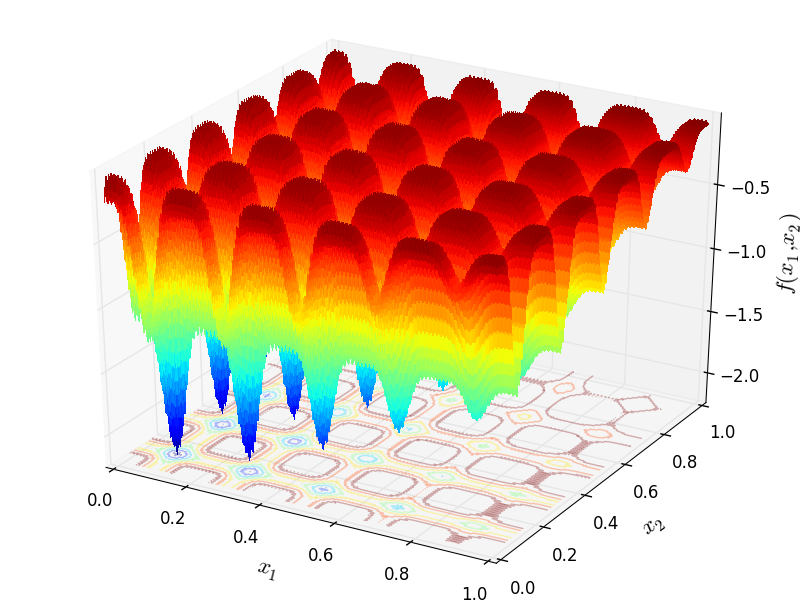
Two-dimensional Ripple01 function
Global optimum: 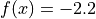 for
for 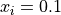 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Ripple 25 objective function.
This class defines the Ripple 25 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Ripple25}}(x) = \sum_{i=1}^2 -e^{-2
\log 2 (\frac{x_i-0.1}{0.8})^2}
\left[\sin^6(5 \pi x_i) \right]](_images/math/ab1d3db87646b205a34a74623100a057c95b855d.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
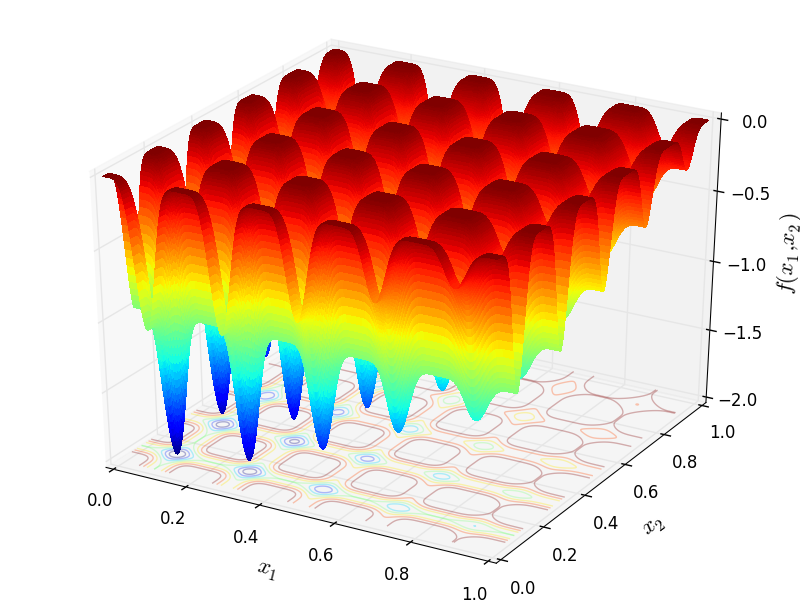
Two-dimensional Ripple25 function
Global optimum: 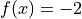 for
for 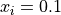 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Rosenbrock objective function.
This class defines the Rosenbrock global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rosenbrock}}(x) = \sum_{i=1}^{n-1} [100(x_i^2
- x_{i+1})^2 + (x_i - 1)^2]](_images/math/0168e249a4ea9b5170e48aff07aa00f56ac87dc8.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-5, 10]](_images/math/98df04fbd9b8266181439af788bf1880288e02c8.png) for
for  .
.
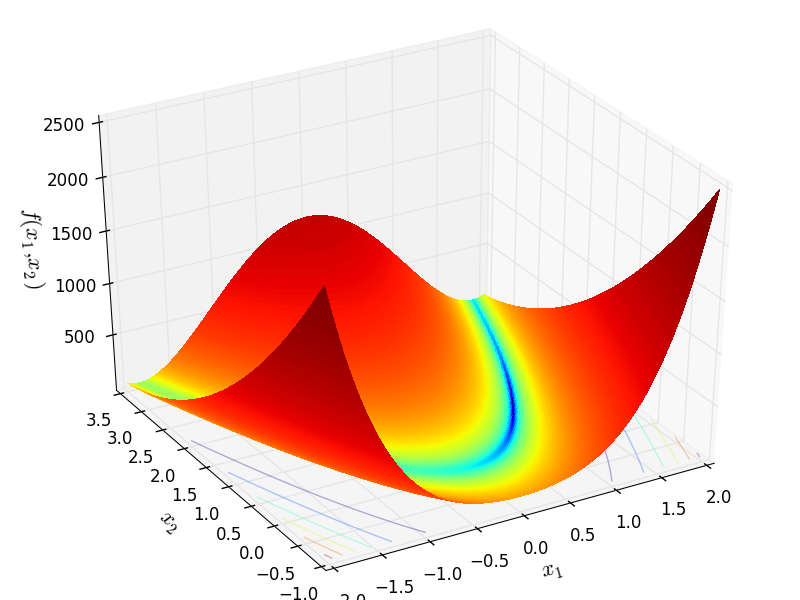
Two-dimensional Rosenbrock function
Global optimum:  for
for 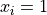 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
RosenbrockDisc objective function.
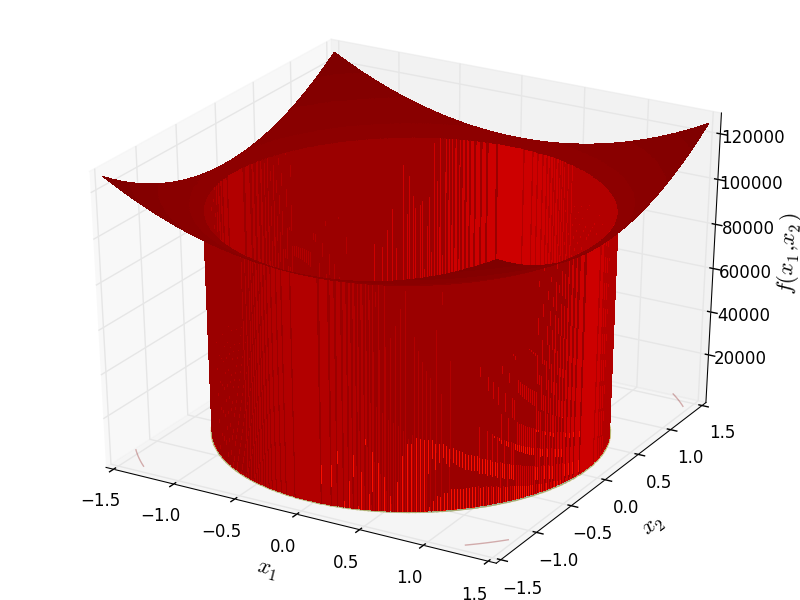
Two-dimensional RosenbrockDisc function
Modified Rosenbrock objective function.
This class defines the Modified Rosenbrock global optimization problem. This is a multimodal minimization problem defined as follows:
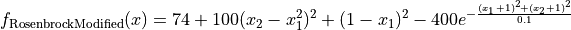
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-2, 2]](_images/math/3220cc226a0abf06f00e70257db97b5c754120f7.png) for
for  .
.
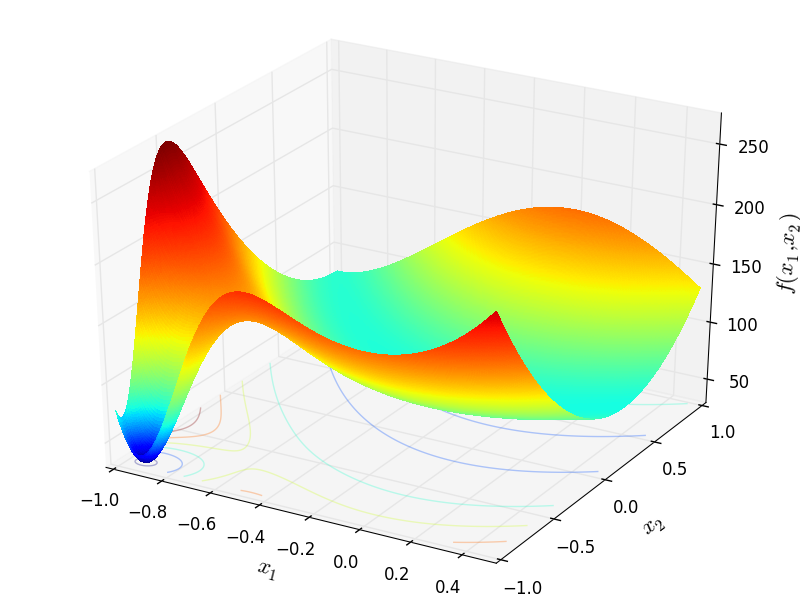
Two-dimensional RosenbrockModified function
Global optimum: 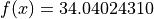 for
for
![x = [-0.90955374, -0.95057172]](_images/math/859989944c6dd240a651afd94ddd21b56b4f5838.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
We have different global minimum compared to Jamil #106. This is possibly because of the (1-x) term is using the wrong parameter.
Rotated Ellipse 1 objective function.
This class defines the Rotated Ellipse 1 global optimization problem. This is a unimodal minimization problem defined as follows:
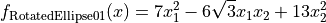
with ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
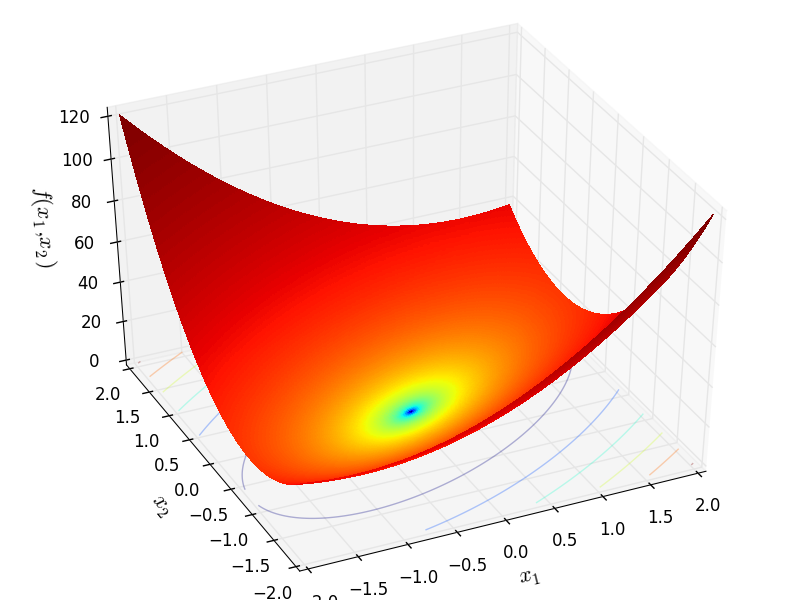
Two-dimensional RotatedEllipse01 function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Rotated Ellipse 2 objective function.
This class defines the Rotated Ellipse 2 global optimization problem. This is a unimodal minimization problem defined as follows:
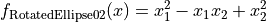
with ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
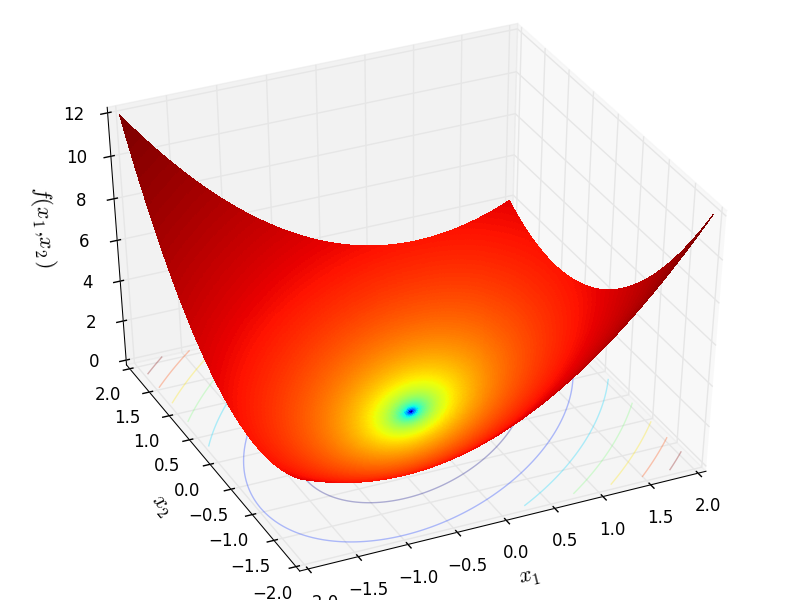
Two-dimensional RotatedEllipse02 function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.