N-D Test Functions U¶

class Ursem01(dimensions=2)¶

Ursem 1 objective function.

This class defines the Ursem 1 global optimization problem. This is a unimodal minimization problem defined as follows:

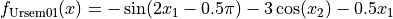
$f_{\text{Ursem01}}(x) = - \sin(2x_1 - 0.5 \pi) - 3 \cos(x_2) - 0.5 x_1$

with $x_1\in [-2.5, 3]$ and $x_2\in [-2, 2]$ .

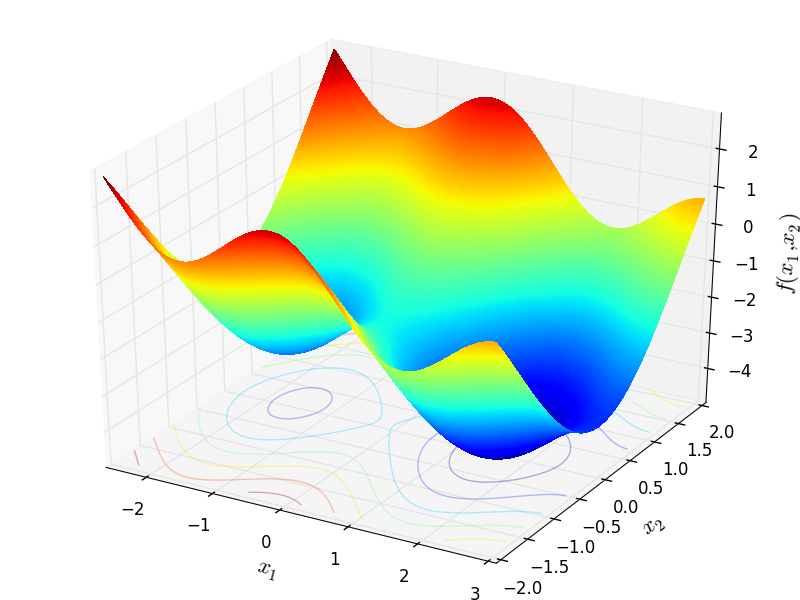
Two-dimensional Ursem01 function

Global optimum: 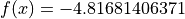$f(x) = -4.81681406371$ for $x = [1.69714, 0.0]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

class Ursem03(dimensions=2)¶

Ursem 3 objective function.

This class defines the Ursem 3 global optimization problem. This is a multimodal minimization problem defined as follows:

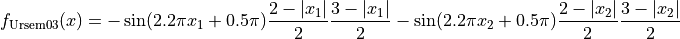
$f_{\text{Ursem03}}(x) = - \sin(2.2 \pi x_1 + 0.5 \pi) \frac{2 - \lvert x_1 \rvert}{2} \frac{3 - \lvert x_1 \rvert}{2} - \sin(2.2 \pi x_2 + 0.5 \pi) \frac{2 - \lvert x_2 \rvert}{2} \frac{3 - \lvert x_2 \rvert}{2}$

with $x_1\in [-2, 2]$ , $x_2\in [-1.5, 1.5]$ .

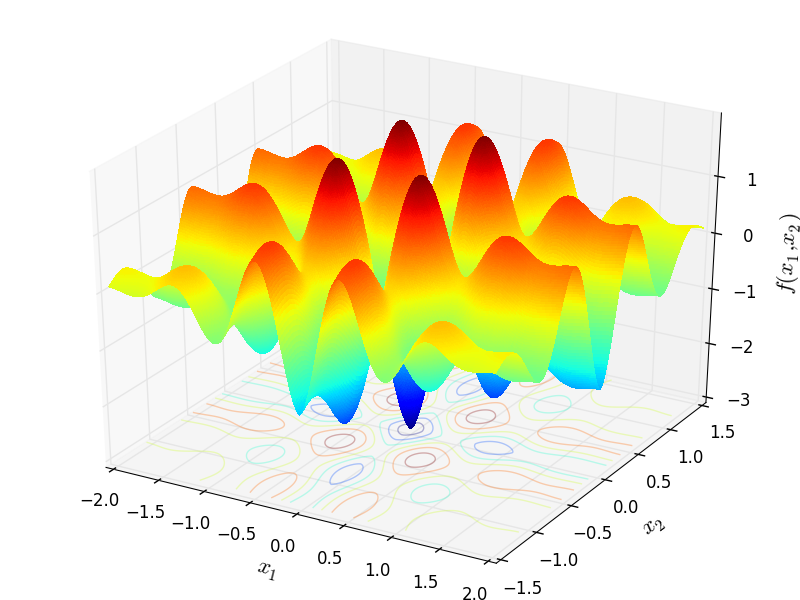
Two-dimensional Ursem03 function

Global optimum: 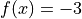$f(x) = -3$ for $x = [0, 0]$

Gavana, A. Global Optimization Benchmarks and AMPGO

Todo

Gavana and Jamil #157 disagree on the formulae here. Jamil squares the x[1] term in the sine expression. Gavana doesn’t. Go with Gavana here.

class Ursem04(dimensions=2)¶

Ursem 4 objective function.

This class defines the Ursem 4 global optimization problem. This is a multimodal minimization problem defined as follows:

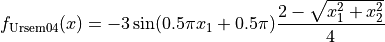
$f_{\text{Ursem04}}(x) = -3 \sin(0.5 \pi x_1 + 0.5 \pi) \frac{2 - \sqrt{x_1^2 + x_2 ^ 2}}{4}$

with $x_i \in [-2, 2]$ for $i = 1, 2$ .

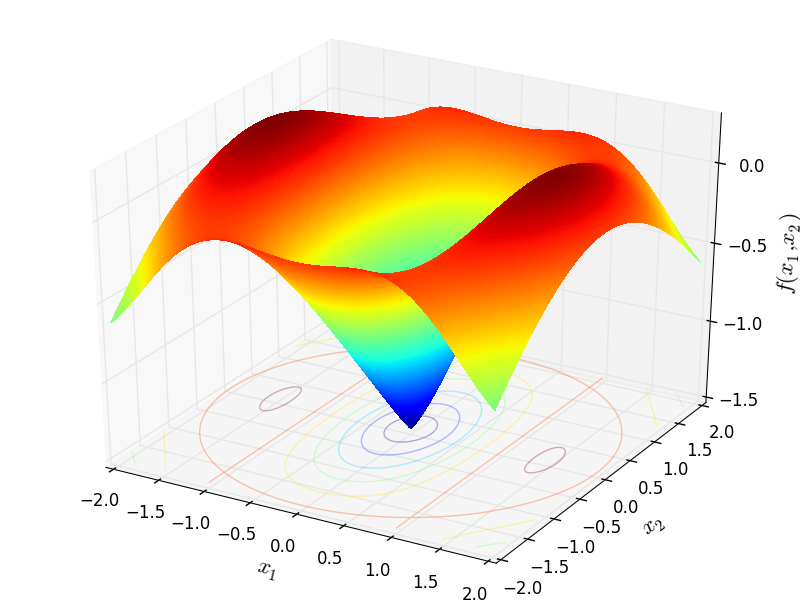
Two-dimensional Ursem04 function

Global optimum: 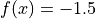$f(x) = -1.5$ for $x = [0, 0]$ for $i = 1, 2$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

class UrsemWaves(dimensions=2)¶

Ursem Waves objective function.

This class defines the Ursem Waves global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{UrsemWaves}}(x) = -0.9x_1^2 + (x_2^2 - 4.5x_2^2)x_1x_2 + 4.7 \cos \left[ 2x_1 - x_2^2(2 + x_1) \right ] \sin(2.5 \pi x_1)$

with $x_1\in [-0.9, 1.2]$ , $x_2\in [-1.2, 1.2]$ .

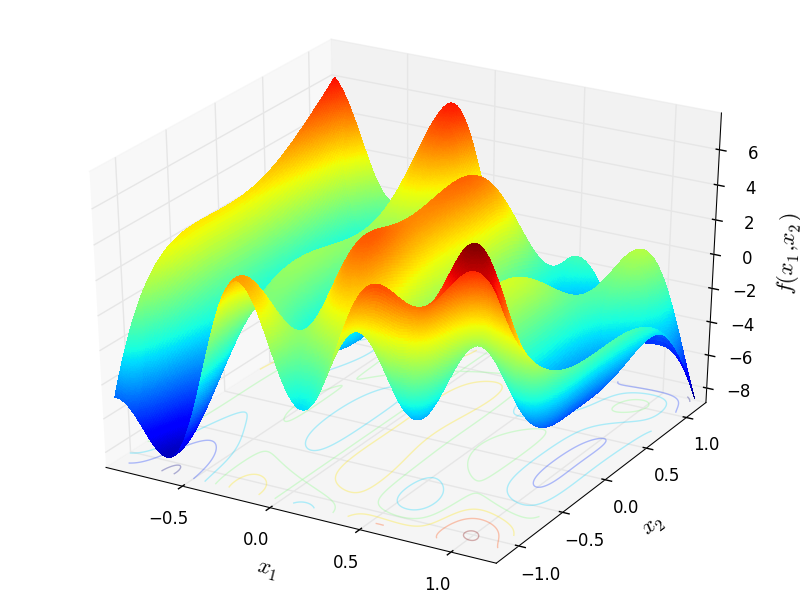
Two-dimensional UrsemWaves function

Global optimum: 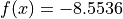$f(x) = -8.5536$ for $x = [1.2, 1.2]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

Todo

Jamil #159, has an x_2^2 - 4.5 x_2^2 in the brackets. Why wasn’t this rationalised to -5.5 x_2^2? This makes me wonder if the equation is listed correctly?

N-D Test Functions U¶

Previous topic

Next topic

This Page

Navigation

N-D Test Functions U¶

Previous topic

Next topic

This Page

Quick search

Navigation