N-D Test Functions V¶

class VenterSobiezcczanskiSobieski(dimensions=2)¶

Venter Sobiezcczanski-Sobieski objective function.

This class defines the Venter Sobiezcczanski-Sobieski global optimization problem. This is a multimodal minimization problem defined as follows:

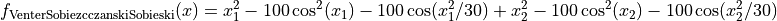
$f_{\text{VenterSobiezcczanskiSobieski}}(x) = x_1^2 - 100 \cos^2(x_1) - 100 \cos(x_1^2/30) + x_2^2 - 100 \cos^2(x_2) - 100 \cos(x_2^2/30)$

with $x_i \in [-50, 50]$ for $i = 1, 2$ .

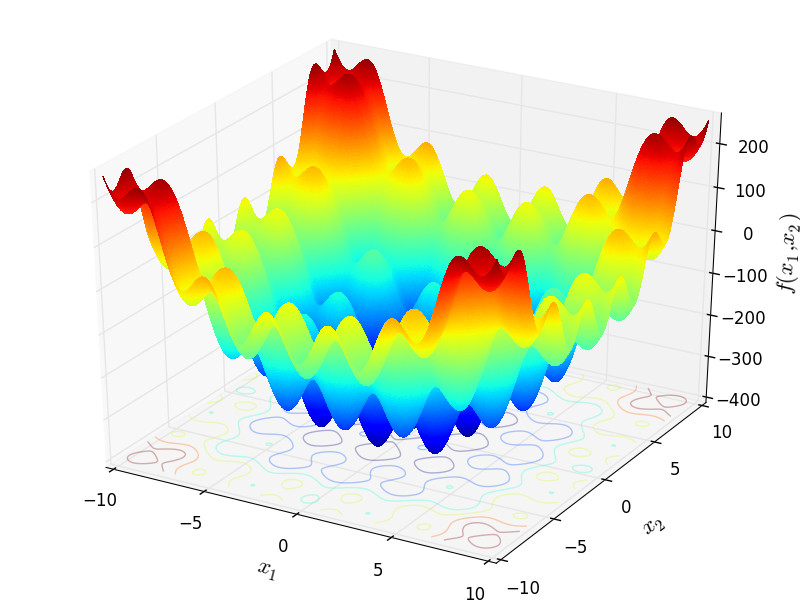
Two-dimensional VenterSobiezcczanskiSobieski function

Global optimum: 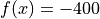$f(x) = -400$ for $x = [0, 0]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

Todo

Jamil #160 hasn’t written the equation very well. Normally a cos squared term is written as cos^2(x) rather than cos(x)^2

class Vincent(dimensions=2)¶

Vincent objective function.

This class defines the Vincent global optimization problem. This is a multimodal minimization problem defined as follows:

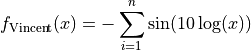
$f_{\text{Vincent}}(x) = - \sum_{i=1}^{n} \sin(10 \log(x))$

Here, $n$ represents the number of dimensions and $x_i \in [0.25, 10]$ for $i = 1, ..., n$ .

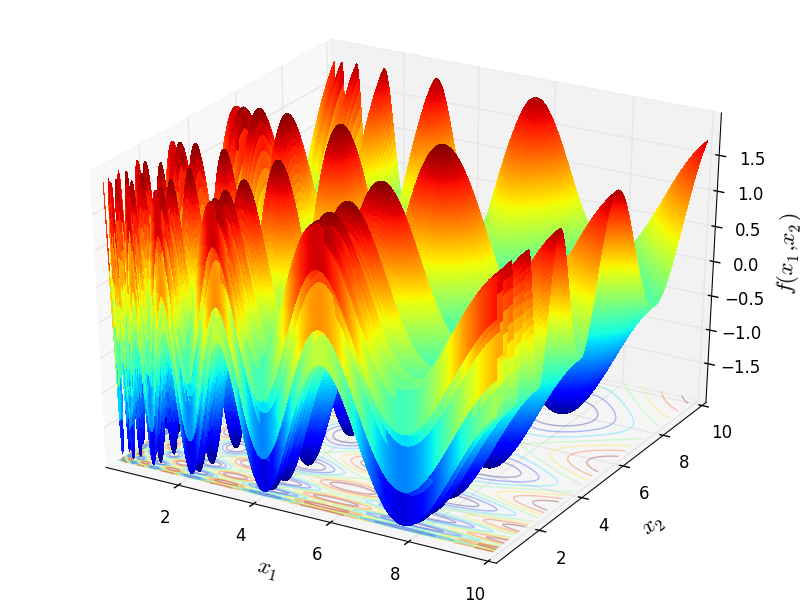
Two-dimensional Vincent function

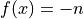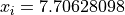Global optimum: $f(x) = -n$ for $x_i = 7.70628098$ for $i = 1, ..., n$

Gavana, A. Global Optimization Benchmarks and AMPGO

N-D Test Functions V¶

Previous topic

Next topic

This Page

Navigation

N-D Test Functions V¶

Previous topic

Next topic

This Page

Quick search

Navigation