Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions W
 N-D Test Functions W¶
N-D Test Functions W¶Watson objective function.
This class defines the Watson global optimization problem. This is a unimodal minimization problem defined as follows:
![f_{\text{Watson}}(x) = \sum_{i=0}^{29} \left\{
\sum_{j=0}^4 ((j + 1)a_i^j x_{j+1})
- \left[ \sum_{j=0}^5 a_i^j
x_{j+1} \right ]^2 - 1 \right\}^2
+ x_1^2](_images/math/70008b879917102121399ba8c58457cd526d8afc.png)
Where, in this exercise, 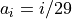 .
.
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for 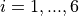 .
.
Global optimum: 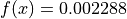 for
for
![x = [-0.0158, 1.012, -0.2329, 1.260, -1.513, 0.9928]](_images/math/f11746ee89b3c5ddfa674c554362be924c8f0640.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil #161 writes equation using (j - 1). According to code in Adorio and Gavana it should be (j+1). However the equations in those papers contain (j - 1) as well. However, I’ve got the right global minimum!!!
Wavy objective function.
This class defines the W / Wavy global optimization problem. This is a multimodal minimization problem defined as follows:
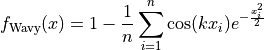
Where, in this exercise, 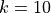 . The number of local minima is
. The number of local minima is
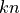 and
and 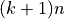 for odd and even
for odd and even  respectively.
respectively.
Here, ![x_i \in [-\pi, \pi]](_images/math/f3c18fa54f78b0fbb91f6c094697293de5e0b3f9.png) for
for  .
.
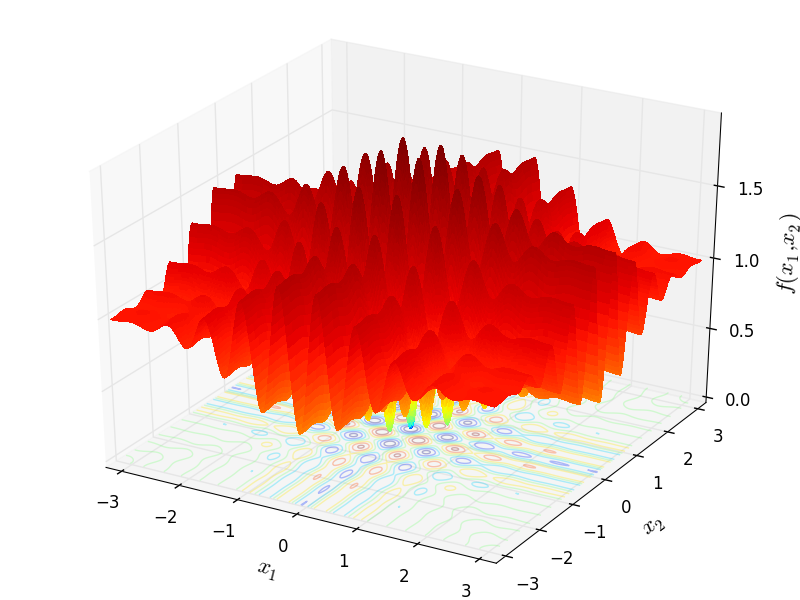
Two-dimensional Wavy function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Wayburn and Seader 1 objective function.
This class defines the Wayburn and Seader 1 global optimization problem. This is a unimodal minimization problem defined as follows:
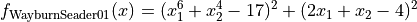
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
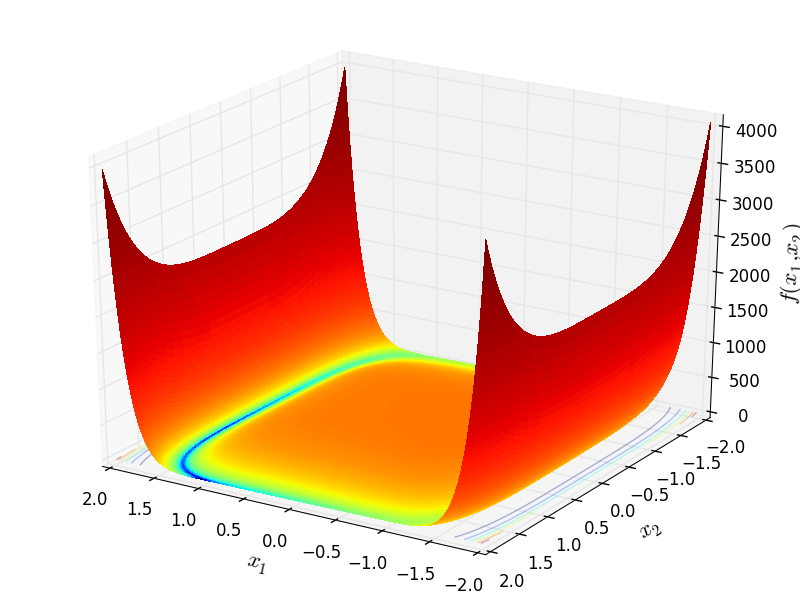
Two-dimensional WayburnSeader01 function
Global optimum:  for
for ![x = [1, 2]](_images/math/aa7c698cca12727616cab1c073b32e6390a4cb0a.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Wayburn and Seader 2 objective function.
This class defines the Wayburn and Seader 2 global optimization problem. This is a unimodal minimization problem defined as follows:
![f_{\text{WayburnSeader02}}(x) = \left[ 1.613 - 4(x_1 - 0.3125)^2
- 4(x_2 - 1.625)^2 \right]^2
+ (x_2 - 1)^2](_images/math/87a2cc8838601b779633c2fd9f2876c2c9404c05.png)
with ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
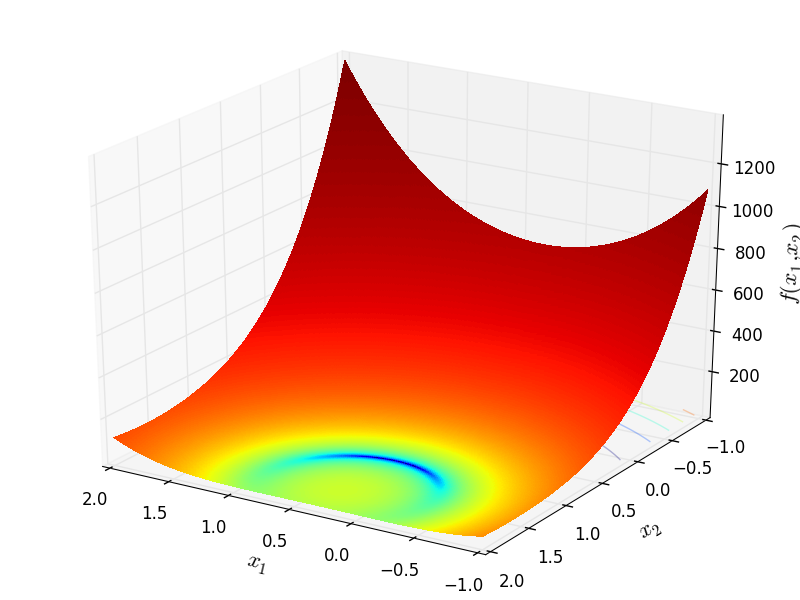
Two-dimensional WayburnSeader02 function
Global optimum:  for
for ![x = [0.2, 1]](_images/math/6b67ebe8fe0b2052011eb6fb95d4494fbb872a60.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Wayburn and Seader 3 objective function.
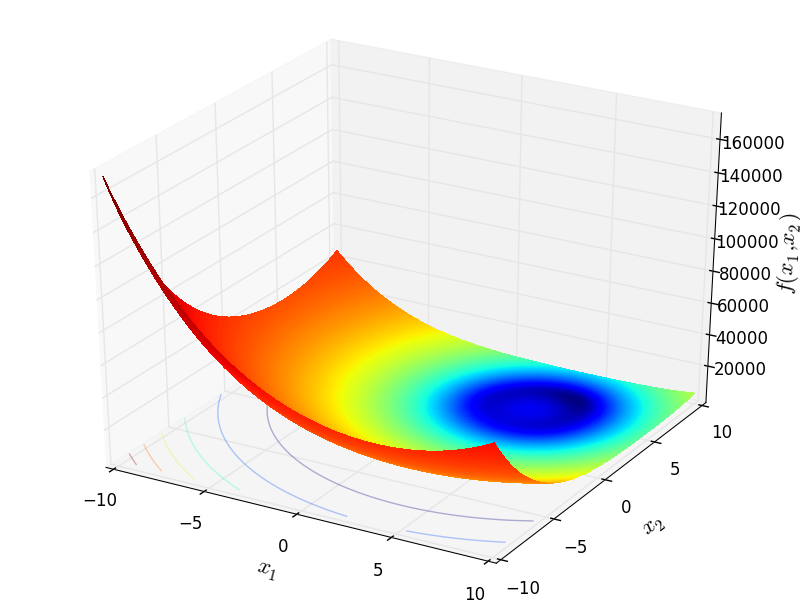
Two-dimensional WayburnSeader03 function
Weierstrass objective function.
This class defines the Weierstrass global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Weierstrass}}(x) = \sum_{i=1}^{n} \left [
\sum_{k=0}^{kmax} a^k \cos
\left( 2 \pi b^k (x_i + 0.5) \right) - n
\sum_{k=0}^{kmax} a^k \cos(\pi b^k) \right ]](_images/math/3d05f63a201df5743a4b106b0b83974649538c6c.png)
Where, in this exercise, 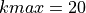 ,
, 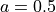 and
and
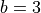 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-0.5, 0.5]](_images/math/95ff94da73788fc2234f6d2f9037e3c7df81a147.png) for
for  .
.
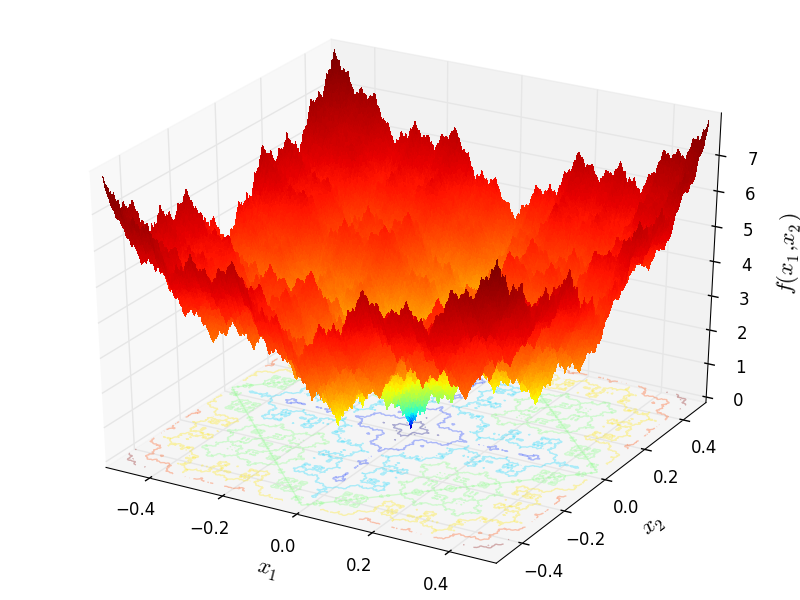
Two-dimensional Weierstrass function
Global optimum:  for
for 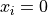 for
for

Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
Jamil, Gavana have got it wrong. The second term is not supposed to be included in the outer sum. Mishra code has it right as does the reference referred to in Jamil#166.
Whitley objective function.
This class defines the Whitley global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Whitley}}(x) = \sum_{i=1}^n \sum_{j=1}^n
\left[\frac{(100(x_i^2-x_j)^2
+ (1-x_j)^2)^2}{4000} - \cos(100(x_i^2-x_j)^2
+ (1-x_j)^2)+1 \right]](_images/math/23e762b82833c44bd046bf105cf60111f58b2893.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10.24, 10.24]](_images/math/3825846d98928e737251a1183cf6de356b0abc81.png) for
for  .
.
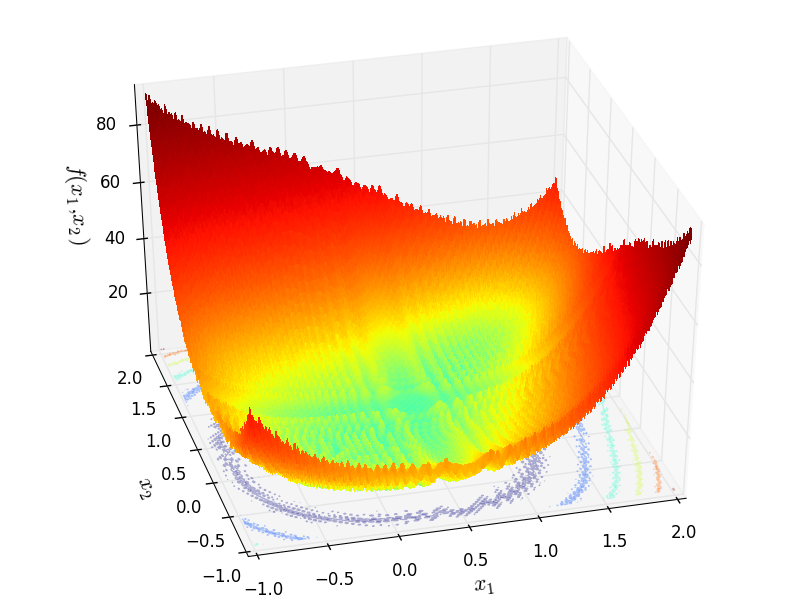
Two-dimensional Whitley function
Global optimum:  for
for 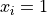 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Jamil#167 has ‘+ 1’ inside the cos term, when it should be outside it.
Wolfe objective function.
This class defines the Wolfe global optimization problem. This is a multimodal minimization problem defined as follows:
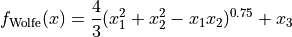
with ![x_i \in [0, 2]](_images/math/4ccbc8f05068478e57d7a9f37fccf74917eabaae.png) for
for 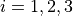 .
.
Global optimum:  for
for ![x = [0, 0, 0]](_images/math/084071b51d8f3dff31e8aa7becc26d7baeb4fbe8.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.