Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions K
 N-D Test Functions K¶
N-D Test Functions K¶Katsuura objective function.
This class defines the Katsuura global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Katsuura}}(x) = \prod_{i=0}^{n-1} \left [ 1 +
(i+1) \sum_{k=1}^{d} \lfloor (2^k x_i) \rfloor 2^{-k} \right ]](_images/math/6abc34f37c5fec119498da63e86559d890f28851.png)
Where, in this exercise, 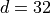 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [0, 100]](_images/math/dff6d980169d585461c8b4dce088b6e71c019f70.png) for
for  .
.
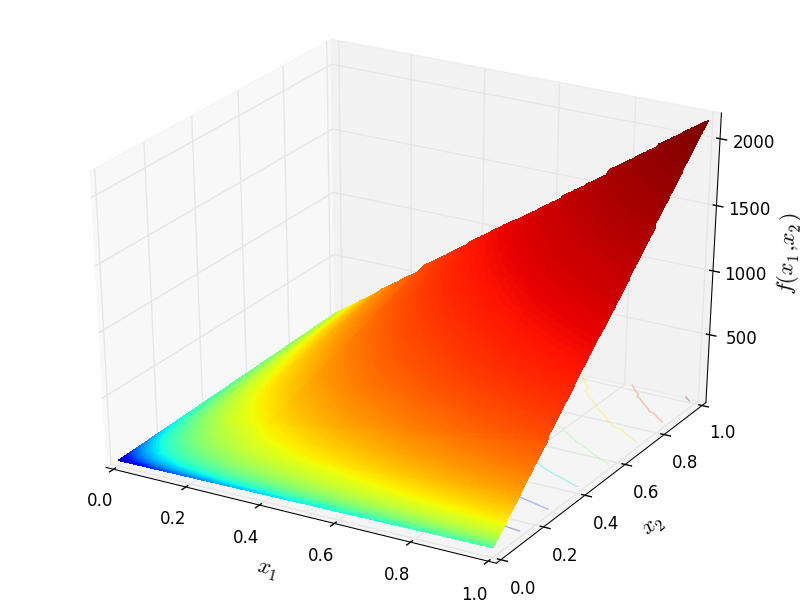
Two-dimensional Katsuura function
Global optimum: 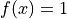 for
for 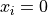 for
for
 .
.
Adorio, E. MVF - “Multivariate Test Functions Library in C for Unconstrained Global Optimization”, 2005 Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Adorio has wrong global minimum. Adorio uses round, Gavana docstring uses floor, but Gavana code uses round. We’ll use round...
Keane objective function.
This class defines the Keane global optimization problem. This is a multimodal minimization problem defined as follows:
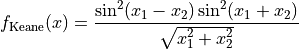
with ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
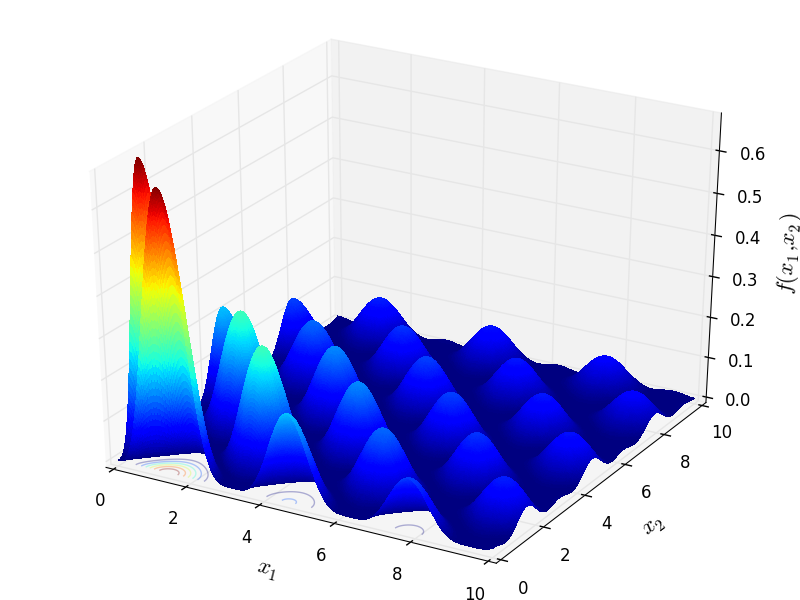
Two-dimensional Keane function
Global optimum: 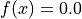 for
for
![x = [7.85396153, 7.85396135]](_images/math/566c7bc85897004a055e7087b2b50fb518403e2f.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil #69, there is no way that the function can have a negative value. Everything is squared. I think that they have the wrong solution.
Kearfott Cosine objective function.
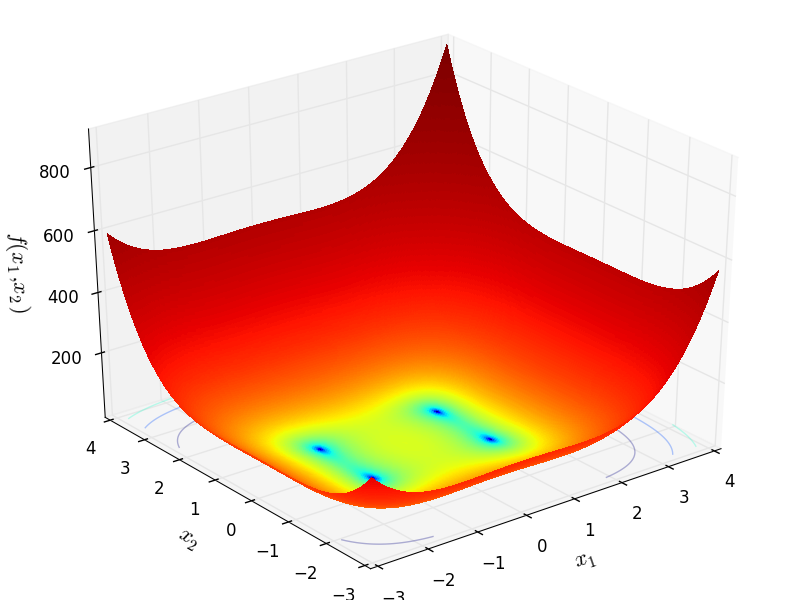
Two-dimensional Kearfott function
Kowalik objective function.
This class defines the Kowalik global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Kowalik}}(x) = \sum_{i=0}^{10} \left [ a_i
- \frac{x_1 (b_i^2 + b_i x_2)} {b_i^2 + b_i x_3 + x_4} \right ]^2](_images/math/36a3f81f01fd000f6bd3805cbb740b86c0a9a610.png)
Where:
![\begin{matrix}
a = [4, 2, 1, 1/2, 1/4 1/8, 1/10, 1/12, 1/14, 1/16] \\
b = [0.1957, 0.1947, 0.1735, 0.1600, 0.0844, 0.0627, 0.0456, 0.0342, 0.0323, 0.0235, 0.0246] \\
\end{matrix}](_images/math/e08c15d709f2f586bd621dba13bebc2ec3ca4d1e.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in
[-5, 5]](_images/math/ec0d489a126d2ef590d4bf8ff07e7b40ed85a42f.png) for
for 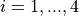 .
.
Global optimum: 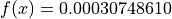 for
for ![x =
[0.192833, 0.190836, 0.123117, 0.135766]](_images/math/e5906d516fb4975324f6669651adde51e3810ebc.png) .
.