Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions J
 N-D Test Functions J¶
N-D Test Functions J¶Jennrich-Sampson objective function.
This class defines the Jennrich-Sampson global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{JennrichSampson}}(x) = \sum_{i=1}^{10} \left [2 + 2i
- (e^{ix_1} + e^{ix_2}) \right ]^2](_images/math/afe7aeae5958ead3f2028619f2bfaee4a194b234.png)
with ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
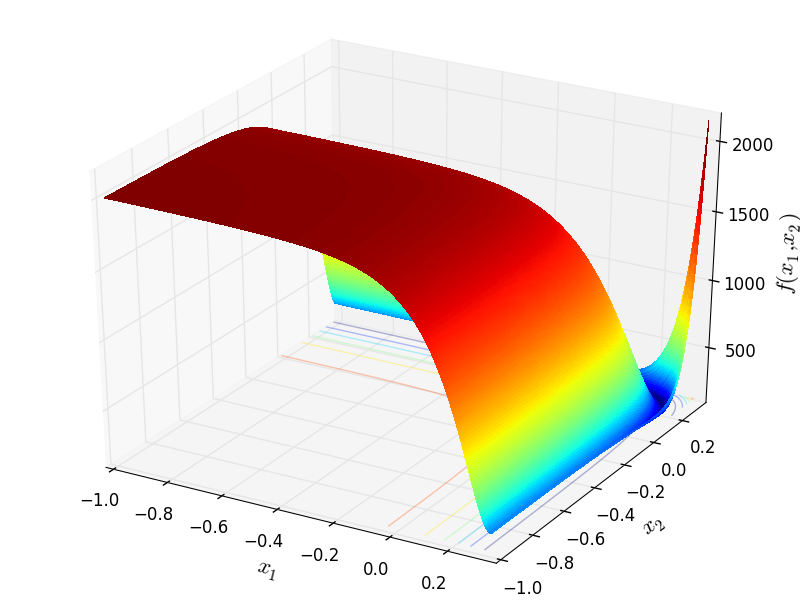
Two-dimensional JennrichSampson function
Global optimum:  for
for
![x = [0.257825, 0.257825]](_images/math/1fe8b59e907f5f6d4d6365914ab6f5a198745015.png) .
.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Judge objective function.
This class defines the Judge global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Judge}}(x) = \sum_{i=1}^{20}
\left [ \left (x_1 + A_i x_2 + B x_2^2 \right ) - C_i \right ]^2](_images/math/53d46ead50f2a3d6698c50e76cd56d0b14094a8a.png)
Where, in this exercise:
![\begin{cases}
A = [0.286, 0.973, 0.384, 0.276, 0.973, 0.543, 0.957, 0.948, 0.543, 0.797, 0.936, 0.889, 0.006, 0.828, 0.399, 0.617, 0.939, 0.784, 0.072, 0.889] \\
B = [0.645, 0.585, 0.310, 0.058, 0.455, 0.779, 0.259, 0.202, 0.028, 0.099, 0.142, 0.296, 0.175, 0.180, 0.842, 0.039, 0.103, 0.620, 0.158, 0.704] \\
C = [4.284, 4.149, 3.877, 0.533, 2.211, 2.389, 2.145, 3.231, 1.998, 1.379, 2.106, 1.428, 1.011, 2.179, 2.858, 1.388, 1.651, 1.593, 1.046, 2.152]
\end{cases}](_images/math/3554245511b740e8364adceeaaf07f1b9e59c04f.png)
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
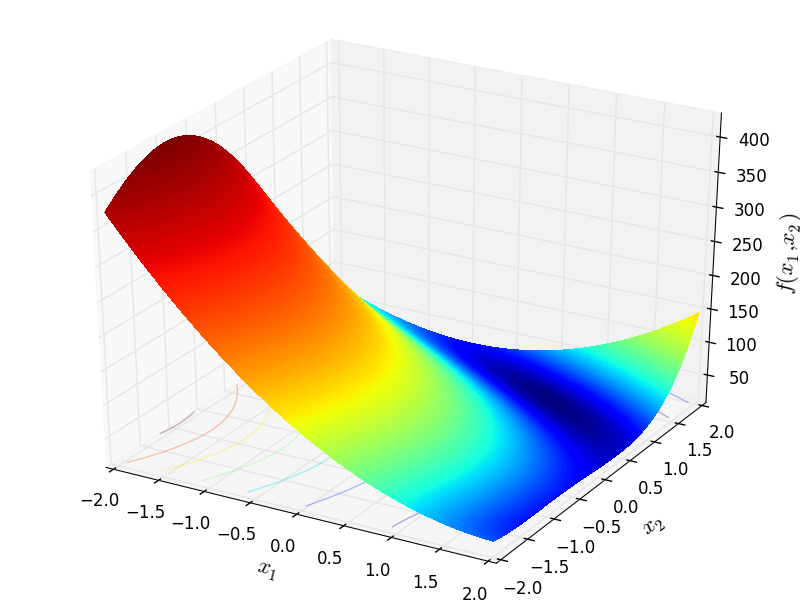
Two-dimensional Judge function
Global optimum: 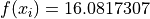 for
for
![\mathbf{x} = [0.86479, 1.2357]](_images/math/e2b4ee53b58524806818812e93640e51eff4dd8c.png) .
.
Gavana, A. Global Optimization Benchmarks and AMPGO