Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions G
 N-D Test Functions G¶
N-D Test Functions G¶Gear objective function.
This class defines the Gear global optimization problem. This is a multimodal minimization problem defined as follows:
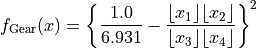
with ![x_i \in [12, 60]](_images/math/dede825b8eb6d5fc4458fe32630b03f0e24b49f1.png) for
for 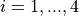 .
.
Global optimum: 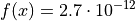 for
for ![x =
[16, 19, 43, 49]](_images/math/de22b6d8f13d4b0b23ef2a204ba05bed32461a07.png) , where the various
, where the various 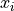 may be permuted.
may be permuted.
Gavana, A. Global Optimization Benchmarks and AMPGO
Giunta objective function.
This class defines the Giunta global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Giunta}}({x}) = 0.6 + \sum_{i=1}^{n} \left[\sin^{2}\left(1
- \frac{16}{15} x_i\right) - \frac{1}{50} \sin\left(4
- \frac{64}{15} x_i\right) - \sin\left(1
- \frac{16}{15} x_i\right)\right]](_images/math/4374e558e6065677c2ee0afeaf9bd4cba642a2e1.png)
with ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
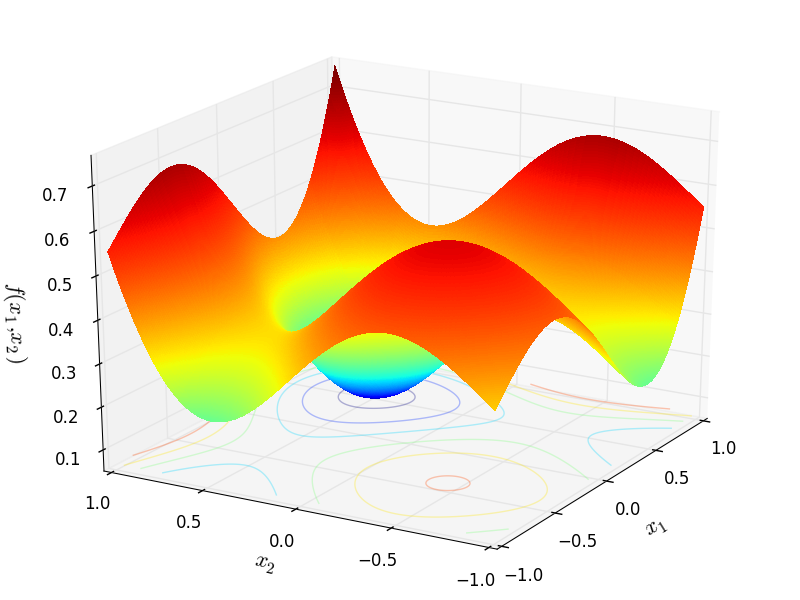
Two-dimensional Giunta function
Global optimum: 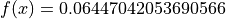 for
for
![x = [0.4673200277395354, 0.4673200169591304]](_images/math/89cb8452123689e3ee14273be49b54cddc46f18f.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
Jamil has the wrong fglob. I think there is a lower value.
Goldstein-Price objective function.
This class defines the Goldstein-Price global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{GoldsteinPrice}}(x) = \left[ 1 + (x_1 + x_2 + 1)^2
(19 - 14 x_1 + 3 x_1^2 - 14 x_2 + 6 x_1 x_2 + 3 x_2^2) \right]
\left[ 30 + ( 2x_1 - 3 x_2)^2 (18 - 32 x_1 + 12 x_1^2
+ 48 x_2 - 36 x_1 x_2 + 27 x_2^2) \right]](_images/math/3c53b30727dfc8fa219351bfa22e97658efea956.png)
with ![x_i \in [-2, 2]](_images/math/3220cc226a0abf06f00e70257db97b5c754120f7.png) for
for  .
.
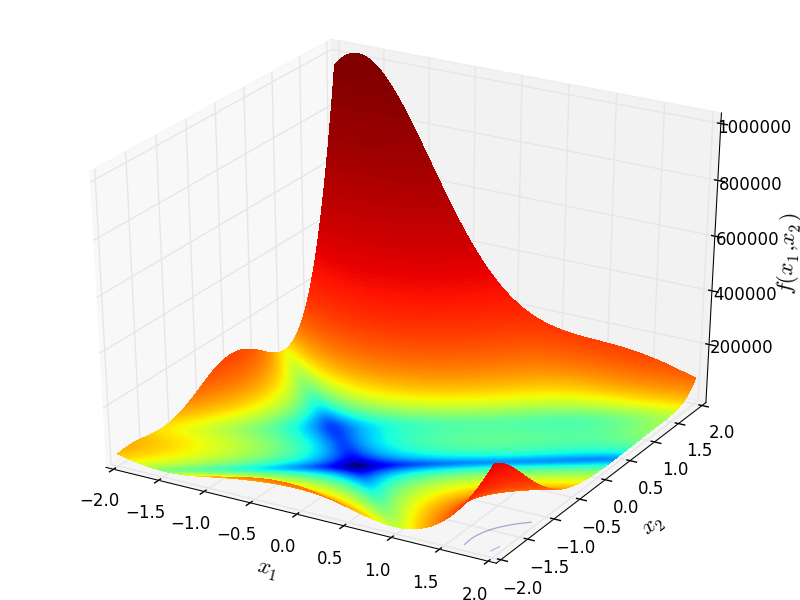
Two-dimensional GoldsteinPrice function
Global optimum: 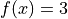 for
for ![x = [0, -1]](_images/math/68400534f0e7c91bc69e01ba40b0f700447e106e.png)
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Gramacy Lee objective function No 2.
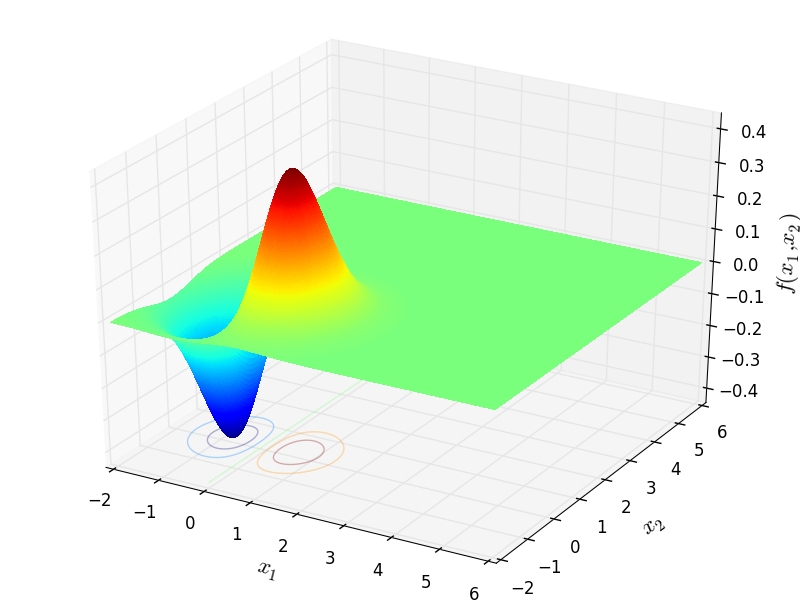
Two-dimensional GramacyLee02 function
Gramacy Lee objective function No 3.
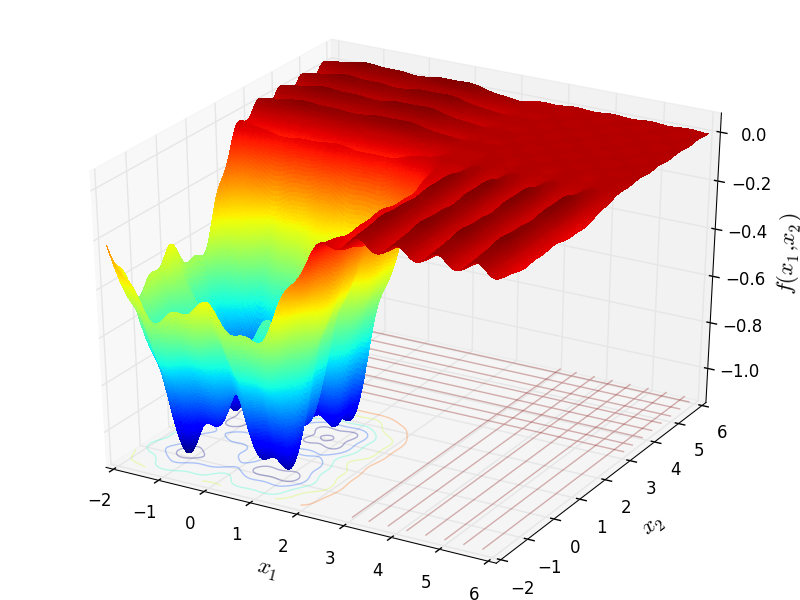
Two-dimensional GramacyLee03 function
Griewank objective function.
This class defines the Griewank global optimization problem. This is a multimodal minimization problem defined as follows:
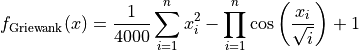
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-600, 600]](_images/math/0e2220a1d45e6496e4278b9191e14b72dbf2da2b.png) for
for  .
.
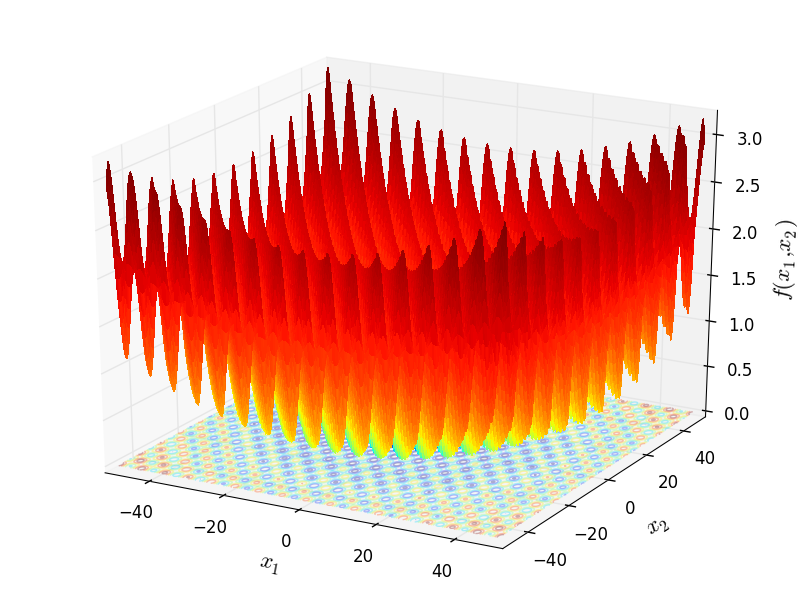
Two-dimensional Griewank function
Global optimum:  for
for 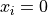 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Gulf objective function.
This class defines the Gulf global optimization problem. This is a multimodal minimization problem defined as follows:
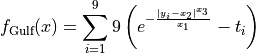
Where, in this exercise:
![t_i = i/100 \
y_i = 25 + [-50 \log(t_i)]^{2/3}](_images/math/39221cf69807e63b7d7fe6a258bf8eda957ef7c2.png)
with ![x_i \in [0, 60]](_images/math/96a3ee6ecb764ba6669d36899fea5c563488b3f5.png) for
for 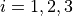 .
.
Global optimum:  for
for ![x = [50, 25, 1.5]](_images/math/c924032329378f153db4ead945f8e838bf77e361.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Todo
Gavana has absolute of (u - x[1]) term. Jamil doesn’t... Leaving it in.