N-D Test Functions H¶

class Hansen(dimensions=2)¶

Hansen objective function.

This class defines the Hansen global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Hansen}}(x) = \left[ \sum_{i=0}^4(i+1)\cos(ix_1+i+1)\right ] \left[\sum_{j=0}^4(j+1)\cos[(j+2)x_2+j+1])\right ]$

with $x_i \in [-10, 10]$ for $i = 1, 2$ .

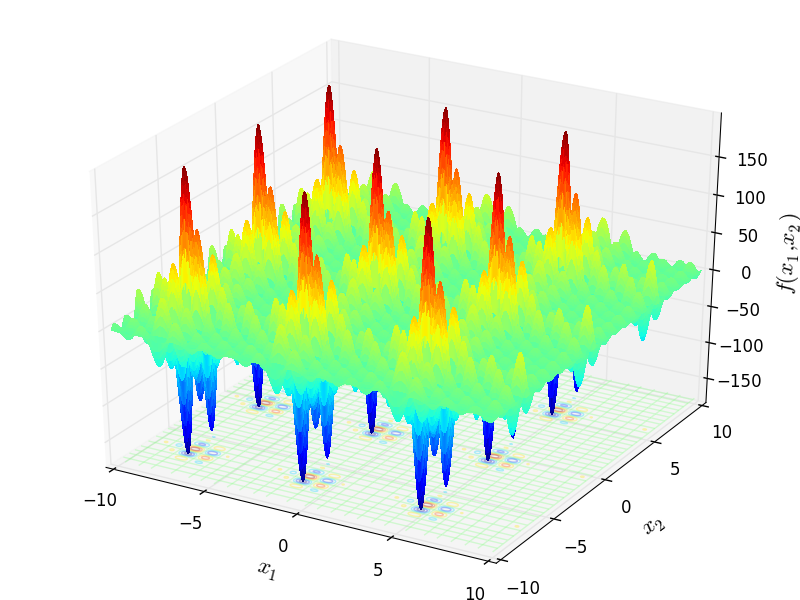
Two-dimensional Hansen function

Global optimum: 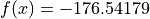$f(x) = -176.54179$ for $x = [-7.58989583, -7.70831466]$ .

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

Todo

Jamil #61 is missing the starting value of i.

class HappyCat(dimensions=2)¶: HappyCat objective function.

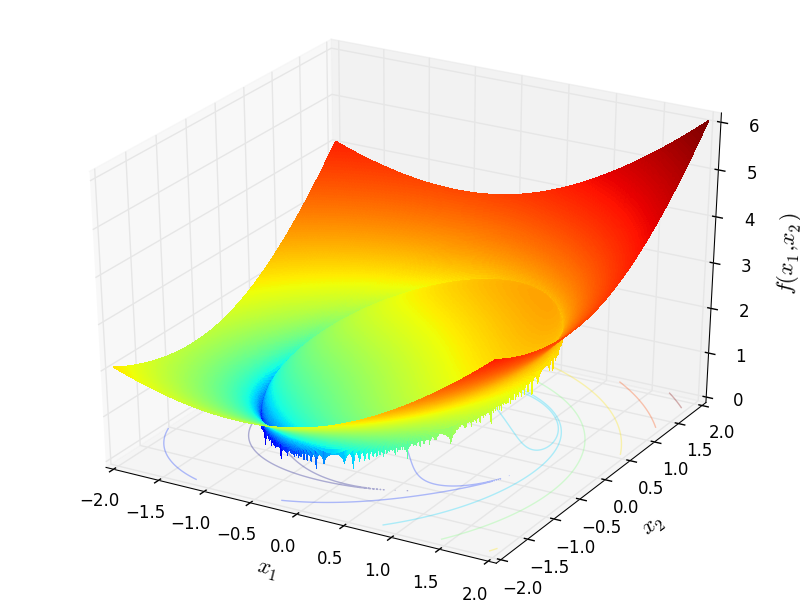
Two-dimensional HappyCat function

class Hartmann3(dimensions=3)¶

Hartmann3 objective function.

This class defines the Hartmann3 global optimization problem. This is a multimodal minimization problem defined as follows:

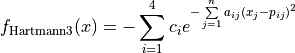
$f_{\text{Hartmann3}}(x) = -\sum\limits_{i=1}^{4} c_i e^{-\sum\limits_{j=1}^{n}a_{ij}(x_j - p_{ij})^2}$

Where, in this exercise:

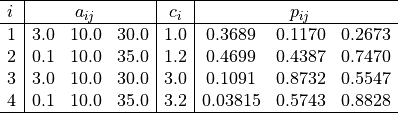
$\begin{array}{l|ccc|c|ccr} \hline i & & a_{ij}& & c_i & & p_{ij} & \\ \hline 1 & 3.0 & 10.0 & 30.0 & 1.0 & 0.3689 & 0.1170 & 0.2673 \\ 2 & 0.1 & 10.0 & 35.0 & 1.2 & 0.4699 & 0.4387 & 0.7470 \\ 3 & 3.0 & 10.0 & 30.0 & 3.0 & 0.1091 & 0.8732 & 0.5547 \\ 4 & 0.1 & 10.0 & 35.0 & 3.2 & 0.03815 & 0.5743 & 0.8828 \\ \hline \end{array}$

with $x_i \in [0, 1]$ for $i = 1, 2, 3$ .

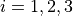Global optimum: 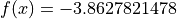$f(x) = -3.8627821478$ for $x = [0.11461292, 0.55564907, 0.85254697]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

Todo

Jamil #62 has an incorrect coefficient. p[1, 1] should be 0.4387

class Hartmann6(dimensions=6)¶

Hartmann6 objective function.

This class defines the Hartmann6 global optimization problem. This is a multimodal minimization problem defined as follows:

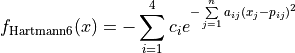
$f_{\text{Hartmann6}}(x) = -\sum\limits_{i=1}^{4} c_i e^{-\sum\limits_{j=1}^{n}a_{ij}(x_j - p_{ij})^2}$

Where, in this exercise:

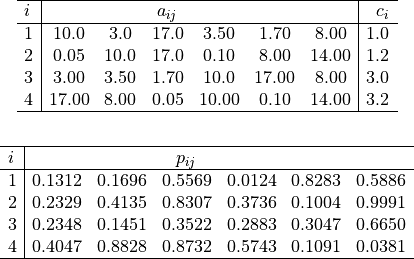
$\begin{array}{l|cccccc|r} \hline i & & & a_{ij} & & & & c_i \\ \hline 1 & 10.0 & 3.0 & 17.0 & 3.50 & 1.70 & 8.00 & 1.0 \\ 2 & 0.05 & 10.0 & 17.0 & 0.10 & 8.00 & 14.00 & 1.2 \\ 3 & 3.00 & 3.50 & 1.70 & 10.0 & 17.00 & 8.00 & 3.0 \\ 4 & 17.00 & 8.00 & 0.05 & 10.00 & 0.10 & 14.00 & 3.2 \\ \hline \end{array} \newline \ \newline \begin{array}{l|cccccr} \hline i & & & p_{ij} & & & \\ \hline 1 & 0.1312 & 0.1696 & 0.5569 & 0.0124 & 0.8283 & 0.5886 \\ 2 & 0.2329 & 0.4135 & 0.8307 & 0.3736 & 0.1004 & 0.9991 \\ 3 & 0.2348 & 0.1451 & 0.3522 & 0.2883 & 0.3047 & 0.6650 \\ 4 & 0.4047 & 0.8828 & 0.8732 & 0.5743 & 0.1091 & 0.0381 \\ \hline \end{array}$

with $x_i \in [0, 1]$ for $i = 1, ..., 6$ .

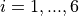Global optimum: 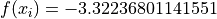$f(x_i) = -3.32236801141551$ for ${x} = [0.20168952, 0.15001069, 0.47687398, 0.27533243, 0.31165162, 0.65730054]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

class HelicalValley(dimensions=3)¶

HelicalValley objective function.

This class defines the HelicalValley global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{HelicalValley}}({x}) = 100{[z-10\Psi(x_1,x_2)]^2 +(\sqrt{x_1^2+x_2^2}-1)^2}+x_3^2$

Where, in this exercise:

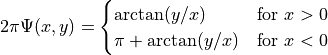
$2\pi\Psi(x,y) = \begin{cases} \arctan(y/x) & \textrm{for } x > 0 \\ \pi + \arctan(y/x) & \textrm{for } x < 0 \end{cases}$

with $x_i \in [-100, 100]$ for $i = 1, 2, 3$ .

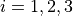Global optimum: $f(x) = 0$ for $x = [1, 0, 0]$

Fletcher, R. & Powell, M. A Rapidly Convergent Descent Method for Minimzation, Computer Journal, 1963, 62, 163-168

Todo

Jamil equation is different to original reference. The above paper can be obtained from http://galton.uchicago.edu/~lekheng/courses/302/classics/fletcher-powell.pdf

class HimmelBlau(dimensions=2)¶

HimmelBlau objective function.

This class defines the HimmelBlau global optimization problem. This is a multimodal minimization problem defined as follows:

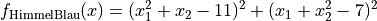
$f_{\text{HimmelBlau}}({x}) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2 - 7)^2$

with $x_i \in [-6, 6]$ for $i = 1, 2$ .

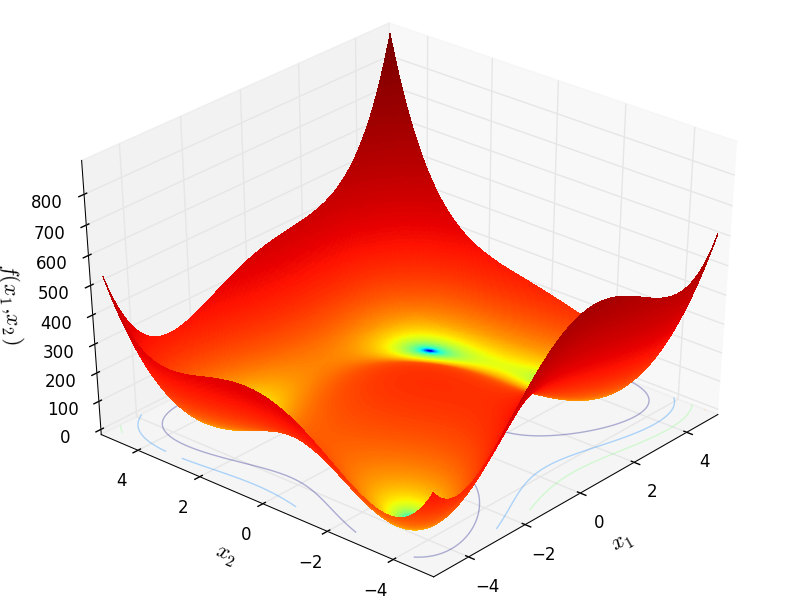
Two-dimensional HimmelBlau function

Global optimum: $f(x) = 0$ for $x = [3, 2]$

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

class HolderTable01(dimensions=2)¶

HolderTable objective function.

This class defines the HolderTable global optimization problem. This is a multimodal minimization problem defined as follows:

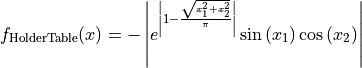
$f_{\text{HolderTable}}({x}) = - \left|{e^{\left|{1 - \frac{\sqrt{x_{1}^{2} + x_{2}^{2}}}{\pi} }\right|} \sin\left(x_{1}\right) \cos\left(x_{2}\right)}\right|$

with $x_i \in [-10, 10]$ for $i = 1, 2$ .

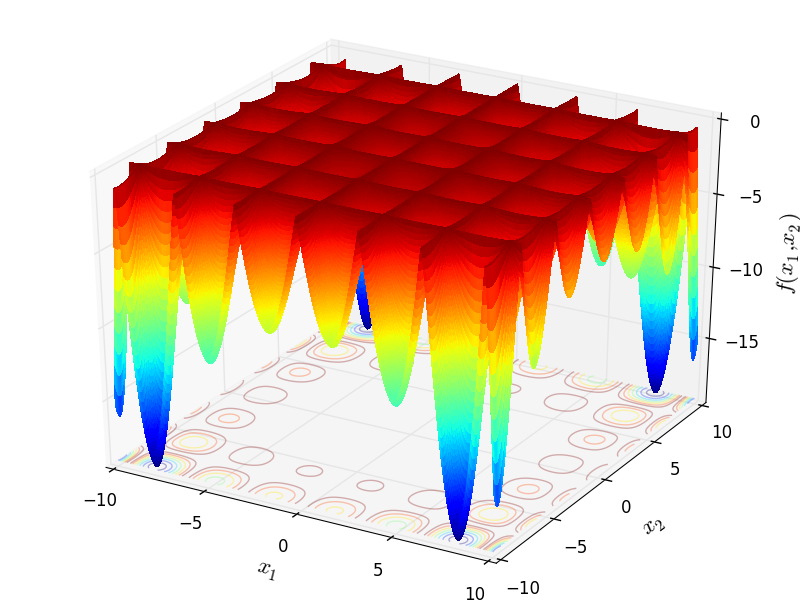
Two-dimensional HolderTable01 function

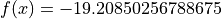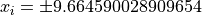Global optimum: $f(x) = -19.20850256788675$ for $x_i = \pm 9.664590028909654$ for $i = 1, 2$

Gavana, A. Global Optimization Benchmarks and AMPGO

Todo

Jamil #146 equation is wrong - should be squaring the x1 and x2 terms, but isn’t. Gavana does.

class HolderTable02(dimensions=2)¶: HolderTable objective function.

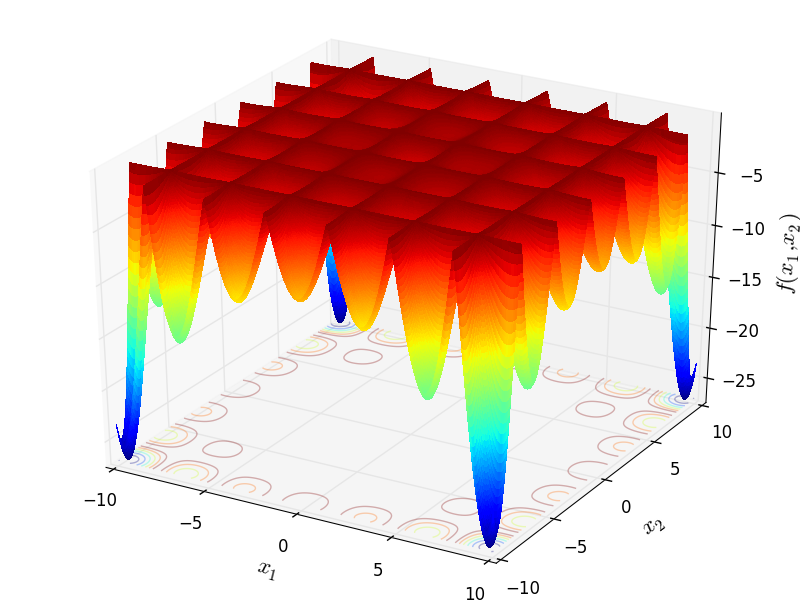
Two-dimensional HolderTable02 function

class Hosaki(dimensions=2)¶

Hosaki objective function.

This class defines the Hosaki global optimization problem. This is a multimodal minimization problem defined as follows:

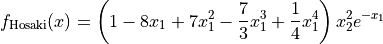
$f_{\text{Hosaki}}(x) = \left ( 1 - 8 x_1 + 7 x_1^2 - \frac{7}{3} x_1^3 + \frac{1}{4} x_1^4 \right ) x_2^2 e^{-x_1}$

with $x_i \in [0, 10]$ for $i = 1, 2$ .

Two-dimensional Hosaki function

Global optimum: 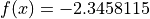$f(x) = -2.3458115$ for $x = [4, 2]$ .

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.

class Hougen(dimensions=5)¶: Hougen objective function.

class HyperGrid(dimensions=2)¶: HyperGrid objective function.

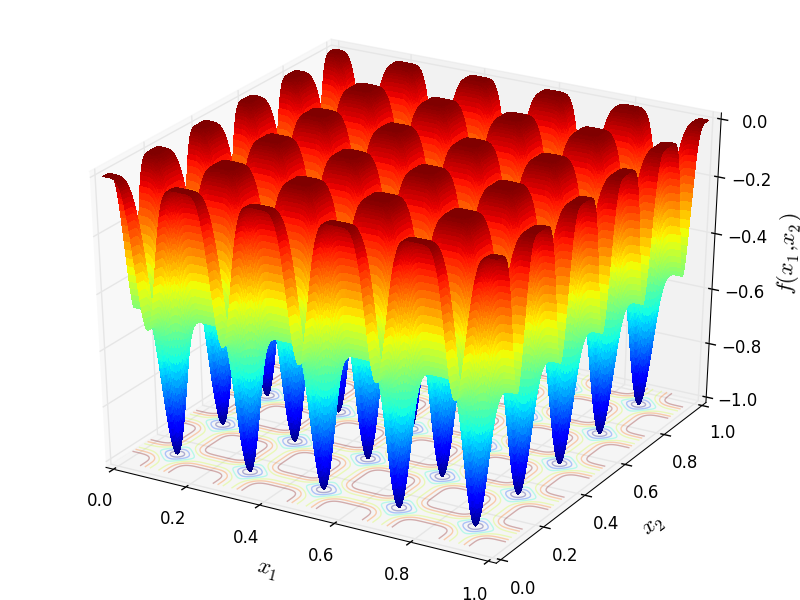
Two-dimensional HyperGrid function

N-D Test Functions H¶

Previous topic

Next topic

This Page

Navigation

N-D Test Functions H¶

Previous topic

Next topic

This Page

Quick search

Navigation