Navigation
- index
- next |
- previous |
- Home »
- SciPy Test Functions Index »
- N-D Test Functions P
 N-D Test Functions P¶
N-D Test Functions P¶Parsopoulos objective function.
This class defines the Parsopoulos global optimization problem. This is a multimodal minimization problem defined as follows:
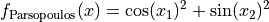
with ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
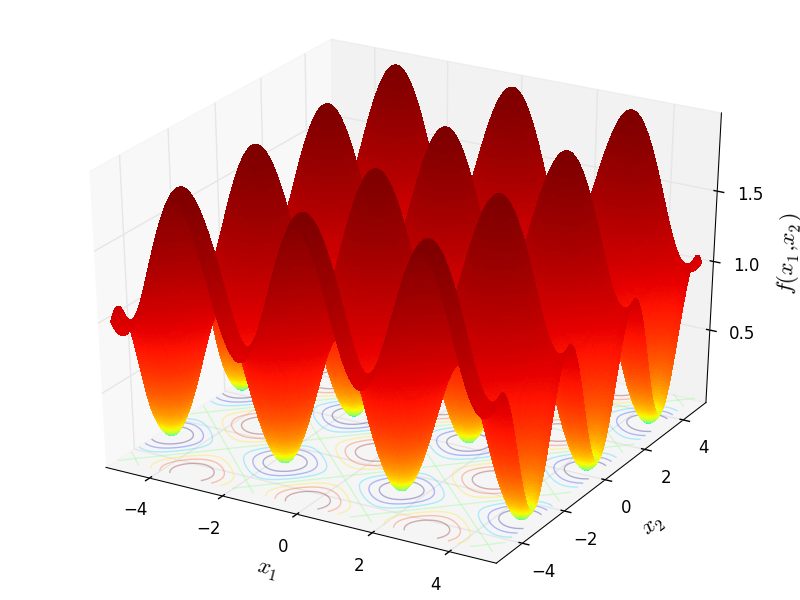
Two-dimensional Parsopoulos function
Global optimum: This function has infinite number of global minima in R2,
at points 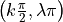 ,
where
,
where 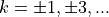 and
and 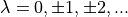
In the given domain problem, function has 12 global minima all equal to zero.
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Pathological objective function.
This class defines the Pathological global optimization problem. This is a multimodal minimization problem defined as follows:
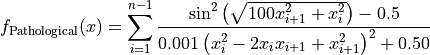
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
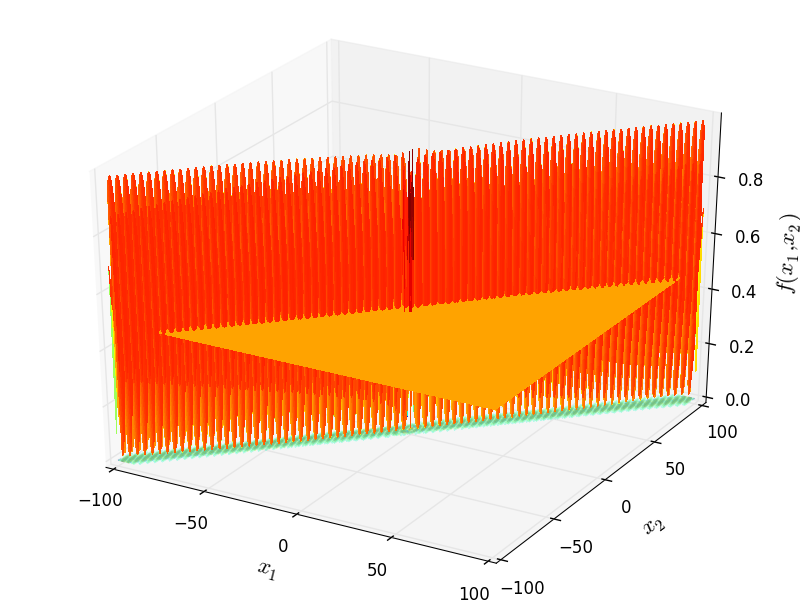
Two-dimensional Pathological function
Global optimum: 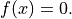 for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png) for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Paviani objective function.
This class defines the Paviani global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Paviani}}(x) = \sum_{i=1}^{10} \left[\log^{2}\left(10
- x_i\right) + \log^{2}\left(x_i -2\right)\right]
- \left(\prod_{i=1}^{10} x_i^{10} \right)^{0.2}](_images/math/3435d59819638f197d92ed62cceaf2c34bb07556.png)
with ![x_i \in [2.001, 9.999]](_images/math/636468723f60098daa93400984ff0cd953b9408c.png) for
for 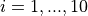 .
.
Global optimum: 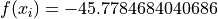 for
for
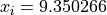 for
for 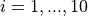
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Todo
think Gavana web/code definition is wrong because final product term shouldn’t raise x to power 10.
Peaks objective function.
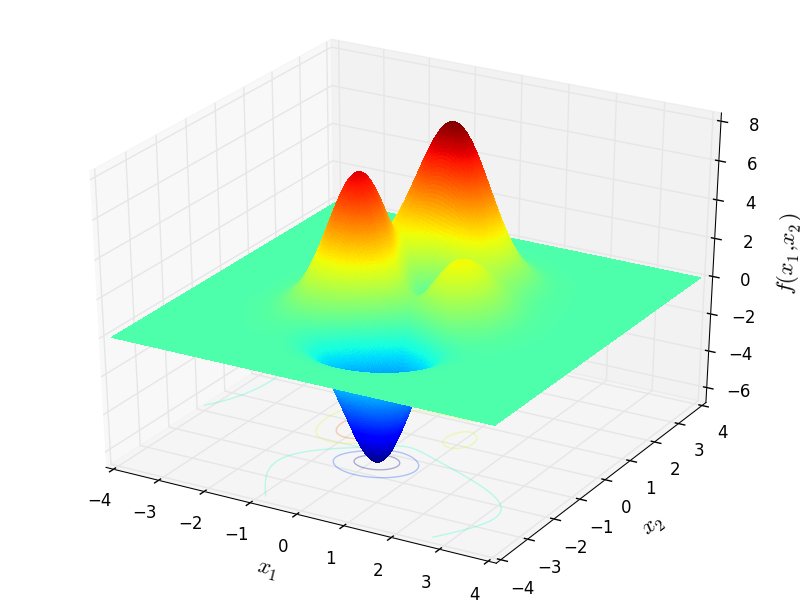
Two-dimensional Peaks function
Penalty 1 objective function.
This class defines the Penalty 1 global optimization problem. This is a imultimodal minimization problem defined as follows:
![f_{\text{Penalty01}}(x) = \frac{\pi}{30} \left\{10 \sin^2(\pi y_1)
+ \sum_{i=1}^{n-1} (y_i - 1)^2 \left[1 + 10 \sin^2(\pi y_{i+1}) \right]
+ (y_n - 1)^2 \right \} + \sum_{i=1}^n u(x_i, 10, 100, 4)](_images/math/6f889a24623e95a25aa6f040cbfbbeadde49aa60.png)
Where, in this exercise:
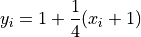
And:
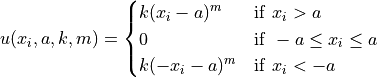
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for 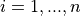 .
.
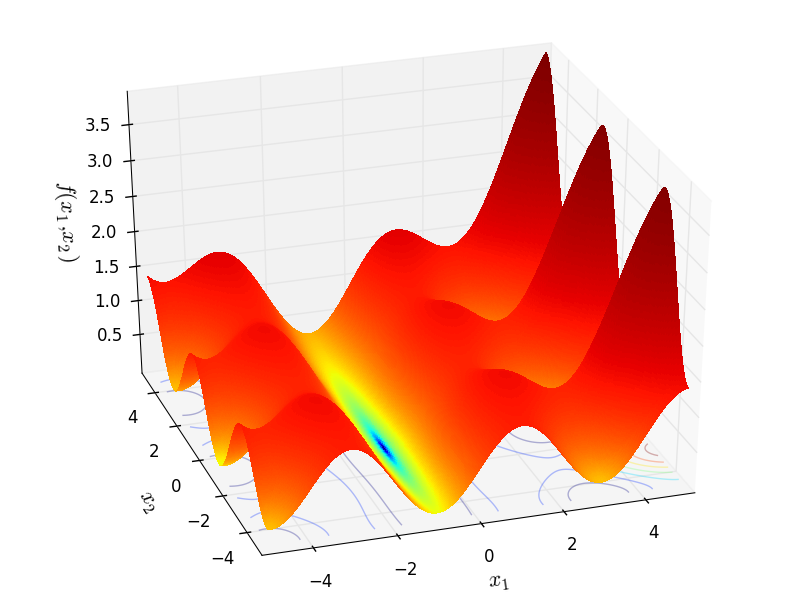
Two-dimensional Penalty01 function
Global optimum:  for
for 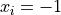 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Penalty 2 objective function.
This class defines the Penalty 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Penalty02}}(x) = 0.1 \left\{\sin^2(3\pi x_1) + \sum_{i=1}^{n-1}
(x_i - 1)^2 \left[1 + \sin^2(3\pi x_{i+1}) \right ]
+ (x_n - 1)^2 \left [1 + \sin^2(2 \pi x_n) \right ]\right \}
+ \sum_{i=1}^n u(x_i, 5, 100, 4)](_images/math/3141f3002097e158b708eb19464dd20871320191.png)
Where, in this exercise:
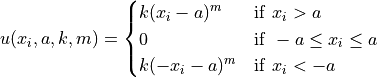
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
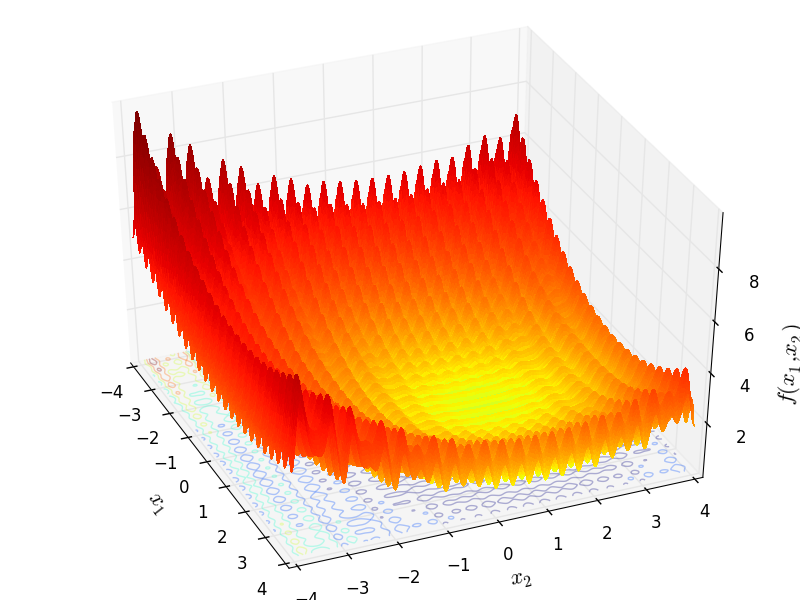
Two-dimensional Penalty02 function
Global optimum:  for
for 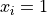 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
PenHolder objective function.
This class defines the PenHolder global optimization problem. This is a multimodal minimization problem defined as follows:
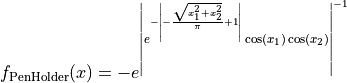
with ![x_i \in [-11, 11]](_images/math/64a0f2c8fc7fe30ca047d2d61f93c549fc261011.png) for
for  .
.
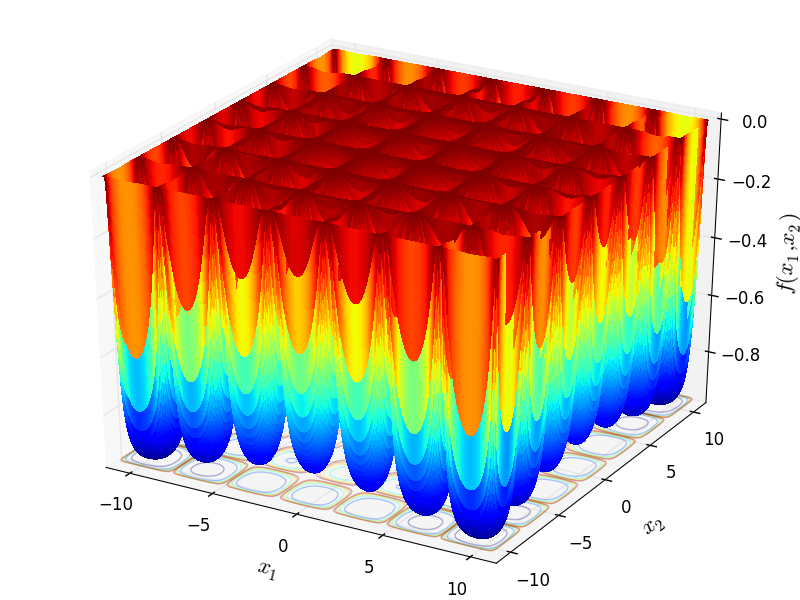
Two-dimensional PenHolder function
Global optimum: 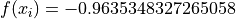 for
for
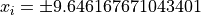 for
for 
Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
PermFunction 1 objective function.
This class defines the PermFunction1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PermFunction01}}(x) = \sum_{k=1}^n \left\{ \sum_{j=1}^n (j^k
+ \beta) \left[ \left(\frac{x_j}{j}\right)^k - 1 \right] \right\}^2](_images/math/312bf0e32bb73e897ad36e12a66a173fd7dabe9a.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-n, n + 1]](_images/math/c3bb9fec8c8e7fe2d1aea671920e928ef7a2aba8.png) for
for  .
.
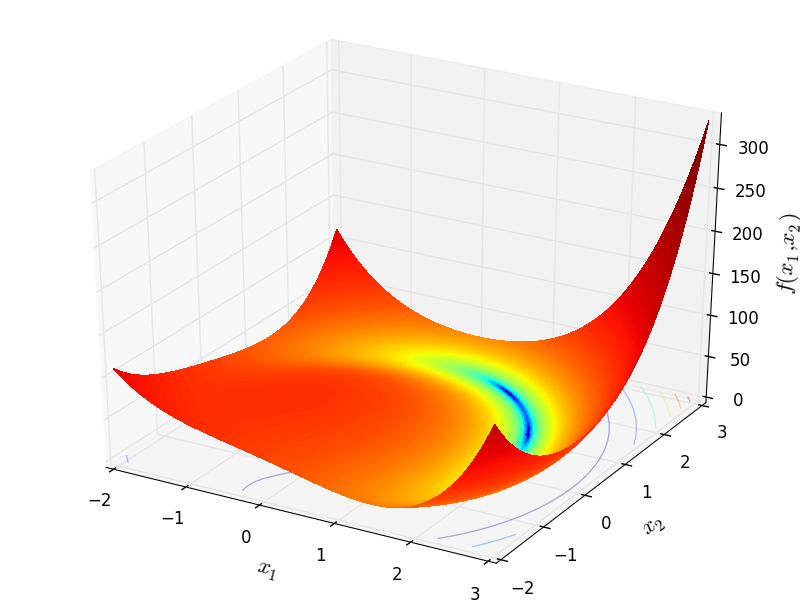
Two-dimensional PermFunction01 function
Global optimum:  for
for 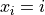 for
for

Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
line 560
PermFunction 2 objective function.
This class defines the Perm Function 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PermFunction02}}(x) = \sum_{k=1}^n \left\{ \sum_{j=1}^n (j
+ \beta) \left[ \left(x_j^k - {\frac{1}{j}}^{k} \right )
\right] \right\}^2](_images/math/29e920d5e9b5b270e16686693356017d43cd6927.png)
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-n, n+1]](_images/math/e90363f6e33a222e1f7df54a9864b6465e704e3e.png) for
for  .
.
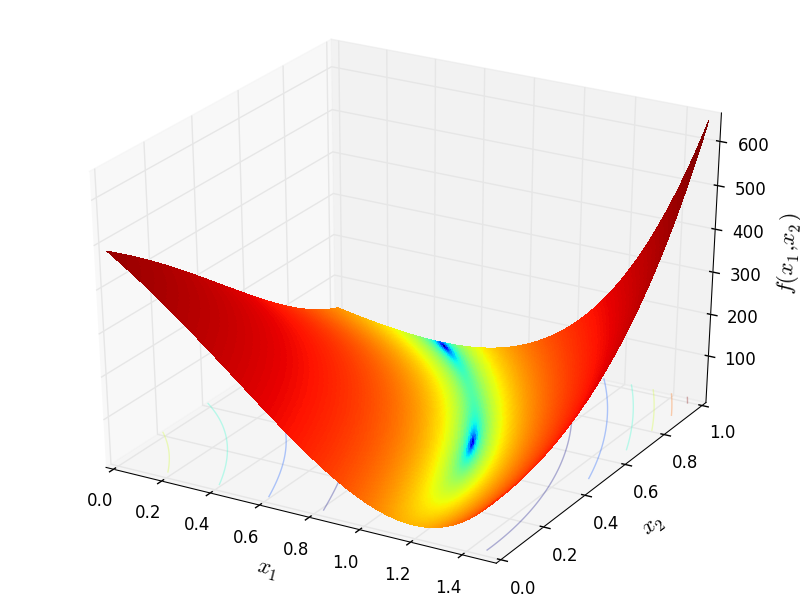
Two-dimensional PermFunction02 function
Global optimum:  for
for 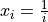 for
for 
Mishra, S. Global Optimization by Differential Evolution and Particle Swarm Methods: Evaluation on Some Benchmark Functions. Munich Personal RePEc Archive, 2006, 1005
Todo
line 582
Picheny objective function.
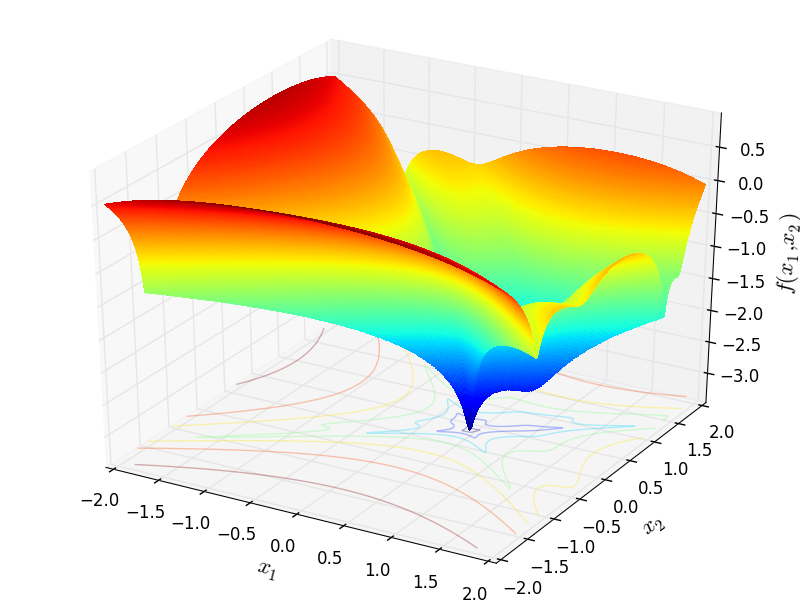
Two-dimensional Picheny function
Pinter objective function.
This class defines the Pinter global optimization problem. This is a multimodal minimization problem defined as follows:
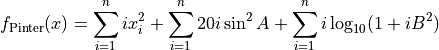
Where, in this exercise:
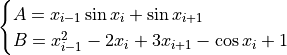
Where 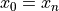 and
and 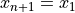 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
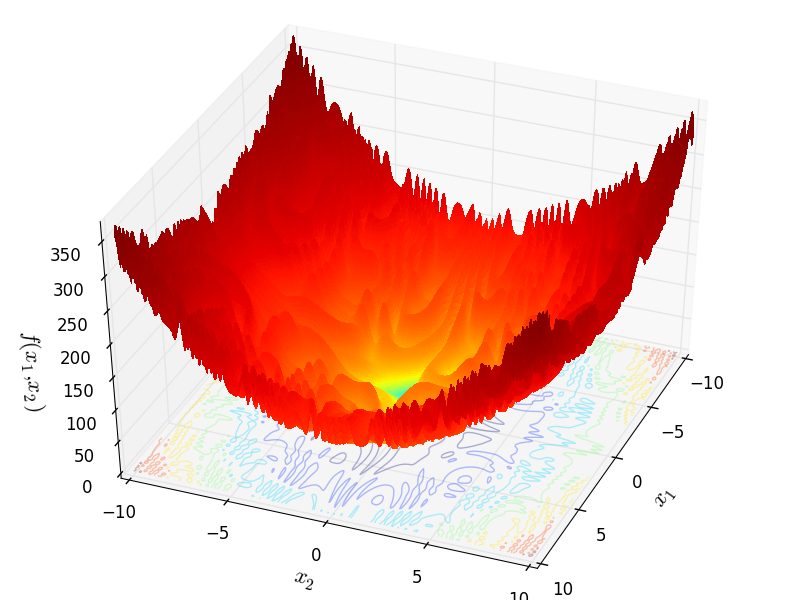
Two-dimensional Pinter function
Global optimum:  for
for 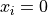 for
for

Jamil, M. & Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems Int. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4, 150-194.
Plateau objective function.
This class defines the Plateau global optimization problem. This is a multimodal minimization problem defined as follows:
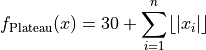
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.
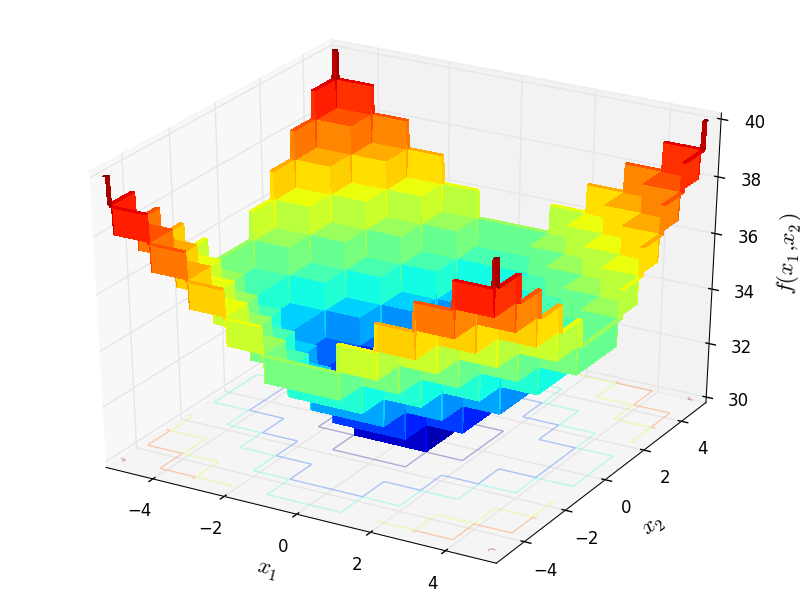
Two-dimensional Plateau function
Global optimum: 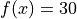 for
for 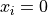 for
for

Gavana, A. Global Optimization Benchmarks and AMPGO
Powell objective function.
This class defines the Powell global optimization problem. This is a multimodal minimization problem defined as follows:
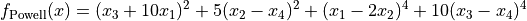
Here,  represents the number of dimensions and
represents the number of dimensions and
![x_i \in [-4, 5]](_images/math/a8851241896afaa6b5f64eff8d113a185f56a5ed.png) for
for 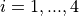 .
.
Global optimum:  for
for 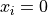 for
for
Powell, M. An iterative method for finding stationary values of a function of several variables Computer Journal, 1962, 5, 147-151
Power sum objective function.
This class defines the Power Sum global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PowerSum}}(x) = \sum_{k=1}^n\left[\left(\sum_{i=1}^n x_i^k
\right) - b_k \right]^2](_images/math/38ff58f47d79bd0f53de3635e264522ff184c65f.png)
Where, in this exercise, ![b = [8, 18, 44, 114]](_images/math/105fe65062105f09244d347b86485a3a8b9b8c4a.png)
Here, ![x_i \in [0, 4]](_images/math/e85f9417023b4ca79e827af77dce3a90c436cad5.png) for
for 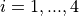 .
.
Global optimum:  for
for ![x = [1, 2, 2, 3]](_images/math/c49f0160f4173f54e320ca80677f9420e9d1aeec.png)
Gavana, A. Global Optimization Benchmarks and AMPGO
Price 1 objective function.
This class defines the Price 1 global optimization problem. This is a multimodal minimization problem defined as follows:
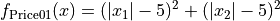
with ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
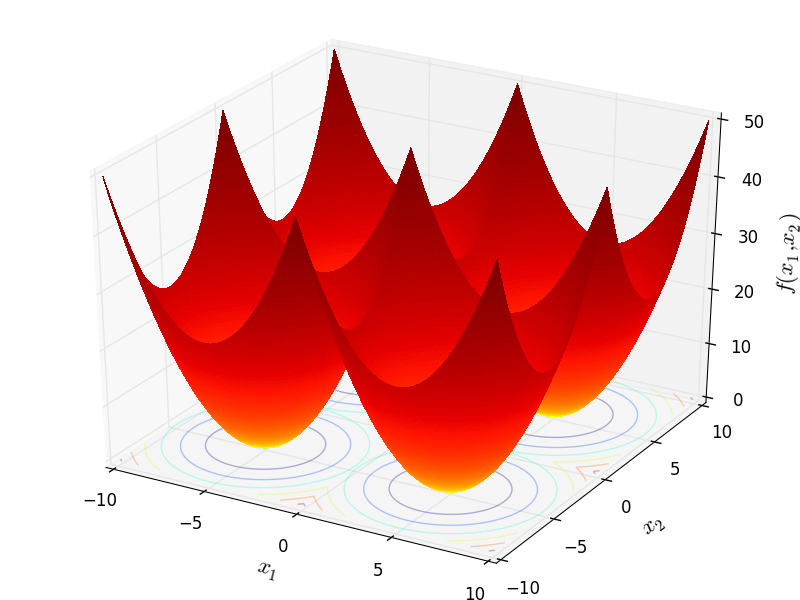
Two-dimensional Price01 function
Global optimum: 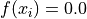 for
for ![x = [5, 5]](_images/math/d119ca22009801699ebcd310e20f782894560d02.png) or
or
![x = [5, -5]](_images/math/590e5a822acdac1d66677e7419f5f73405b6a7ad.png) or
or ![x = [-5, 5]](_images/math/c351c3b47b26a30a748656cedf78e2fa93f9abab.png) or
or ![x = [-5, -5]](_images/math/522ed9cd65e251175292500419f750604a07aa45.png) .
.
Price, W. A controlled random search procedure for global optimisation Computer Journal, 1977, 20, 367-370
Price 2 objective function.
This class defines the Price 2 global optimization problem. This is a multimodal minimization problem defined as follows:
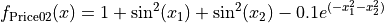
with ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
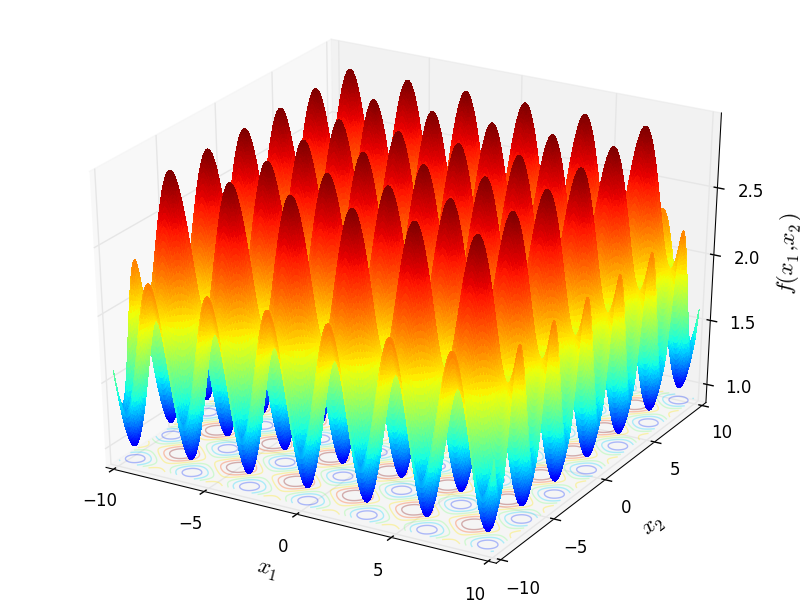
Two-dimensional Price02 function
Global optimum: 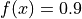 for
for ![x_i = [0, 0]](_images/math/38a8058deb8aa25845466f1492ef4f7853a28d5f.png)
Price, W. A controlled random search procedure for global optimisation Computer Journal, 1977, 20, 367-370
Price 3 objective function.
This class defines the Price 3 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Price03}}(x) = 100(x_2 - x_1^2)^2 + \left[6.4(x_2 - 0.5)^2
- x_1 - 0.6 \right]^2](_images/math/82a7e986362bb5e244dc695c14ea20cd3f1bb4fa.png)
with ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
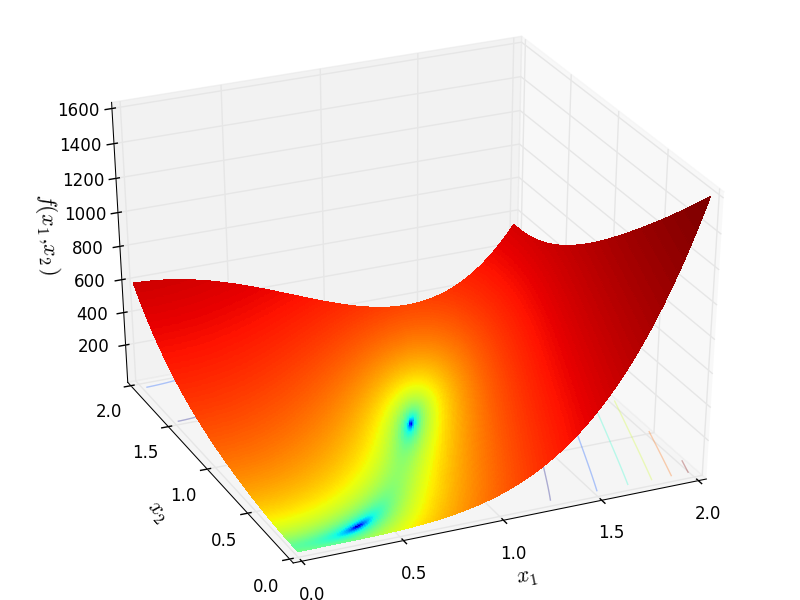
Two-dimensional Price03 function
Global optimum:  for
for ![x = [-5, -5]](_images/math/522ed9cd65e251175292500419f750604a07aa45.png) ,
,
![x = [-5, 5]](_images/math/c351c3b47b26a30a748656cedf78e2fa93f9abab.png) ,
, ![x = [5, -5]](_images/math/590e5a822acdac1d66677e7419f5f73405b6a7ad.png) ,
, ![x = [5, 5]](_images/math/d119ca22009801699ebcd310e20f782894560d02.png) .
.
Price, W. A controlled random search procedure for global optimisation Computer Journal, 1977, 20, 367-370
Todo
Jamil #96 has an erroneous factor of 6 in front of the square brackets
Price 4 objective function.
This class defines the Price 4 global optimization problem. This is a multimodal minimization problem defined as follows:
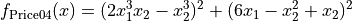
with ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
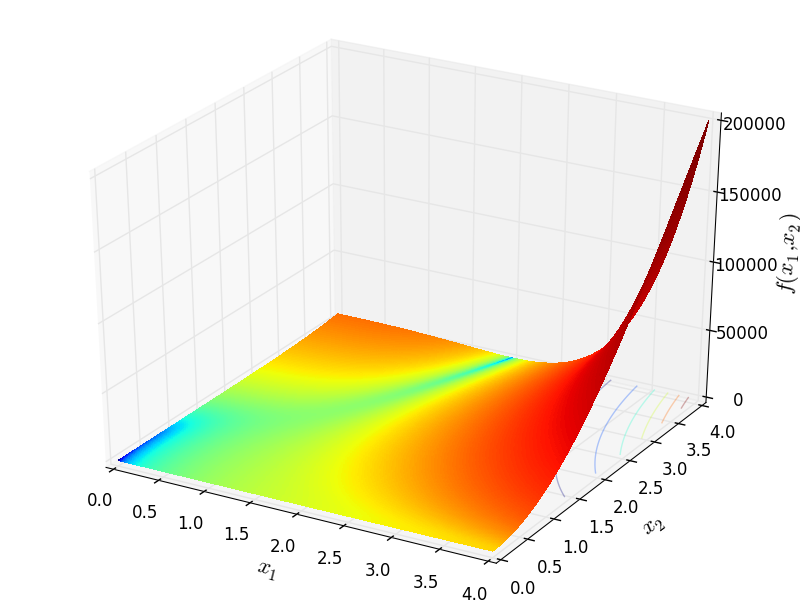
Two-dimensional Price04 function
Global optimum:  for
for ![x = [0, 0]](_images/math/45f5b5de4a67315f59227449efaecb2b749a4db5.png) ,
,
![x = [2, 4]](_images/math/6596346816820573eab7a89255dee3306e6deae4.png) and
and ![x = [1.464, -2.506]](_images/math/541aaf3d284971176943e2415da6d89dc96ce34c.png)
Price, W. A controlled random search procedure for global optimisation Computer Journal, 1977, 20, 367-370