Navigation
- index
- next |
- previous |
- Home »
- The Benchmarks »
- RandomFields
 RandomFields¶
RandomFields¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| No | No | Hard |
The approach used in the RandomFields test suite is described in https://www.researchgate.net/publication/301940420_Global_optimization_test_problems_based_on_random_field_composition . It generates benchmark functions by “smoothing” one or more multidimensional discrete random fields and composing them, and it is composed by three different steps:
No source code is given, but the implementation is fairly straightforward from the article itself.
 Methodology¶
Methodology¶For the Multidimensional Discrete Random Field (MDRF) generator, the generator function (referred to as operator 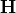 ),
takes a multidimensional vector
),
takes a multidimensional vector 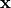 of floating point values from the unit hypercube domain as an input, and maps it to a value from a given
set
of floating point values from the unit hypercube domain as an input, and maps it to a value from a given
set 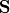 with a discrete probability distribution and a computational type (e.g. binary integer or float) of
choice:
with a discrete probability distribution and a computational type (e.g. binary integer or float) of
choice:
![y = H(x_1, x_2, x_d, ..., x_n) \: \: \textup{where} \: \: x_d \in [0, 1] \: \: \textup{for} \: \: d=1, 2, ..., n \: \: \textup{and} \: \: y \in \mathbf{S}](_images/math/b675d77e678f70a6af787da0b5e274af7a8de42e.png)
To explain the concept of the implementation, a related discretized version of this idea can be defined as:
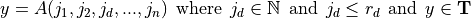
Operator 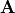 can be interpreted as high-dimensional random “array” A with indices
can be interpreted as high-dimensional random “array” A with indices 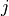 of which each index
of which each index
 is bounded by the maximum array size
is bounded by the maximum array size  for dimension
for dimension 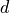 . In the second expression,
. In the second expression, 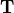 is a finite set of successive
integers pointing to the distinct elements of the set
is a finite set of successive
integers pointing to the distinct elements of the set 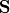 .
.
The concept chosen for the MDRF generator algorithm is to compute and reproduce the pseudo-random values of the high-dimensional arrays “on the fly” instead of storing a potentially huge passive map in the computer memory. Another alternative interpretation would be to consider operator :math:A as a pseudorandom number generator with a high-dimensional vector as its generating seed.
Using a multiplicative weighting function as expressed in equation below these discrete random fields can be transformed to “smooth” differentiable continuous random fields:
![\mathbf{C} (\mathbf{x}, \mathbf{r}, \boldsymbol{\varphi}, p) =\left [ \prod_{d=1}^{n} (1 - e^{cos(2\pi(r_d(x_d+\varphi_d)))-1})(\frac{1}{1-e^{-2}}) \right ]^p](_images/math/f99f241dfd2daa4606ca4f11c9f6361234b734a3.png)
Where 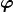 denotes the vector of the (phase) shift of the discrete field and the
denotes the vector of the (phase) shift of the discrete field and the  operator such that also
fields with non-zero values along the domain boundaries can be constructed (
operator such that also
fields with non-zero values along the domain boundaries can be constructed (![\varphi_d \in [0,1]](_images/math/43111afc5e1267e4beead70cca93f1dc558eee03.png) ). With parameter
). With parameter 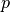 the shape of the function can be adjusted.
the shape of the function can be adjusted.
The application of the “bare bones” discrete random fields generated by the algorithm above is of little practical interest because of the primitive problem structure. Compositions of such fields of different and heterogeneous resolutions, dimensions and codomain distributions can provide test functions with interesting problem structures. Continuous fields with different spatial resolution can be created, and compositions can be made by for example multiplication or by weighted addition such as for example:
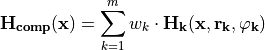
where 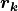 and
and 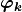 (both in bold) denote the vectors with the array size and shifts for each dimension of
composition fields
(both in bold) denote the vectors with the array size and shifts for each dimension of
composition fields  .
.
To cut the story short, my approach in generating the test functions for the RandomFields benchmarks hs been:
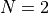 and
and 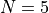
 can be 0.25, 0.5, 1, 2, or 3
can be 0.25, 0.5, 1, 2, or 3In this way, I have generated 120 test functions for each dimension, for a total of 480 benchmarks.
One of the main differences between the RandomFields benchmark and most of the other test suites is that neither the global optimum position nor the actual minimum value of the objective function is known. So, in order to evaluate the solvers performances in a similar way as done previously, I have elected to follow this approach, for each of the 480 functions in the RandomFields test suite:
A few examples of 2D benchmark functions created with the RandomFields generator can be seen in Figure 10.1.
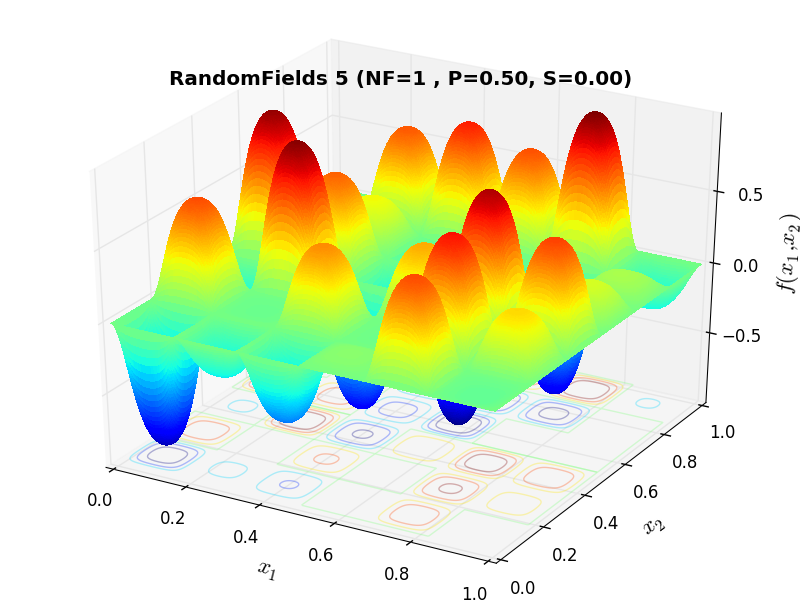
RandomFields Function 5 |
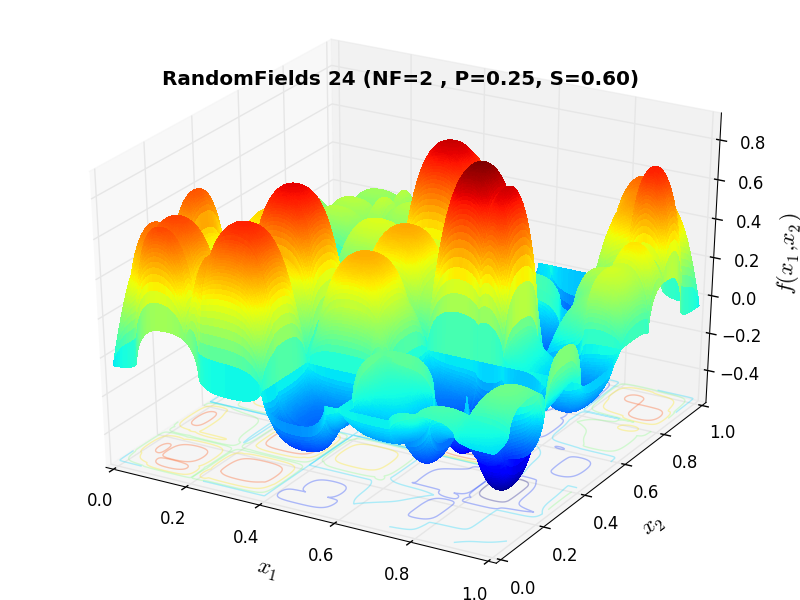
RandomFields Function 24 |
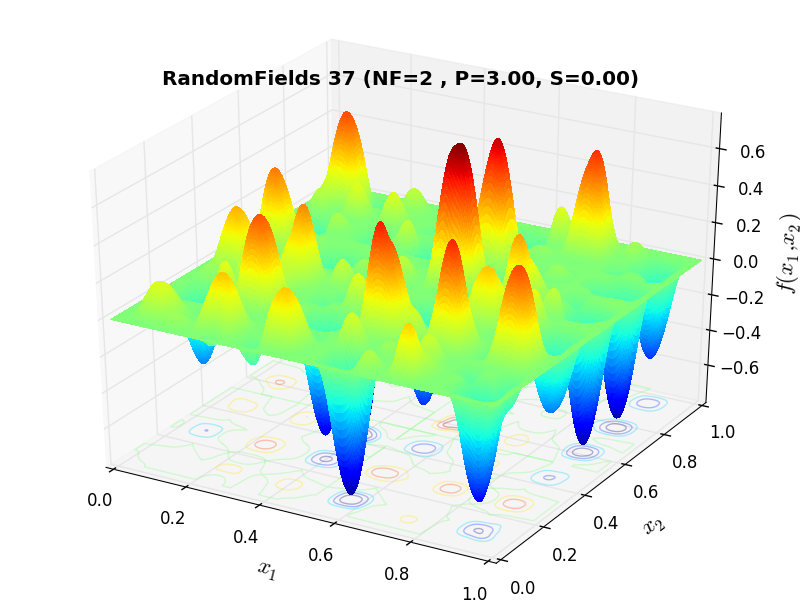
RandomFields Function 37 |
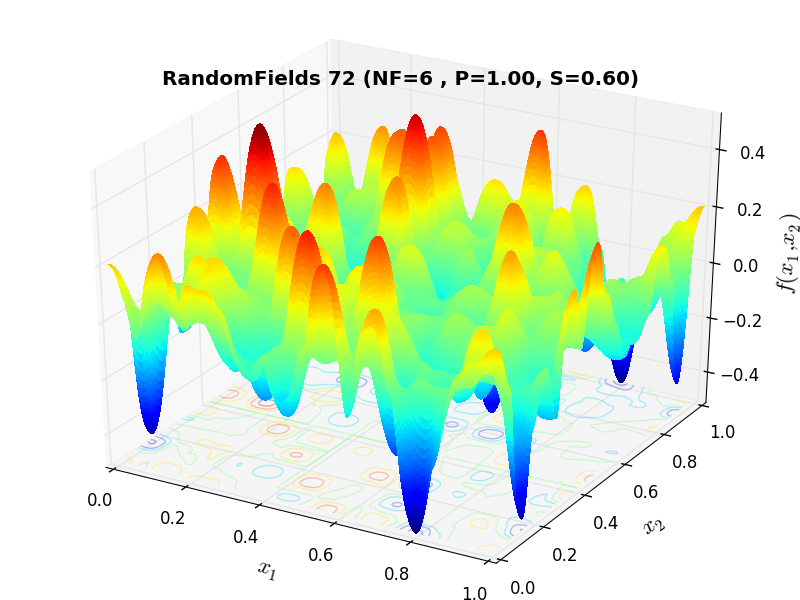
RandomFields Function 72 |
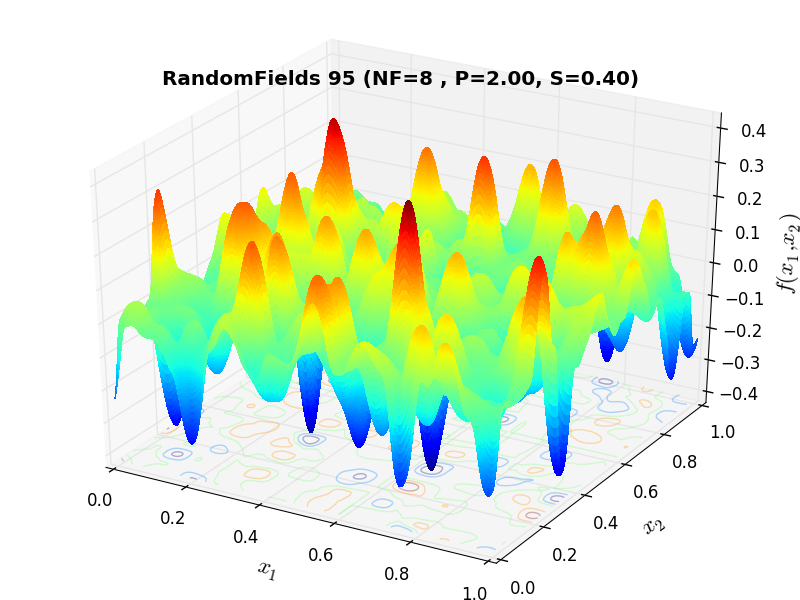
RandomFields Function 95 |
RandomFields Function 120 |
 General Solvers Performances¶
General Solvers Performances¶Table 10.1 below shows the overall success of all Global Optimization algorithms, considering every benchmark function,
for a maximum allowable budget of  .
.
The RandomFields benchmark suite is a relatively hard test suite: the best solver for  is DIRECT, with a success
rate of 34.4%, but DualAnnealing and SHGO achive pretty much the same results, closely followed by MCS.
is DIRECT, with a success
rate of 34.4%, but DualAnnealing and SHGO achive pretty much the same results, closely followed by MCS.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 10.62% | 880 |
| BasinHopping | 19.38% | 678 |
| BiteOpt | 24.79% | 598 |
| CMA-ES | 9.17% | 978 |
| CRS2 | 13.12% | 691 |
| DE | 19.79% | 1,091 |
| DIRECT | 34.38% | 435 |
| DualAnnealing | 34.17% | 510 |
| LeapFrog | 8.33% | 193 |
| MCS | 29.38% | 614 |
| PSWARM | 14.37% | 1,648 |
| SCE | 17.08% | 786 |
| SHGO | 33.96% | 513 |
These results are also depicted in Figure 10.2, which shows that DIRECT, DualAnnealing and SHGO are the better-performing optimization algorithms, followed by MCS.
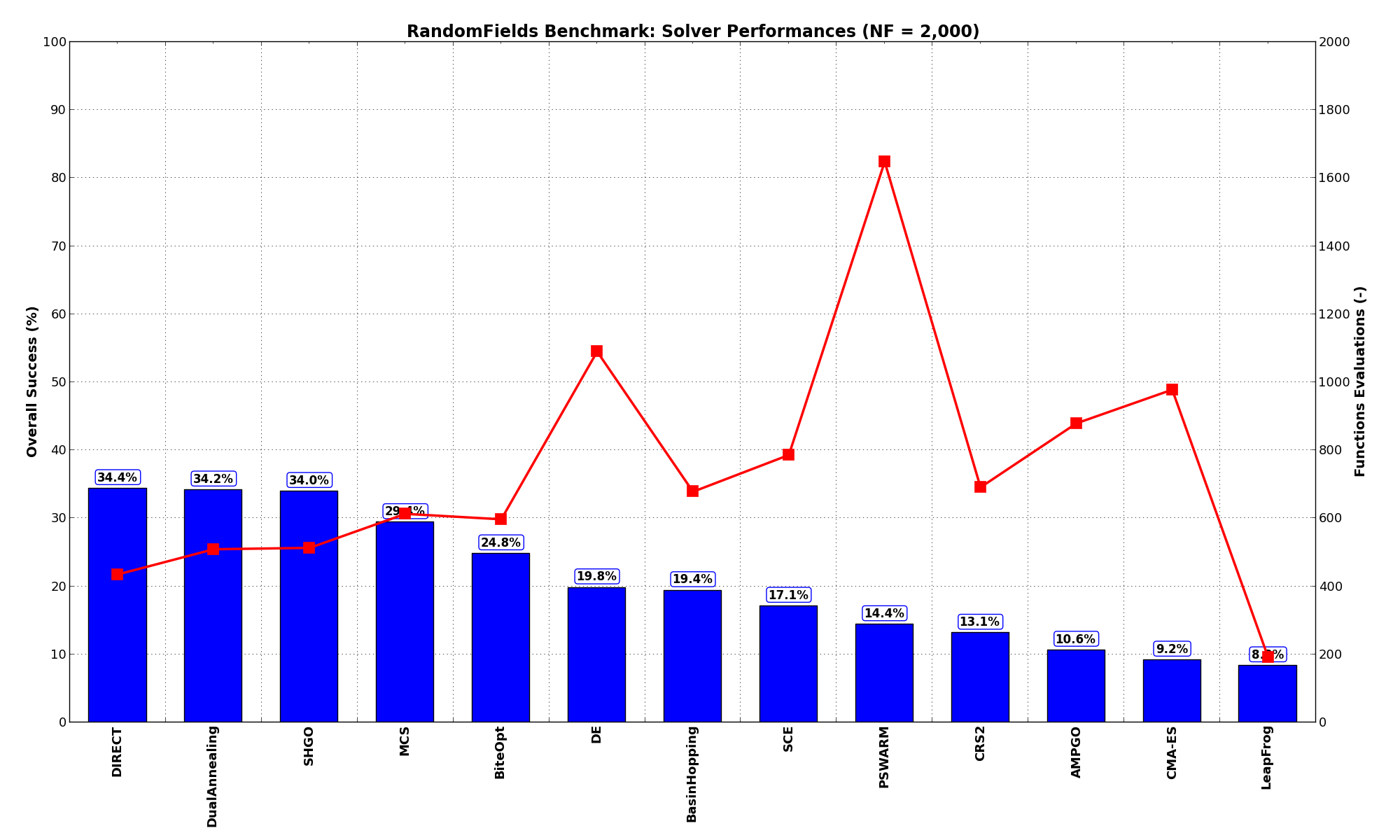
Figure 10.2: Optimization algorithms performances on the RandomFields test suite at 
Pushing the available budget to a very generous  , the results show SHGO taking the lead,
with MCS following by a large margin. The results are also shown visually in Figure 10.3.
, the results show SHGO taking the lead,
with MCS following by a large margin. The results are also shown visually in Figure 10.3.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 59.17% | 2,319 |
| BasinHopping | 88.33% | 1,312 |
| BiteOpt | 38.96% | 956 |
| CMA-ES | 52.29% | 1,665 |
| CRS2 | 37.08% | 1,032 |
| DE | 47.08% | 1,820 |
| DIRECT | 68.75% | 962 |
| DualAnnealing | 57.29% | 791 |
| LeapFrog | 23.75% | 270 |
| MCS | 87.08% | 1,614 |
| PSWARM | 47.08% | 2,110 |
| SCE | 43.12% | 806 |
| SHGO | 80.00% | 1,206 |
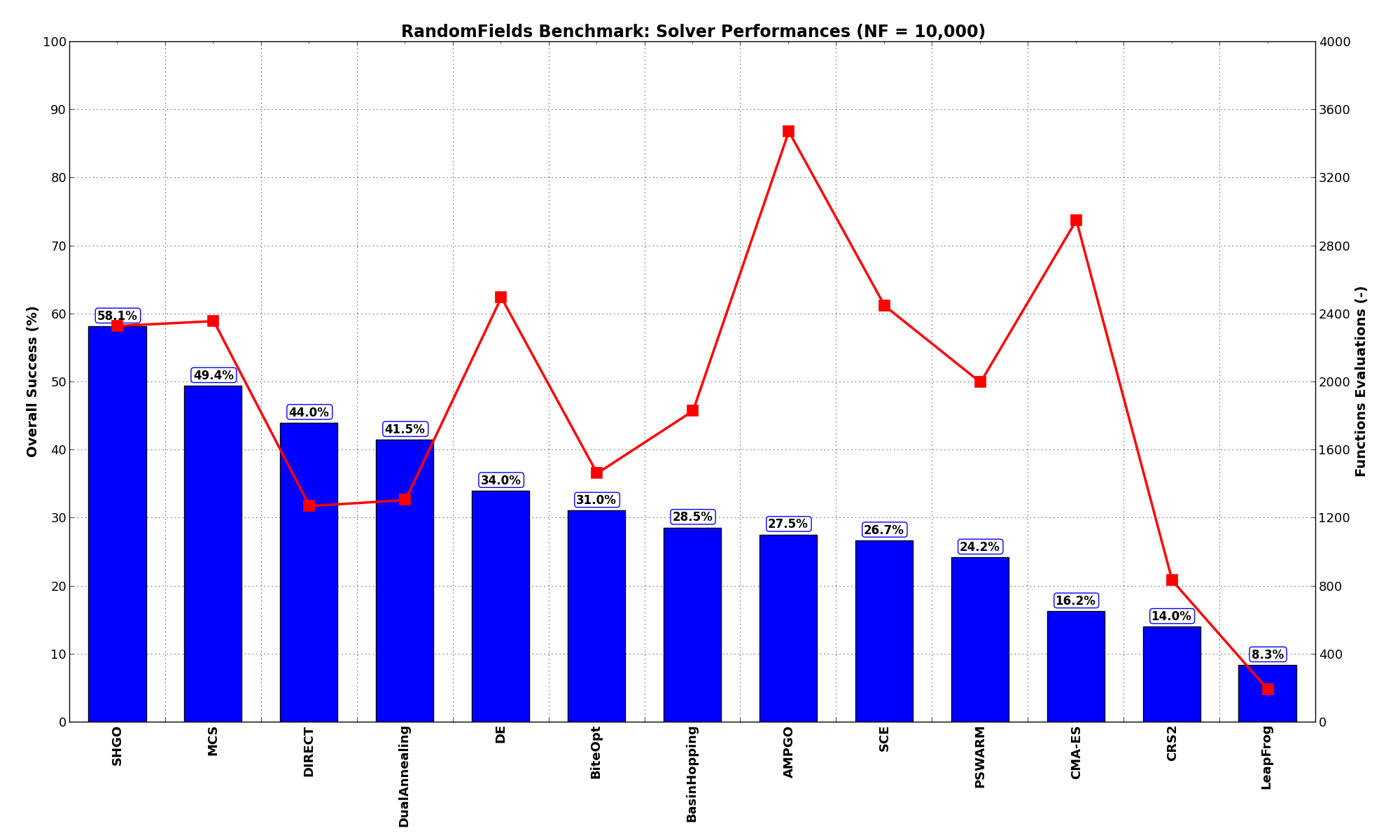
Figure 10.3: Optimization algorithms performances on the RandomFields test suite at 
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 10.4.
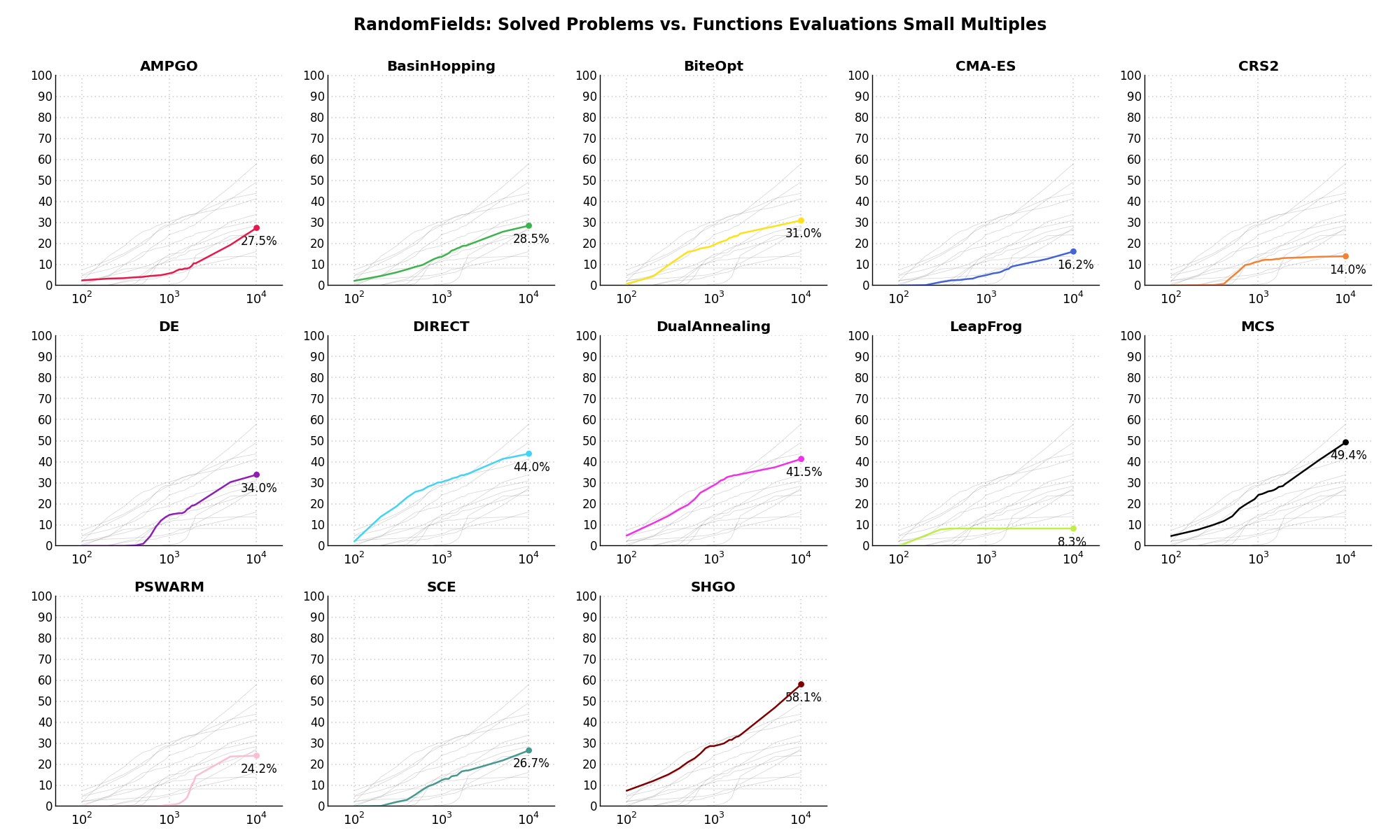
Figure 10.4: Percentage of problems solved given a fixed number of function evaluations on the RandomFields test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 10.5 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
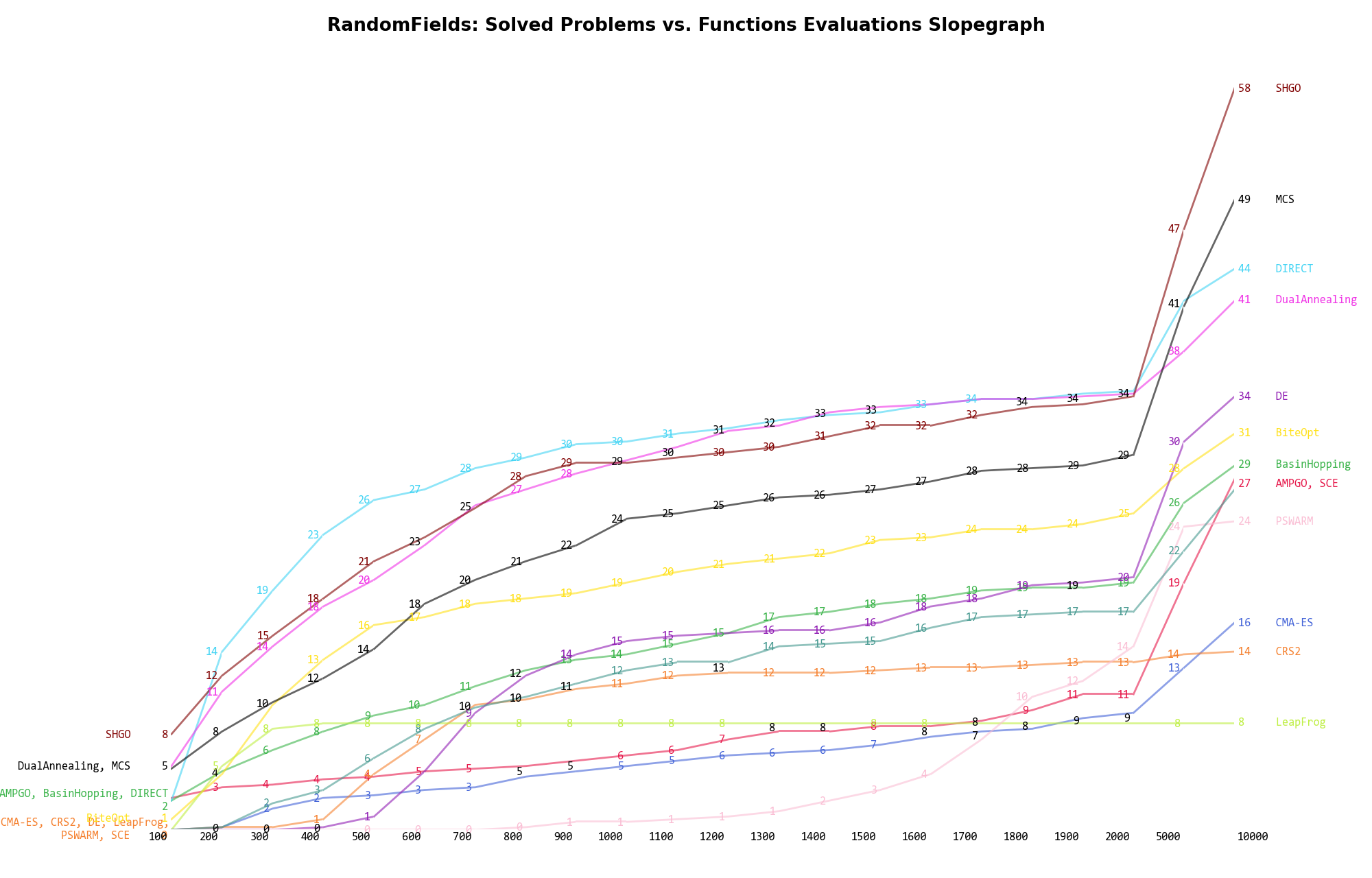
Figure 10.5: Percentage of problems solved given a fixed number of function evaluations on the RandomFields test suite
A few obvious conclusions we can draw from these pictures are:
 Dimensionality Effects¶
Dimensionality Effects¶Since I used the RandomFields test suite to generate test functions with dimensionality ranging from 2 to 5, it is interesting to take a look at the solvers performances as a function of the problem dimensionality. Of course, in general it is to be expected that for larger dimensions less problems are going to be solved - although it is not always necessarily so as it also depends on the function being generated. Results are shown in Table 10.3 .
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 27.5 | 8.3 | 3.3 | 3.3 | 10.6 |
| BasinHopping | 60.0 | 11.7 | 1.7 | 4.2 | 19.4 |
| BiteOpt | 60.0 | 20.0 | 5.8 | 13.3 | 24.8 |
| CMA-ES | 28.3 | 6.7 | 0.8 | 0.8 | 9.2 |
| CRS2 | 40.0 | 7.5 | 2.5 | 2.5 | 13.1 |
| DE | 64.2 | 15.0 | 0.0 | 0.0 | 19.8 |
| DIRECT | 86.7 | 28.3 | 12.5 | 10.0 | 34.4 |
| DualAnnealing | 82.5 | 29.2 | 15.8 | 9.2 | 34.2 |
| LeapFrog | 21.7 | 6.7 | 1.7 | 3.3 | 8.3 |
| MCS | 83.3 | 17.5 | 11.7 | 5.0 | 29.4 |
| PSWARM | 51.7 | 1.7 | 0.8 | 3.3 | 14.4 |
| SCE | 63.3 | 4.2 | 0.8 | 0.0 | 17.1 |
| SHGO | 93.3 | 23.3 | 9.2 | 10.0 | 34.0 |
Figure 10.6 shows the same results in a visual way.
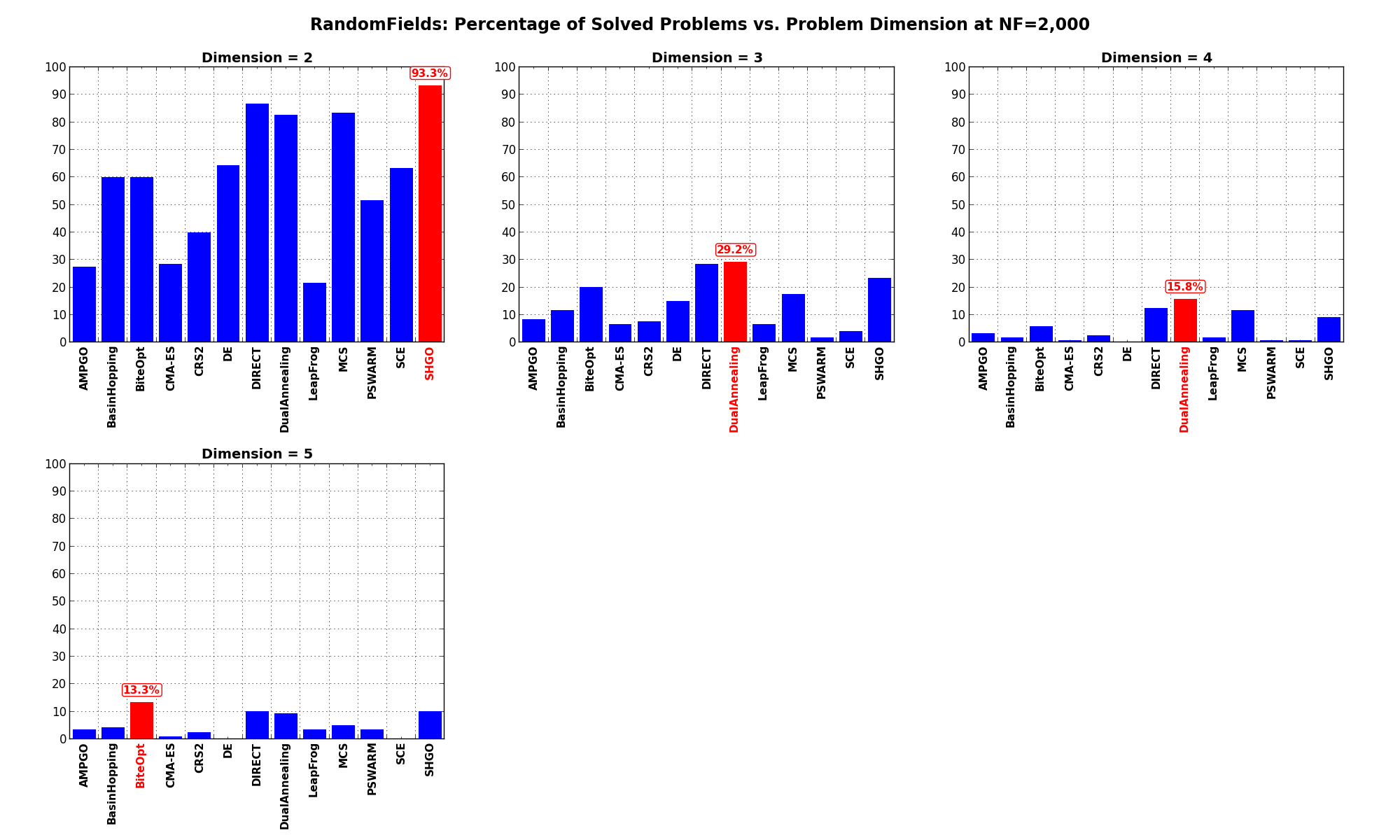
Figure 10.6: Percentage of problems solved as a function of problem dimension for the RandomFields test suite at 
What we can infer from the table and the figure is that, for low dimensionality problems (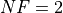 ), SHGO is able to solve
most of the problems in this test suite, with DIRECT and MCS tightly following. By increasing the dimensionality
the performances of all solvers degrade significantly, with DualAnnealing having a marginal advantage over other solvers.
), SHGO is able to solve
most of the problems in this test suite, with DIRECT and MCS tightly following. By increasing the dimensionality
the performances of all solvers degrade significantly, with DualAnnealing having a marginal advantage over other solvers.
Pushing the available budget to a very generous  shows SHGO solving all problems, with MCS and DIRECT right behind
for
shows SHGO solving all problems, with MCS and DIRECT right behind
for  . For higher dimensionalities, again performance degradation is evident, although SHGO is the clear winner.
. For higher dimensionalities, again performance degradation is evident, although SHGO is the clear winner.
The results for the benchmarks at  are displayed in Table 10.4 and Figure 10.7.
are displayed in Table 10.4 and Figure 10.7.
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 72.5 | 21.7 | 5.0 | 10.8 | 27.5 |
| BasinHopping | 73.3 | 24.2 | 6.7 | 10.0 | 28.5 |
| BiteOpt | 75.0 | 24.2 | 8.3 | 16.7 | 31.0 |
| CMA-ES | 43.3 | 11.7 | 5.8 | 4.2 | 16.2 |
| CRS2 | 40.0 | 8.3 | 4.2 | 3.3 | 14.0 |
| DE | 64.2 | 40.0 | 25.8 | 5.8 | 34.0 |
| DIRECT | 95.8 | 42.5 | 17.5 | 20.0 | 44.0 |
| DualAnnealing | 85.8 | 39.2 | 24.2 | 16.7 | 41.5 |
| LeapFrog | 21.7 | 6.7 | 1.7 | 3.3 | 8.3 |
| MCS | 98.3 | 58.3 | 25.0 | 15.8 | 49.4 |
| PSWARM | 66.7 | 17.5 | 6.7 | 5.8 | 24.2 |
| SCE | 76.7 | 22.5 | 6.7 | 0.8 | 26.7 |
| SHGO | 100.0 | 66.7 | 23.3 | 42.5 | 58.1 |
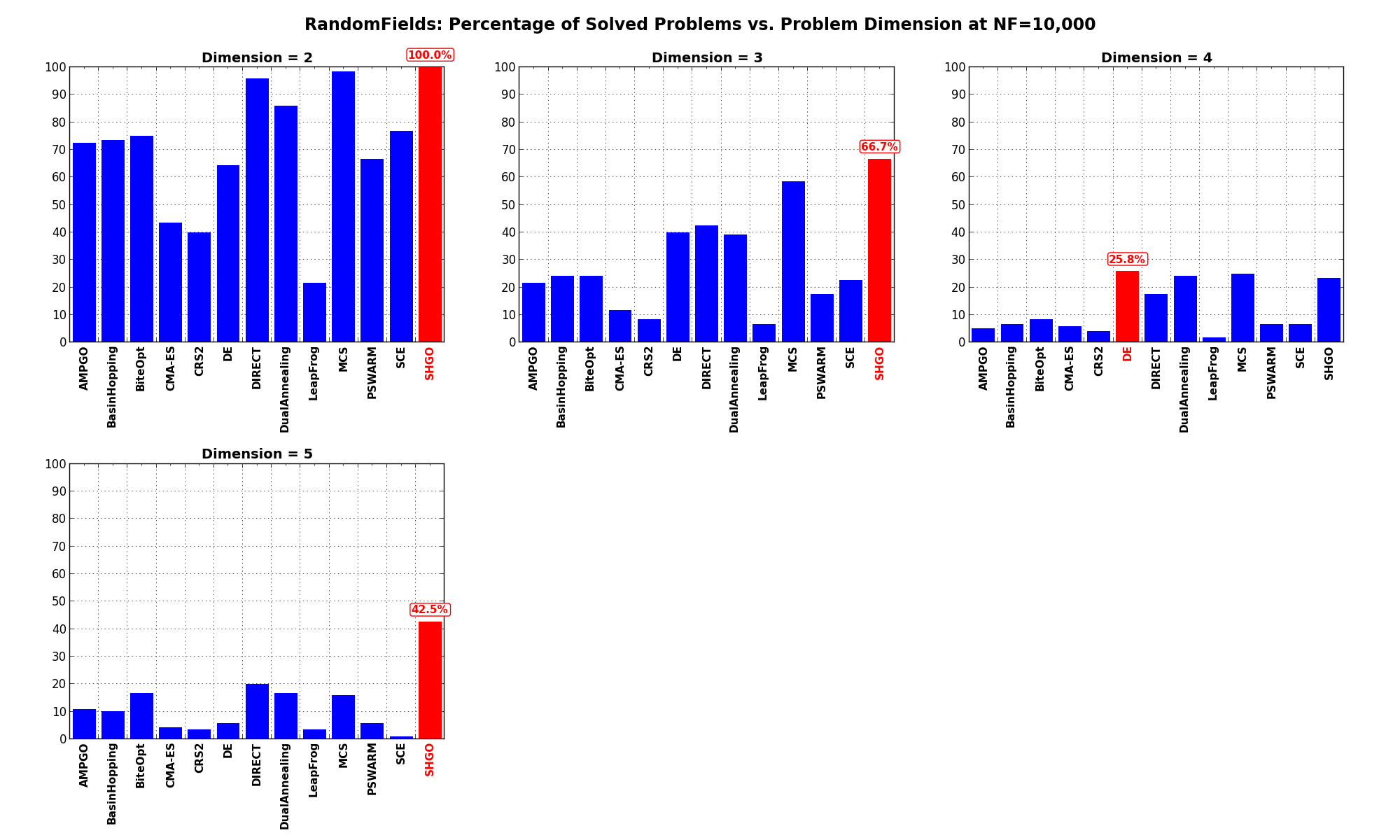
Figure 10.7: Percentage of problems solved as a function of problem dimension for the RandomFields test suite at 