Navigation
- index
- next |
- previous |
- Home »
- The Benchmarks »
- MPM2
 MPM2¶
MPM2¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| Yes | Yes | Medium |
Many test problems in real-valued optimization do not provide information about important problem properties, as, e. g., the positions of all local optima and the corresponding attraction basins. Knowing these characteristics would be helpful in many cases of benchmarking of optimization algorithms. Since many authors suggested to use parametrized problem generators that can produce test instances randomly but with controllable difficulty, several problem formulations appeared for which these new requirements can be handled well. The common ground of all these is that the objective function is generated by taking the maximum or minimum of several unimodal functions.
The implementation of this test function generator is described in detail in https://ls11-www.cs.tu-dortmund.de/_media/techreports/tr15-01.pdf .
 Methodology¶
Methodology¶The “Multiple Peaks Model 2” (MPM2) test suite produces multimodal problem instances by combining several randomly distributed peaks. Hence, the problems are irregular and non-separable, which are also important features of difficult real-world problems. The problem is defined by the following formulas:
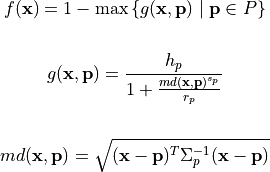
The objective function is given in the first equation. It takes the minimum of 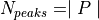 unimodal
functions (from the second equation) around peak positions
unimodal
functions (from the second equation) around peak positions 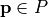 . This has the advantage that local optima
with known positions are created, which is necessary to calculate some quality indicators.
. This has the advantage that local optima
with known positions are created, which is necessary to calculate some quality indicators.
Each of these functions is associated with parameters 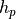 ,
, 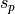 , and
, and 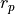 for height, shape,
and radius, respectively. By slightly deviating from locally quadratic behavior (
for height, shape,
and radius, respectively. By slightly deviating from locally quadratic behavior ( ), the test suite intends to
increase the difficulty for local search algorithms. Radii
), the test suite intends to
increase the difficulty for local search algorithms. Radii 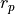 influence the size of attraction basins, and thus
the probability to place a starting point in the basin. Optima with small attraction basins will be difficult to find. Additionally, a randomly drawn covariance
matrix
influence the size of attraction basins, and thus
the probability to place a starting point in the basin. Optima with small attraction basins will be difficult to find. Additionally, a randomly drawn covariance
matrix 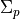 belongs to each peak. This matrix is used to create the optima’s basins as rotated hyperellipsoids, by calculating the Mahalanobis distance in
the third equation.
belongs to each peak. This matrix is used to create the optima’s basins as rotated hyperellipsoids, by calculating the Mahalanobis distance in
the third equation.
That said, my approach to generate test functions for this benchmark has been the following:
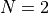 and
and 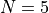
With all these variable settings, I generated 120 valid test function per dimension, thus the current MPM2 test suite contains 480 benchmark functions.
A few examples of 2D benchmark functions created with the MPM2 generator can be seen in Figure 9.1.
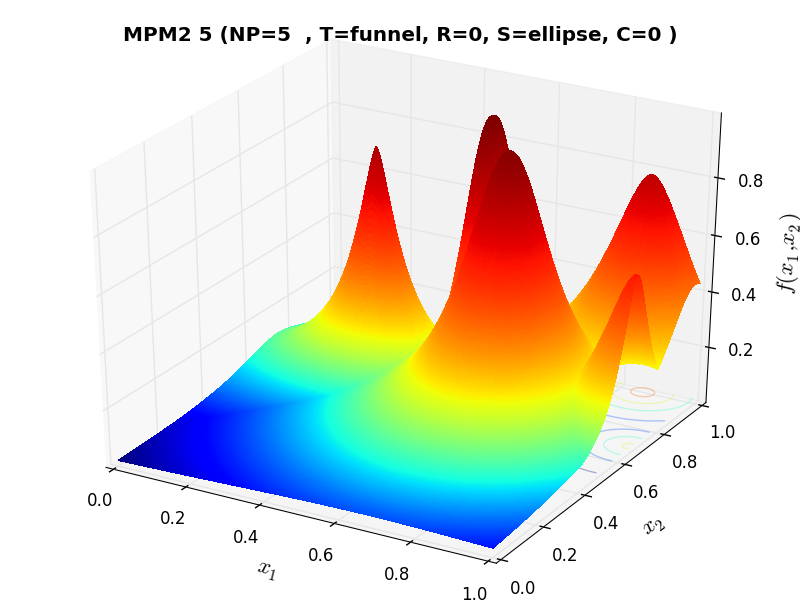
MPM2 Function 5 |
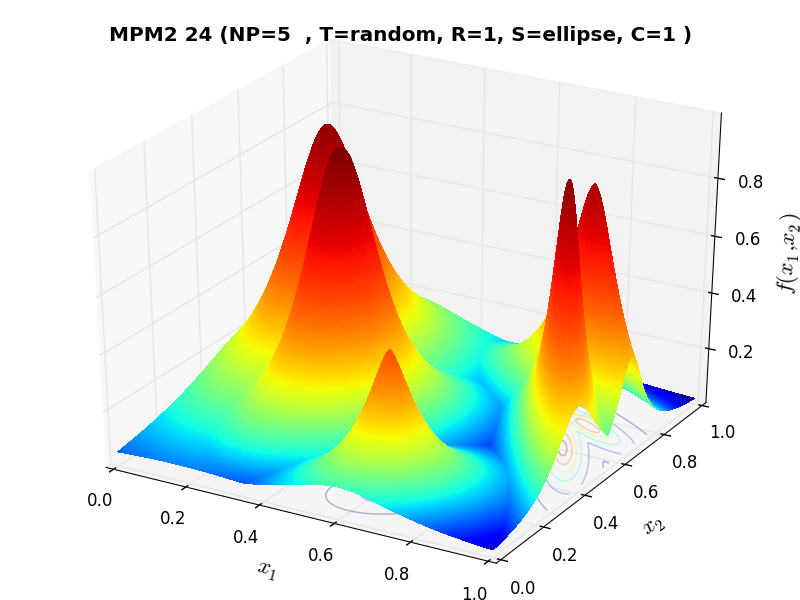
MPM2 Function 24 |
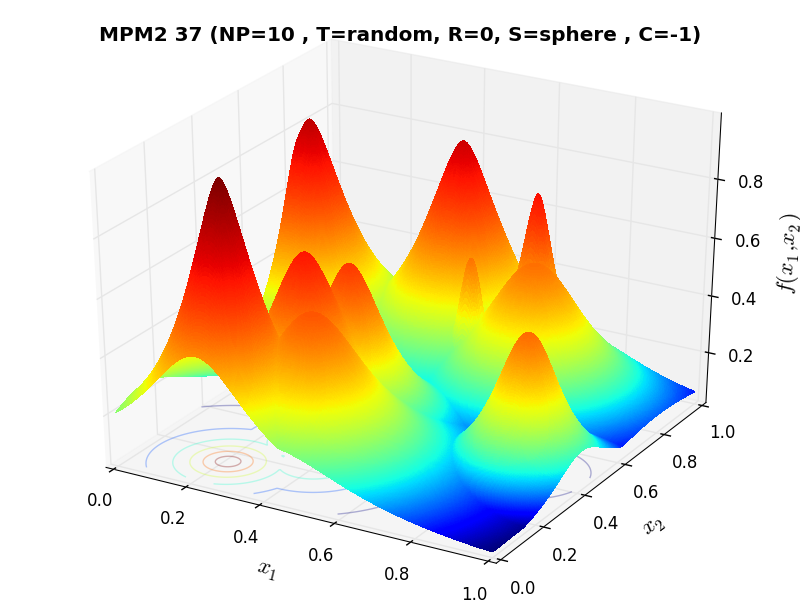
MPM2 Function 37 |
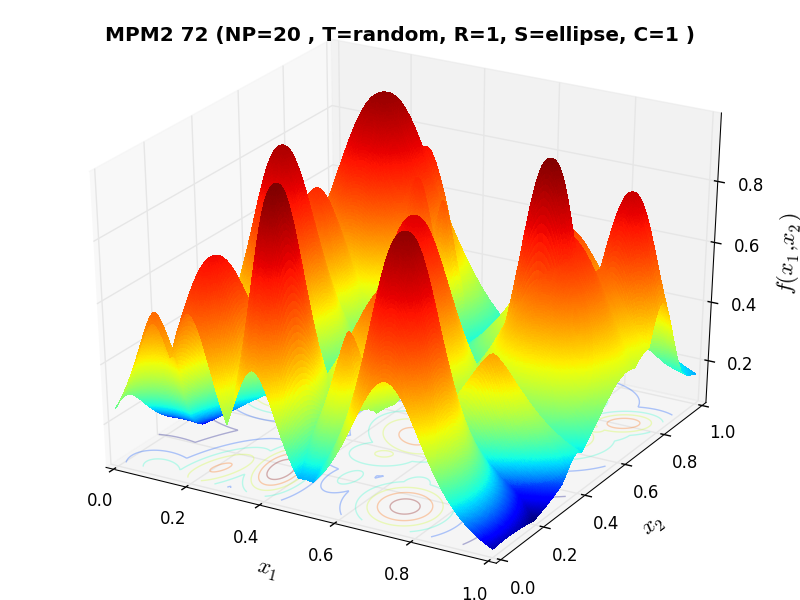
MPM2 Function 72 |
MPM2 Function 95 |
MPM2 Function 120 |
 General Solvers Performances¶
General Solvers Performances¶Table 9.1 below shows the overall success of all Global Optimization algorithms, considering every benchmark function,
for a maximum allowable budget of  .
.
The MPM2 benchmark suite is a relatively easy test suite: the best solver for  is BasinHopping, with a success
rate of 68.1%, closely followed by MCS and SHGO.
is BasinHopping, with a success
rate of 68.1%, closely followed by MCS and SHGO.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 36.04% | 660 |
| BasinHopping | 68.12% | 522 |
| BiteOpt | 35.00% | 462 |
| CMA-ES | 39.58% | 750 |
| CRS2 | 35.00% | 946 |
| DE | 32.92% | 1,170 |
| DIRECT | 59.79% | 464 |
| DualAnnealing | 50.62% | 376 |
| LeapFrog | 23.75% | 270 |
| MCS | 65.62% | 580 |
| PSWARM | 21.25% | 1,595 |
| SCE | 40.83% | 588 |
| SHGO | 65.21% | 510 |
These results are also depicted in Figure 9.2, which shows that BasinHopping is the better-performing optimization algorithm, followed by MCS and SHGO.
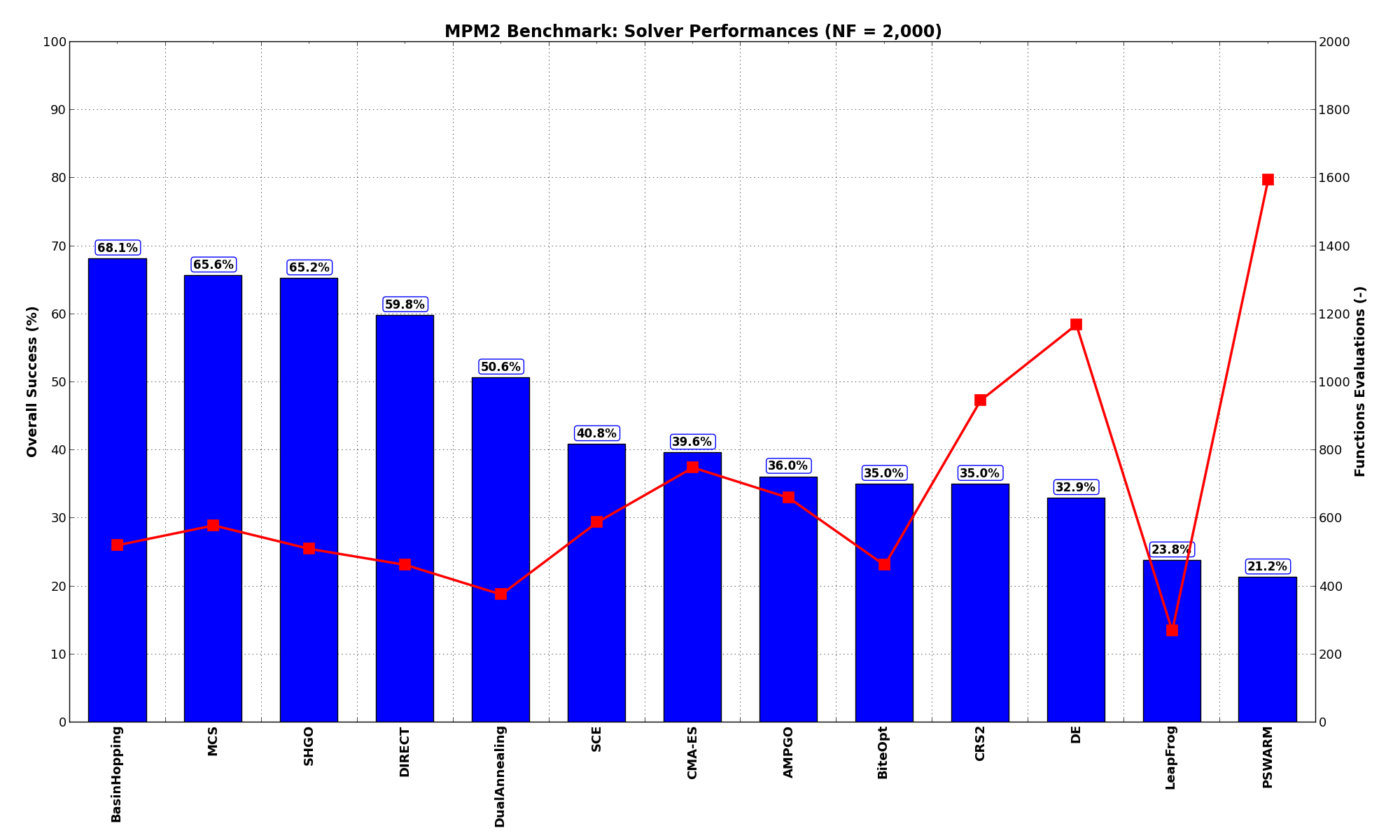
Figure 9.2: Optimization algorithms performances on the MPM2 test suite at 
Pushing the available budget to a very generous  , the results show BasinHopping still keeping the lead,
with MCS much closer now and SHGO trailing a bit behind. The results are also shown visually in Figure 9.3.
, the results show BasinHopping still keeping the lead,
with MCS much closer now and SHGO trailing a bit behind. The results are also shown visually in Figure 9.3.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 59.17% | 2,319 |
| BasinHopping | 88.33% | 1,312 |
| BiteOpt | 38.96% | 956 |
| CMA-ES | 52.29% | 1,665 |
| CRS2 | 37.08% | 1,032 |
| DE | 47.08% | 1,820 |
| DIRECT | 68.75% | 962 |
| DualAnnealing | 57.29% | 791 |
| LeapFrog | 23.75% | 270 |
| MCS | 87.08% | 1,614 |
| PSWARM | 47.08% | 2,110 |
| SCE | 43.12% | 806 |
| SHGO | 80.00% | 1,206 |
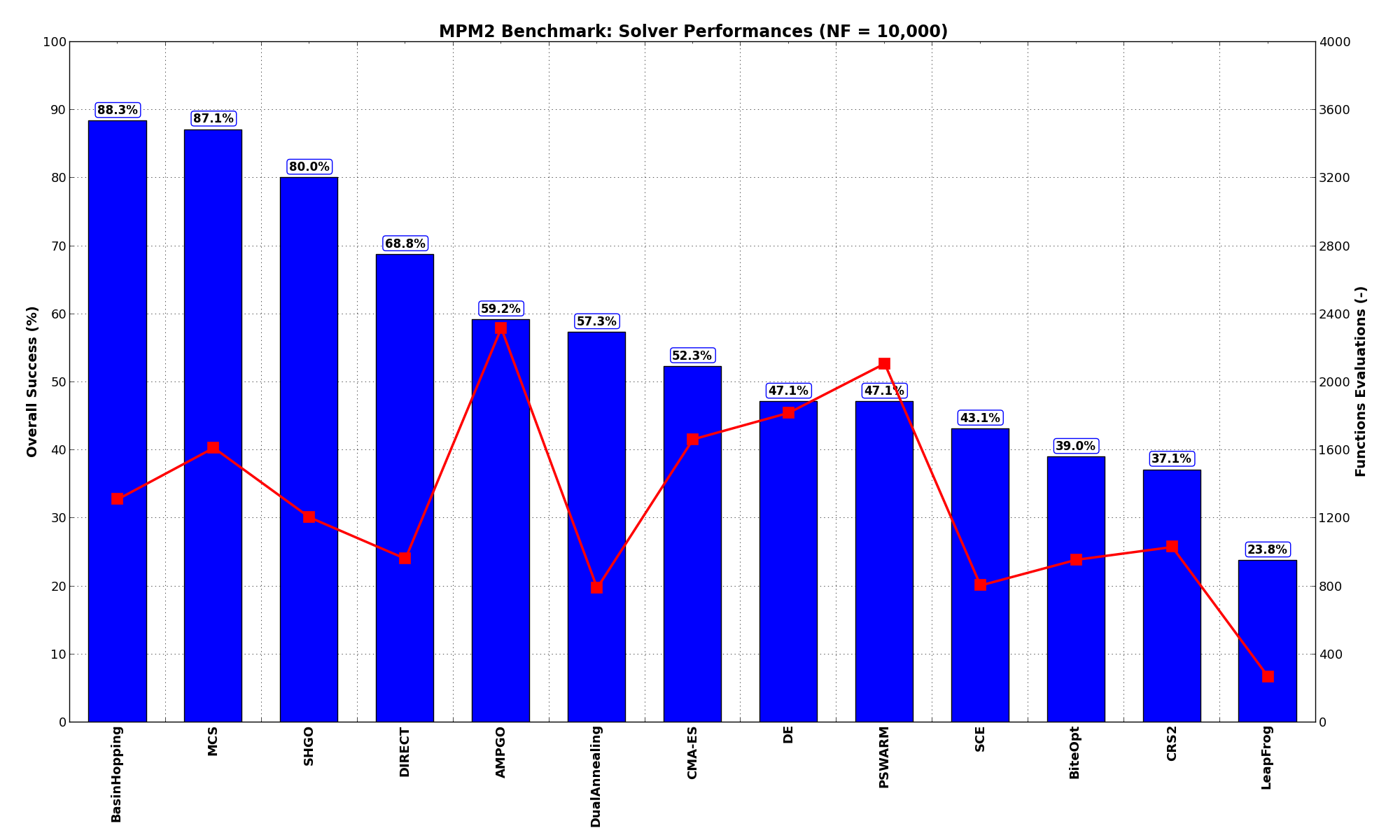
Figure 9.3: Optimization algorithms performances on the MPM2 test suite at 
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 9.4.
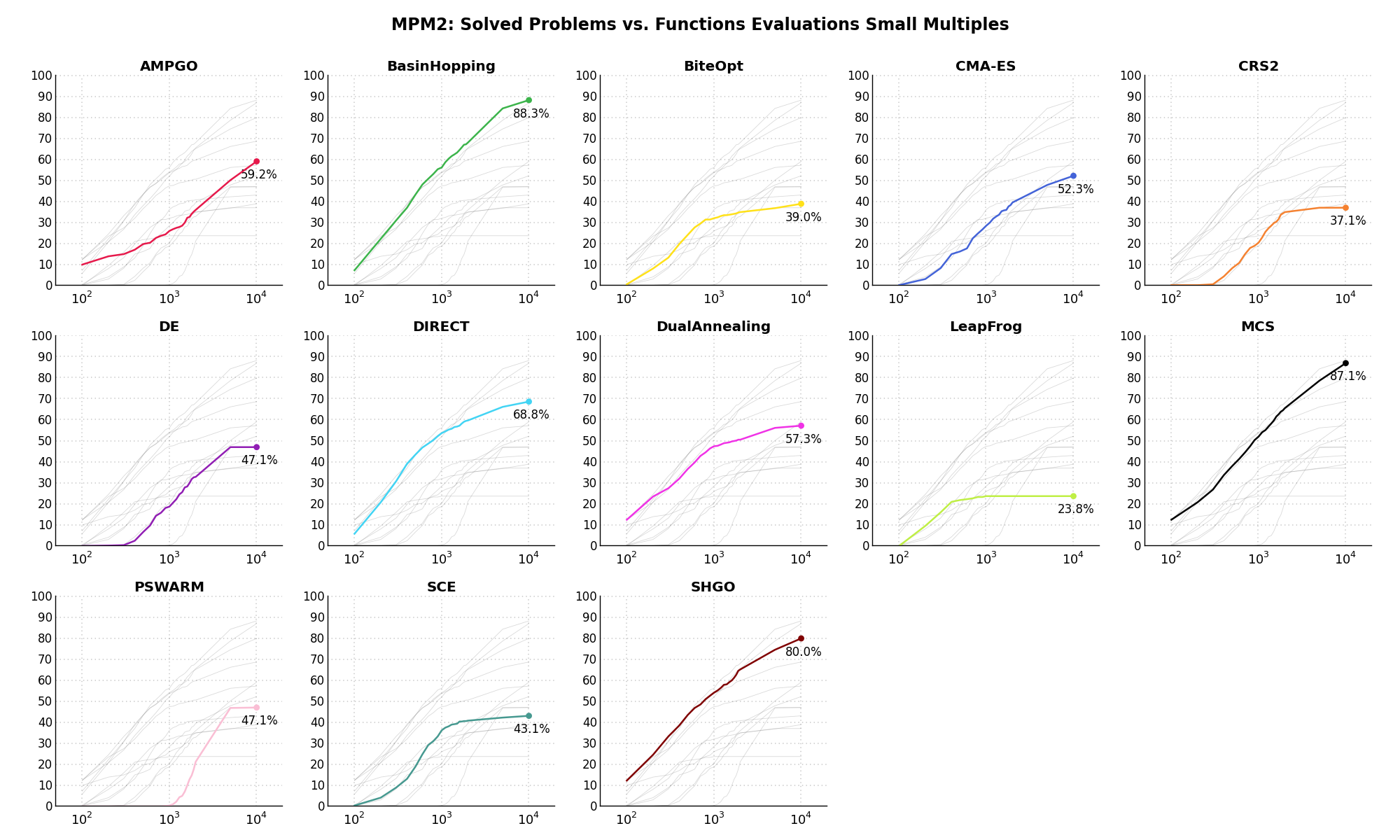
Figure 9.4: Percentage of problems solved given a fixed number of function evaluations on the MPM2 test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 9.5 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
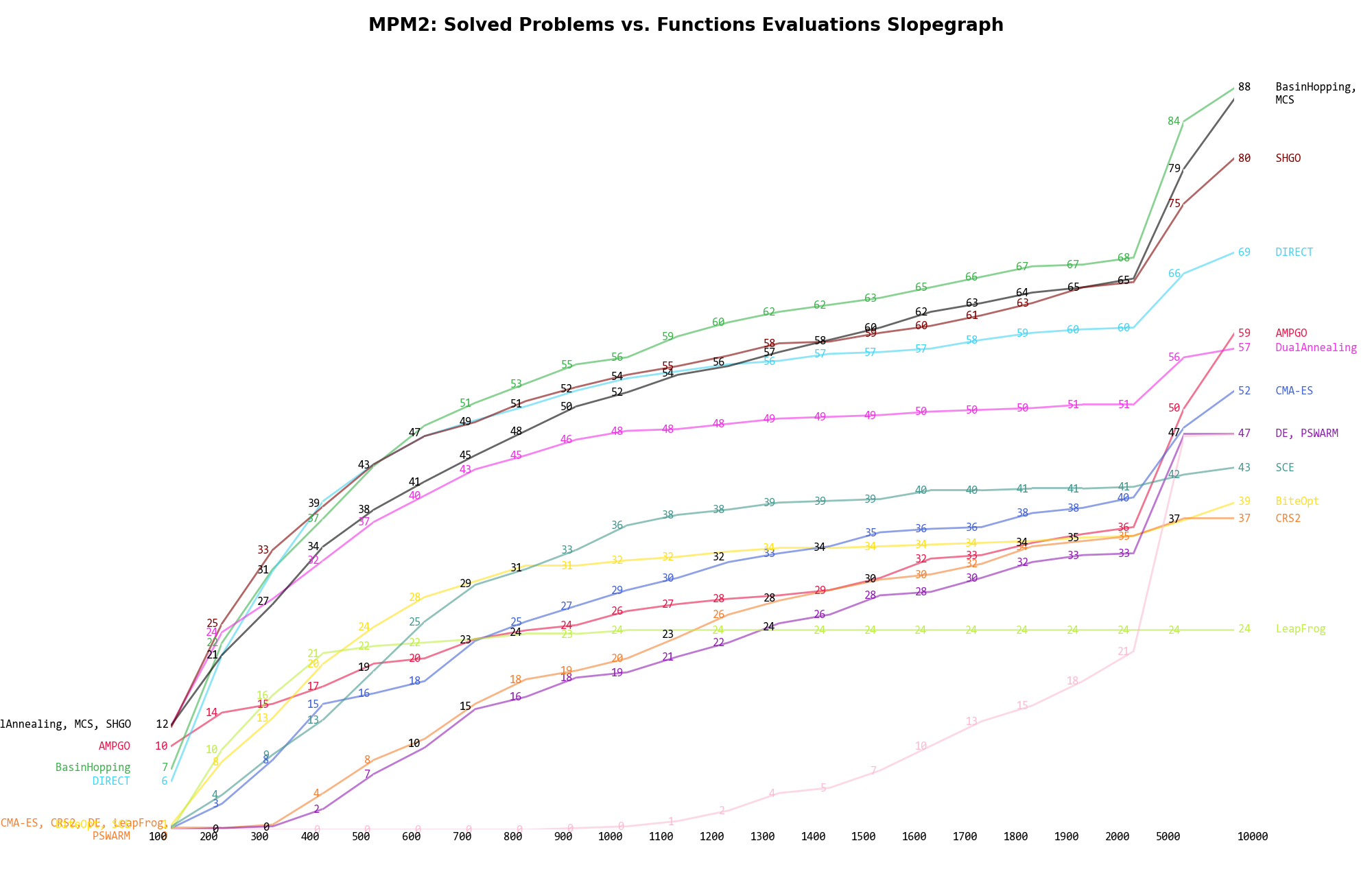
Figure 9.5: Percentage of problems solved given a fixed number of function evaluations on the MPM2 test suite
A few obvious conclusions we can draw from these pictures are:
 Dimensionality Effects¶
Dimensionality Effects¶Since I used the MPM2 test suite to generate test functions with dimensionality ranging from 2 to 5, it is interesting to take a look at the solvers performances as a function of the problem dimensionality. Of course, in general it is to be expected that for larger dimensions less problems are going to be solved - although it is not always necessarily so as it also depends on the function being generated. Results are shown in Table 9.3 .
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 65.8 | 32.5 | 29.2 | 16.7 | 36.0 |
| BasinHopping | 94.2 | 70.0 | 62.5 | 45.8 | 68.1 |
| BiteOpt | 68.3 | 28.3 | 27.5 | 15.8 | 35.0 |
| CMA-ES | 63.3 | 41.7 | 35.8 | 17.5 | 39.6 |
| CRS2 | 59.2 | 37.5 | 31.7 | 11.7 | 35.0 |
| DE | 74.2 | 49.2 | 8.3 | 0.0 | 32.9 |
| DIRECT | 96.7 | 75.0 | 49.2 | 18.3 | 59.8 |
| DualAnnealing | 83.3 | 52.5 | 40.8 | 25.8 | 50.6 |
| LeapFrog | 46.7 | 14.2 | 16.7 | 17.5 | 23.8 |
| MCS | 95.0 | 75.8 | 53.3 | 38.3 | 65.6 |
| PSWARM | 55.0 | 20.0 | 8.3 | 1.7 | 21.2 |
| SCE | 71.7 | 40.8 | 30.8 | 20.0 | 40.8 |
| SHGO | 95.8 | 61.7 | 62.5 | 40.8 | 65.2 |
Figure 9.6 shows the same results in a visual way.
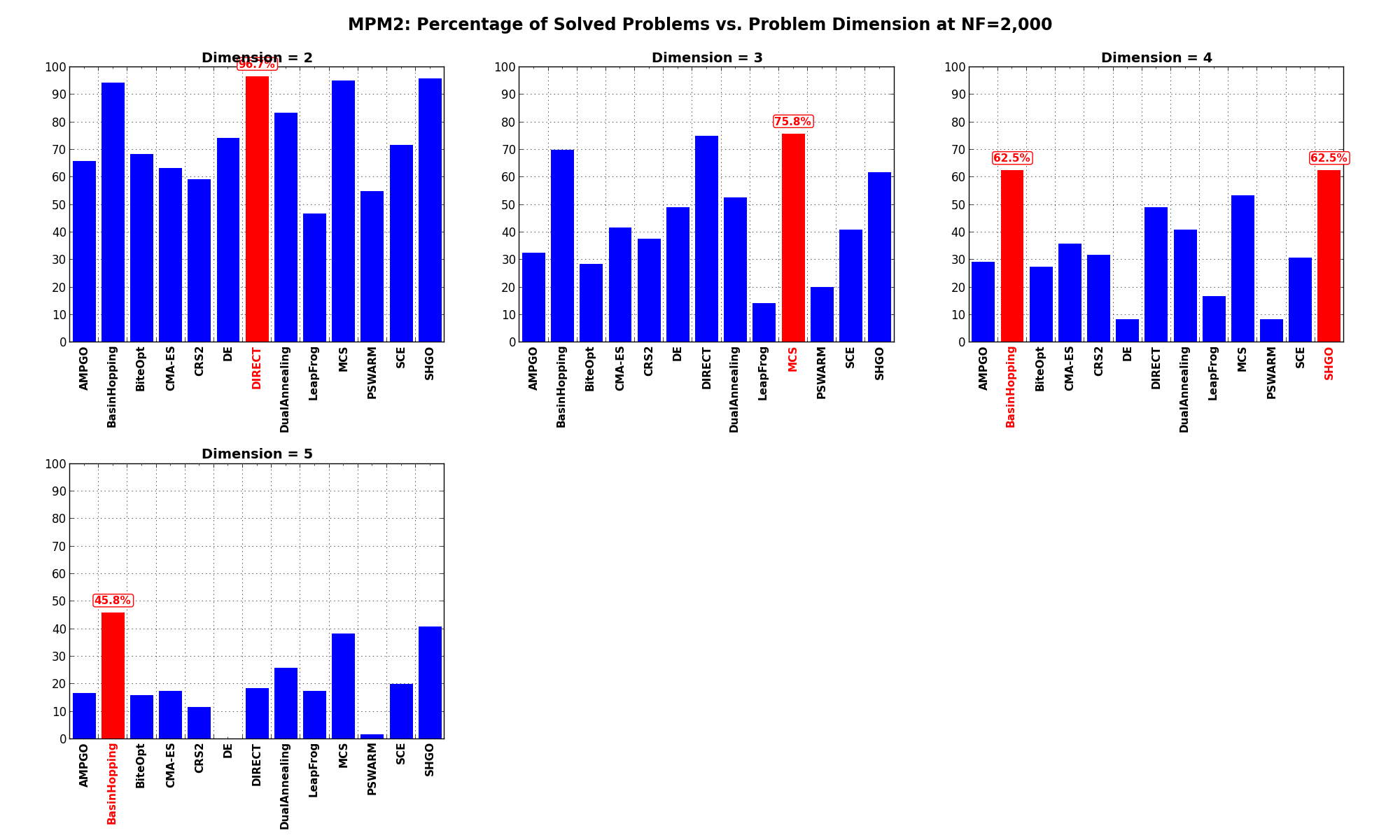
Figure 9.6: Percentage of problems solved as a function of problem dimension for the MPM2 test suite at 
What we can infer from the table and the figure is that, for low dimensionality problems (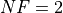 ), very many solvers
are able to solve most of the problems in this test suite, with DIRECT leading the pack. By increasing the dimensionality
other solvers catch up ( MCS, SHGO and BasinHopping).
), very many solvers
are able to solve most of the problems in this test suite, with DIRECT leading the pack. By increasing the dimensionality
other solvers catch up ( MCS, SHGO and BasinHopping).
Pushing the available budget to a very generous  shows MCS and DIRECT solving all problems
for
shows MCS and DIRECT solving all problems
for 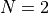 . MCS remains competitive even at higher dimensions but BasinHopping is the clear winner on all problems.
. MCS remains competitive even at higher dimensions but BasinHopping is the clear winner on all problems.
The results for the benchmarks at  are displayed in Table 9.4 and Figure 9.7.
are displayed in Table 9.4 and Figure 9.7.
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 86.7 | 60.8 | 50.0 | 39.2 | 59.2 |
| BasinHopping | 96.7 | 93.3 | 86.7 | 76.7 | 88.3 |
| BiteOpt | 74.2 | 36.7 | 29.2 | 15.8 | 39.0 |
| CMA-ES | 70.0 | 51.7 | 49.2 | 38.3 | 52.3 |
| CRS2 | 59.2 | 38.3 | 31.7 | 19.2 | 37.1 |
| DE | 74.2 | 54.2 | 39.2 | 20.8 | 47.1 |
| DIRECT | 100.0 | 78.3 | 64.2 | 32.5 | 68.8 |
| DualAnnealing | 91.7 | 64.2 | 43.3 | 30.0 | 57.3 |
| LeapFrog | 46.7 | 14.2 | 16.7 | 17.5 | 23.8 |
| MCS | 100.0 | 93.3 | 80.8 | 74.2 | 87.1 |
| PSWARM | 78.3 | 49.2 | 37.5 | 23.3 | 47.1 |
| SCE | 73.3 | 46.7 | 32.5 | 20.0 | 43.1 |
| SHGO | 99.2 | 83.3 | 68.3 | 69.2 | 80.0 |
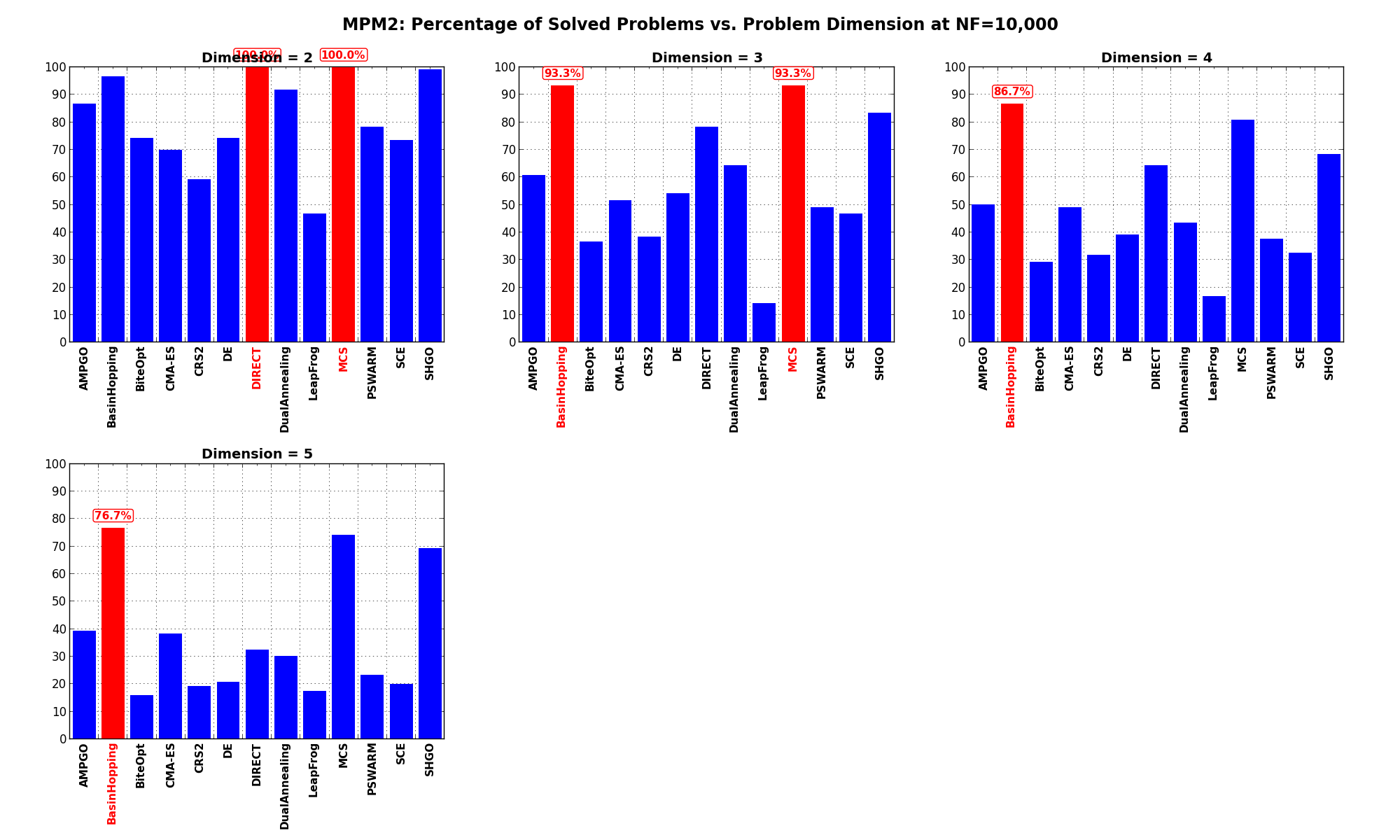
Figure 9.7: Percentage of problems solved as a function of problem dimension for the MPM2 test suite at 