NLSE¶

F_opt Known	X_opt Known	Difficulty
Yes	Yes	Easy

The realm of nonlinear systems of equations is not 100% tailored to global optimization algorithms; nevertheless, nothing stops you from applying a global solver to try and optimize a system of nonlinear equations, assuming the formulation is appropriate for the solvers.

Methodology¶

In order to build this dataset I have drawn from many different sources (Publications, ALIAS/COPRIN and many others) to create 44 systems of nonlinear equations with dimensionality ranging from 2 to 8. A complete set of formulas giving the actual equations is presented in the section NLSE Datasets, and specifically in Table 14.4 .

The approach for building a single-valued objective function out of a system of nonlinear equations:

$\begin{cases} f_1 (x) = ... \\ f_2 (x) = ... \\ ... \\ f_n (x) = ... \end{cases}$

Is to treat it kind of like a nonlinear least squares problem, where the actual (scalar-valued) objective function is easily formulated as:

$F(x) = \sum_{i=1}^n f_i (x)^2$

Then, of course, the global minimum is attained at 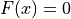$F(x) = 0$ .

A few examples of 2D benchmark functions created with the NLSE test suite can be seen in Figure 14.1.

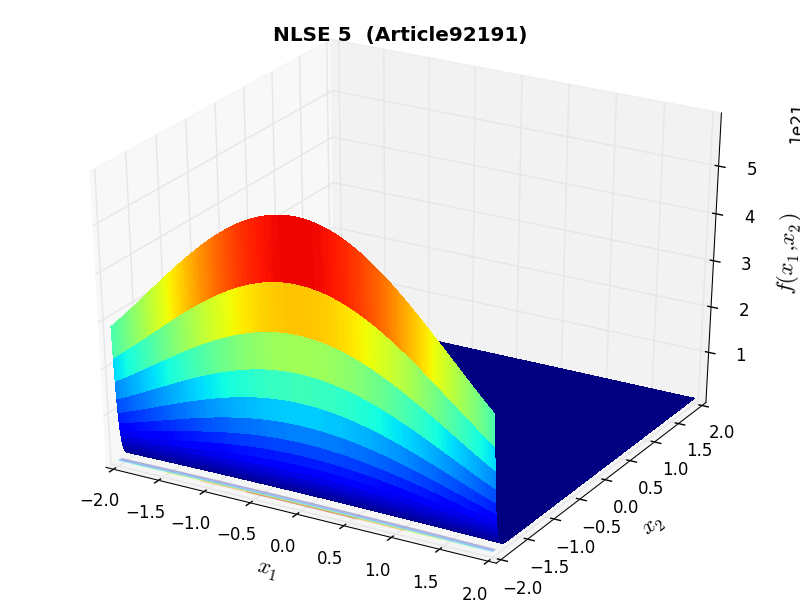
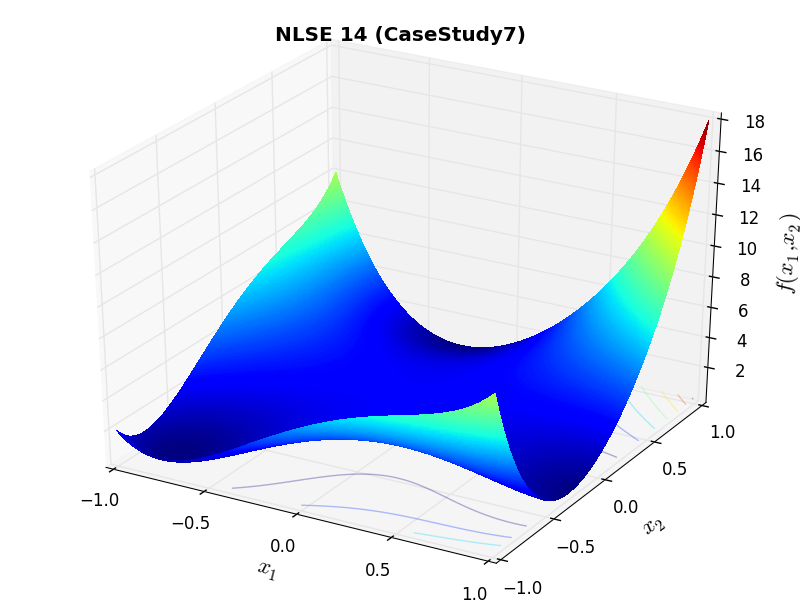
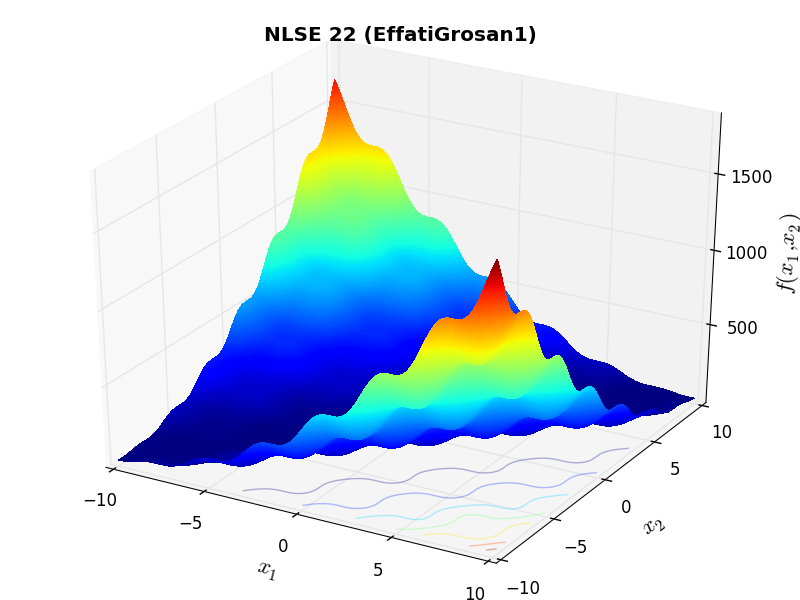
NLSE Function Article92191	NLSE Function CaseStudy7	NLSE Function EffatiGrosan1
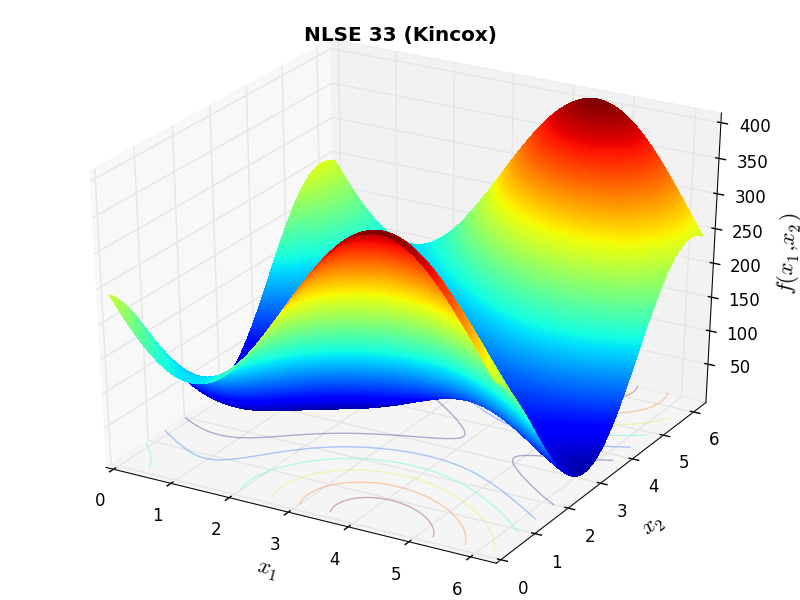
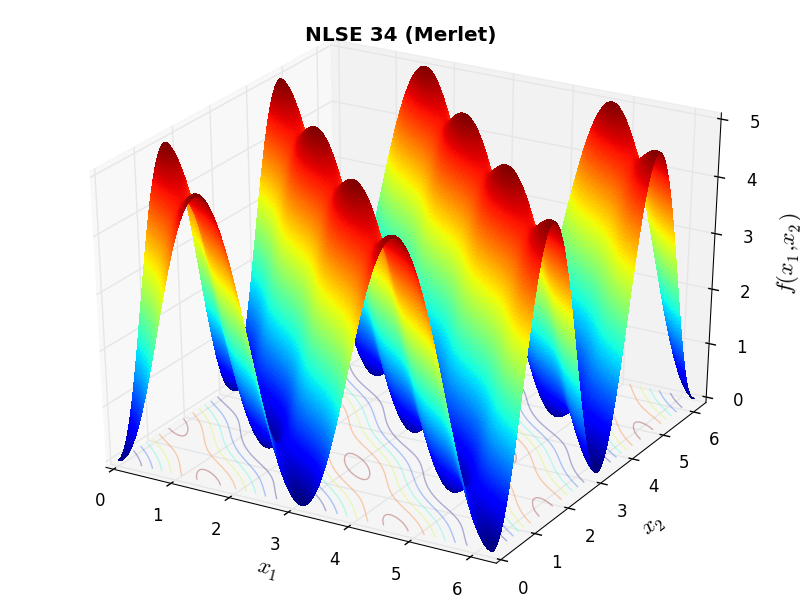
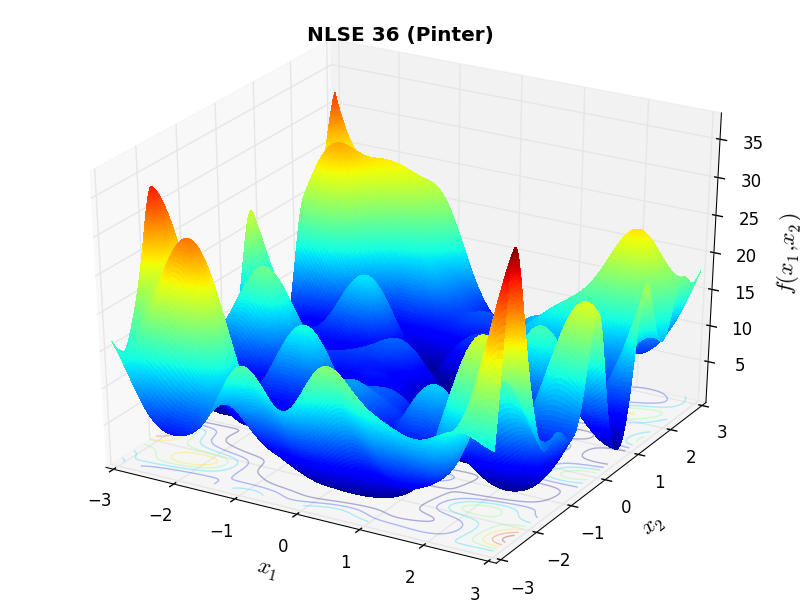
NLSE Function Kincox	NLSE Function Merlet	NLSE Function Pinter

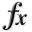General Solvers Performances¶

Table 14.1 below shows the overall success of all Global Optimization algorithms, considering every benchmark function, for a maximum allowable budget of 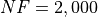$NF = 2,000$ .

The NLSE benchmark suite is an easy test suite: the best solver for 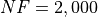$NF = 2,000$ is MCS, with a success rate of 79.6%, but many solvers are able to correctly optimize more than 60% of objectiv functions:: BiteOpt, AMPGO, SHGO, BasinHopping and SCE.

Note

The reported number of functions evaluations refers to successful optimizations only.

**Table 14.1**: Solvers performances on the NLSE benchmark suite at NF = 2,000
Optimization Method	Overall Success (%)	Functions Evaluations
AMPGO	63.64%	321
BasinHopping	63.64%	342
BiteOpt	75.00%	490
CMA-ES	52.27%	622
CRS2	38.64%	801
DE	45.45%	1,234
DIRECT	47.73%	433
DualAnnealing	56.82%	132
LeapFrog	54.55%	412
MCS	79.55%	195
PSWARM	27.27%	1,215
SCE	61.36%	811
SHGO	65.91%	257

These results are also depicted in Figure 14.2, which shows that MCS is the better-performing optimization algorithm, followed by very many other solvers with similar performances.

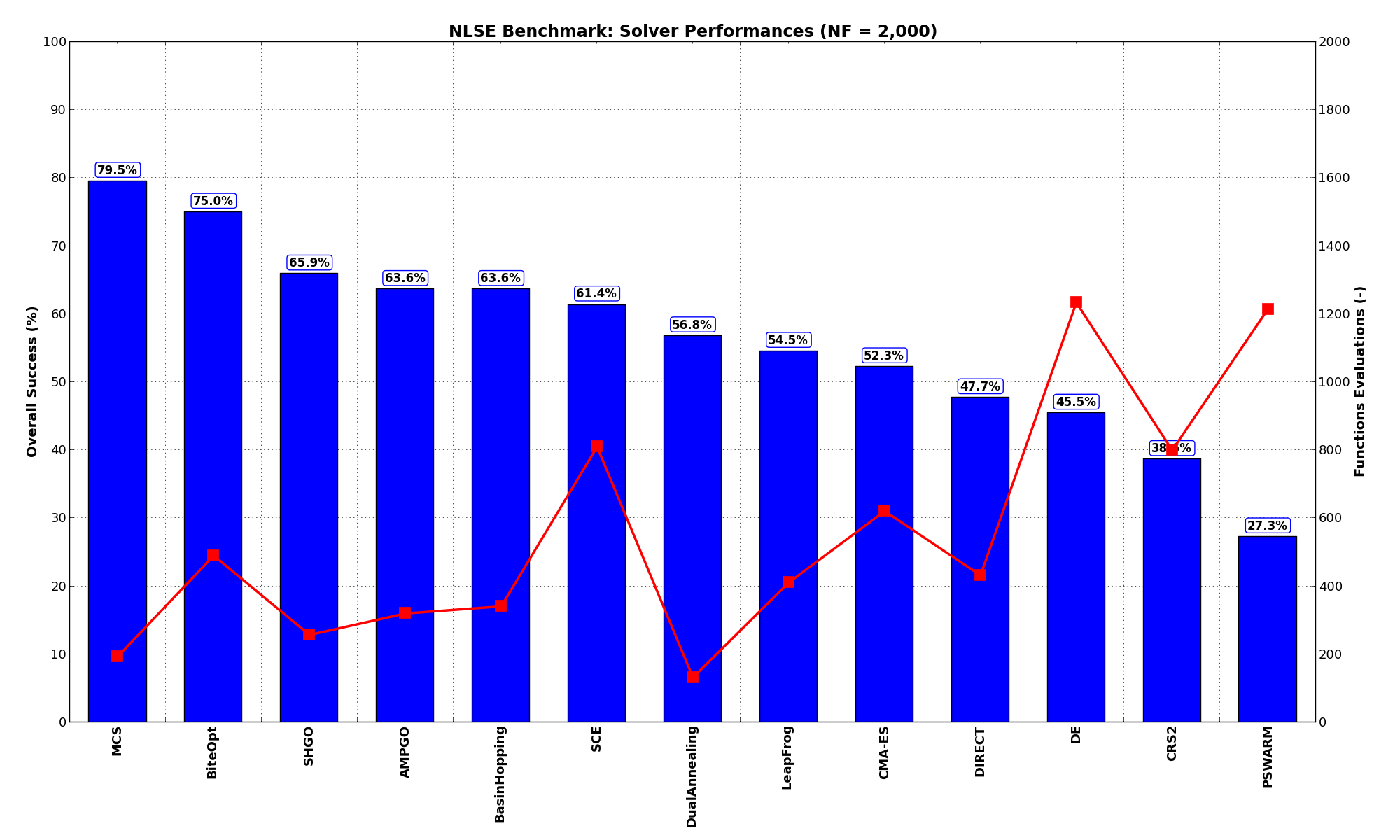
Optimization algorithms performances on the NLSE test suite at :math:`NF = 2,000`

Figure 14.2: Optimization algorithms performances on the NLSE test suite at 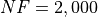$NF = 2,000$

Pushing the available budget to a very generous 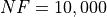$NF = 10,000$ , the results show MCS basically solving all the problems at a 95.5% success rate, with BiteOpt now much closer and AMPGO trailing in third place. The results are also shown visually in Figure 14.3.

**Table 14.2**: Solvers performances on the NLSE benchmark suite at NF = 10,000
Optimization Method	Overall Success (%)	Functions Evaluations
AMPGO	75.00%	999
BasinHopping	68.18%	683
BiteOpt	90.91%	1,061
CMA-ES	59.09%	1,146
CRS2	52.27%	1,645
DE	65.91%	2,306
DIRECT	52.27%	974
DualAnnealing	61.36%	373
LeapFrog	65.91%	1,234
MCS	95.45%	910
PSWARM	54.55%	2,423
SCE	68.18%	970
SHGO	65.91%	257

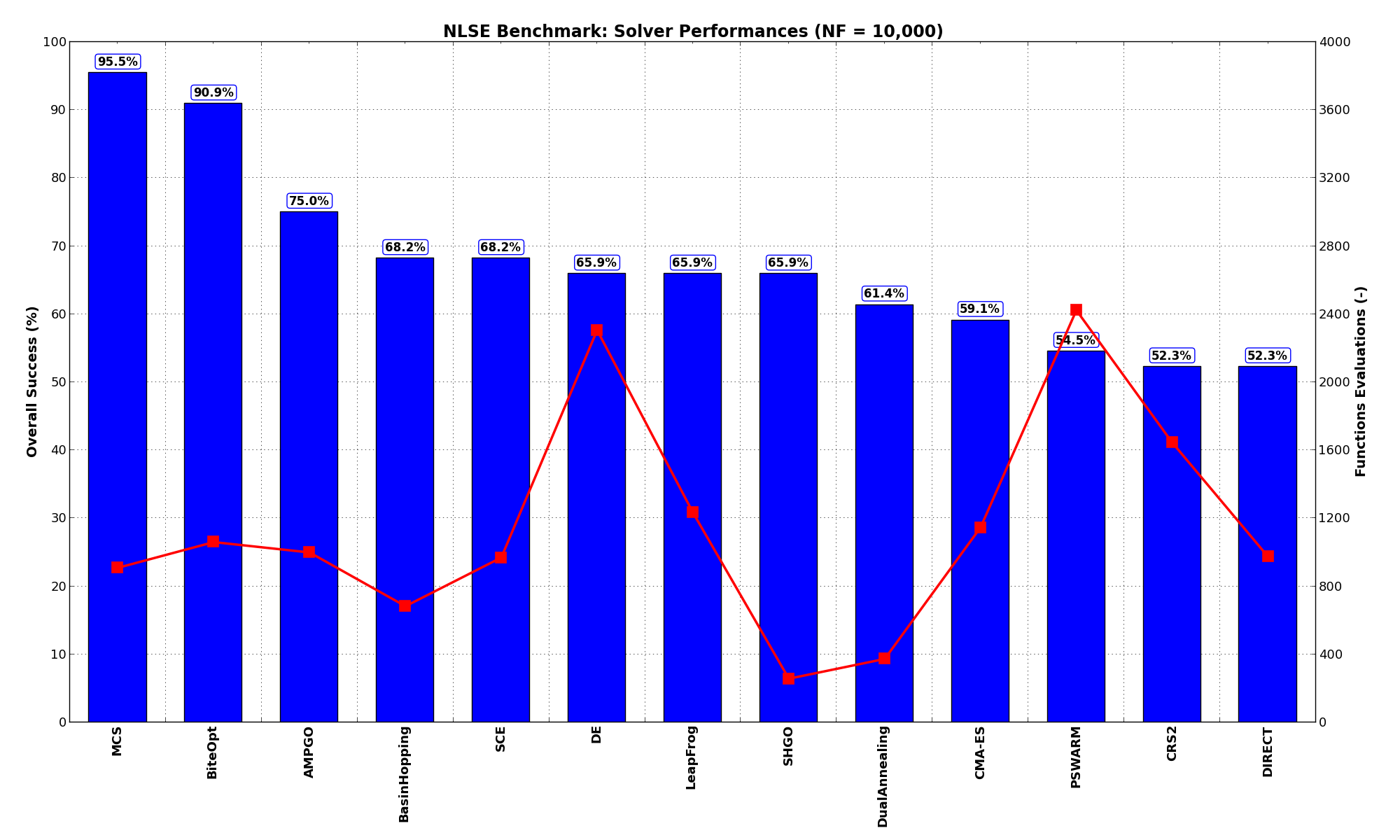
Optimization algorithms performances on the NLSE test suite at :math:`NF = 10,000`

Figure 14.3: Optimization algorithms performances on the NLSE test suite at $NF = 10,000$

Sensitivities on Functions Evaluations Budget¶

It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.

In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.

This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 14.4.

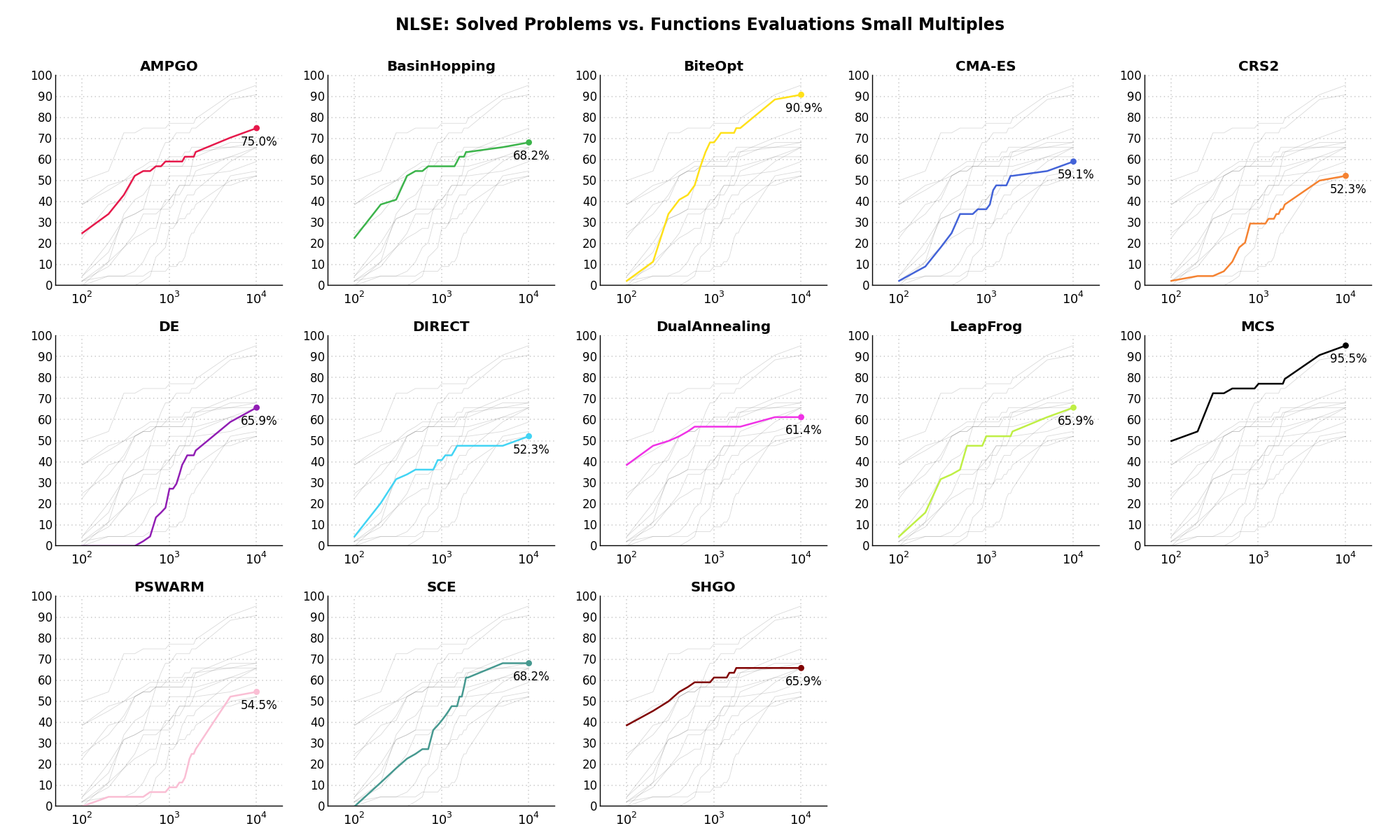
Figure 14.4: Percentage of problems solved given a fixed number of function evaluations on the NLSE test suite

The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 14.5 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.

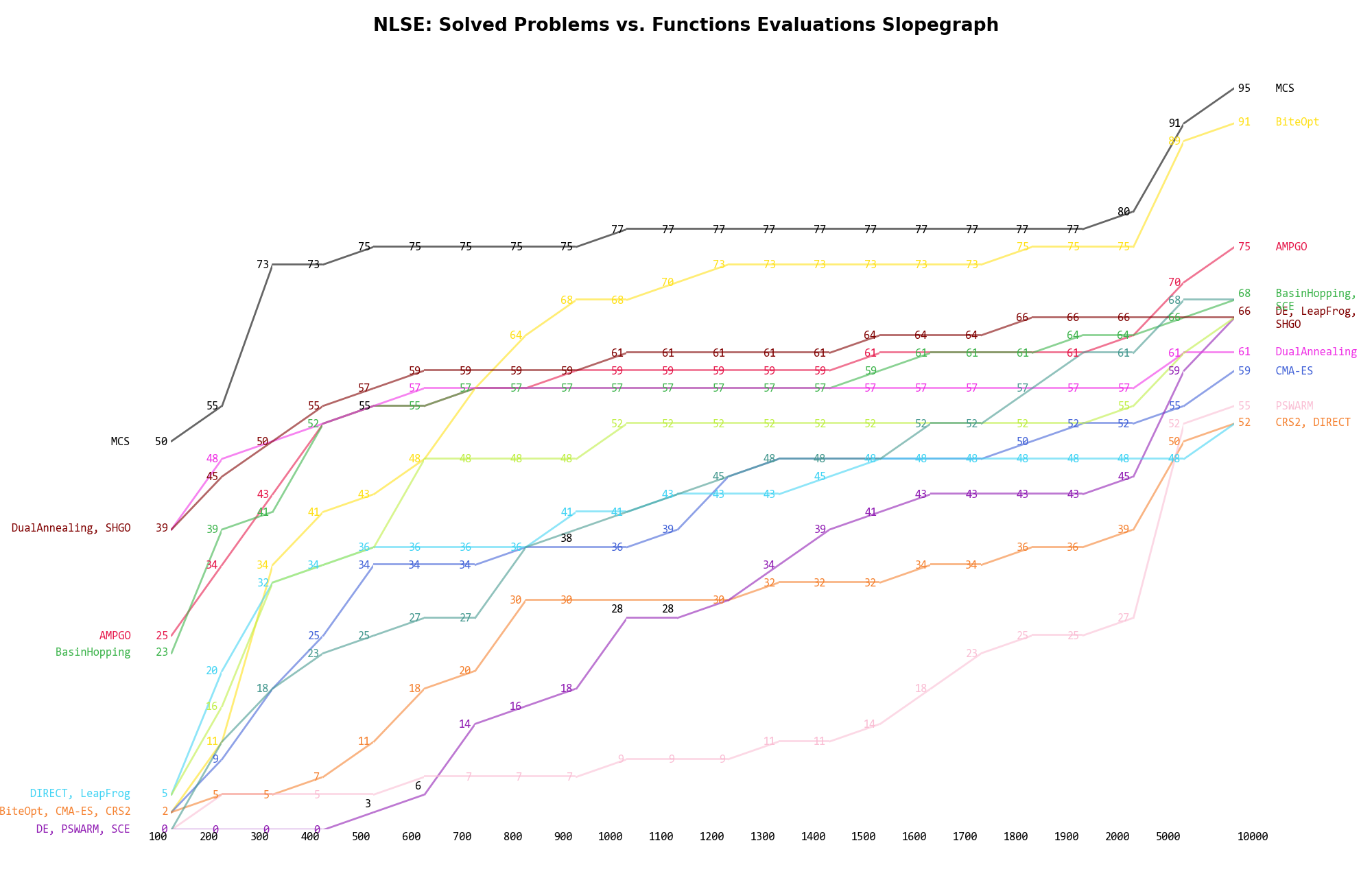
Figure 14.5: Percentage of problems solved given a fixed number of function evaluations on the NLSE test suite

A few obvious conclusions we can draw from these pictures are:

For this specific benchmark test suite, MCS is the best solver no matter the budgets of function evaluations. For very limited budgets, DualAnnealing an SHGO are also good choices.
For medium to large number of functions evaluations, MCS and BiteOpt are by far the best solvers, both achieving more than 90% success rate.

NLSE Datasets¶

**Table 14.4**: NLSE dataset summary
Name	Dimension	Function
AOLcosh1	3	$\begin{cases} y_1 = x \cosh{\left (y + 1.0 / x \right )} + z - 1.0 \\ y_2 = x \cosh{\left (y + 2.0 / x \right )} + z - 4.0 \\ y_3 = x \cosh{\left (y + 3.0 / x \right )} + z - 9.0 \\ \end{cases}$
Article89741	3	$\begin{cases} y_1 = - x + 0.111111111111111 y^{2} + \sin{\left (z \right )} / 3 - 0.0123456790123457 \cos{\left (x \right )} \\ y_2 = - y + 0.333333333333333 \sin{\left (x \right )} + 0.333333333333333 \cos{\left (z \right )} \\ y_3 = 0.333333333333333 y - z + 0.166666666666667 \sin{\left (z \right )} - 0.111111111111111 \cos{\left (x \right )} \\ \end{cases}$
Article90897	2	$\begin{cases} y_1 = x_{1} - 1.7929755 \cdot 10^{-5} x_{2}^{2.0} \\ y_2 = x_{2} - \frac{90.0}{- x_{1} + 1.0} \\ \end{cases}$
Article92191	2	$\begin{cases} y_1 = -32.0 + 0.3 e^{- 13.0 b} \cos{\left (13.0 a \right )} + 0.7 e^{- 12.0 b} \cos{\left (12.0 a \right )} \\ y_2 = 0.3 e^{- 13.0 b} \sin{\left (13.0 a \right )} + 0.7 e^{- 12.0 b} \sin{\left (12.0 a \right )} \\ \end{cases}$
Auto2Fit1	3	$\begin{cases} y_1 = - x y \sin{\left (z \right )} + x / y z + \left(x + y - z\right)^{\cos{\left (x - 1 \right )}} + \left(\left(x - 0.3\right)^{y}\right)^{z} - 1.0 \\ y_2 = - y z \sin{\left (x \right )} + \left(- x + y + z\right)^{\cos{\left (y - 2 \right )}} + \left(\left(y - 0.2\right)^{z}\right)^{x} - 2.0 + y / x z \\ y_3 = - x z \sin{\left (y \right )} + \left(x - y + z\right)^{\cos{\left (z - 3 \right )}} + \left(\left(z - 0.1\right)^{x}\right)^{y} - 3.0 + z / x y \\ \end{cases}$
Auto2Fit2	3	$\begin{cases} y_1 = 2.0^{\sin{\left (y \right )}} + x^{2.23} - z - 1.25 \\ y_2 = 2 x + y + 5.5 z - 7 \\ y_3 = x - y + 0.2 z \\ \end{cases}$
Bronstein	3	$\begin{cases} y_1 = x^{2} + y^{2} + z^{2} - 36.0 \\ y_2 = x + y - z \\ y_3 = x y + z^{2.0} - 1.0 \\ \end{cases}$
Bullard	2	$\begin{cases} y_1 = 10000.0 x_{1} x_{2} - 1.0 \\ y_2 = -1.001 + e^{- x_{2}} + e^{- x_{1}} \\ \end{cases}$
Butcher8	8	$\begin{cases} y_1 = - a - b + b_{1} + b_{2} + b_{3} \\ y_2 = a b - b^{2} - 0.5 b + b_{2} c_{2} + b_{3} c_{3} - 0.5 \\ y_3 = - a \left(b^{2} + 0.333333333333333\right) + b^{3} + b^{2} + 1.33333333333333 b + b_{2} c_{2}^{2} + b_{3} c_{3}^{2} \\ y_4 = - a \left(b^{2} + 0.5 b + 0.166666666666667\right) + a_{32} b_{3} c_{2} + b^{3} + b^{2} + 0.666666666666667 b \\ y_5 = a \left(b^{3} + b\right) - b^{4} - 1.5 b^{3} - 2.5 b^{2} - 0.25 b + 83.0 b_{2} c_{2} + b_{3} c_{3}^{3} - 0.25 \\ y_6 = a \left(b^{3} + 0.5 b^{2} + 0.5 b\right) + a_{32} b_{3} c_{2} c_{3} - b^{4} - 1.5 b^{3} - 1.75 b^{2} - 0.375 b - 0.125 \\ y_7 = a \left(b^{3} + b^{2} + 0.666666666666667 b\right) + a_{32} b_{3} c_{2}^{2} - b^{4} - 1.5 b^{3} - 1.16666666666667 b^{2} - 0.0833333333333333 b - 0.0833333333333333 \\ y_8 = - a \left(b^{3} + b^{2} + 0.333333333333333 b\right) + b^{4} + 1.5 b^{3} + 1.08333333333333 b^{2} + 0.291666666666667 b + 0.0416666666666667 \\ \end{cases}$
CSTR	2	$\begin{cases} y_1 = x_{1} - \left(- R + 1.0\right) \left(\frac{D}{10.0 \beta_{1} + 10.0} - x_{1}\right) e^{\frac{10.0 x_{1}}{1.0 + 10.0 x_{1} / \gamma_{1}}} \\ y_2 = x_{1} - x_{2} \left(\beta_{2} + 1\right) + \left(- R + 1.0\right) \left(0.1 D - \beta_{1} x_{1} - x_{2} \left(- \beta_{2} + 1.0\right)\right) e^{\frac{10.0 x_{2}}{1.0 + 10.0 x_{2} / \gamma_{1}}} \\ \end{cases}$
CaseStudy3	6	$\begin{cases} y_1 = x_{1} + 0.25 x_{2}^{4.0} x_{4} x_{6} + 0.75 \\ y_2 = x_{2} + 1.10090414052591 e^{x_{1} x_{2}} - 1.405 \\ y_3 = x_{3} - 0.5 x_{4} x_{6} + 1.5 \\ y_4 = x_{4} - 0.605 e^{- x_{3}^{2.0} + 1} - 0.395 \\ y_5 = - 0.5 x_{2} x_{6} + x_{5} + 1.5 \\ y_6 = - x_{1} x_{5} + x_{6} \\ \end{cases}$
CaseStudy4	3	$\begin{cases} y_1 = - 5.0 x_{1} x_{2} x_{3} + x_{1}^{x_{2}} + x_{2}^{x_{1}} - 85.0 \\ y_2 = x_{1}^{3.0} - x_{2}^{x_{3}} - x_{3}^{x_{2}} - 60.0 \\ y_3 = x_{1}^{x_{3}} - x_{2} + x_{3}^{x_{1}} - 2 \\ \end{cases}$
CaseStudy5	3	$\begin{cases} y_1 = - 8.0 x_{1} \sin{\left (x_{2} \right )} + e^{x_{1}^{2.0}} \\ y_2 = x_{1} + x_{2} - 1.0 \\ y_3 = \left(x_{3} - 1.0\right)^{3.0} \\ \end{cases}$
CaseStudy6	3	$\begin{cases} y_1 = 3.0 x_{1} - \cos{\left (x_{2} x_{3} \right )} - 0.5 \\ y_2 = x_{1}^{2.0} - 625.0 x_{2}^{2.0} - 0.25 \\ y_3 = 20.0 x_{3} - 1.0 + 3.33333333333333 \pi + e^{- x_{1} x_{2}} \\ \end{cases}$
CaseStudy7	2	$\begin{cases} y_1 = - 3.0 x_{1} x_{2}^{2.0} + x_{1}^{3.0} - 1.0 \\ y_2 = 3.0 x_{1}^{2.0} x_{2} - x_{2}^{3.0} + 1.0 \\ \end{cases}$
Celestial	3	$\begin{cases} y_1 = 4 p^{3} \phi^{3} - 6 p^{3} - 12 p^{2} \phi^{3} s + 15 p \phi^{3} s^{3} - 3 p \phi^{3} s - 3 \phi^{3} s^{5} + \phi^{3} s^{3} \\ y_2 = - 6 p^{3} s - 9 p \phi^{3} s^{2} + 5 p \phi^{3} + 3 \phi^{3} s^{4} - 5 \phi^{3} s^{2} \\ y_3 = - 12 p s^{2} + 12 p + 4 \phi^{2} + 3 s^{4} - 6 s^{2} + 3 \\ \end{cases}$
Chem	5	$\begin{cases} y_1 = - x_{1} \left(x_{2} + 1\right) + 3 x_{5} \\ y_2 = - r x_{5} + x_{1} + x_{2} \left(2 r_{10} x_{2} + r_{7} x_{3} + r_{8} + r_{9} x_{4} + 2 x_{1} + x_{3}^{2}\right) \\ y_3 = x_{3} \left(2 r_{5} x_{3} + r_{6} + r_{7} x_{2} + 2 x_{2} x_{3}\right) - 8 x_{5} \\ y_4 = - 4 r x_{5} + x_{4} \left(r_{9} x_{2} + 2 x_{4}\right) \\ y_5 = r_{5} x_{3}^{2} + r_{6} x_{3} + x_{1} + x_{2} \left(r_{10} x_{2} + r_{7} x_{3} + r_{8} + r_{9} x_{4} + x_{1} + x_{3}^{2}\right) + x_{4}^{2} - 1 \\ \end{cases}$
Chemk	4	$\begin{cases} y_1 = x_{1}^{2} - x_{2} \\ y_2 = - x_{3} + x_{4}^{2} \\ y_3 = 0.55 x_{1} x_{4} + 0.45 x_{1} - 16970000.0 x_{2} x_{4} + 21770000.0 x_{2} - x_{4} \\ y_4 = 41260000.0 x_{1} x_{3} - 8282000.0 x_{1} x_{4} + 158500000000000.0 x_{2} x_{4} + 22840000.0 x_{3} x_{4} - 19180000.0 x_{3} + 48.4 x_{4} - 27.73 \\ \end{cases}$
Cyclo	3	$\begin{cases} y_1 = - y^{2} z^{2} - y^{2} + 24 y z - z^{2} - 13 \\ y_2 = - x^{2} z^{2} - x^{2} + 24 x z - z^{2} - 13 \\ y_3 = - x^{2} y^{2} - x^{2} + 24 x y - y^{2} - 13 \\ \end{cases}$
DiGregorio	3	$\begin{cases} y_1 = \left(40 \sin{\left (p \right )} - 40.0\right)^{2.0} + \left(q - 40.0 \cos{\left (p \right )} + 10.0\right)^{2.0} - 1000.0 \\ y_2 = \left(- 40 \cos{\left (p \right )} + 20.0\right)^{2.0} - \left(- 35.0 \cos{\left (t \right )} + 20.0\right)^{2.0} + 1600.0 \sin^{2.0}{\left (p \right )} - 1225.0 \sin^{2.0}{\left (t \right )} \\ y_3 = \left(- q + 10\right)^{2.0} - \left(- 35 \cos{\left (t \right )} - 10\right)^{2.0} - 1225.0 \sin^{2.0}{\left (t \right )} + 1600.0 \\ \end{cases}$
Dipole	8	$\begin{cases} y_1 = a + b - 0.63254 \\ y_2 = c + d + 1.34534 \\ y_3 = a t + b u - c v - d w + 0.8365348 \\ y_4 = a v + b w + c t + d u - 1.7345334 \\ y_5 = a t^{2} - a v^{2} + b u^{2} - b w^{2} - 2 c t v - 2 d u w - 1.352352 \\ y_6 = 2 a t v + 2 b u w + c t^{2} - c v^{2} + d u^{2} - d w^{2} + 0.843453 \\ y_7 = a t^{3} - 3 a t v^{2} + b u^{3} - 3 b u w^{2} - 3 c t^{2} v + c v^{3} - 3 d u^{2} w + d w^{3} + 0.9563453 \\ y_8 = 3 a t^{2} v - a v^{3} + 3 b u^{2} w - b w^{3} + c t^{3} - 3 c t v^{2} + d u^{3} - 3 d u w^{2} - 1.2342523 \\ \end{cases}$
Eco9	8	$\begin{cases} y_1 = x_{1} + x_{2} \left(x_{1} + x_{3}\right) + x_{4} \left(x_{3} + x_{5}\right) + x_{6} \left(x_{5} + x_{7}\right) - x_{8} \left(- x_{7} + 0.125\right) \\ y_2 = x_{2} + x_{3} \left(x_{1} + x_{5}\right) + x_{4} \left(x_{2} + x_{6}\right) + x_{5} x_{7} - x_{8} \left(- x_{6} + 0.25\right) \\ y_3 = x_{2} x_{5} + x_{3} \left(x_{6} + 1\right) + x_{4} \left(x_{1} + x_{7}\right) - x_{8} \left(- x_{5} + 0.375\right) \\ y_4 = x_{1} x_{5} + x_{2} x_{6} + x_{3} x_{7} + x_{4} - x_{8} \left(- x_{4} + 0.5\right) \\ y_5 = x_{1} x_{6} + x_{2} x_{7} + x_{5} - x_{8} \left(- x_{3} + 0.625\right) \\ y_6 = x_{1} x_{7} + x_{6} - x_{8} \left(- x_{2} + 75.0\right) \\ y_7 = x_{7} - x_{8} \left(- x_{1} + 0.875\right) \\ y_8 = x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} + 1.0 \\ \end{cases}$
EffatiGrosan1	2	$\begin{cases} y_1 = \cos{\left (2 x_{1} \right )} - \cos{\left (2 x_{2} \right )} - 0.4 \\ y_2 = - 2 x_{1} + 2 x_{2} - \sin{\left (2 x_{1} \right )} + \sin{\left (2 x_{2} \right )} - 1.2 \\ \end{cases}$
EffatiGrosan2	2	$\begin{cases} y_1 = x_{1} x_{2} + e^{x_{1}} - 1.0 \\ y_2 = x_{1} + x_{2} + \sin{\left (x_{1} x_{2} \right )} - 1.0 \\ \end{cases}$
F3	2	$\begin{cases} y_1 = 3.0 x_{1} x_{2} + 2.0 x_{1} - 1.0 \\ y_2 = x_{1} - x_{2} + x_{2} e^{- x_{1}} - e^{-1} \\ \end{cases}$
Ferrais	2	$\begin{cases} y_1 = 0.5 x_{1} + 0.25 x_{2} / \pi - 0.5 \sin{\left (x_{1} x_{2} \right )} \\ y_2 = - 5.43656365691809 x_{1} + 2.71828182845905 x_{2} / \pi + \left(- 0.25 / \pi + 1.0\right) \left(e^{2.0 x_{1}} - 2.71828182845905\right) \\ \end{cases}$
Gaussian	3	$\begin{cases} y_1 = 0.0009 \\ y_2 = 0.0044 \\ y_3 = 0.0175 \\ y_1 = x_{1} e^{- 0.5 x_{2} \left(t_{1} - x_{3}\right)^{2.0}} - y_{11} \\ y_2 = x_{2} e^{- 0.5 x_{2} \left(t_{2} - x_{3}\right)^{2.0}} - y_{22} \\ y_3 = x_{3} e^{- 0.5 x_{2} \left(t_{3} - x_{3}\right)^{2.0}} - y_{33} \\ \end{cases}$
GenEig	6	$\begin{cases} y_1 = - 10 x_{1} x_{6}^{2} + x_{1} x_{6} + 10 x_{1} + 2 x_{2} x_{6}^{2} + 2 x_{2} x_{6} + 2 x_{2} - x_{3} x_{6}^{2} + x_{3} x_{6} - x_{3} + x_{4} x_{6}^{2} + 2 x_{4} x_{6} + 2 x_{4} + 3 x_{5} x_{6}^{2} + x_{5} x_{6} - 2 x_{5} \\ y_2 = 2 x_{1} x_{6}^{2} + 2 x_{1} x_{6} + 2 x_{1} - 11 x_{2} x_{6}^{2} + x_{2} x_{6} + 9 x_{2} + 2 x_{3} x_{6}^{2} + 2 x_{3} x_{6} + 3 x_{3} - 2 x_{4} x_{6}^{2} + x_{4} x_{6} - x_{4} + x_{5} x_{6}^{2} + 3 x_{5} x_{6} - 2 x_{5} \\ y_3 = - x_{1} x_{6}^{2} + x_{1} x_{6} - x_{1} + 2 x_{2} x_{6}^{2} + 2 x_{2} x_{6} + 3 x_{2} - 12 x_{3} x_{6}^{2} + 10 x_{3} - x_{4} x_{6}^{2} - 2 x_{4} x_{6} + 2 x_{4} + x_{5} x_{6}^{2} - 2 x_{5} x_{6} - x_{5} \\ y_4 = x_{1} x_{6}^{2} + 2 x_{1} x_{6} + 2 x_{1} - 2 x_{2} x_{6}^{2} + x_{2} x_{6} - x_{2} - x_{3} x_{6}^{2} - 2 x_{3} x_{6} + 2 x_{3} - 10 x_{4} x_{6}^{2} + 2 x_{4} x_{6} + 12 x_{4} + 2 x_{5} x_{6}^{2} + 3 x_{5} x_{6} + x_{5} \\ y_5 = 3 x_{1} x_{6}^{2} + x_{1} x_{6} - 2 x_{1} + x_{2} x_{6}^{2} + 3 x_{2} x_{6} - 2 x_{2} + x_{3} x_{6}^{2} - 2 x_{3} x_{6} - x_{3} + 2 x_{4} x_{6}^{2} + 3 x_{4} x_{6} + x_{4} - 11 x_{5} x_{6}^{2} + 3 x_{5} x_{6} + 10 x_{5} \\ y_6 = x_{1} + x_{2} + x_{3} + x_{4} + x_{5} - 1 \\ \end{cases}$
Helical	2	$\begin{cases} y_1 = - 100.0 \arctan{\left (x_{2} / x_{1} \right )} / \pi + 0.5 \\ y_2 = 10.0 \sqrt{x_{1}^{2.0} + x_{2}^{2.0}} - 10.0 \\ \end{cases}$
Helical1	3	$\begin{cases} y_1 = 10 x_{3} + 100.0 \arctan{\left (x_{2} / x_{1} \right )} / \pi - 50.0 \\ y_2 = 10.0 \sqrt{x_{1}^{2.0} + x_{2}^{2.0}} - 10.0 \\ y_3 = x_{1} - \sin{\left (x_{3} \right )} \\ \end{cases}$
Kearl11	8	$\begin{cases} y_1 = x_{1}^{2} + x_{2}^{2} - 1 \\ y_2 = x_{3}^{2} + x_{4}^{2} - 1 \\ y_3 = x_{5}^{2} + x_{6}^{2} - 1 \\ y_4 = x_{7}^{2} + x_{8}^{2} - 1 \\ y_5 = 0.004731 x_{1} x_{3} - 0.1238 x_{1} - 0.3578 x_{2} x_{3} - 0.001637 x_{2} - 0.9338 x_{4} + x_{7} - 0.3571 \\ y_6 = 0.2238 x_{1} x_{3} + 0.2638 x_{1} + 0.7623 x_{2} x_{3} - 0.07745 x_{2} - 0.6734 x_{4} - 0.6022 \\ y_7 = 0.3578 x_{1} + 0.004731 x_{2} + x_{6} x_{8} \\ y_8 = - 0.7623 x_{1} + 0.2238 x_{2} + 0.3461 \\ \end{cases}$
Kin1	6	$\begin{cases} y_1 = \sin{\left (t_{2} \right )} \sin{\left (t_{6} \right )} \cos{\left (t_{5} \right )} - \sin{\left (t_{3} \right )} \sin{\left (t_{6} \right )} \cos{\left (t_{5} \right )} - \sin{\left (t_{4} \right )} \sin{\left (t_{6} \right )} \cos{\left (t_{5} \right )} + \cos{\left (t_{2} \right )} \cos{\left (t_{6} \right )} + \cos{\left (t_{3} \right )} \cos{\left (t_{6} \right )} + \cos{\left (t_{4} \right )} \cos{\left (t_{6} \right )} - 0.4077 \\ y_2 = \sin{\left (t_{1} \right )} \cos{\left (t_{5} \right )} + \sin{\left (t_{5} \right )} \cos{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + \sin{\left (t_{5} \right )} \cos{\left (t_{1} \right )} \cos{\left (t_{3} \right )} + \sin{\left (t_{5} \right )} \cos{\left (t_{1} \right )} \cos{\left (t_{4} \right )} - 1.9115 \\ y_3 = \sin{\left (t_{2} \right )} \sin{\left (t_{5} \right )} + \sin{\left (t_{3} \right )} \sin{\left (t_{5} \right )} + \sin{\left (t_{4} \right )} \sin{\left (t_{5} \right )} - 1.9791 \\ y_4 = 3 \cos{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + 2 \cos{\left (t_{1} \right )} \cos{\left (t_{3} \right )} + \cos{\left (t_{1} \right )} \cos{\left (t_{4} \right )} - 4.0616 \\ y_5 = 3 \sin{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + 2 \sin{\left (t_{1} \right )} \cos{\left (t_{3} \right )} + \sin{\left (t_{1} \right )} \cos{\left (t_{4} \right )} - 1.7172 \\ y_6 = 3 \sin{\left (t_{2} \right )} + 2 \sin{\left (t_{3} \right )} + \sin{\left (t_{4} \right )} - 3.9701 \\ \end{cases}$
Kincox	2	$\begin{cases} y_1 = - 6.0 \sin{\left (t_{1} \right )} \sin{\left (t_{2} \right )} + 6.0 \cos{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + 10.0 \cos{\left (t_{1} \right )} - 1.0 \\ y_2 = 6.0 \sin{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + 10.0 \sin{\left (t_{1} \right )} + 6.0 \sin{\left (t_{2} \right )} \cos{\left (t_{1} \right )} - 4.0 \\ \end{cases}$
Merlet	2	$\begin{cases} y_1 = - \sin{\left (x_{1} \right )} \cos{\left (x_{2} \right )} - 2.0 \sin{\left (x_{2} \right )} \cos{\left (x_{1} \right )} \\ y_2 = - 2.0 \sin{\left (x_{1} \right )} \cos{\left (x_{2} \right )} - \sin{\left (x_{2} \right )} \cos{\left (x_{1} \right )} \\ \end{cases}$
Neuro	6	$\begin{cases} y_1 = x_{1}^{2.0} + x_{3}^{2.0} - 1.0 \\ y_2 = x_{2}^{2.0} + x_{4}^{2.0} - 1.0 \\ y_3 = x_{3}^{3.0} x_{5} + x_{4}^{3.0} x_{6} \\ y_4 = x_{1}^{3.0} x_{5} + x_{2}^{3.0} x_{6} \\ y_5 = x_{1} x_{3}^{2.0} x_{5} + x_{2} x_{4}^{2.0} x_{6} \\ y_6 = x_{1}^{2.0} x_{3} x_{5} + x_{2}^{2.0} x_{4} x_{6} \\ \end{cases}$
Pinter	2	$\begin{cases} y_1 = x_{1} - \sin{\left (2.0 x_{1} + 3.0 x_{2} \right )} - \cos{\left (3.0 x_{1} - 5.0 x_{2} \right )} \\ y_2 = x_{2} - \sin{\left (x_{1} - 2.0 x_{2} \right )} + \cos{\left (x_{1} + 3.0 x_{2} \right )} \\ \end{cases}$
Puma	4	$\begin{cases} y_1 = - 0.3578 \sin{\left (t_{1} \right )} \cos{\left (t_{2} \right )} - 0.001637 \sin{\left (t_{1} \right )} - 0.9338 \sin{\left (t_{2} \right )} + 0.004731 \cos{\left (t_{1} \right )} \cos{\left (t_{2} \right )} - 0.1238 \cos{\left (t_{1} \right )} + \cos{\left (t_{4} \right )} - 0.3571 \\ y_2 = 0.7623 \sin{\left (t_{1} \right )} \cos{\left (t_{2} \right )} - 0.07745 \sin{\left (t_{1} \right )} - 0.6734 \sin{\left (t_{2} \right )} + 0.2238 \cos{\left (t_{1} \right )} \cos{\left (t_{2} \right )} + 0.2638 \cos{\left (t_{1} \right )} - 0.6022 \\ y_3 = 0.004731 \sin{\left (t_{1} \right )} + \sin{\left (t_{3} \right )} \sin{\left (t_{4} \right )} + 0.3578 \cos{\left (t_{1} \right )} \\ y_4 = 0.2238 \sin{\left (t_{1} \right )} - 0.7623 \cos{\left (t_{1} \right )} + 0.3461 \\ \end{cases}$
Semiconductor	6	$\begin{cases} y_1 = x_{2} \\ y_2 = x_{3} \\ y_3 = - V + x_{5} \\ y_4 = - V + x_{6} \\ y_5 = - DDD / ni + e^{a \left(- x_{1} + x_{3}\right)} - e^{a \left(x_{1} - x_{2}\right)} \\ y_6 = DDD / ni + e^{a \left(- x_{4} + x_{6}\right)} - e^{a \left(x_{4} - x_{5}\right)} \\ \end{cases}$
SixBody	6	$\begin{cases} y_1 = B + D - 6 F + \left(B - D\right) \left(3 b - 3 d\right) + 4 \\ y_2 = 5 B - 5 D + \left(3 b - 3 d\right) \left(B + D - 2 F\right) \\ y_3 = - 6 b - 6 d + 4 f + 3 \left(b - d\right)^{2} + 3 \\ y_4 = B^{2} b^{3} - 1 \\ y_5 = D^{2} d^{3} - 1 \\ y_6 = F^{2} f^{3} - 1 \\ \end{cases}$
SjirkBoon	4	$\begin{cases} y_1 = C_{1} \cos{\left (3.0 \phi_{1} \right )} + C_{2} \cos{\left (3.0 \phi_{2} \right )} + 5.0 \\ y_2 = C_{1} \cos{\left (\phi_{1} \right )} + C_{2} \cos{\left (\phi_{2} \right )} - 3.0 \\ y_3 = C_{1} \sin{\left (3.0 \phi_{1} \right )} + C_{2} \sin{\left (3.0 \phi_{2} \right )} \\ y_4 = C_{1} \sin{\left (\phi_{1} \right )} + C_{2} \sin{\left (\phi_{2} \right )} - 4.0 \\ \end{cases}$
ThinWall	3	$\begin{cases} y_1 = b h + \left(b - 2.0 t\right) \left(h - 2.0 t\right) - 165.0 \\ y_2 = 0.0833333333333333 b h^{3.0} - 0.0833333333333333 \left(b - 2.0 t\right) \left(h - 2.0 t\right)^{3.0} - 9369.0 \\ y_3 = \frac{2.0 t \left(b - t\right)^{2.0} \left(h - t\right)^{2.0}}{b + h - 2.0 t} - 6835.0 \\ \end{cases}$
Xu	2	$\begin{cases} y_1 = - x_{1} + 2.0 \sin{\left (x_{1} \right )} + 7 \sin{\left (x_{2} \right )} + 0.8 \cos{\left (2 x_{1} \right )} \\ y_2 = - x_{2} + 4.0 \sin{\left (2 x_{1} \right )} + 1.4 \sin{\left (3 x_{2} \right )} + 3.1 \cos{\left (2 x_{2} \right )} \\ \end{cases}$