Navigation
- index
- next |
- previous |
- Home »
- The Benchmarks »
- CVMG
 CVMG¶
CVMG¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| Yes | No | Medium |
This benchmark test suite represents yet another “landscape generator”, I had to dig it out using the Wayback Machine at http://web.archive.org/web/20100612044104/https://www.cs.uwyo.edu/~wspears/multi.kennedy.html . The acronym stands for “Continuous Valued Multimodality Generator”. The source code is in C++ but it’s fairly easy to port it to Python.
In addition to the original implementation (that uses the Sigmoid as a softmax/transformation function) I have added a few others to create varied landscapes.
 Methodology¶
Methodology¶The objective functions in this test suite are relatively easy to generate. By selecting a number of desired peaks (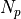 )
and the problem dimension (
)
and the problem dimension (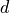 ) we can define a “landscape” function as:
) we can define a “landscape” function as:
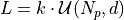
Where  is a user-selectable constant and
is a user-selectable constant and 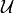 is the uniform distribution over
is the uniform distribution over 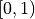 .
.
Then, through the use of a softmax/transformation function 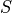 (which can be a sigmoid, or tanh or arctan, etc..., whatever input
vector of parameters (
(which can be a sigmoid, or tanh or arctan, etc..., whatever input
vector of parameters (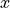 ) is restricted in the interval
) is restricted in the interval ![[-1, 1]](_images/math/5c3818b9565a33fd3aadba10026d32c5e3eea90f.png) , with a function
, with a function 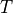 like:
like:
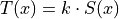
Finally, the objective function is defined as:
![F(x) = \textbf{min} \left [ \sum_{i=1}^d (S(x) - L)^2 \right ] + 1](_images/math/aaa56b020c32543eb520102d36e95cecc0698fdd.png)
That said, my approach to generate test functions for this benchmark has been the following:
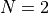 and
and 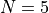
 can be 1, 5, or 10
can be 1, 5, or 10With all these variable settings, I generated 90 valid test function per dimension, thus the current CVMG test suite contains 360 benchmark functions, with dimensionality ranging from 2 to 5.
A few examples of 2D benchmark functions created with the CVMG generator can be seen in Figure 13.1.
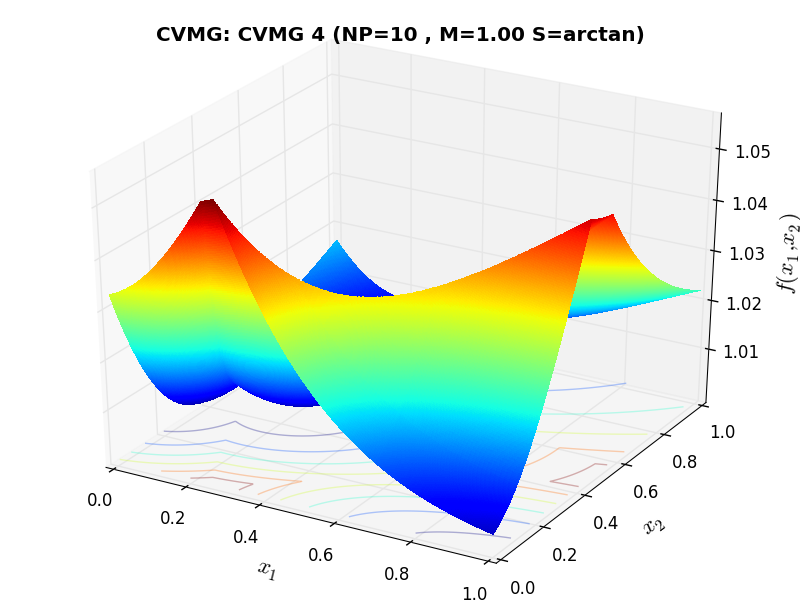
CVMG Function 4 |
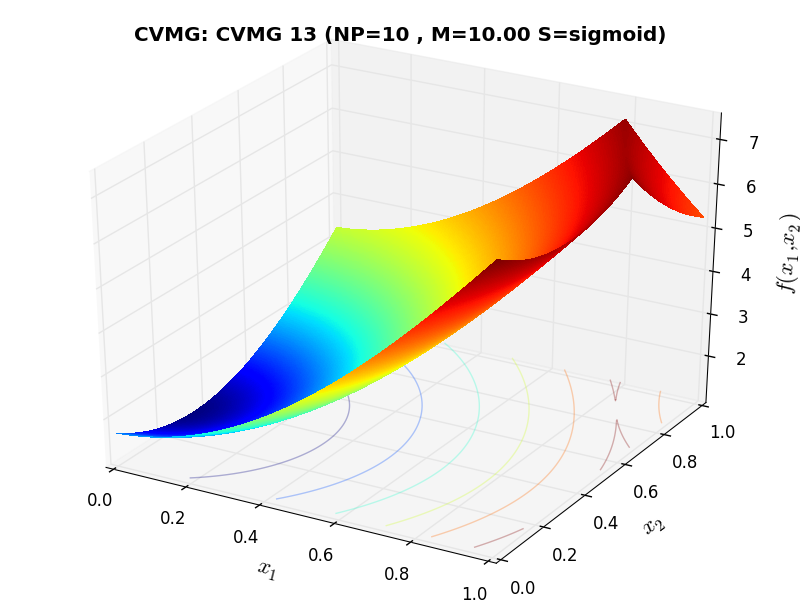
CVMG Function 13 |
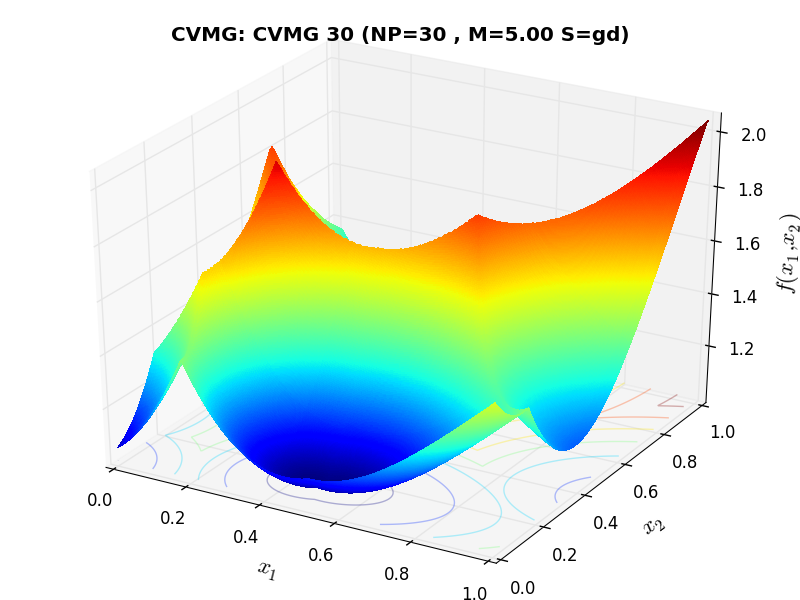
CVMG Function 30 |
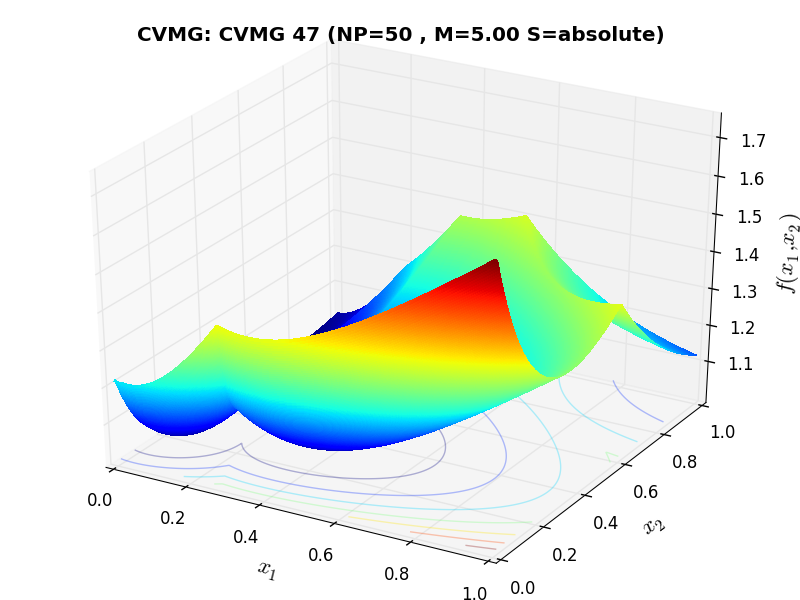
CVMG Function 47 |

CVMG Function 66 |
CVMG Function 86 |
 General Solvers Performances¶
General Solvers Performances¶Table 13.1 below shows the overall success of all Global Optimization algorithms, considering every benchmark function,
for a maximum allowable budget of  .
.
The CVMG benchmark suite is a medium-difficulty test suite: the best solver for  is MCS, with a success
rate of 56.4%, but many solvers are close to that performance: DIRECT, BasinHopping, SHGO, DualAnnealing and AMPGO
all stand between 3% to the top optimization algorithm.
is MCS, with a success
rate of 56.4%, but many solvers are close to that performance: DIRECT, BasinHopping, SHGO, DualAnnealing and AMPGO
all stand between 3% to the top optimization algorithm.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 53.89% | 252 |
| BasinHopping | 55.00% | 155 |
| BiteOpt | 47.22% | 263 |
| CMA-ES | 50.83% | 424 |
| CRS2 | 40.56% | 683 |
| DE | 48.33% | 1,069 |
| DIRECT | 55.56% | 185 |
| DualAnnealing | 54.17% | 119 |
| LeapFrog | 42.50% | 184 |
| MCS | 56.39% | 106 |
| PSWARM | 41.94% | 1,369 |
| SCE | 50.56% | 435 |
| SHGO | 54.72% | 130 |
These results are also depicted in Figure 13.2, which shows that MCS is the better-performing optimization algorithm, followed by very many other solvers with similar performances.
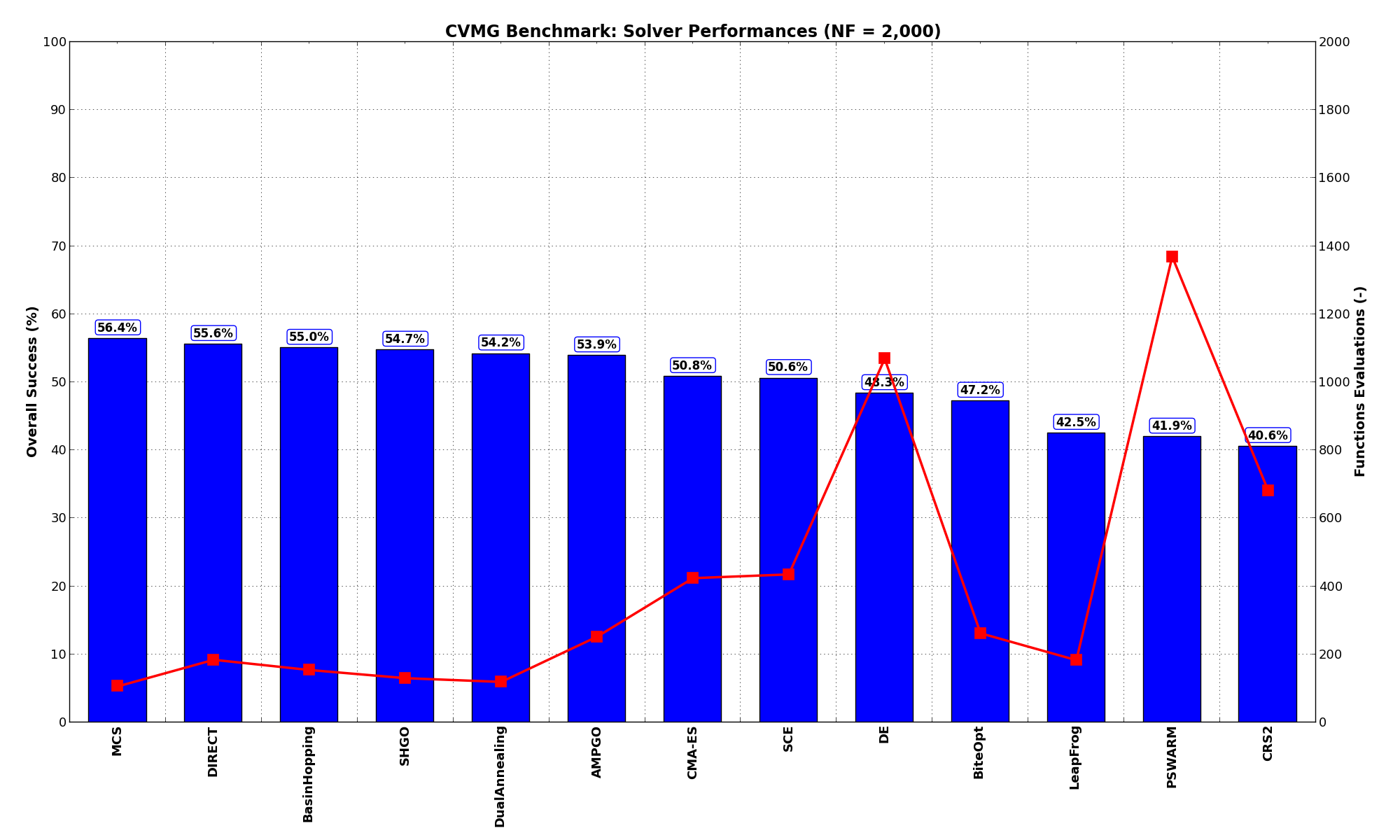
Figure 13.2: Optimization algorithms performances on the CVMG test suite at 
Pushing the available budget to a very generous  , the results show AMPGO snatching the top spot from MCS,
which is anyway very close to it in second place. As before, DIRECT, BasinHopping, SHGO and DualAnnealing
are not that far behind. The results are also shown visually in Figure 13.3.
, the results show AMPGO snatching the top spot from MCS,
which is anyway very close to it in second place. As before, DIRECT, BasinHopping, SHGO and DualAnnealing
are not that far behind. The results are also shown visually in Figure 13.3.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 58.33% | 550 |
| BasinHopping | 55.83% | 199 |
| BiteOpt | 49.17% | 517 |
| CMA-ES | 53.33% | 563 |
| CRS2 | 40.56% | 683 |
| DE | 53.06% | 1,248 |
| DIRECT | 56.11% | 223 |
| DualAnnealing | 54.72% | 149 |
| LeapFrog | 42.50% | 184 |
| MCS | 56.94% | 155 |
| PSWARM | 48.89% | 1,522 |
| SCE | 53.61% | 669 |
| SHGO | 56.11% | 245 |
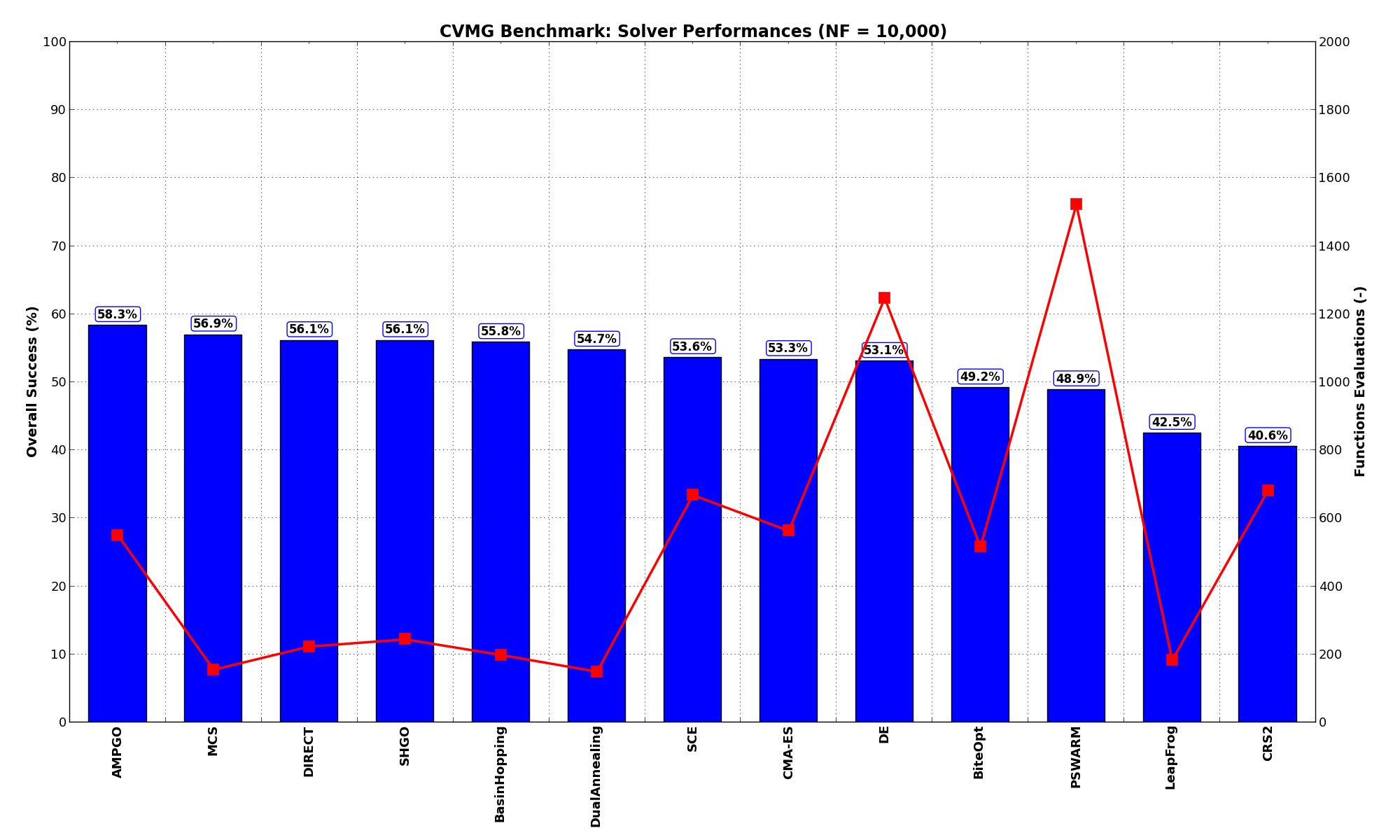
Figure 13.3: Optimization algorithms performances on the CVMG test suite at 
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 13.4.
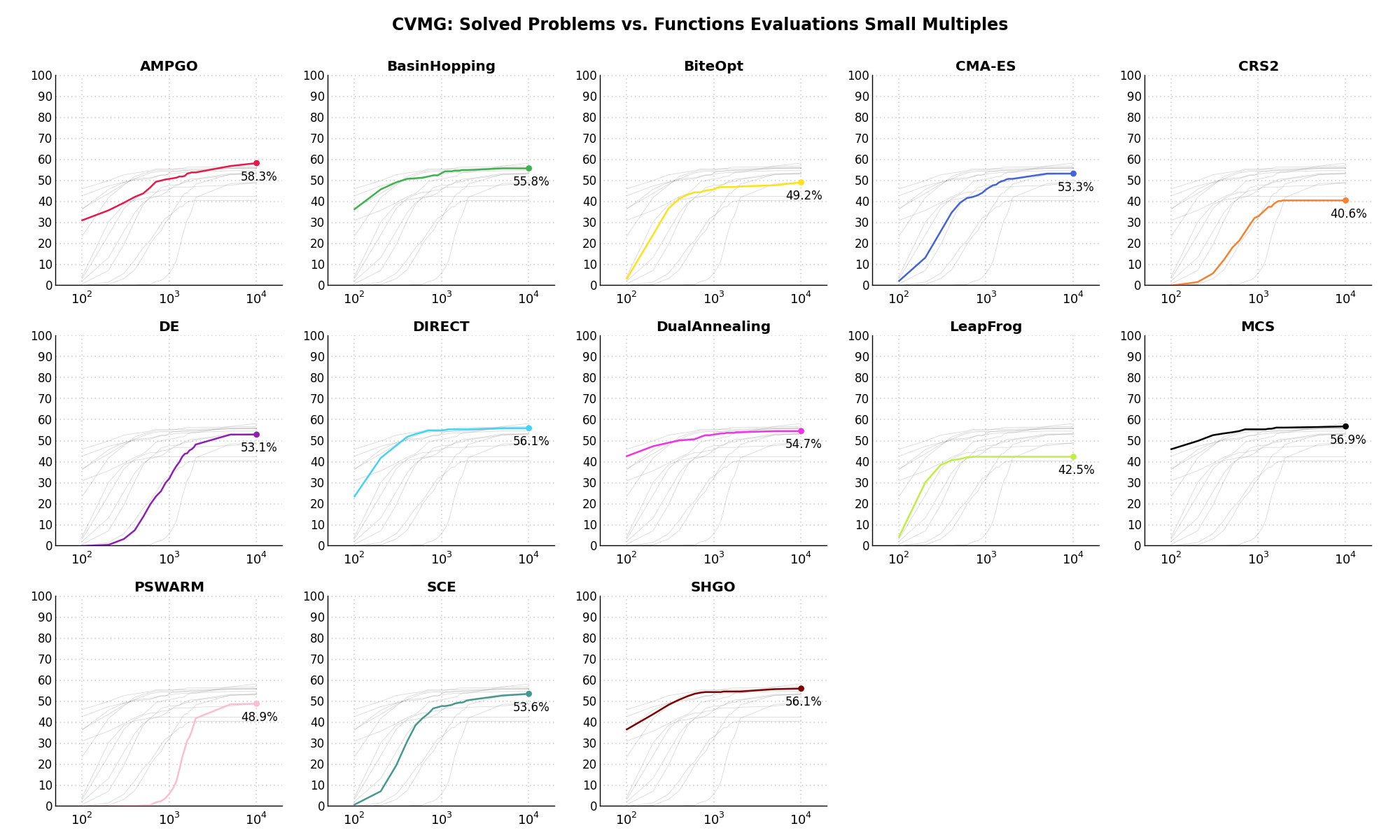
Figure 13.4: Percentage of problems solved given a fixed number of function evaluations on the CVMG test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 13.5 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
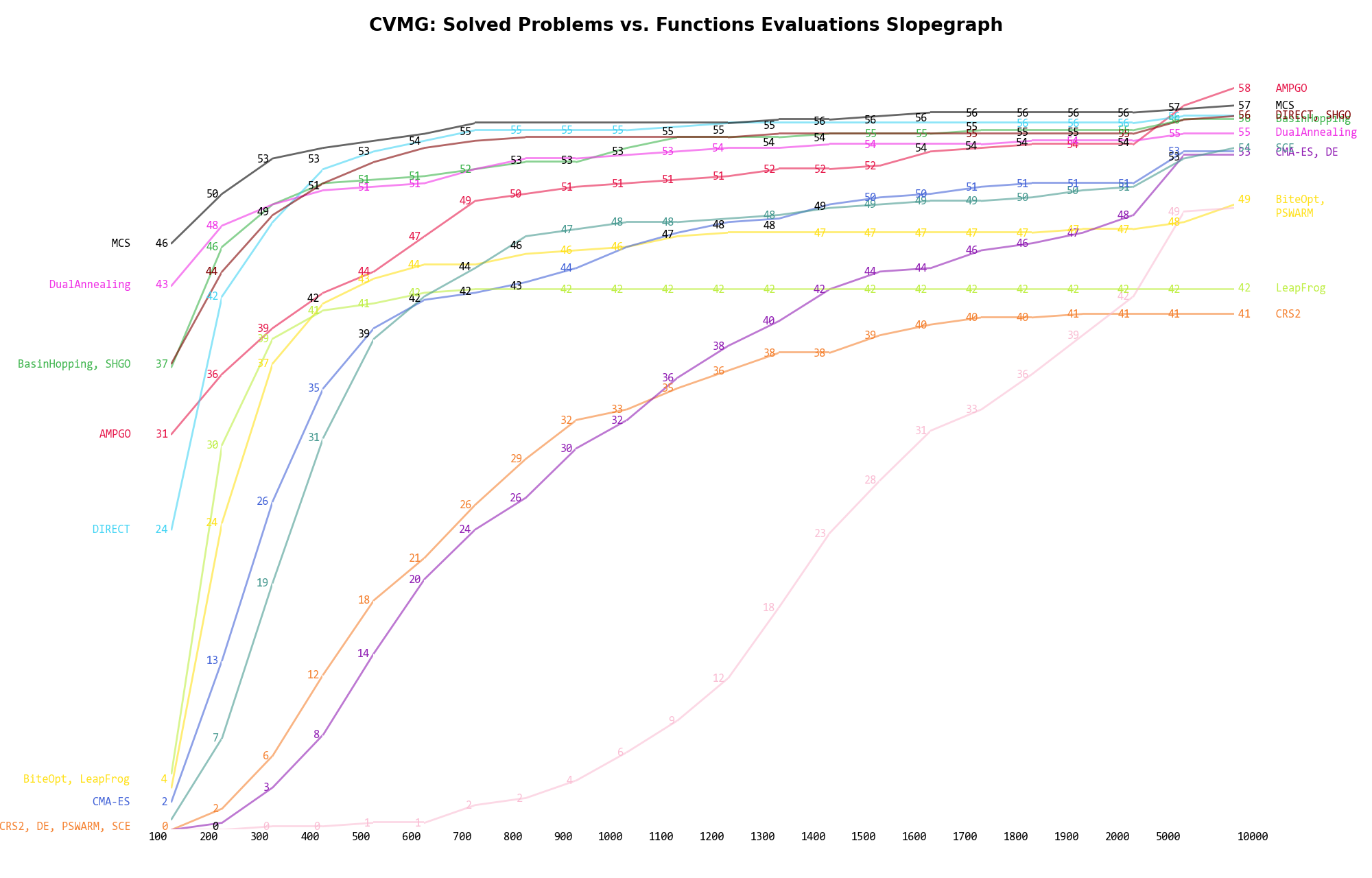
Figure 13.5: Percentage of problems solved given a fixed number of function evaluations on the CVMG test suite
A few obvious conclusions we can draw from these pictures are:
 .
. Dimensionality Effects¶
Dimensionality Effects¶Since I used the CVMG test suite to generate test functions with dimensionality ranging from 2 to 5, it is interesting to take a look at the solvers performances as a function of the problem dimensionality. Of course, in general it is to be expected that for larger dimensions less problems are going to be solved - although it is not always necessarily so as it also depends on the function being generated. Results are shown in Table 13.3 .
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 88.9 | 71.1 | 36.7 | 18.9 | 53.9 |
| BasinHopping | 91.1 | 75.6 | 34.4 | 18.9 | 55.0 |
| BiteOpt | 86.7 | 57.8 | 30.0 | 14.4 | 47.2 |
| CMA-ES | 88.9 | 67.8 | 28.9 | 17.8 | 50.8 |
| CRS2 | 67.8 | 53.3 | 24.4 | 16.7 | 40.6 |
| DE | 88.9 | 73.3 | 28.9 | 2.2 | 48.3 |
| DIRECT | 91.1 | 76.7 | 36.7 | 17.8 | 55.6 |
| DualAnnealing | 91.1 | 72.2 | 34.4 | 18.9 | 54.2 |
| LeapFrog | 75.6 | 58.9 | 23.3 | 12.2 | 42.5 |
| MCS | 91.1 | 77.8 | 36.7 | 20.0 | 56.4 |
| PSWARM | 84.4 | 58.9 | 15.6 | 8.9 | 41.9 |
| SCE | 76.7 | 71.1 | 35.6 | 18.9 | 50.6 |
| SHGO | 91.1 | 76.7 | 36.7 | 14.4 | 54.7 |
Figure 13.6 shows the same results in a visual way.
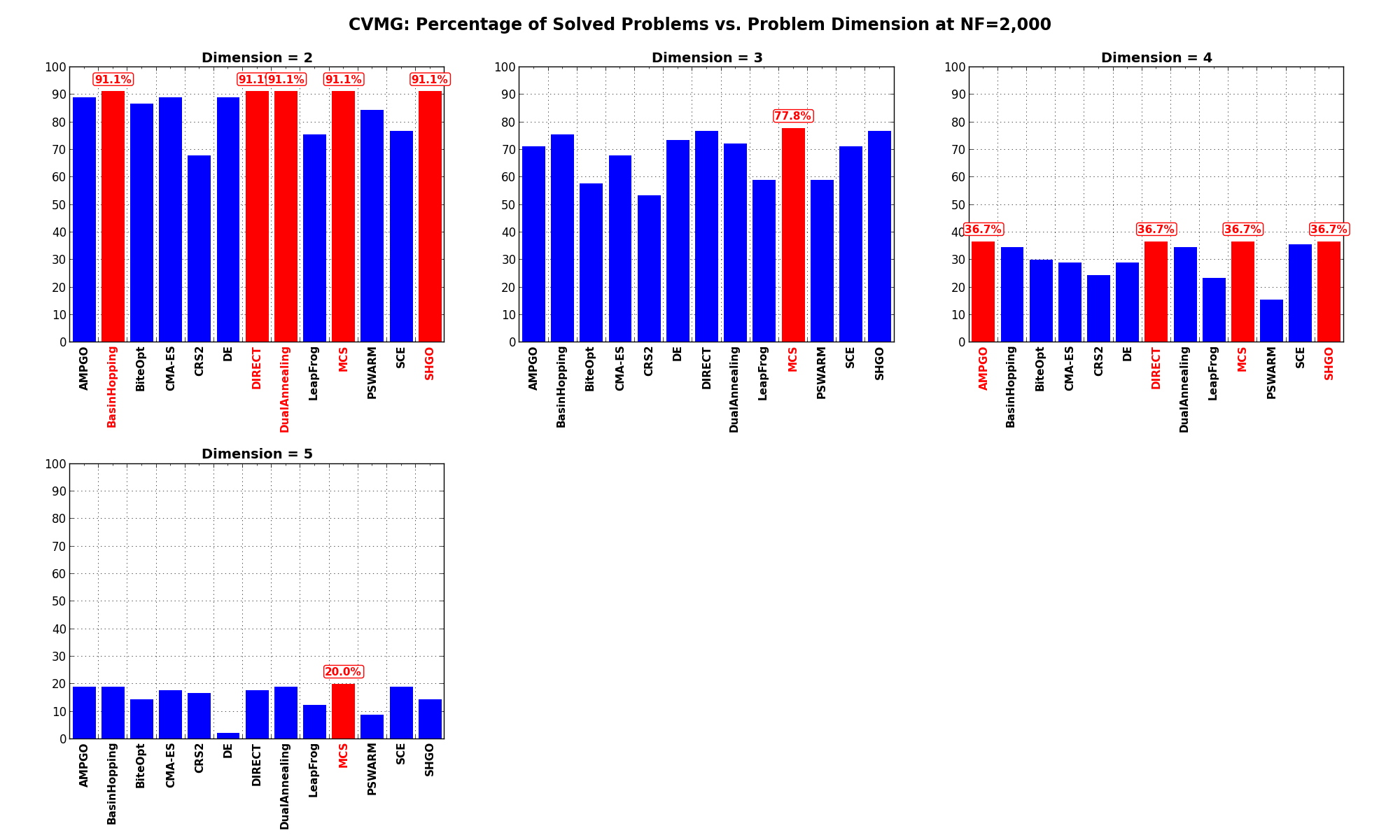
Figure 13.6: Percentage of problems solved as a function of problem dimension for the CVMG test suite at 
What we can infer from the table and the figure is that, for low dimensionality problems (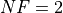 ), very many solvers
are able to solve most of the problems in this test suite, with MCS, DIRECT, BasinHopping, SHGO and DualAnnealing leading the pack.
By increasing the dimensionality those solvers stay close to one another but of course the percentage of solved problems
decrease dramatically.
), very many solvers
are able to solve most of the problems in this test suite, with MCS, DIRECT, BasinHopping, SHGO and DualAnnealing leading the pack.
By increasing the dimensionality those solvers stay close to one another but of course the percentage of solved problems
decrease dramatically.
Pushing the available budget to a very generous  shows AMPGO taking the lead for higher dimensional
problems (
shows AMPGO taking the lead for higher dimensional
problems ( ), finally coming up as the winner for this benchmark test suite.
), finally coming up as the winner for this benchmark test suite.
The results for the benchmarks at  are displayed in Table 13.4 and Figure 13.7.
are displayed in Table 13.4 and Figure 13.7.
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 91.1 | 77.8 | 41.1 | 23.3 | 58.3 |
| BasinHopping | 91.1 | 75.6 | 36.7 | 20.0 | 55.8 |
| BiteOpt | 88.9 | 63.3 | 30.0 | 14.4 | 49.2 |
| CMA-ES | 90.0 | 70.0 | 33.3 | 20.0 | 53.3 |
| CRS2 | 67.8 | 53.3 | 24.4 | 16.7 | 40.6 |
| DE | 88.9 | 73.3 | 31.1 | 18.9 | 53.1 |
| DIRECT | 91.1 | 76.7 | 36.7 | 20.0 | 56.1 |
| DualAnnealing | 91.1 | 74.4 | 34.4 | 18.9 | 54.7 |
| LeapFrog | 75.6 | 58.9 | 23.3 | 12.2 | 42.5 |
| MCS | 91.1 | 77.8 | 37.8 | 21.1 | 56.9 |
| PSWARM | 85.6 | 64.4 | 26.7 | 18.9 | 48.9 |
| SCE | 87.8 | 71.1 | 35.6 | 20.0 | 53.6 |
| SHGO | 91.1 | 76.7 | 36.7 | 20.0 | 56.1 |
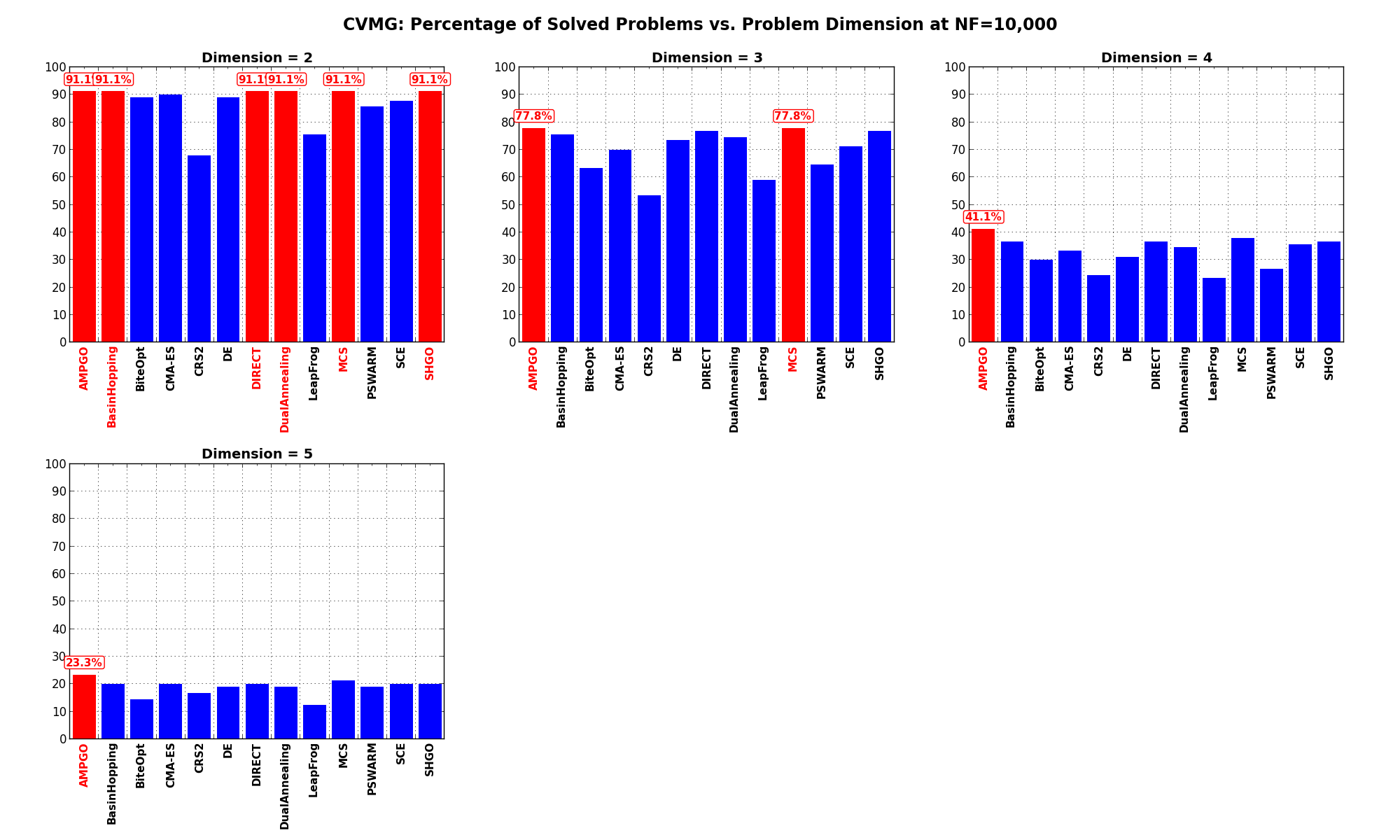
Figure 13.7: Percentage of problems solved as a function of problem dimension for the CVMG test suite at 