Navigation
- index
- next |
- previous |
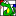
- Home »
- The Benchmarks »
- MMTFG
 MMTFG¶
MMTFG¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| Yes | Yes | Easy |
The MMTFG test function generator of global optimization test functions is almost as famous as the GKLS one. It is described in the paper A framework for generating tunable test functions for multimodal optimization. I have taken the original C code (available at http://www.ronkkonen.com/generator/ ), and I have instructed the benchmark runner (that is written in Python) to communicate with the C driver via input files - the default for the MMTFG generator, as my Cython skills were not good enough to wrap the code as it is.
The acronym MMTFG obviously stands for Multi-Modal Test Function Generator, as the article above describes it.
Even though there are no code conversions involved, I still like to check that things add up correctly while using a test
functions generator. I then have compared the results of the original C code and of my bridge to it ad they are exactly the same: this is easy to see by comparing
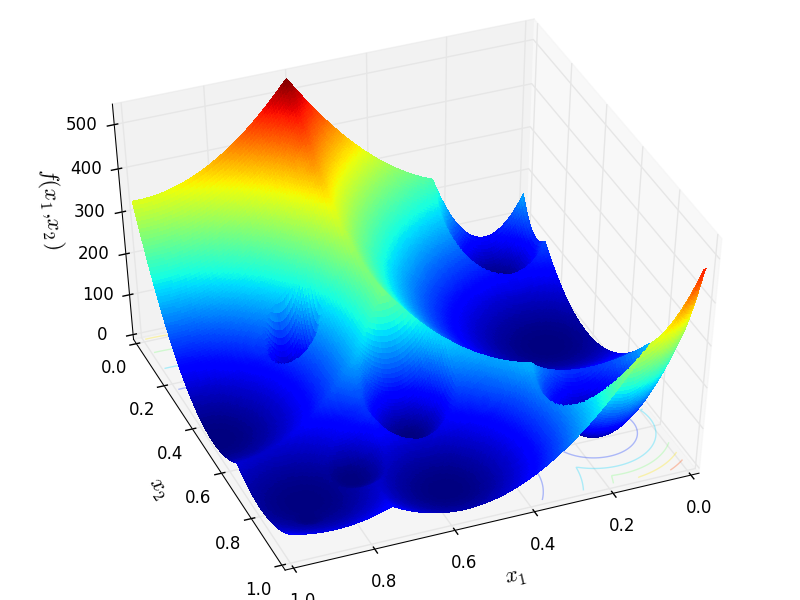
Figure 2 (a) and Figure 2 (b) in the paper above with Figure 4.1 below. Thr first picture shows a MMTFG quadratic family
function from a two-dimensional test functions with 10 spherical, global minima. The second figure has 10 global and 100 local
rotated ellipsoidal minima such that the local minima points have fitness value in range ![[-0.95,-0.15]](_images/math/d0428c6cfad2d9b08da39976bf56b5618fecb477.png) .
Globally optimal value is always -1.
.
Globally optimal value is always -1.
MMTFG Function 1
MMTFG Function 2
 Methodology¶
Methodology¶The MMTFG generator can be used to generate multimodal test functions for minimization, tunable with parameters to allow generation of landscape characteristics that are specifically designed for evaluating multimodal optimization algorithms by their ability to locate multiple optima. At the moment, three families of functions exist, but the generator is easily expandable and new families may be added in future. The current families are cosine, quadratic and common families.
The cosine family samples two cosine curves together, of which one defines global minima and another adds local minima. The basic internal structure is regular: all minima are of similar size and shape and located in rows of similar distance from each other. The function family is defined by:
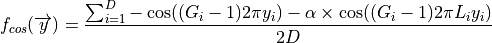
where ![\overrightarrow{y} \in [0, 1]^D](_images/math/f9ffcfe769f345b881066e6f3f52e26b81d32e42.png) ,
, 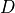 is the dimensionality, the parameters
is the dimensionality, the parameters 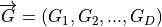 and
and  are vectors of positive integers which define the number of global and
local minima for each dimension, and
are vectors of positive integers which define the number of global and
local minima for each dimension, and ![\alpha \in (0, 1]](_images/math/87227ce0e71a0e317bfcf0b7ce695a58aba55b25.png) defines the amplitude of the sampling function (depth of the local
minima). The generator allows the function to be rotated to a random angle and use Bezier curves to stretch
each dimension independently to decrease the regularity.
defines the amplitude of the sampling function (depth of the local
minima). The generator allows the function to be rotated to a random angle and use Bezier curves to stretch
each dimension independently to decrease the regularity.
The quadratic family can be used to generate completely irregular landscapes. The function is created by combining several
minima generated independently. They are described as a 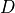 dimensional general quadratic form, where a symmetric
matrix
dimensional general quadratic form, where a symmetric
matrix 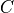 defines the shape of each minimum. The functions in quadratic family need not be stretched or rotated,
because no additional benefit would be gained by doing that to an already irregular function. However, axis-aligned minima
may be randomly rotated by rotating the matrix
defines the shape of each minimum. The functions in quadratic family need not be stretched or rotated,
because no additional benefit would be gained by doing that to an already irregular function. However, axis-aligned minima
may be randomly rotated by rotating the matrix 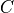 with a matrix
with a matrix ![\mathbf{O} = [\mathbf{\overrightarrow{o_1}}, ..., \mathbf{\overrightarrow{o_D}}]](_images/math/54a919e782776c561c579cf00d998e5e3290b911.png) is a randomly generated angle preserving orthogonal linear transformation such as:
is a randomly generated angle preserving orthogonal linear transformation such as:
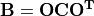
The functions in the quadratic family are then calculated by:
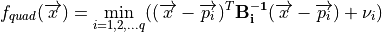
where ![\overrightarrow{x} \in [0, 1]^D](_images/math/c30e760fead0f59b686460f117baa9d3195f4e64.png) ,
, 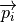 defines the location and
defines the location and 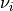 the fitness
value of a minimum point for the i’th minimum.
the fitness
value of a minimum point for the i’th minimum. 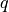 is the number of minima.
is the number of minima.
The hump family implements the generic hump functions family proposed by Singh and Deb (2006). Like the quadratic family, the hump functions allow irregular landscapes to be generated and the number of minima to be defined independently of the dimensionality. The placement of minima is chosen randomly. Each minimum is defined by:
![f_{hump}(\overrightarrow{y}) = \begin{cases}
h_i\left[1 - \left ( \frac{d(\overrightarrow{y}, i)}{r_i} \right )^{\alpha_i} \right ], & \textrm{ if } d(\overrightarrow{y}, i) \leq r_i \\
0, & \textrm{ otherwise }
\end{cases}](_images/math/2adc766511cdbe805928be9fe9c381bc3d8ff24e.png)
where ![\overrightarrow{y} \in [0, 1]^D](_images/math/f9ffcfe769f345b881066e6f3f52e26b81d32e42.png) ,
, 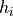 is the value of the i th minimum,
is the value of the i th minimum, 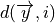 is the Euclidean distance between
is the Euclidean distance between  and the center of the i th minimum,
and the center of the i th minimum, 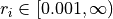 defines the basin radius and
defines the basin radius and ![\alpha \in [0.001, 1]](_images/math/a348be692d2603acb7bb4a3b262c7fc41b717d90.png) the shape of the i th minimum slope.
the shape of the i th minimum slope.
My approach in building the test functions using the MMTFG generator has been family dependent, and in particular:
For all families, the number of dimensions ranges from 2 to 4
Armed with all these combinations - and please keep in mind that some combinations, especially in the quadratic family, are invalid due to internal constraints in the test function generator - I have generated a total of 981 benchmark functions divided as presented in Table 4.1:
| Family | N = 2 | N = 3 | N = 4 | Total |
|---|---|---|---|---|
| Cos | 108 | 108 | 108 | 324 |
| Hump | 96 | 96 | 96 | 288 |
| Quad | 108 | 126 | 135 | 369 |
| Total | 312 | 330 | 339 | 981 |
A few examples of 2D benchmark functions created with the MMTFG generator can be seen in Figure 4.2.
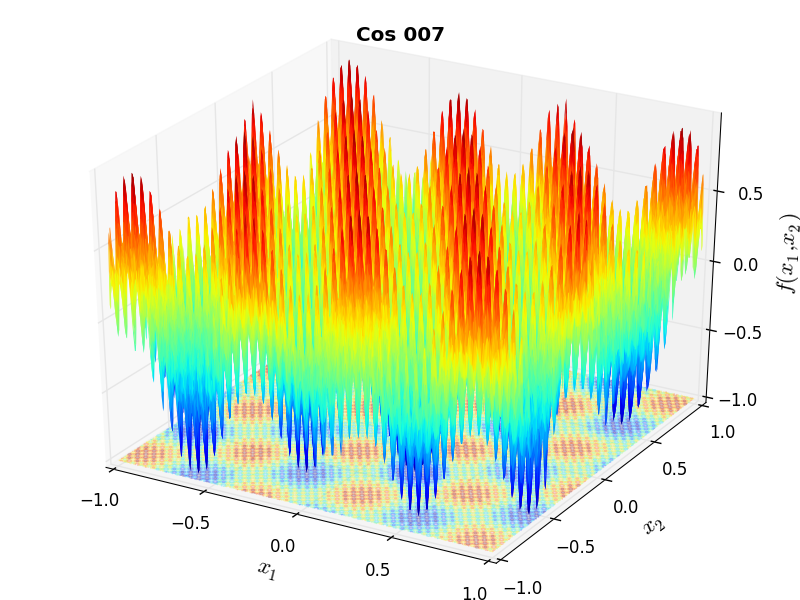
MMTFG Cosine 7 |
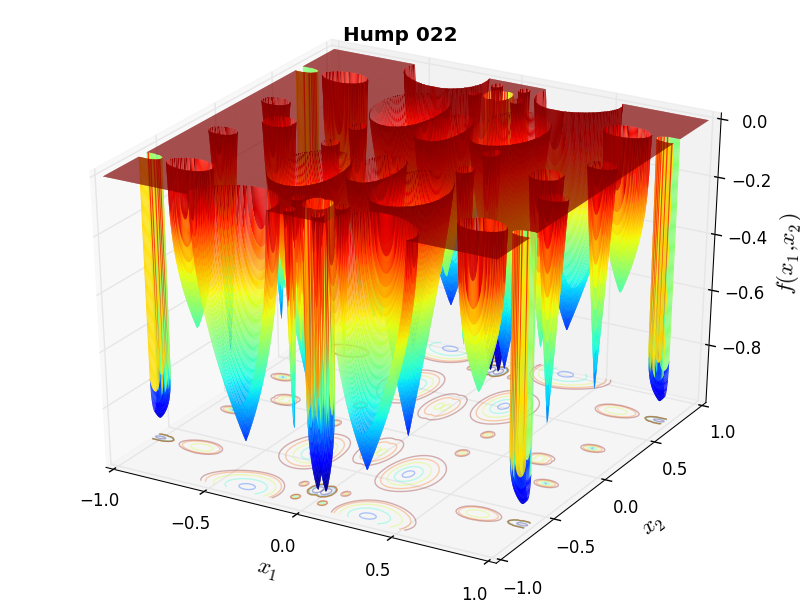
MMTFG Hump 22 |
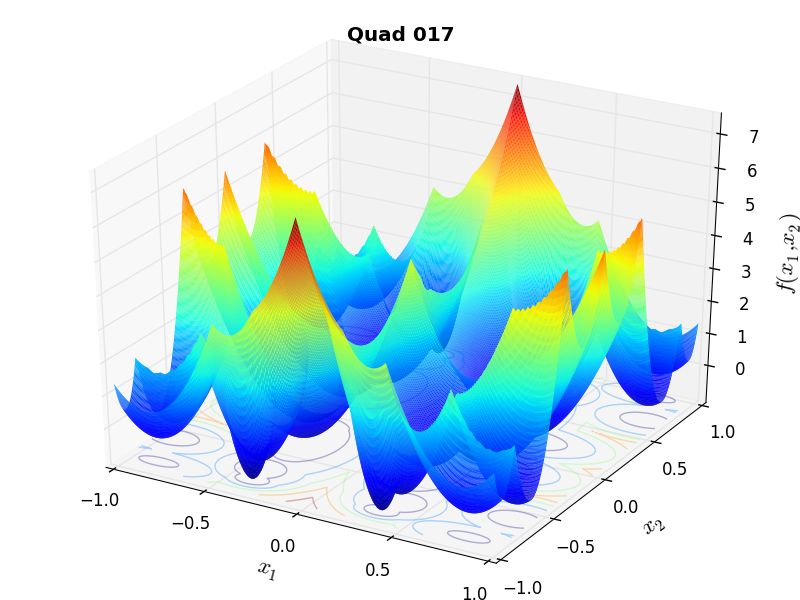
MMTFG Quad 17 |
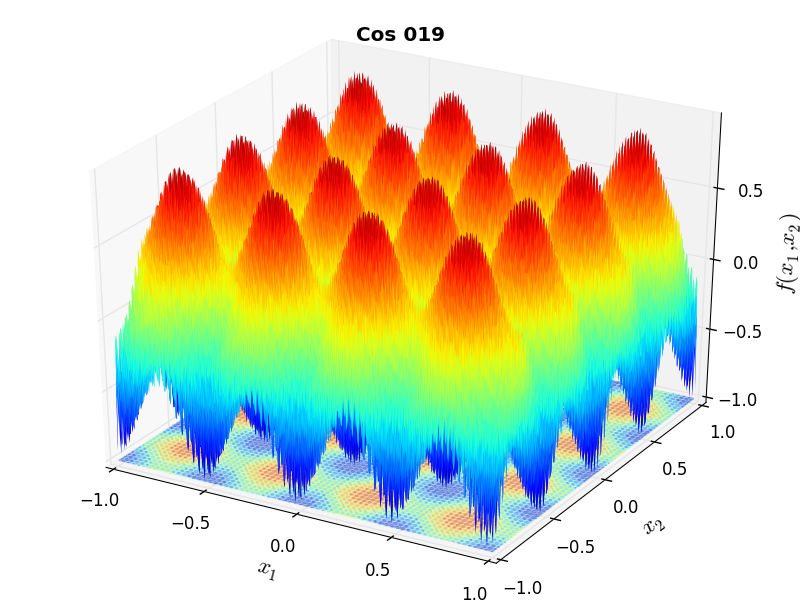
MMTFG Cosine 19 |
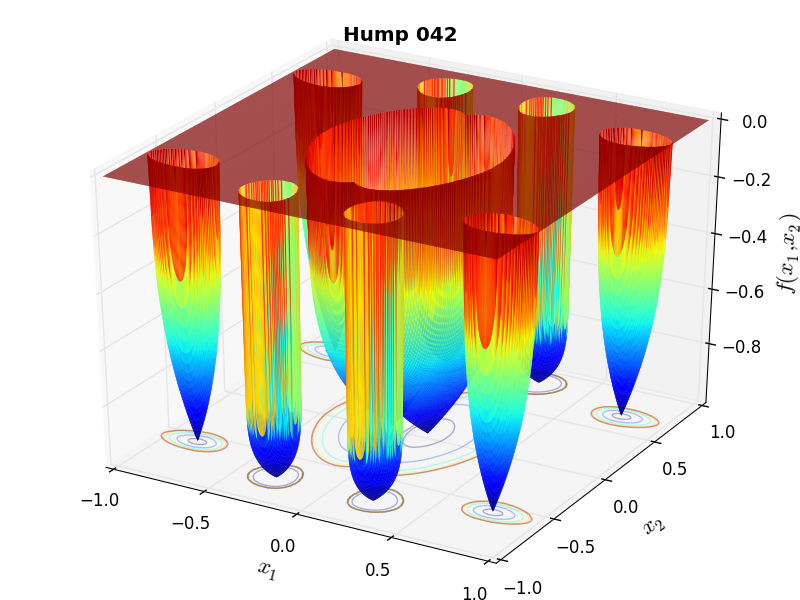
MMTFG Hump 42 |
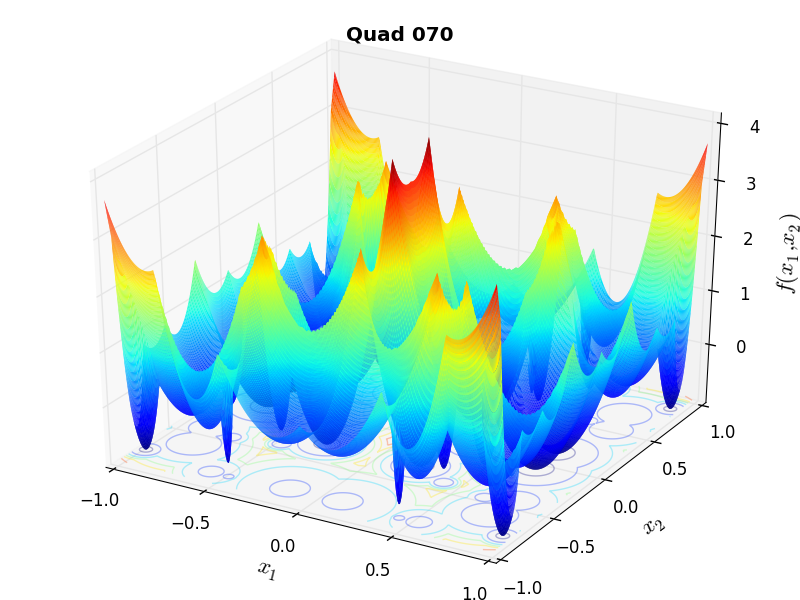
MMTFG Quad 70 |
 General Solvers Performances¶
General Solvers Performances¶Table 4.2 below shows the overall success of all Global Optimization algorithms, considering every benchmark function,
for a maximum allowable budget of  .
.
As we can see - and in contrast with the GKLS and GlobOpt test function generators - the level of difficulty of the MMTFG test suite is much lower, as the best solver ( MCS) solves up to 77% of all the problems with less than 300 function evaluations. Second comes the BiteOpt algorithm, but many of the SciPy solvers are up there too - BasinHopping, DualAnnealing and SHGO provide excellent performances on this test suite.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 60.24% | 461 |
| BasinHopping | 72.07% | 319 |
| BiteOpt | 72.27% | 515 |
| CMA-ES | 52.19% | 570 |
| CRS2 | 49.85% | 1,007 |
| DE | 32.93% | 1,396 |
| DIRECT | 59.43% | 419 |
| DualAnnealing | 66.97% | 313 |
| LeapFrog | 43.93% | 278 |
| MCS | 77.06% | 287 |
| PSWARM | 19.57% | 890 |
| SCE | 24.57% | 958 |
| SHGO | 69.22% | 295 |
These results are also depicted in Figure 4.3, which shows that MCS is the better-performing optimization algorithm, followed by BiteOpt and BasinHopping.
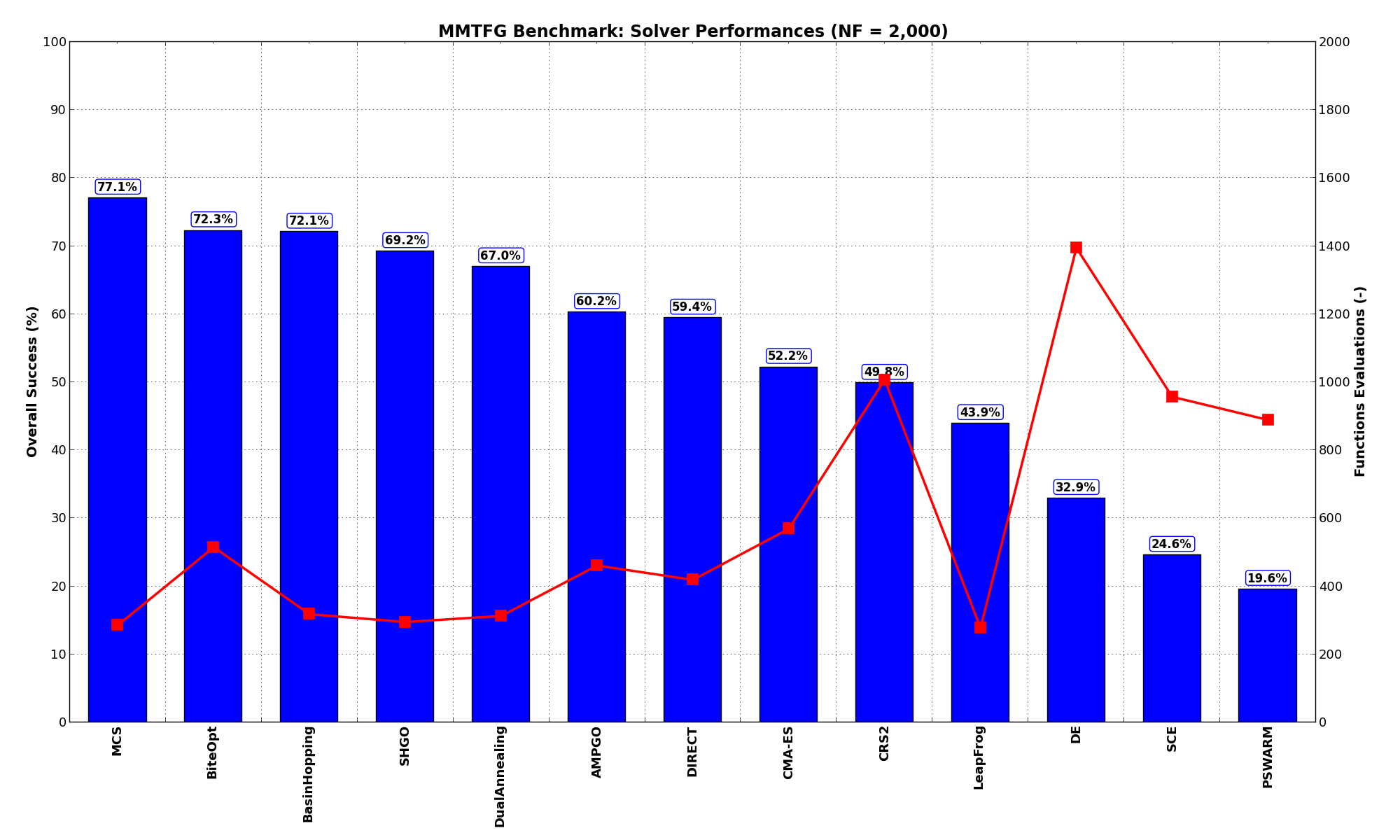
Figure 4.3: Optimization algorithms performances on the MMTFG test suite at 
Pushing the available budget to a very generous  , the results show MCS taking the lead
on other solvers (about 6% more problems solved compared to the second best, BiteOpt). The results are also
shown visually in Figure 4.4.
, the results show MCS taking the lead
on other solvers (about 6% more problems solved compared to the second best, BiteOpt). The results are also
shown visually in Figure 4.4.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 75.84% | 1,359 |
| BasinHopping | 77.68% | 518 |
| BiteOpt | 78.90% | 887 |
| CMA-ES | 66.77% | 1,449 |
| CRS2 | 61.06% | 1,422 |
| DE | 71.97% | 2,880 |
| DIRECT | 64.42% | 746 |
| DualAnnealing | 71.25% | 473 |
| LeapFrog | 43.93% | 278 |
| MCS | 85.52% | 726 |
| PSWARM | 67.69% | 2,454 |
| SCE | 35.47% | 2,018 |
| SHGO | 78.70% | 679 |
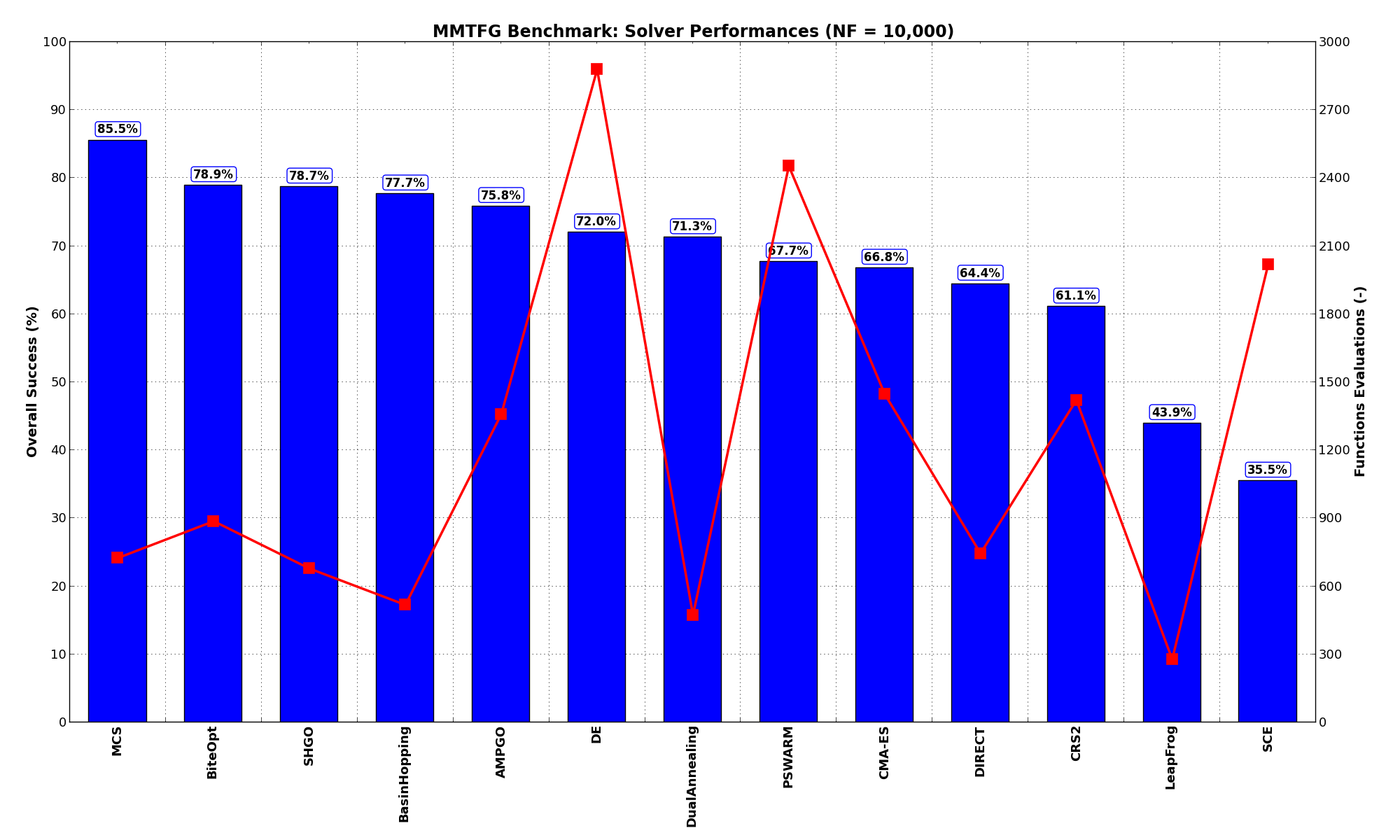
Figure 4.4: Optimization algorithms performances on the MMTFG test suite at 
All the solvers except for LeapFrog and SCE are able to solve more than 60% of the problems if given a generous
budget as we did above at  .
.
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 4.5.
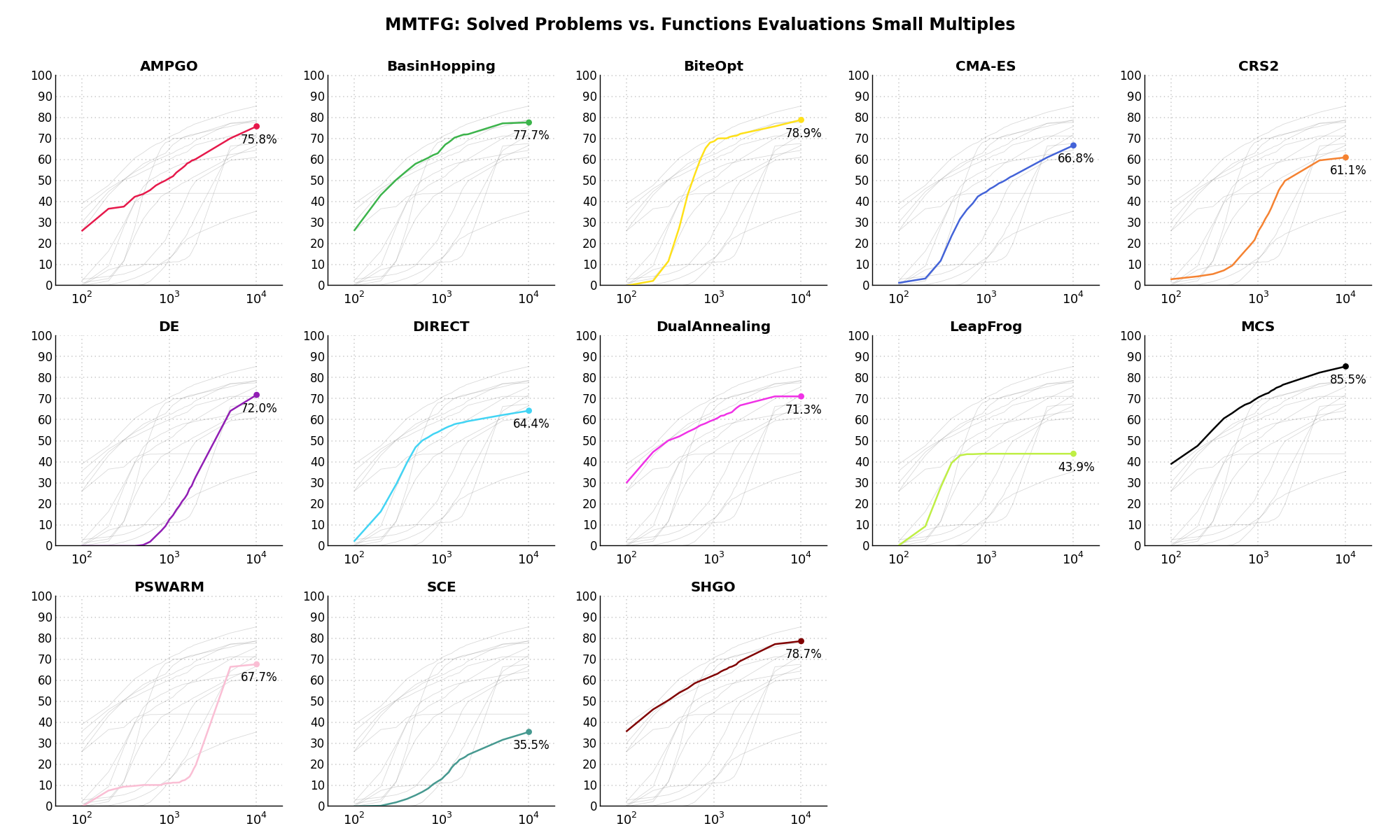
Figure 4.5: Percentage of problems solved given a fixed number of function evaluations on the MMTFG test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 4.6 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
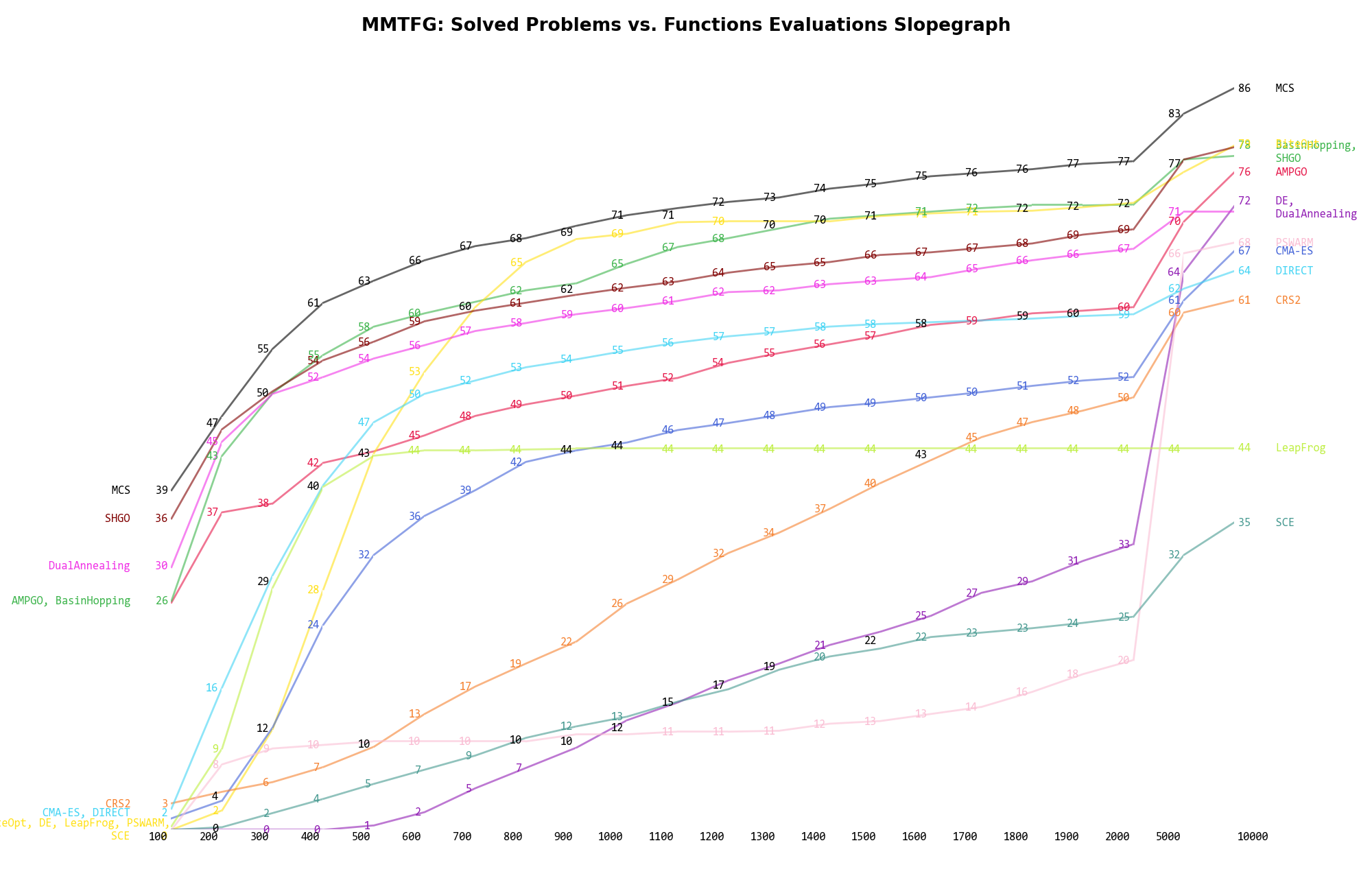
Figure 4.6: Percentage of problems solved given a fixed number of function evaluations on the MMTFG test suite
A few obvious conclusions we can draw from these pictures are:
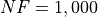 function evaluations.....
function evaluations..... and
and  ,
and a very similar argument can be made for DE.
,
and a very similar argument can be made for DE. Dimensionality Effects¶
Dimensionality Effects¶Since I used the MMTFG test suite to generate test functions with dimensionality ranging from 2 to 4, it is interesting to take a look at the solvers performances as a function of the problem dimensionality. Of course, in general it is to be expected that for larger dimensions less problems are going to be solved - although it is not always necessarily so as it also depends on the function being generated. Results are shown in Table 4.4 .
| Solver | N = 2 | N = 3 | N = 4 | Overall |
|---|---|---|---|---|
| AMPGO | 76.9 | 63.6 | 41.6 | 60.7 |
| BasinHopping | 83.3 | 71.2 | 62.5 | 72.4 |
| BiteOpt | 84.6 | 71.5 | 61.7 | 72.6 |
| CMA-ES | 68.9 | 50.0 | 38.9 | 52.6 |
| CRS2 | 74.4 | 50.6 | 26.5 | 50.5 |
| DE | 77.9 | 24.2 | 0.0 | 34.0 |
| DIRECT | 78.2 | 58.2 | 43.4 | 59.9 |
| DualAnnealing | 86.9 | 61.5 | 54.0 | 67.5 |
| LeapFrog | 57.7 | 46.4 | 28.9 | 44.3 |
| MCS | 92.6 | 76.1 | 63.7 | 77.5 |
| PSWARM | 33.7 | 10.6 | 15.3 | 19.9 |
| SCE | 39.1 | 18.8 | 16.8 | 24.9 |
| SHGO | 88.8 | 68.5 | 51.9 | 69.7 |
Figure 4.7 shows the same results in a visual way.
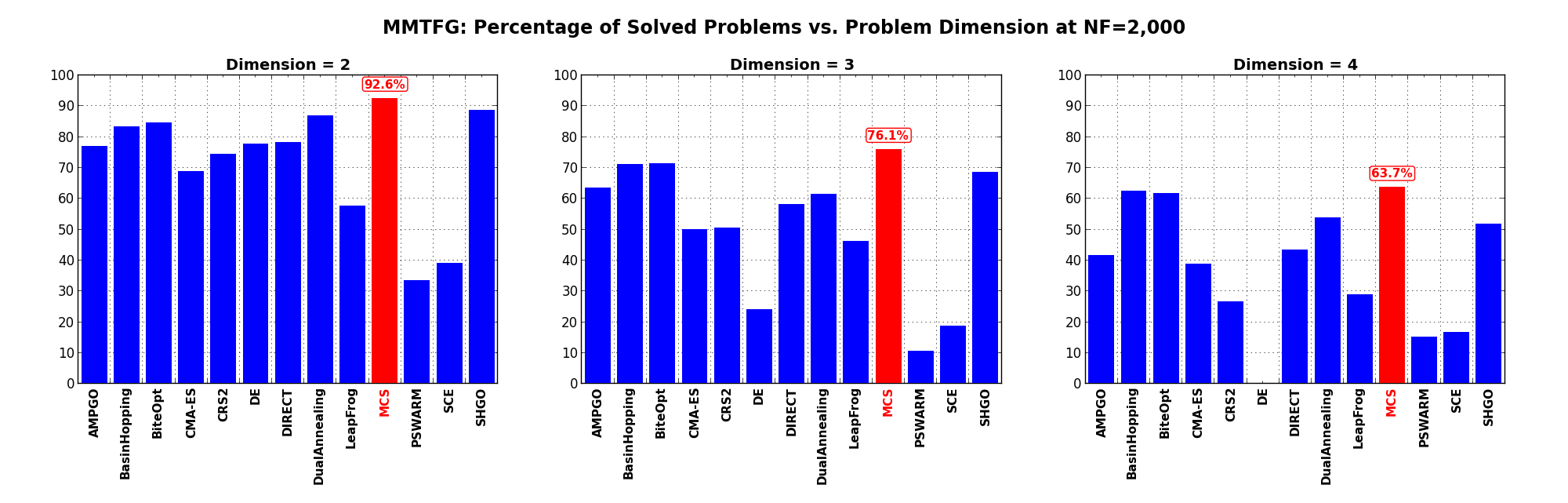
Figure 4.7: Percentage of problems solved as a function of problem dimension for the MMTFG test suite at 
What we can infer from the table and the figure is that, for lower dimensionality problems (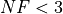 ), MCS,
SHGO, BasinHopping and BiteOpt solve the vast majority of problems (90%). For higher dimensionality problems (
), MCS,
SHGO, BasinHopping and BiteOpt solve the vast majority of problems (90%). For higher dimensionality problems (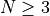 ), all
those solvers keep a very good performance, although it is to be expected that the number of problems solved
decreases with
), all
those solvers keep a very good performance, although it is to be expected that the number of problems solved
decreases with 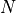 . A dramatic drop in ability to find global optima can be seen for the DE algorithm,
which crashes from 78% success rate at
. A dramatic drop in ability to find global optima can be seen for the DE algorithm,
which crashes from 78% success rate at 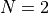 to 0% success for
to 0% success for 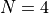 .
.
Pushing the available budget to a very generous  , the results show MCS solving in essence all
the problems at low dimensionality (
, the results show MCS solving in essence all
the problems at low dimensionality (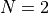 ), closely followed by SHGO, BasinHopping and BiteOpt with more
than 90% of global minima found. For the highest dimensionality in this test suite (
), closely followed by SHGO, BasinHopping and BiteOpt with more
than 90% of global minima found. For the highest dimensionality in this test suite (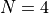 ), we can
of course observe the resurgence of DE which goes up to 55% success rate.
), we can
of course observe the resurgence of DE which goes up to 55% success rate.
The results for the benchmarks at  are displayed in Table 4.5 and Figure 4.8.
are displayed in Table 4.5 and Figure 4.8.
| Solver | N = 2 | N = 3 | N = 4 | Overall |
|---|---|---|---|---|
| AMPGO | 93.3 | 74.8 | 60.8 | 76.3 |
| BasinHopping | 90.4 | 75.8 | 67.8 | 78.0 |
| BiteOpt | 92.3 | 77.6 | 67.8 | 79.2 |
| CMA-ES | 78.8 | 68.5 | 54.0 | 67.1 |
| CRS2 | 75.0 | 61.5 | 47.8 | 61.4 |
| DE | 87.5 | 74.2 | 55.5 | 72.4 |
| DIRECT | 87.2 | 59.7 | 48.1 | 65.0 |
| DualAnnealing | 89.7 | 66.1 | 59.3 | 71.7 |
| LeapFrog | 57.7 | 46.4 | 28.9 | 44.3 |
| MCS | 98.7 | 85.5 | 73.5 | 85.9 |
| PSWARM | 83.3 | 62.1 | 58.7 | 68.1 |
| SCE | 48.1 | 30.0 | 29.2 | 35.8 |
| SHGO | 95.5 | 81.2 | 60.8 | 79.2 |
Figure 4.8 shows the same results in a visual way.
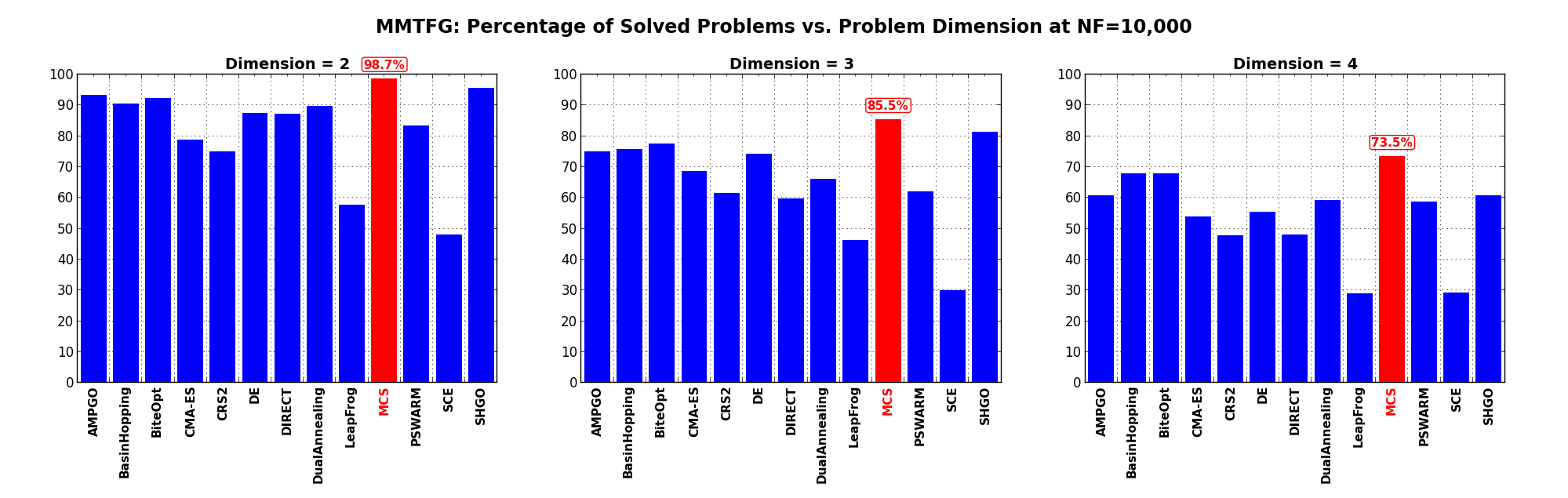
Figure 4.8: Percentage of problems solved as a function of problem dimension for the MMTFG test suite at 
 Family Issues¶
Family Issues¶For this specific test suite, it is interesting to see if any particular family of functions is easier or harder to
solve compared to the others, across all optimization algorithms. This type of results is shown in Table 4.6 and
Table 4.7 below, for  and
and  maximum budget of function evaluations respectively.
maximum budget of function evaluations respectively.
|
|
What seems clear from this tables is that, no matter whether our budget is relatively limited at  or
very generous at
or
very generous at  , the Cosine family appears to be the toughest set to crack, while the Quadratic
family is generally much easier to solve, for almost all the global optimization algorithms considered.
, the Cosine family appears to be the toughest set to crack, while the Quadratic
family is generally much easier to solve, for almost all the global optimization algorithms considered.
This can also be seen in the heatmap presented in Figure 4.9.
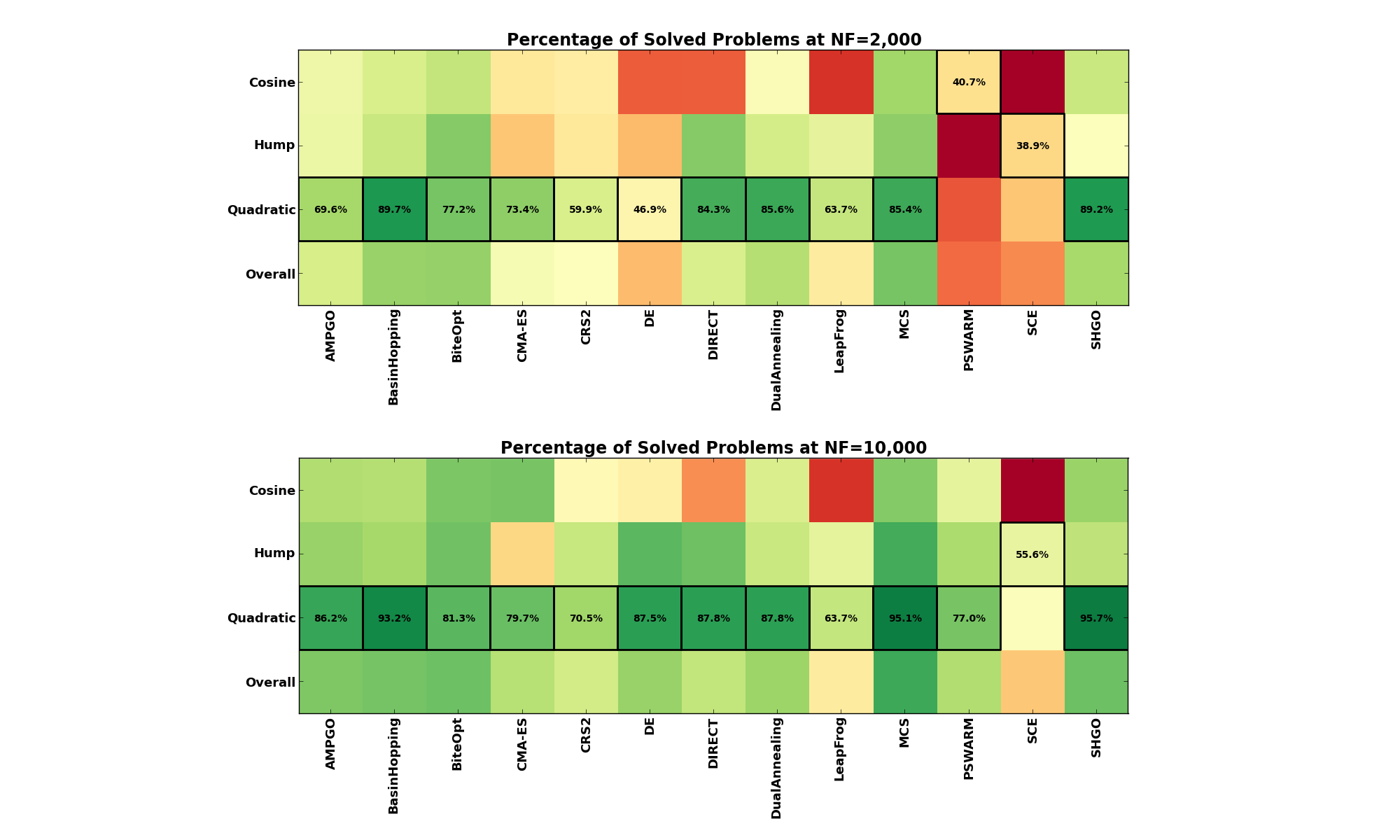
Figure 4.9: Family effects on the MMTFG benchmark suite at  and
and 