Navigation
- index
- next |
- previous |
- Home »
- The Benchmarks »
- GlobOpt
 GlobOpt¶
GlobOpt¶| Fopt Known | Xopt Known | Difficulty |
|---|---|---|
| Yes | No | Hard |
The GlobOpt generator is a benchmark generator for bound-constrained global optimization test functions compared to GKLS. It is described in the paper A new class of test functions for global optimization. “GlobOpt” is not the real name of the generator, I simply used it as the original paper didn’t have a shorter acronym.
Many thanks go to Professor Marco Locatelli for providing an updated copy of the C++ source code. I have taken the original C++ code and wrapped it with Cython in order to link it to the benchmark runner.
I have compared the results of the original C++ code and the ones due to my wrapping and they are exactly the same: this is easy to see by comparing Figure 3 in the paper above with Figure 3.1 below.
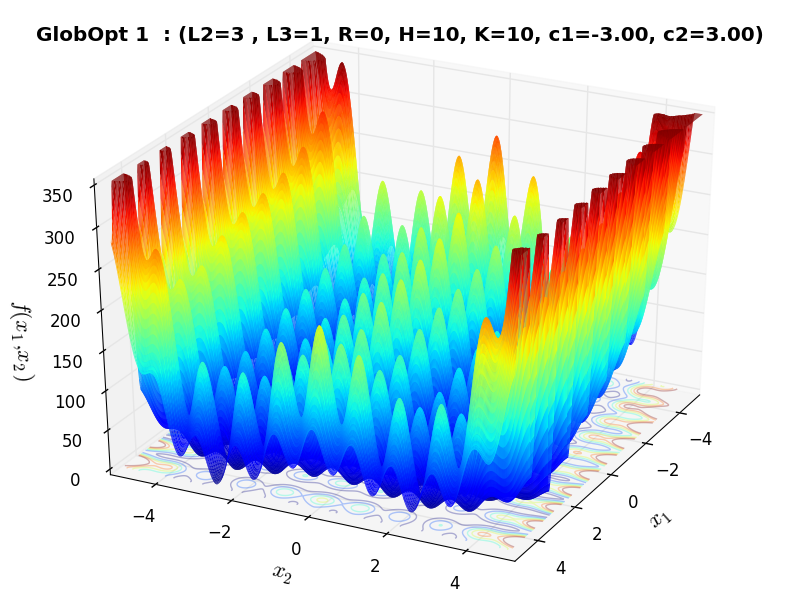
Figure 3.1: A two-dimensional GlobOpt function with 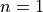 ,
, 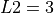 ,
, 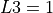 ,
, 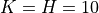 over the box
over the box ![[−5, 5]^2](_images/math/0b7b74f911cf2cc83218261a7b32b2f3590a69cb.png)
 Methodology¶
Methodology¶The derivation of the test functions in the GlobOpt benchmark suite is kind of complicated to describe in a short section,
but I wll do my best to summarize my understanding of the original paper. The method uses functions composition to create
highly multimodal, difficult to minimize test functions. The idea behind the GlobOpt generator is that local minima can
be classified in “levels” - in terms of levels of difficulty. Level 1 minima (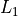 ) are the easy ones to find,
Level 2 minima (
) are the easy ones to find,
Level 2 minima (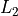 ) are much harder and Level 3 minima (
) are much harder and Level 3 minima (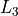 ) are much, much harder. As far as I understand,
the global optimum of all functions in this benchmark suite is a Level 3 minimum.
) are much, much harder. As far as I understand,
the global optimum of all functions in this benchmark suite is a Level 3 minimum.
This test function generator is also very particular as the problem dimensionality is a consequence of other user-defined parameters, although the relationship between the dimensionality and those other settings is fairly straightforward and can be reverse-engineered: in this way, we can provide a desired dimensionality and adapt the other parameters to fit the generator.
As said above, there is a number of user-selectable parameters:
 : the number of basic variables. Basic variables are those on which the basic multidimensional composition
functions depend.
: the number of basic variables. Basic variables are those on which the basic multidimensional composition
functions depend. 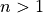 .
.
Note that they are not the unique variables of the test functions, other
variables have been introduced to combine different components of the test functions (the overall number 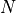 of variables
on which the test functions depend can be seen in the formula below).
of variables
on which the test functions depend can be seen in the formula below).
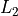 : it is the parameter which controls the number of local minimizers at Level 2.
: it is the parameter which controls the number of local minimizers at Level 2.
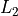 is constrained to belong to the interval
is constrained to belong to the interval ![\left[1, 2^{n+1}-1 \right]](_images/math/0ee6c13d6d9e33b34c658a258c89f20935220664.png) .
.
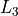 : the number of local minimizers at level 3. In view of the high difficulty introduced by local minimizers
at Level 3, the paper sets that
: the number of local minimizers at level 3. In view of the high difficulty introduced by local minimizers
at Level 3, the paper sets that 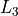 is constrained to belong to the interval
is constrained to belong to the interval ![\left[1, \sqrt{n} \right]](_images/math/cda0fc07524080cd8506bfe17dccd6fdc58fb724.png) .
.
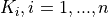 : the oscillation frequencies in the one-dimensional components of the composition functions.
The user has the option of fixing them all equal to a given value
: the oscillation frequencies in the one-dimensional components of the composition functions.
The user has the option of fixing them all equal to a given value ![K \in \left[10, 20\right]](_images/math/6a2d7302fa93ae7498e182f42b1c273615965fd2.png) or to let the value of each
of them be randomly chosen in the above interval.
or to let the value of each
of them be randomly chosen in the above interval.
The random choice of these values is a further source of difficulty because it introduces an anisotropic behavior of the function, i.e., a different behavior along distinct directions.
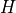 : the oscillation width: It controls the height of the barriers between neighbor local minimizers at Level 1
in the one-dimensional components of the composition functions.
: the oscillation width: It controls the height of the barriers between neighbor local minimizers at Level 1
in the one-dimensional components of the composition functions.
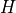 is constrained to belong to the interval
is constrained to belong to the interval ![\left[10, 30\right]](_images/math/839642947172c3b7a6a8f55e5b17c706581ebf08.png)
Once all these settings are selected, we can actually derive the dimensionality of the problem by the following formula:
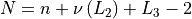
Where 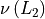 is the number of ones in the binary representation of
is the number of ones in the binary representation of 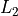 .
Armed with all this settings (and their constraints), we can actually reverse the formula above and generate quite a few
test function by providing
.
Armed with all this settings (and their constraints), we can actually reverse the formula above and generate quite a few
test function by providing 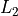 ,
, 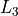 and the dimensionality
and the dimensionality 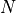 , then checking that the number
of basic variables
, then checking that the number
of basic variables  satisfies its constraints.
satisfies its constraints.
Note
The GlobOpt test suite is advertised as “Unconstrained Global Optimization Test Suite”; however, one of the
main points in the paper linked above mathematically demonstrates that, even if we do not know where the exact position of the global
minimum is, the algorithm guarantees that the global minimizer of the test functions lies in the interior of a sphere
centered at the origin and with radius 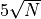 . So it was easy to assign bounds for the solvers by following
this simple procedure.
. So it was easy to assign bounds for the solvers by following
this simple procedure.
The other interesting aspect of the GlobOpt generator is that, assuming we will keep the settings for 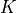 and
and
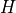 fixed and constants, then the number of “valid” test functions that can be generated is quite limited, as the constraints on the
other user-settable parameters (
fixed and constants, then the number of “valid” test functions that can be generated is quite limited, as the constraints on the
other user-settable parameters ( ,
, 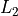 and
and 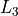 ) are stringent. This can be seen in Figure 3.2 below.
) are stringent. This can be seen in Figure 3.2 below.
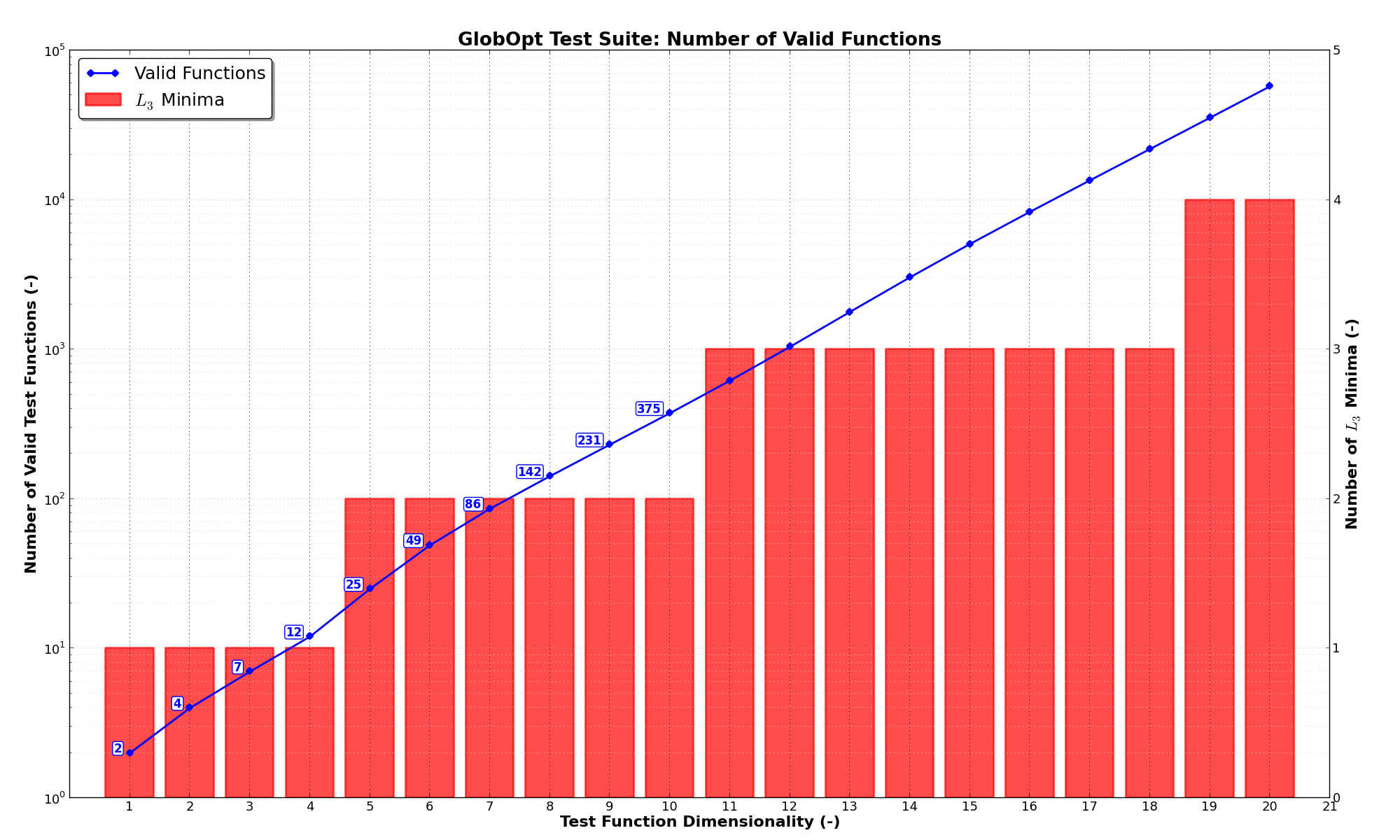
Figure 3.2: Number of “valid” test functions in the GlobOpt test suite
That said, I had no plan to keep the settings for 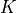 and
and 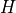 fixed and constants. My approach has been the following:
fixed and constants. My approach has been the following:
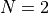 and
and 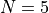
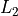 and
and 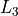 are varied independently from their maximum allowable value to the minimum (thus generating very
tough problems)
are varied independently from their maximum allowable value to the minimum (thus generating very
tough problems) is either varied randomly inside the C++ code (by setting R = 0 in the Cython wrapper) or
it can assume one value of either 10, 15 or 20.
is either varied randomly inside the C++ code (by setting R = 0 in the Cython wrapper) or
it can assume one value of either 10, 15 or 20. can assume one value of either 10, 20 or 30.
can assume one value of either 10, 20 or 30.With all these variable settings, I generated 72 valid test function per dimension, thus the current GlobOpt test suite contains 288 benchmark functions.
A few examples of 2D benchmark functions created with the GlobOpt generator can be seen in Figure 3.3.

GlobOpt Function 9 |
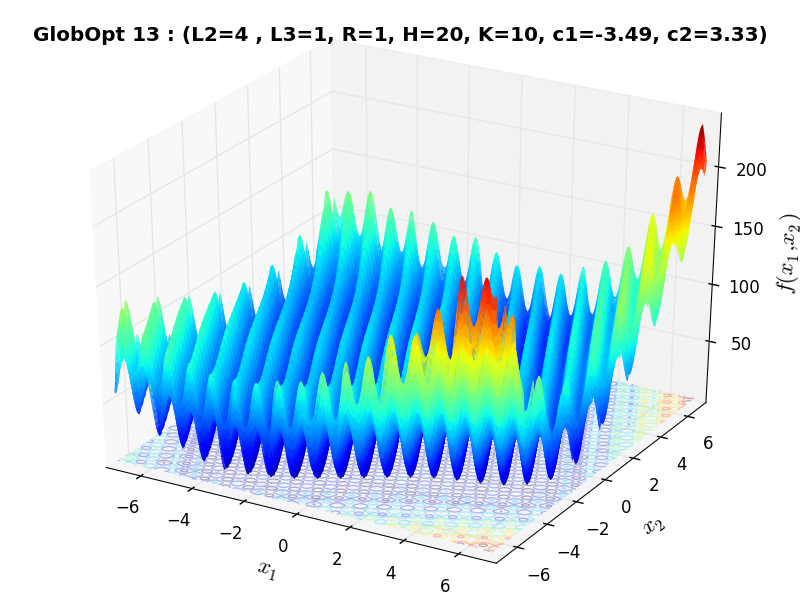
GlobOpt Function 13 |
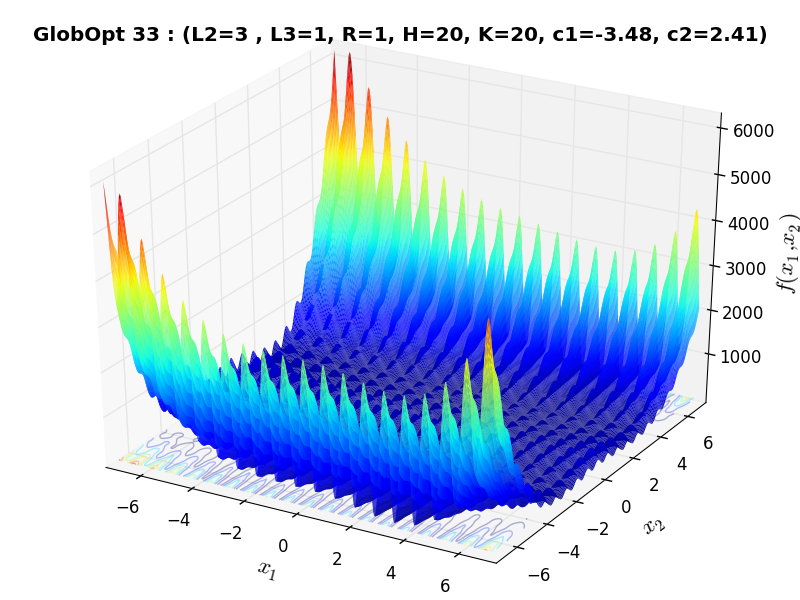
GlobOpt Function 33 |
GlobOpt Function 48 |
GlobOpt Function 60 |
GlobOpt Function 65 |
 General Solvers Performances¶
General Solvers Performances¶Table 3.1 below shows the overall success of all Global Optimization algorithms, considering every benchmark function,
for a maximum allowable budget of  .
.
Again, the GlobOpt benchmark suite is a very hard test suite, more than the GKLS one was, as the best solver (CRS2) only manages to find the global minimum in 13.9% of the cases, followed at a distance by BasinHopping and much further down by MCS and BiteOpt.
Note
The reported number of functions evaluations refers to successful optimizations only.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 1.39% | 1,232 |
| BasinHopping | 10.42% | 1,097 |
| BiteOpt | 6.25% | 1,020 |
| CMA-ES | 0.35% | 1,167 |
| CRS2 | 13.89% | 1,201 |
| DE | 4.51% | 1,677 |
| DIRECT | 3.82% | 1,306 |
| DualAnnealing | 5.56% | 864 |
| LeapFrog | 1.39% | 268 |
| MCS | 6.94% | 1,170 |
| PSWARM | 0.00% | 0 |
| SCE | 0.35% | 1,598 |
| SHGO | 0.69% | 47 |
These results are also depicted in Figure 3.4, which shows that CRS2 is the better-performing optimization algorithm, followed by BasinHopping and MCS.
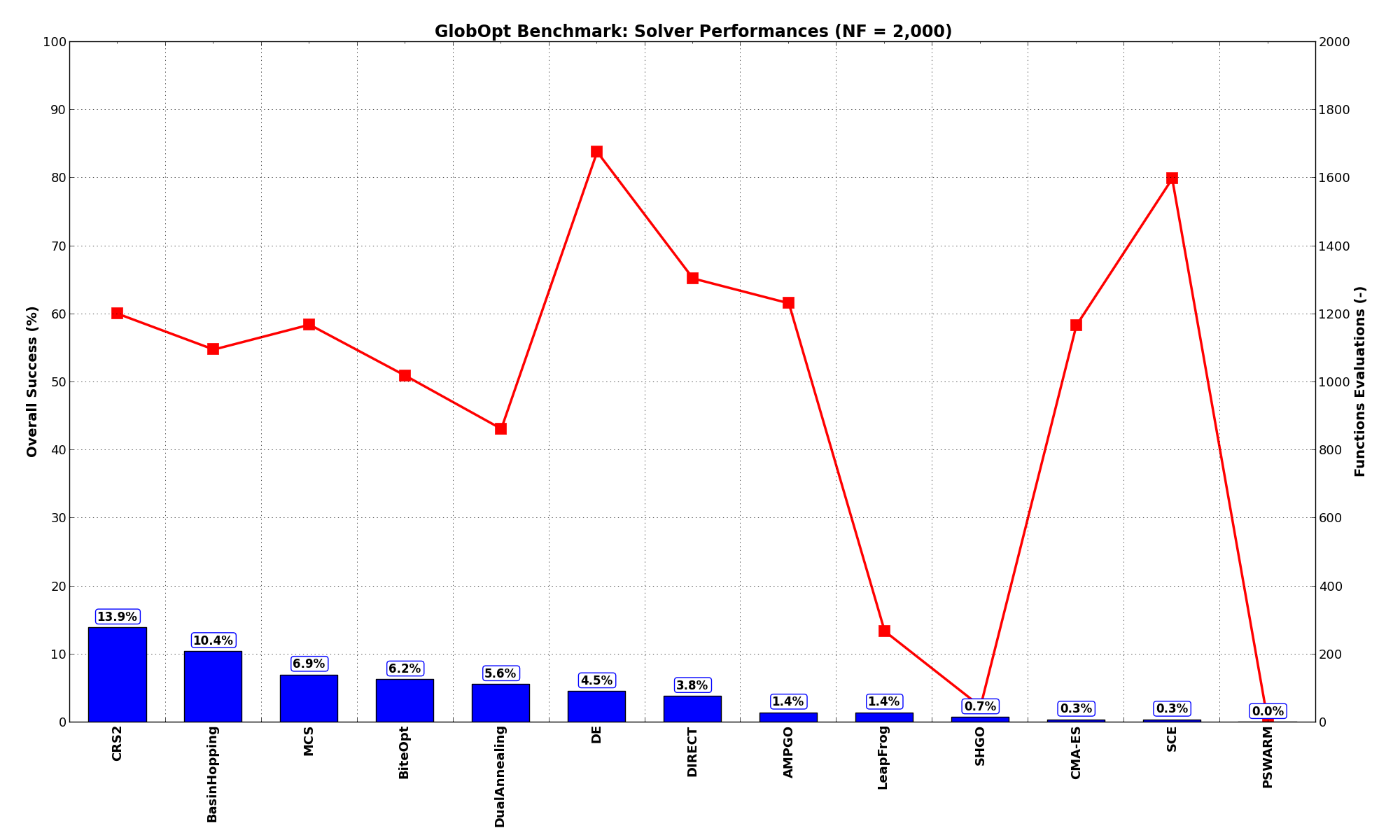
Figure 3.4: Optimization algorithms performances on the GlobOpt test suite at 
Pushing the available budget to a very generous  , the results show MCS taking the lead
on other solvers (about 3% more problems solved compared to the second best, BasinHopping). The results are also
shown visually in Figure 3.5.
, the results show MCS taking the lead
on other solvers (about 3% more problems solved compared to the second best, BasinHopping). The results are also
shown visually in Figure 3.5.
| Optimization Method | Overall Success (%) | Functions Evaluations |
|---|---|---|
| AMPGO | 5.90% | 3,955 |
| BasinHopping | 20.83% | 2,250 |
| BiteOpt | 10.76% | 2,624 |
| CMA-ES | 3.12% | 6,164 |
| CRS2 | 18.40% | 2,366 |
| DE | 10.76% | 4,427 |
| DIRECT | 10.42% | 3,529 |
| DualAnnealing | 7.29% | 1,340 |
| LeapFrog | 1.39% | 268 |
| MCS | 23.96% | 3,754 |
| PSWARM | 7.29% | 3,585 |
| SCE | 3.82% | 5,893 |
| SHGO | 3.82% | 5,289 |
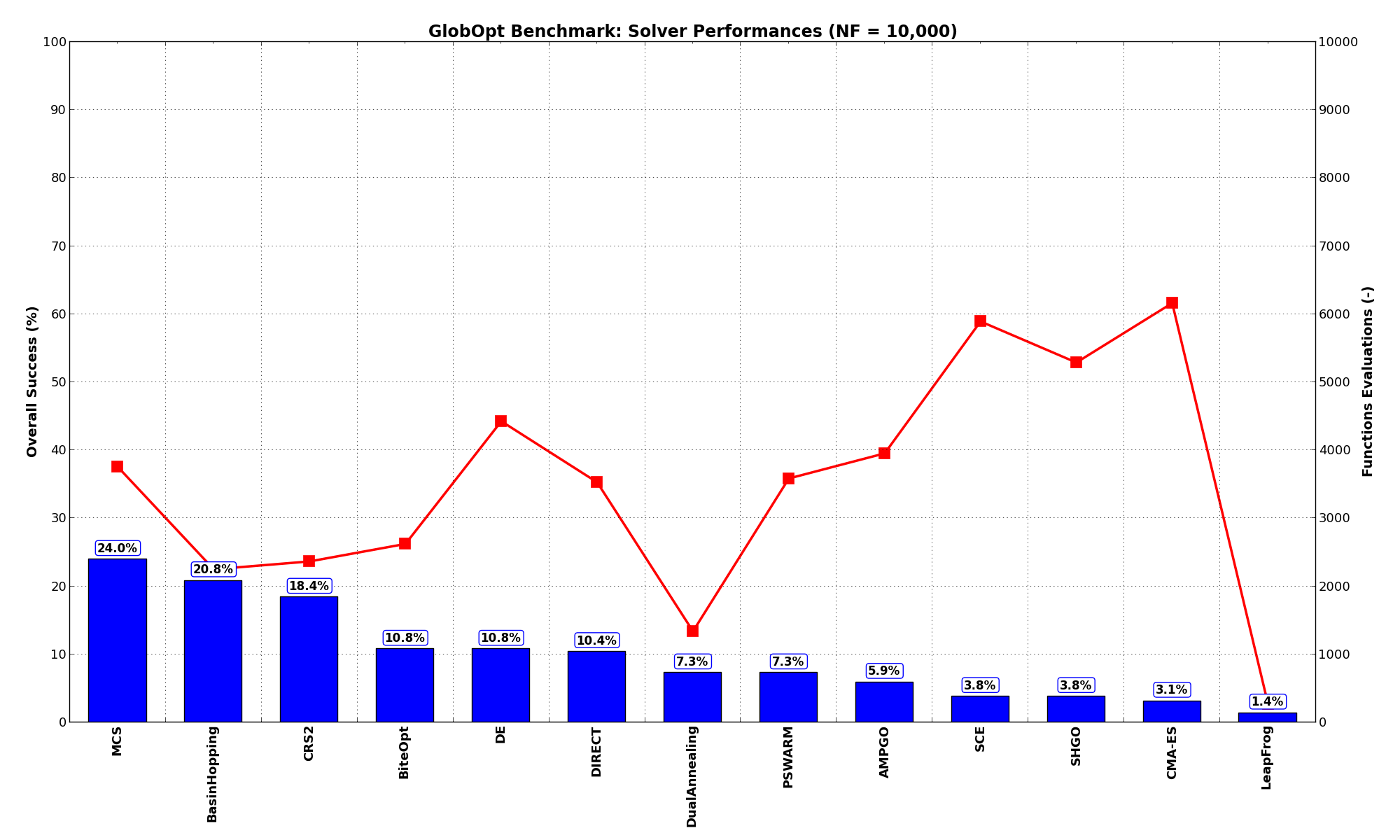
Figure 3.5: Optimization algorithms performances on the GlobOpt test suite at 
Since I was super annoyed that none of the Global Optimization algorithms were doing any better than 24% solved problems
even with a very generous budget of function evaluations of  , for this test suite only I decided
to push the limits even more and allow an extended
, for this test suite only I decided
to push the limits even more and allow an extended 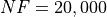 and
and 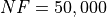 budget limit, just to
see if any difference could be spotted - or any change in the algorithm performances.
budget limit, just to
see if any difference could be spotted - or any change in the algorithm performances.
Alas, as Figure 3.6 shows, even the best solver ( MCS) cannot get better than 36.5% of the problems solved. What is interesting, though, is the much improved performances of one of the SciPy solvers, SHGO, which moves from 4% to 29% of all global minimum found.
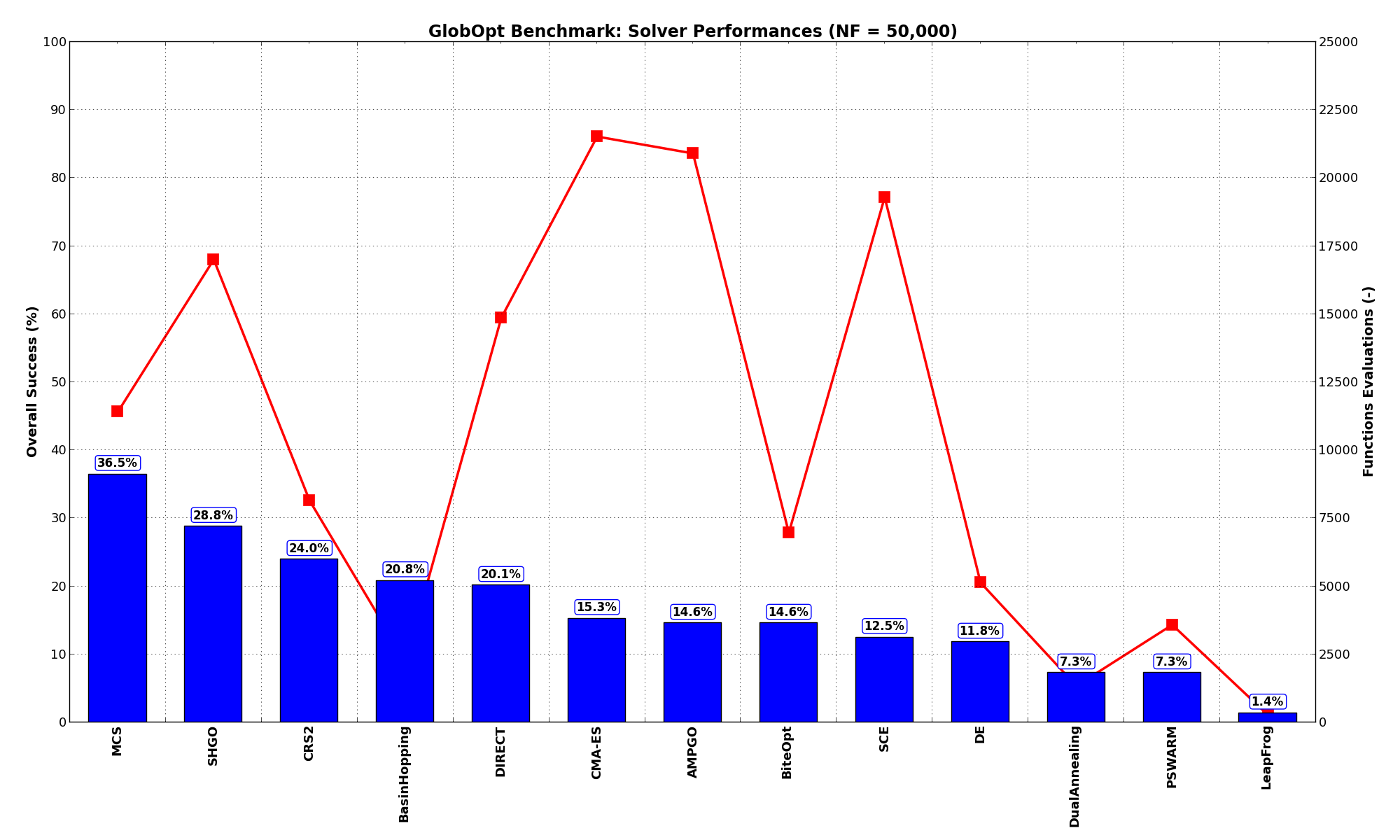
Figure 3.6: Optimization algorithms performances on the GlobOpt test suite at 
 Sensitivities on Functions Evaluations Budget¶
Sensitivities on Functions Evaluations Budget¶It is also interesting to analyze the success of an optimization algorithm based on the fraction (or percentage) of problems solved given a fixed number of allowed function evaluations, let’s say 100, 200, 300,... 2000, 5000, 10000.
In order to do that, we can present the results using two different types of visualizations. The first one is some sort of “small multiples” in which each solver gets an individual subplot showing the improvement in the number of solved problems as a function of the available number of function evaluations - on top of a background set of grey, semi-transparent lines showing all the other solvers performances.
This visual gives an indication of how good/bad is a solver compared to all the others as function of the budget available. Results are shown in Figure 3.7.
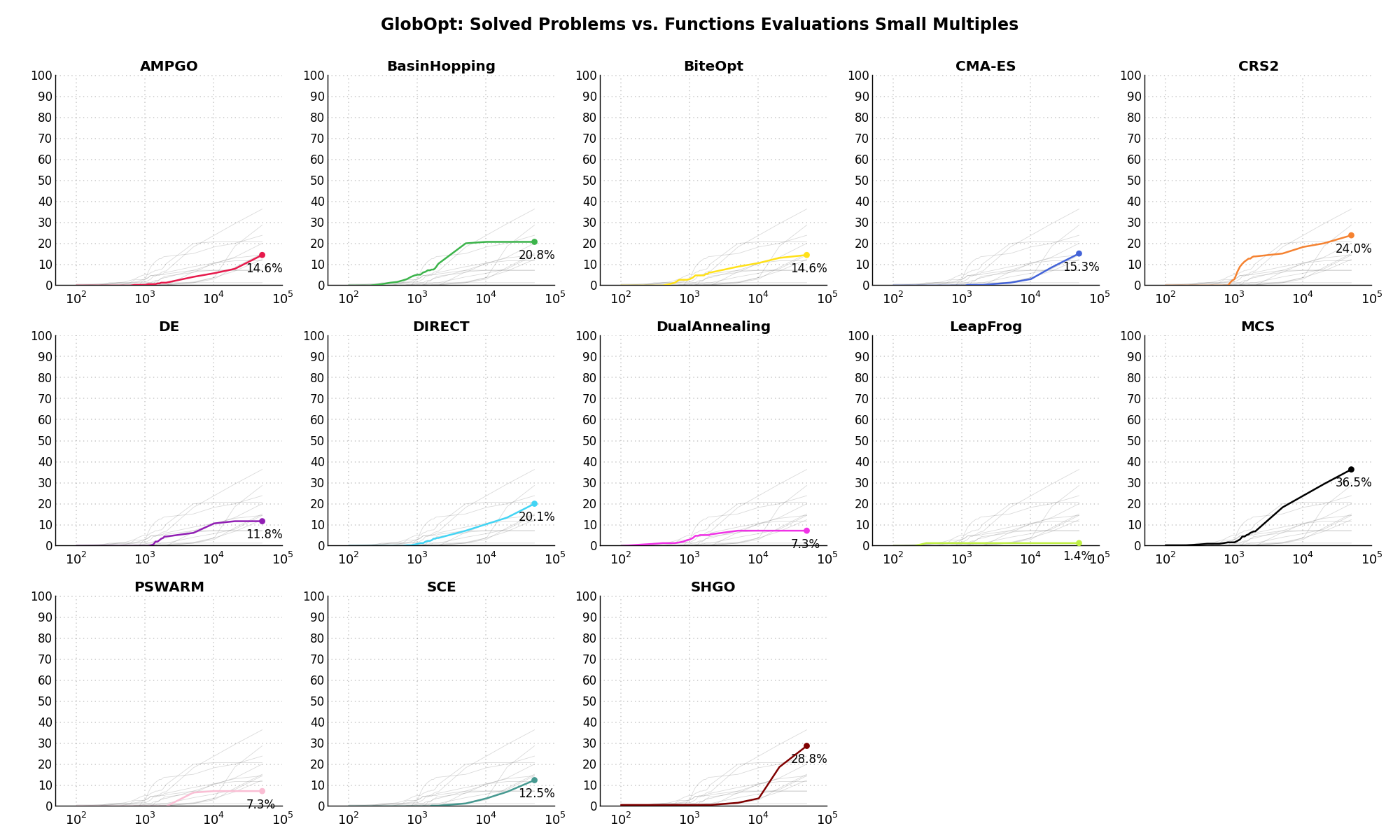
Figure 3.7: Percentage of problems solved given a fixed number of function evaluations on the GlobOpt test suite
The second type of visualization is sometimes referred as “Slopegraph” and there are many variants on the plot layout and appearance that we can implement. The version shown in Figure 3.8 aggregates all the solvers together, so it is easier to spot when a solver overtakes another or the overall performance of an algorithm while the available budget of function evaluations changes.
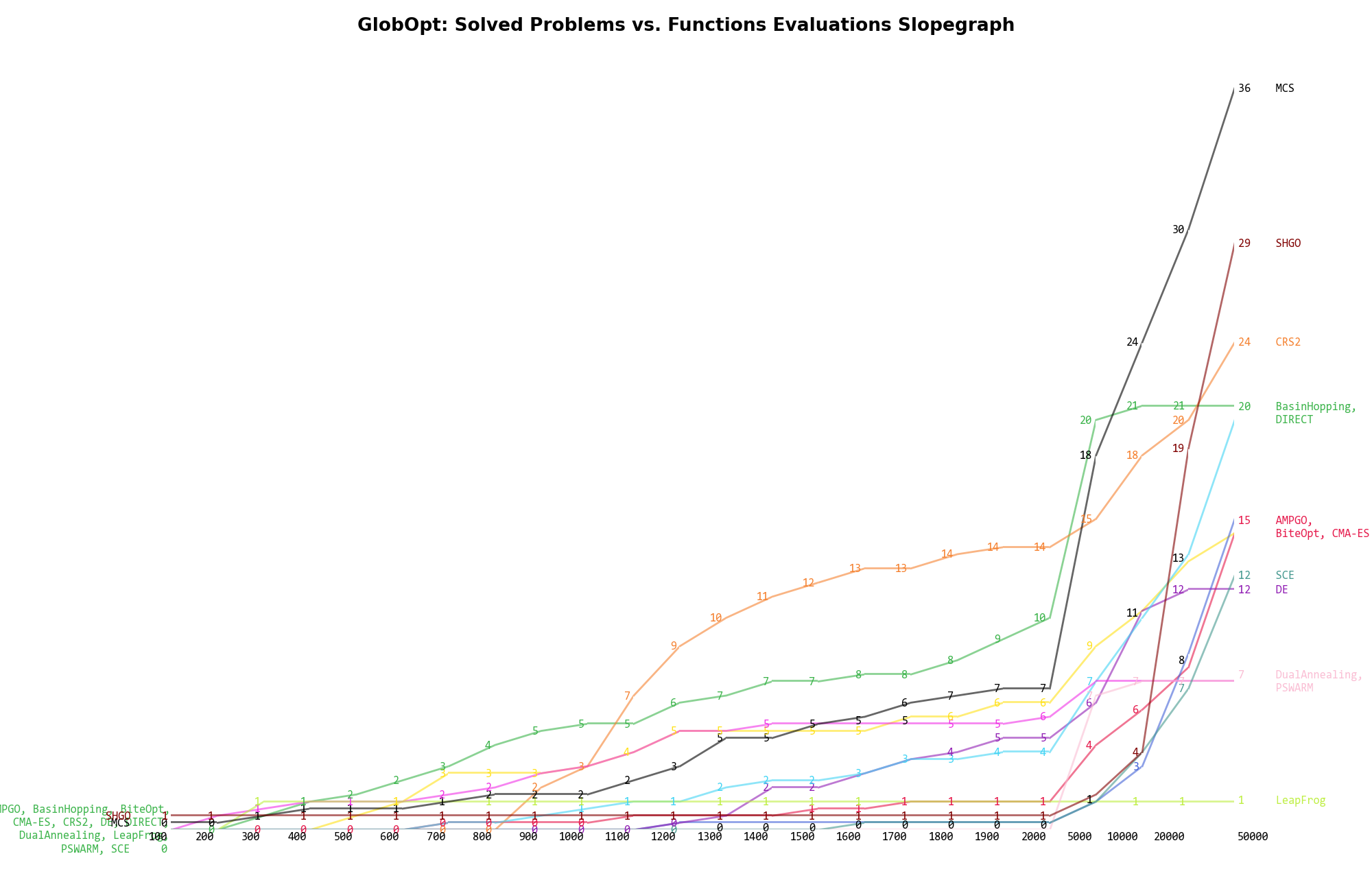
Figure 3.8: Percentage of problems solved given a fixed number of function evaluations on the GlobOpt test suite
A few obvious conclusions we can draw from these pictures are:
 are CRS2 and BasinHopping, with meagre 14% and 10% solved problems respectively.
are CRS2 and BasinHopping, with meagre 14% and 10% solved problems respectively. Dimensionality Effects¶
Dimensionality Effects¶Since I used the GlobOpt test suite to generate test functions with dimensionality ranging from 2 to 5, it is interesting to take a look at the solvers performances as a function of the problem dimensionality. Of course, in general it is to be expected that for larger dimensions less problems are going to be solved - although it is not always necessarily so as it also depends on the function being generated. Results are shown in Table 3.3 .
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 1.4 | 4.2 | 0.0 | 0.0 | 1.4 |
| BasinHopping | 40.3 | 1.4 | 0.0 | 0.0 | 10.4 |
| BiteOpt | 25.0 | 0.0 | 0.0 | 0.0 | 6.2 |
| CMA-ES | 1.4 | 0.0 | 0.0 | 0.0 | 0.3 |
| CRS2 | 52.8 | 2.8 | 0.0 | 0.0 | 13.9 |
| DE | 18.1 | 0.0 | 0.0 | 0.0 | 4.5 |
| DIRECT | 15.3 | 0.0 | 0.0 | 0.0 | 3.8 |
| DualAnnealing | 22.2 | 0.0 | 0.0 | 0.0 | 5.6 |
| LeapFrog | 5.6 | 0.0 | 0.0 | 0.0 | 1.4 |
| MCS | 26.4 | 1.4 | 0.0 | 0.0 | 6.9 |
| PSWARM | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| SCE | 1.4 | 0.0 | 0.0 | 0.0 | 0.3 |
| SHGO | 2.8 | 0.0 | 0.0 | 0.0 | 0.7 |
Figure 3.9 shows the same results in a visual way.
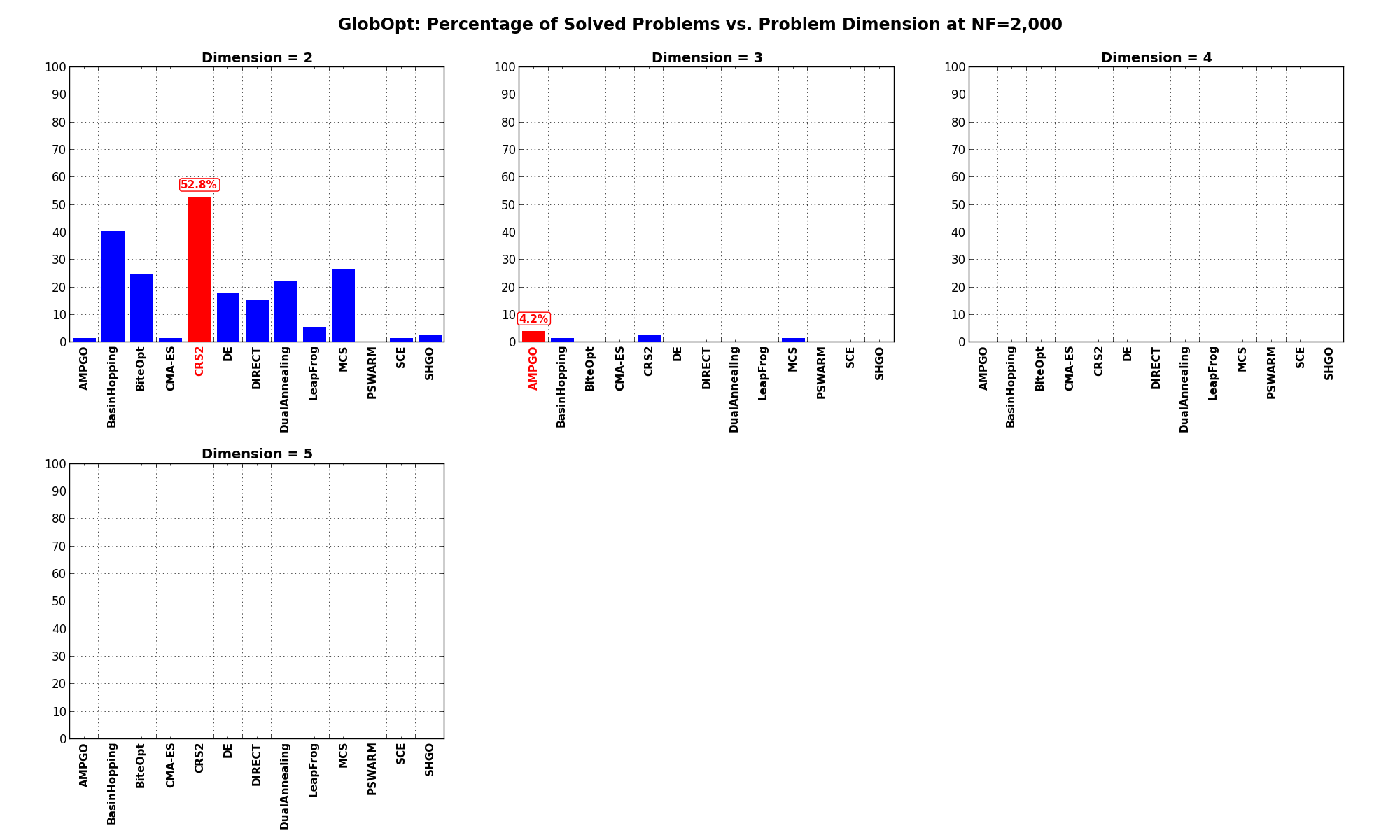
Figure 3.9: Percentage of problems solved as a function of problem dimension for the GlobOpt test suite at 
What we can infer from the table and the figure is that, for lower dimensionality problems (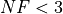 ), the CRS2
algorithm has a significant advantage over all other algorithms, although the SciPy optimizer BasinHopping is not
too far behind. For higher dimensionality problems (
), the CRS2
algorithm has a significant advantage over all other algorithms, although the SciPy optimizer BasinHopping is not
too far behind. For higher dimensionality problems (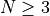 ), the performance degradations are noticeable for all solvers, and none
of the solvers is able to show any meaningful and strong result.
), the performance degradations are noticeable for all solvers, and none
of the solvers is able to show any meaningful and strong result.
Pushing the available budget to a very generous  , the results show MCS taking a significant lead
on other solvers, but only on very low dimensionality problems with
, the results show MCS taking a significant lead
on other solvers, but only on very low dimensionality problems with 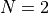 . For higher dimensionality problems
a solver like CRS2 or DE is a much safe option, although the performances are not spectacular at all.
. For higher dimensionality problems
a solver like CRS2 or DE is a much safe option, although the performances are not spectacular at all.
The results for the benchmarks at  are displayed in Table 3.4 and Figure 3.10.
are displayed in Table 3.4 and Figure 3.10.
| Solver | N = 2 | N = 3 | N = 4 | N = 5 | Overall |
|---|---|---|---|---|---|
| AMPGO | 18.1 | 5.6 | 0.0 | 0.0 | 5.9 |
| BasinHopping | 65.3 | 11.1 | 5.6 | 1.4 | 20.8 |
| BiteOpt | 37.5 | 4.2 | 0.0 | 1.4 | 10.8 |
| CMA-ES | 12.5 | 0.0 | 0.0 | 0.0 | 3.1 |
| CRS2 | 52.8 | 12.5 | 8.3 | 0.0 | 18.4 |
| DE | 20.8 | 12.5 | 8.3 | 1.4 | 10.8 |
| DIRECT | 34.7 | 6.9 | 0.0 | 0.0 | 10.4 |
| DualAnnealing | 29.2 | 0.0 | 0.0 | 0.0 | 7.3 |
| LeapFrog | 5.6 | 0.0 | 0.0 | 0.0 | 1.4 |
| MCS | 84.7 | 11.1 | 0.0 | 0.0 | 24.0 |
| PSWARM | 26.4 | 2.8 | 0.0 | 0.0 | 7.3 |
| SCE | 15.3 | 0.0 | 0.0 | 0.0 | 3.8 |
| SHGO | 15.3 | 0.0 | 0.0 | 0.0 | 3.8 |
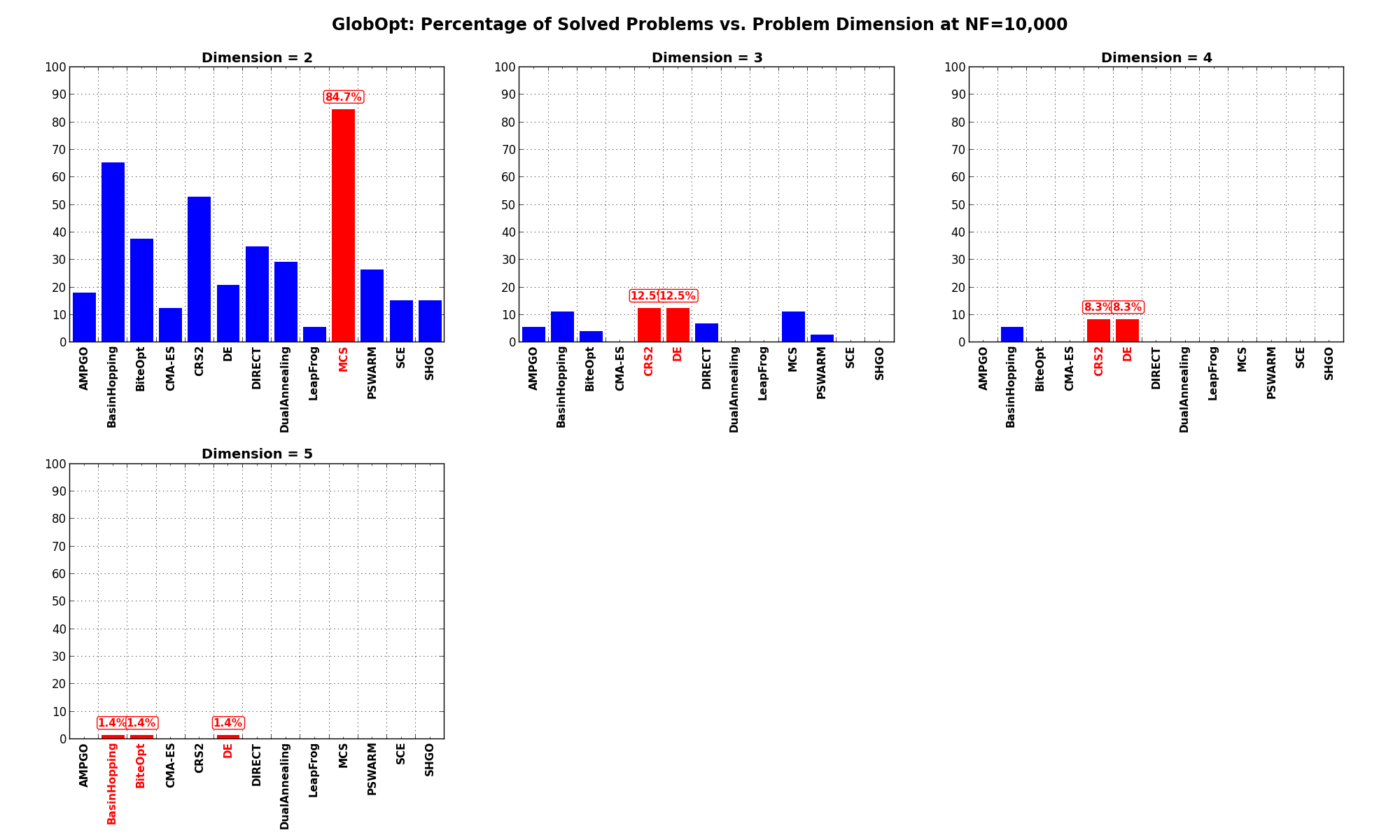
Figure 3.10: Percentage of problems solved as a function of problem dimension for the GlobOpt test suite at 