 N-D Test Functions Z¶
N-D Test Functions Z¶Zacharov test objective function.
This class defines the Zacharov global optimization problem. This is a multimodal minimization problem defined as follows:
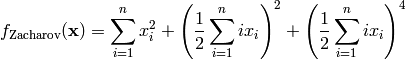
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 10]](_images/math/98df04fbd9b8266181439af788bf1880288e02c8.png) for
for  .
.
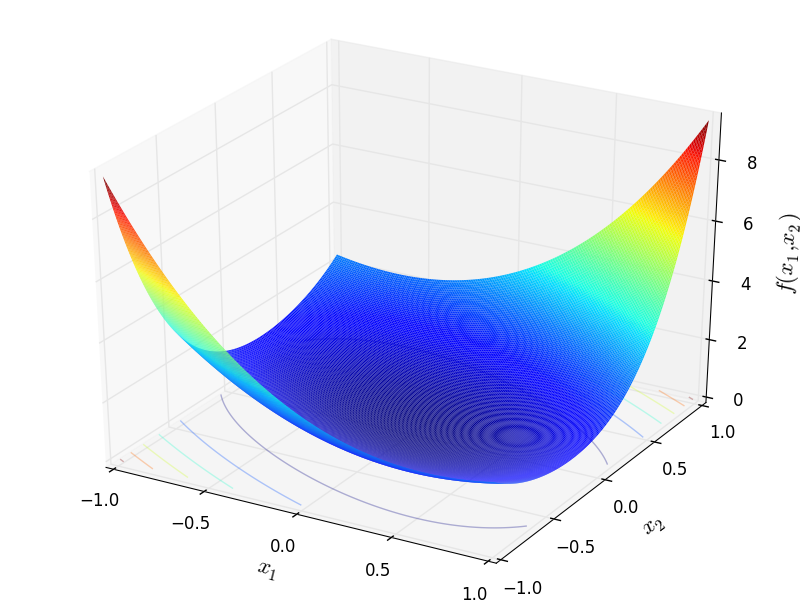
Two-dimensional Zacharov function
Global optimum:  for
for 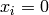 for
for 
ZeroSum test objective function.
This class defines the ZeroSum global optimization problem. This is a multimodal minimization problem defined as follows:
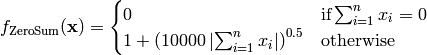
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
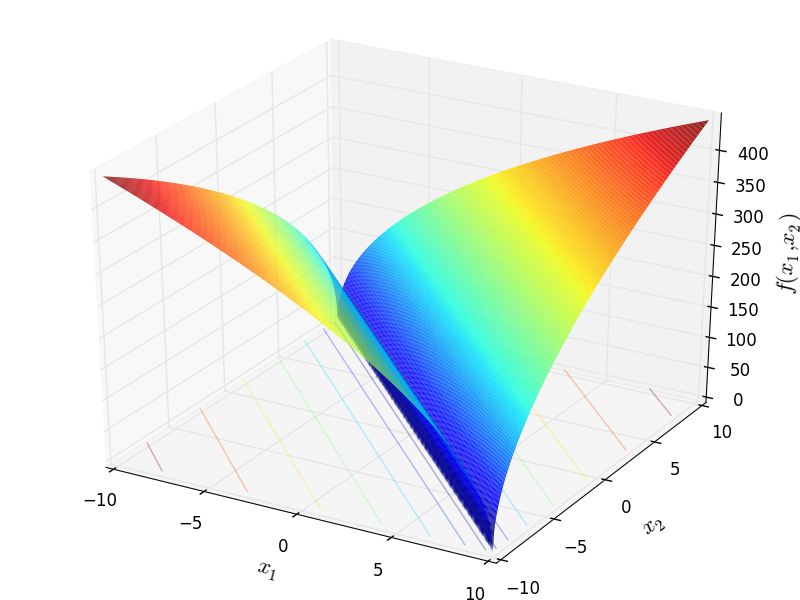
Two-dimensional ZeroSum function
Global optimum:  where
where 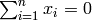
Zettl test objective function.
This class defines the Zettl global optimization problem. This is a multimodal minimization problem defined as follows:
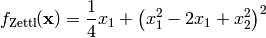
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 5]](_images/math/401922216113b08838e8dba8860ce460deaee9fc.png) for
for  .
.
Two-dimensional Zettl function
Global optimum:  for
for ![\mathbf{x} = [-0.029896, 0.0]](_images/math/3c0bcce1d68730a4a40a1c5a7c59f06cf56a2913.png)
Zimmerman test objective function.
This class defines the Zimmerman global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Zimmerman}}(\mathbf{x}) = \max \left[Zh1(x), Zp(Zh2(x))\textrm{sgn}(Zh2(x)), Zp(Zh3(x)) \textrm{sgn}(Zh3(x)), Zp(-x_1)\textrm{sgn}(x_1), Zp(-x_2)\textrm{sgn}(x_2) \right]](_images/math/569998ea23b73cf75dfe10130524b32c04a1e7fc.png)
Where, in this exercise:
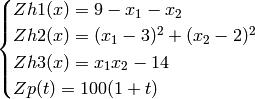
Where 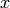 is a vector and
is a vector and 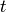 is a scalar.
is a scalar.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 100]](_images/math/dff6d980169d585461c8b4dce088b6e71c019f70.png) for
for  .
.
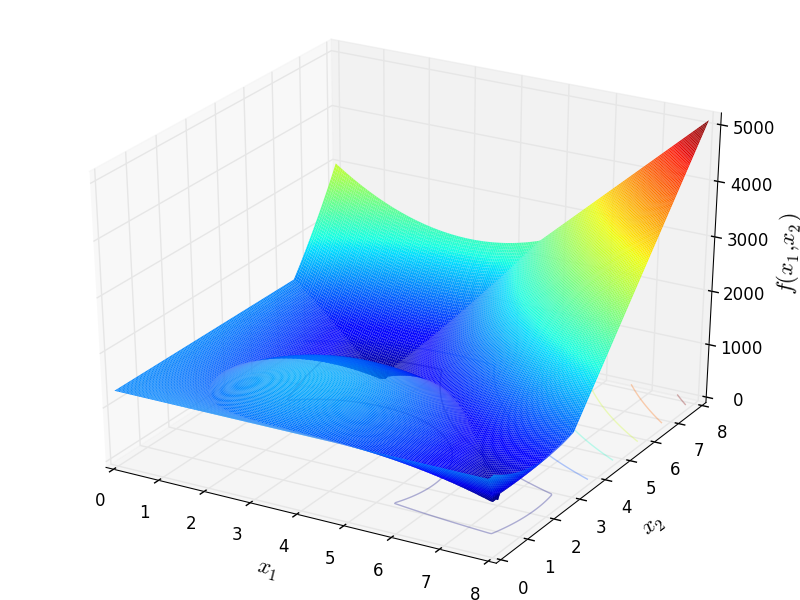
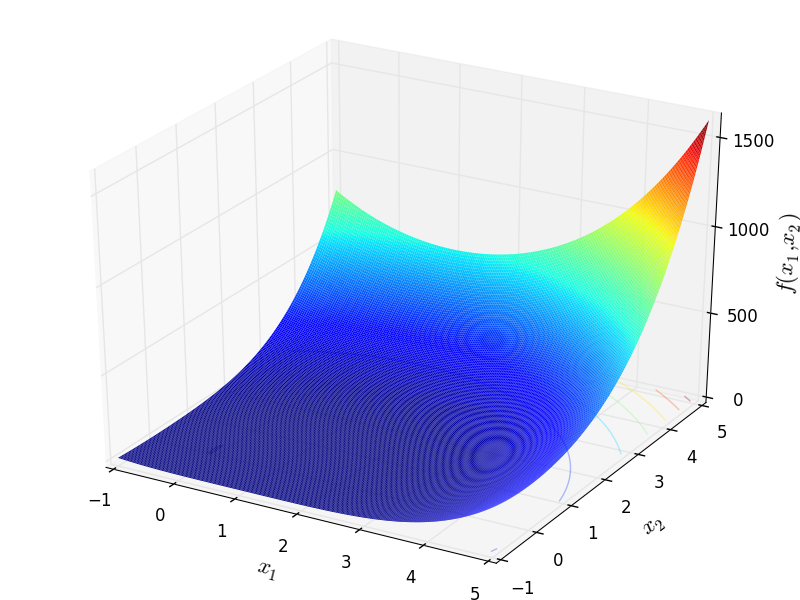
Two-dimensional Zimmerman function
Global optimum:  for
for ![\mathbf{x} = [7, 2]](_images/math/0acd03126b89cf64488b9d0539cfb3e97c1b15bf.png)
Zettl test objective function.
This class defines the Zirilli global optimization problem. This is a unimodal minimization problem defined as follows:
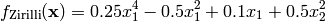
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
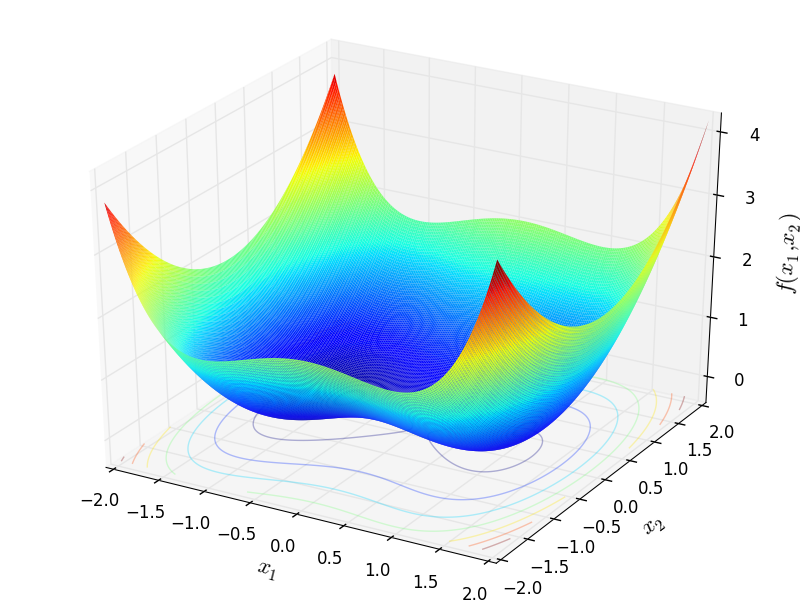
Two-dimensional Zirilli function
Global optimum: 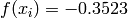 for
for ![\mathbf{x} = [-1.0465, 0]](_images/math/ef2f52e6c1900821ceb676b1a029ce8e683bcc15.png)