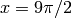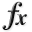1-D Test Functions¶

class go_benchmark.Problem02(dimensions=1)¶

Univariate Problem02 test objective function.

This class defines the Univariate Problem02 global optimization problem. This is a multimodal minimization problem defined as follows:

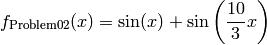
$f_{\text{Problem02}}(x) = \sin(x) + \sin \left(\frac{10}{3}x \right)$

Bound constraints: $x \in [2.7, 7.5]$

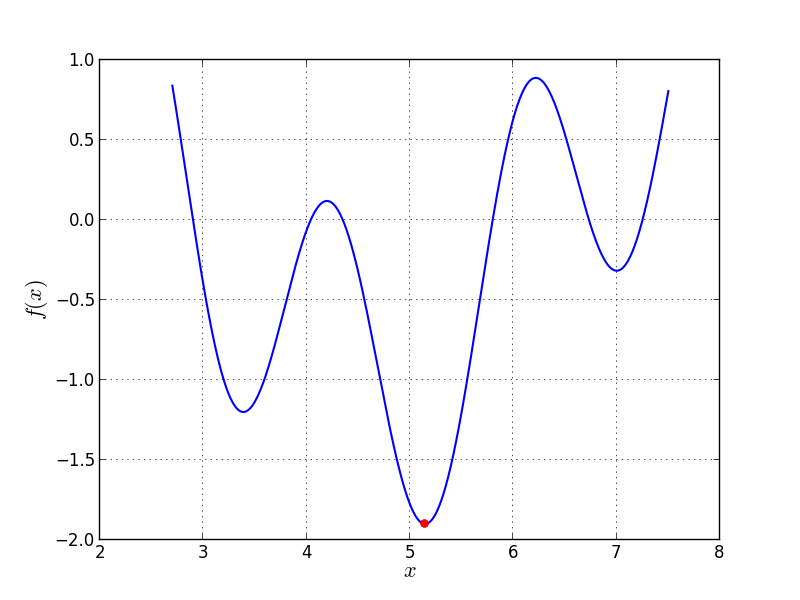
Univariate Problem02 function

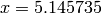
Global optimum: $f(x)=-1.899599$ for $x = 5.145735$

class go_benchmark.Problem03(dimensions=1)¶

Univariate Problem03 test objective function.

This class defines the Univariate Problem03 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem03}}(x) = - \sum_{k=1}^6 k \sin[(k+1)x+k]$

Bound constraints: $x \in [-10, 10]$

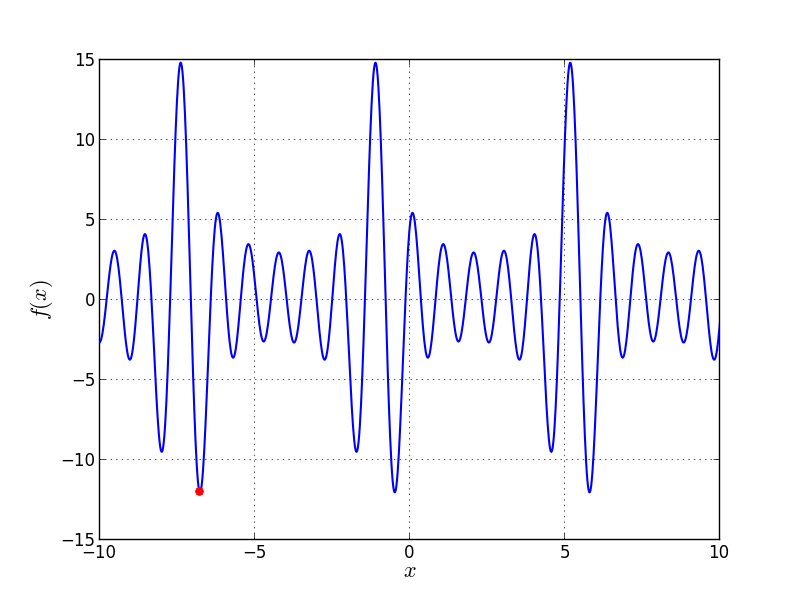
Univariate Problem03 function

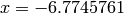
Global optimum: $f(x)=-12.03124$ for $x = -6.7745761$

class go_benchmark.Problem04(dimensions=1)¶

Univariate Problem04 test objective function.

This class defines the Univariate Problem04 global optimization problem. This is a multimodal minimization problem defined as follows:

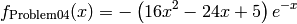
$f_{\text{Problem04}}(x) = - \left(16x^2 - 24x + 5 \right) e^{-x}$

Bound constraints: $x \in [1.9, 3.9]$

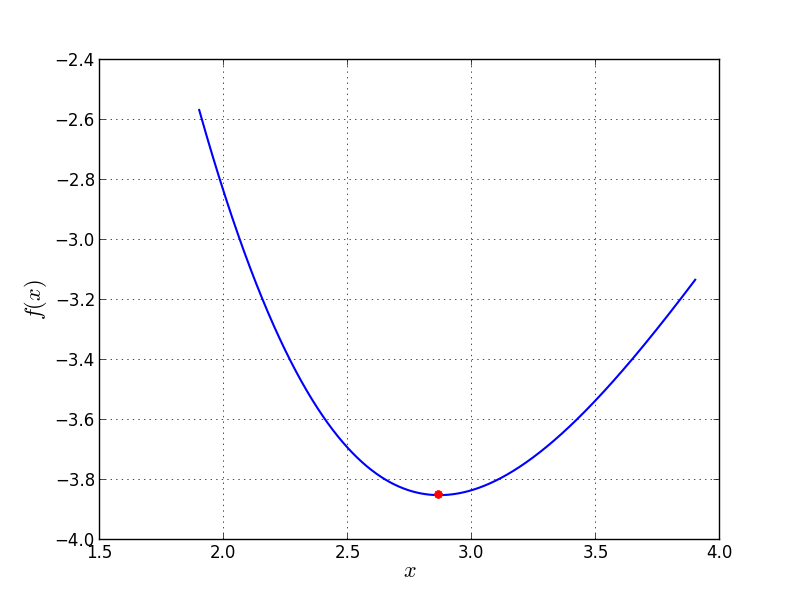
Univariate Problem04 function

Global optimum: 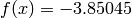$f(x)=-3.85045$ for $x = 2.868034$

class go_benchmark.Problem05(dimensions=1)¶

Univariate Problem05 test objective function.

This class defines the Univariate Problem05 global optimization problem. This is a multimodal minimization problem defined as follows:

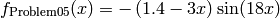
$f_{\text{Problem05}}(x) = - \left(1.4 - 3x \right) \sin(18x)$

Bound constraints: $x \in [0, 1.2]$

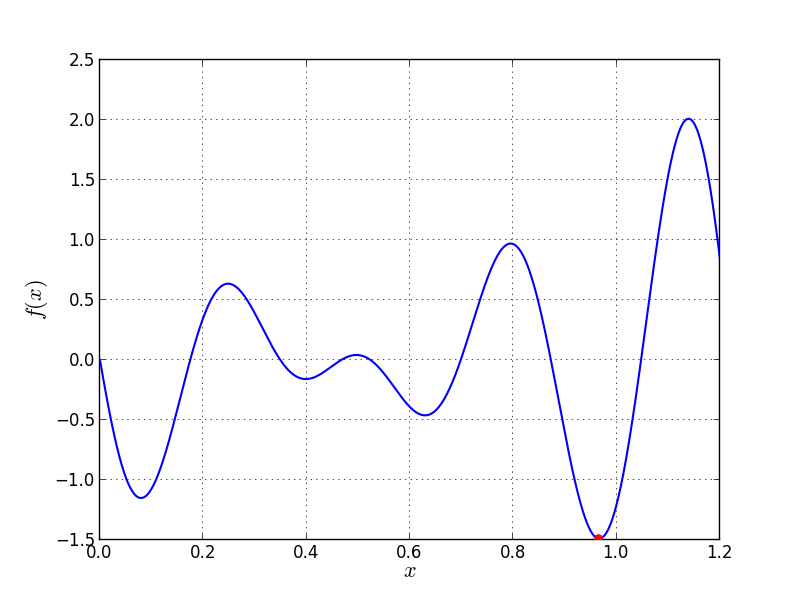
Univariate Problem05 function

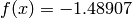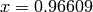
Global optimum: $f(x)=-1.48907$ for $x = 0.96609$

class go_benchmark.Problem06(dimensions=1)¶

Univariate Problem06 test objective function.

This class defines the Univariate Problem06 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem06}}(x) = - \left[x + \sin(x) \right] e^{-x^2}$

Bound constraints: $x \in [-10, 10]$

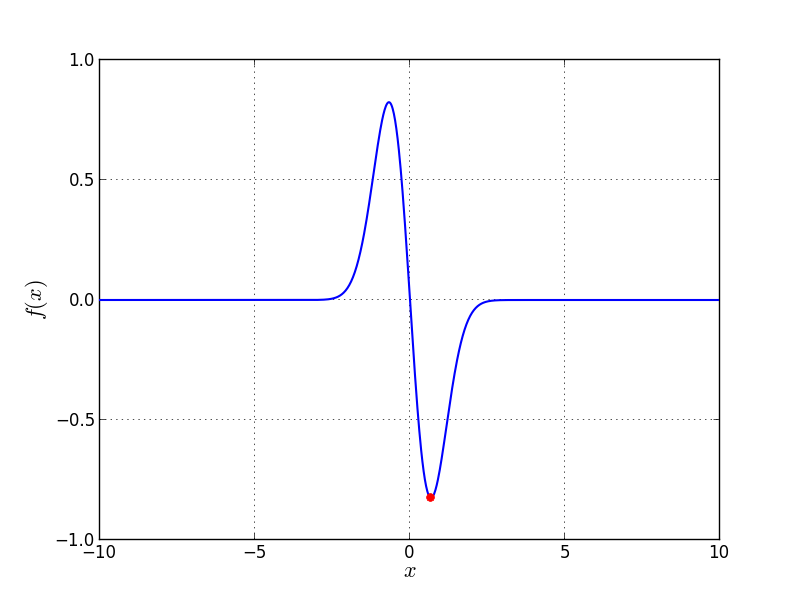
Univariate Problem06 function

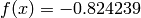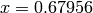
Global optimum: $f(x)=-0.824239$ for $x = 0.67956$

class go_benchmark.Problem07(dimensions=1)¶

Univariate Problem07 test objective function.

This class defines the Univariate Problem07 global optimization problem. This is a multimodal minimization problem defined as follows:

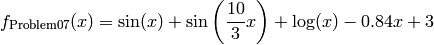
$f_{\text{Problem07}}(x) = \sin(x) + \sin \left(\frac{10}{3}x \right) + \log(x) - 0.84x + 3$

Bound constraints: $x \in [2.7, 7.5]$

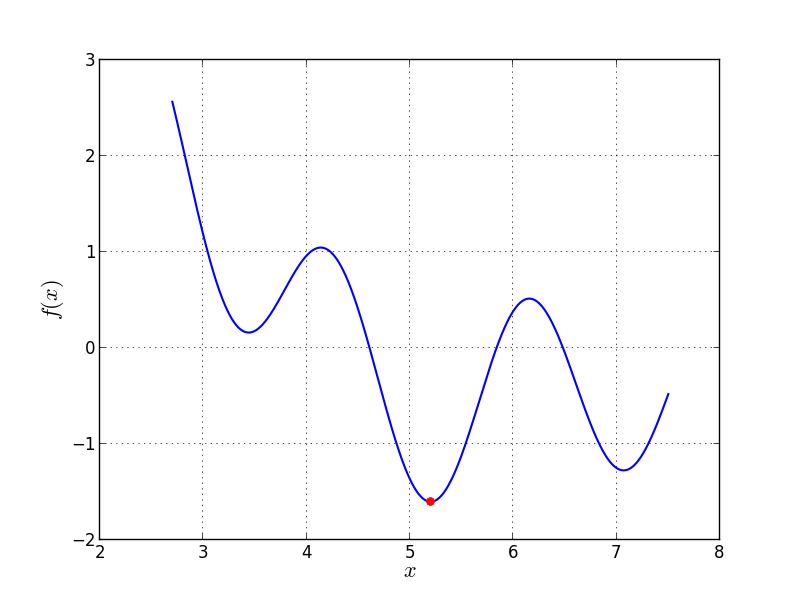
Univariate Problem07 function

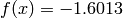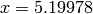
Global optimum: $f(x)=-1.6013$ for $x = 5.19978$

class go_benchmark.Problem08(dimensions=1)¶

Univariate Problem08 test objective function.

This class defines the Univariate Problem08 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem08}}(x) = - \sum_{k=1}^6 k \cos[(k+1)x+k]$

Bound constraints: $x \in [-10, 10]$

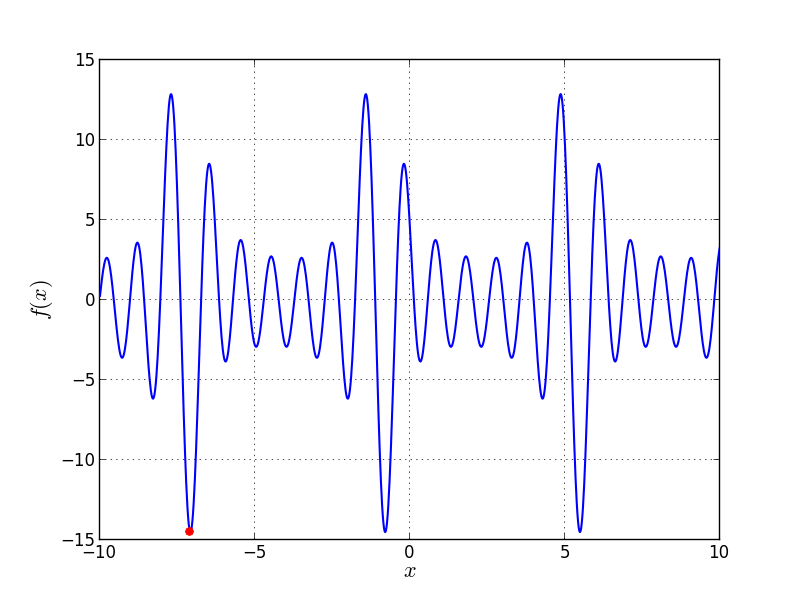
Univariate Problem08 function

Global optimum: 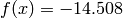$f(x)=-14.508$ for $x = -7.083506$

class go_benchmark.Problem09(dimensions=1)¶

Univariate Problem09 test objective function.

This class defines the Univariate Problem09 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem09}}(x) = \sin(x) + \sin \left(\frac{2}{3} x \right)$

Bound constraints: $x \in [3.1, 20.4]$

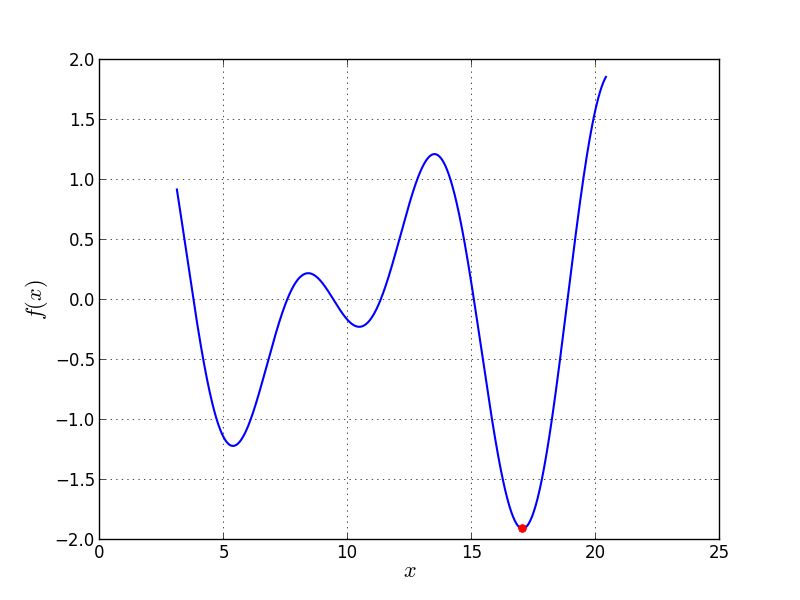
Univariate Problem09 function

Global optimum: $f(x)=-1.90596$ for $x = 17.039$

class go_benchmark.Problem10(dimensions=1)¶

Univariate Problem10 test objective function.

This class defines the Univariate Problem10 global optimization problem. This is a multimodal minimization problem defined as follows:

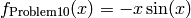
$f_{\text{Problem10}}(x) = -x\sin(x)$

Bound constraints: $x \in [0, 10]$

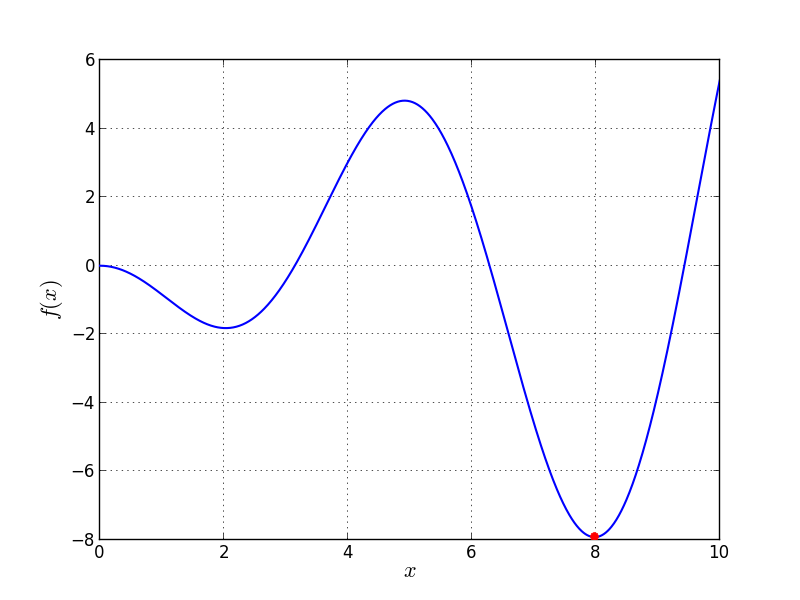
Univariate Problem10 function

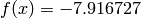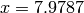
Global optimum: $f(x)=-7.916727$ for $x = 7.9787$

class go_benchmark.Problem11(dimensions=1)¶

Univariate Problem11 test objective function.

This class defines the Univariate Problem11 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem11}}(x) = 2\cos(x) + \cos(2x)$

Bound constraints: $x \in [-\pi/2, 2\pi]$

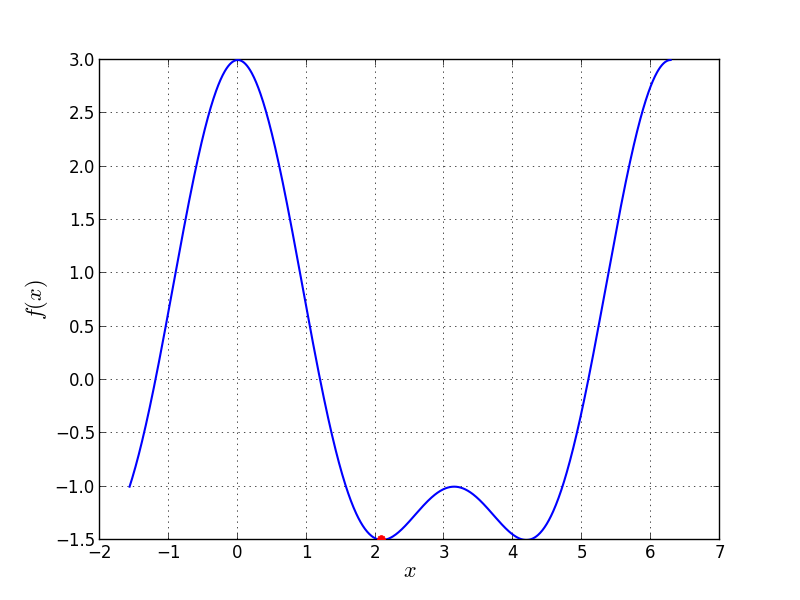
Univariate Problem11 function

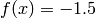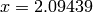
Global optimum: $f(x)=-1.5$ for $x = 2.09439$

class go_benchmark.Problem12(dimensions=1)¶

Univariate Problem12 test objective function.

This class defines the Univariate Problem12 global optimization problem. This is a multimodal minimization problem defined as follows:

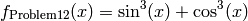
$f_{\text{Problem12}}(x) = \sin^3(x) + \cos^3(x)$

Bound constraints: $x \in [0, 2\pi]$

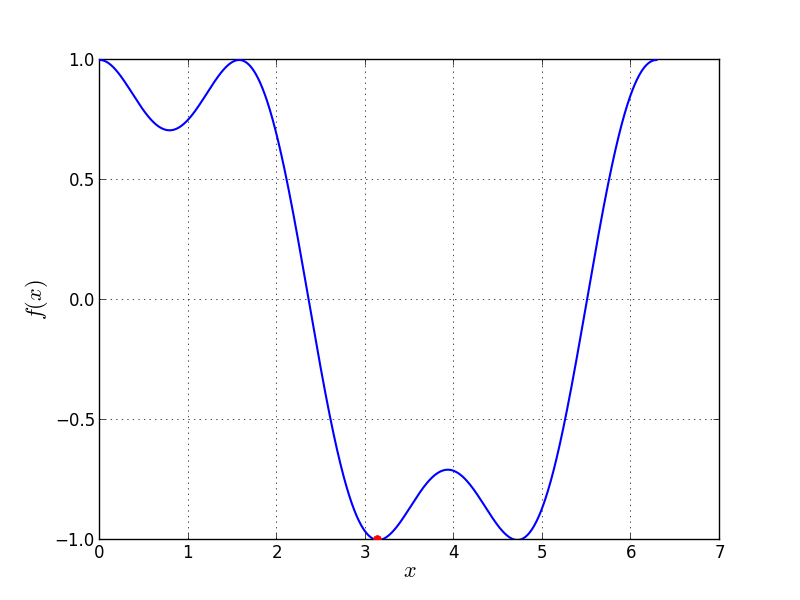
Univariate Problem12 function

Global optimum: 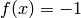$f(x)=-1$ for $x = \pi$

class go_benchmark.Problem13(dimensions=1)¶

Univariate Problem13 test objective function.

This class defines the Univariate Problem13 global optimization problem. This is a multimodal minimization problem defined as follows:

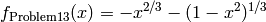
$f_{\text{Problem13}}(x) = -x^{2/3} - (1 - x^2)^{1/3}$

Bound constraints: $x \in [0.001, 0.99]$

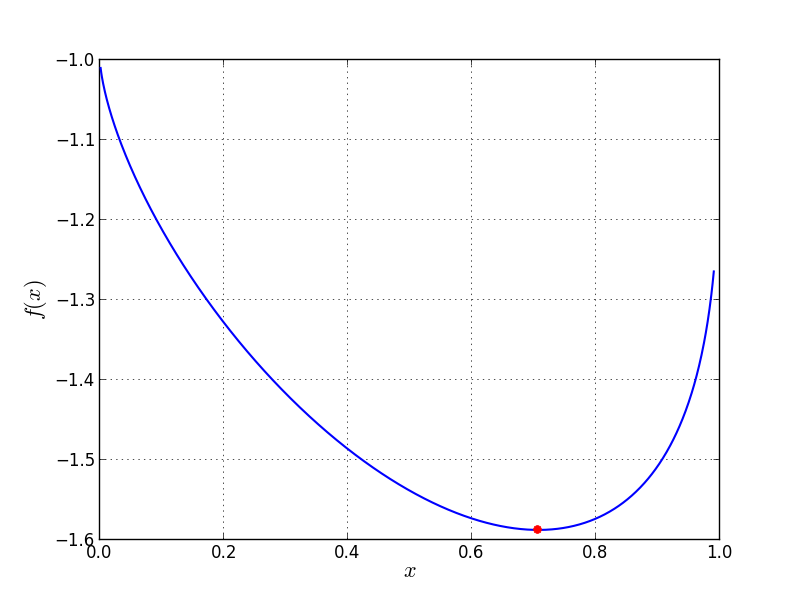
Univariate Problem13 function

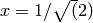
Global optimum: $f(x)=-1.5874$ for $x = 1/\sqrt(2)$

class go_benchmark.Problem14(dimensions=1)¶

Univariate Problem14 test objective function.

This class defines the Univariate Problem14 global optimization problem. This is a multimodal minimization problem defined as follows:

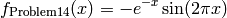
$f_{\text{Problem14}}(x) = -e^{-x} \sin(2\pi x)$

Bound constraints: $x \in [0, 4]$

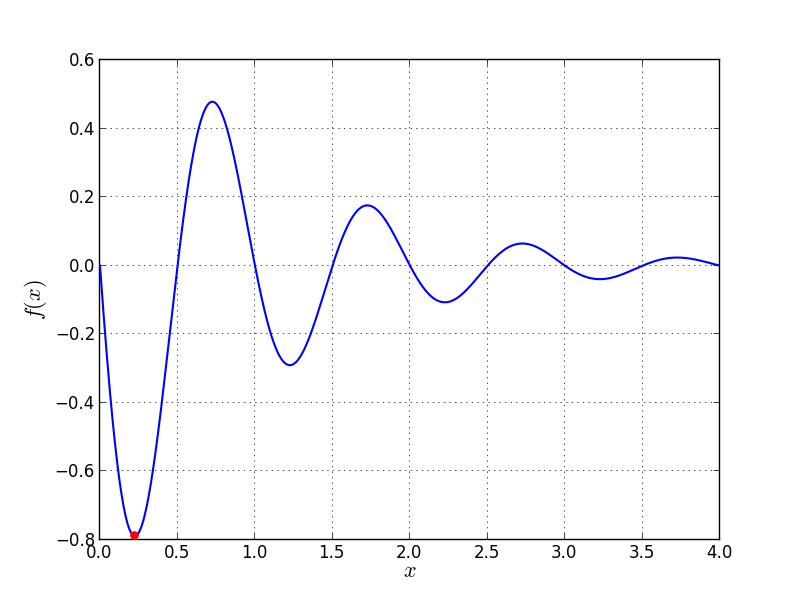
Univariate Problem14 function

Global optimum: 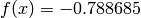$f(x)=-0.788685$ for $x = 0.224885$

class go_benchmark.Problem15(dimensions=1)¶

Univariate Problem15 test objective function.

This class defines the Univariate Problem15 global optimization problem. This is a multimodal minimization problem defined as follows:

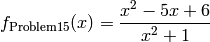
$f_{\text{Problem15}}(x) = \frac{x^{2} - 5 x + 6}{x^{2} + 1}$

Bound constraints: $x \in [-5, 5]$

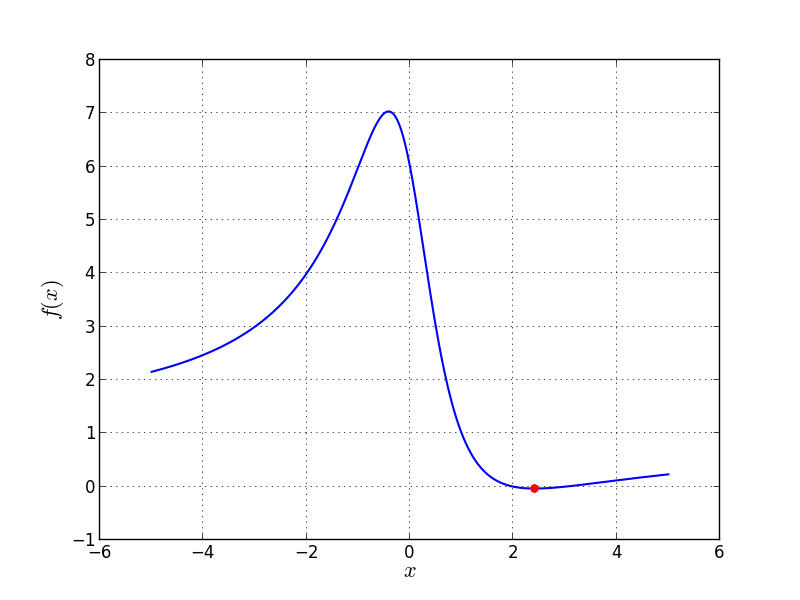
Univariate Problem15 function

Global optimum: $f(x)=-0.03553$ for $x = 2.41422$

class go_benchmark.Problem18(dimensions=1)¶

Univariate Problem18 test objective function.

This class defines the Univariate Problem18 global optimization problem. This is a multimodal minimization problem defined as follows:

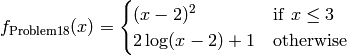
$f_{\text{Problem18}}(x) = \begin{cases}(x-2)^2 & \textrm{if} \hspace{5pt} x \leq 3 \\ 2\log(x-2)+1&\textrm{otherwise}\end{cases}$

Bound constraints: $x \in [0, 6]$

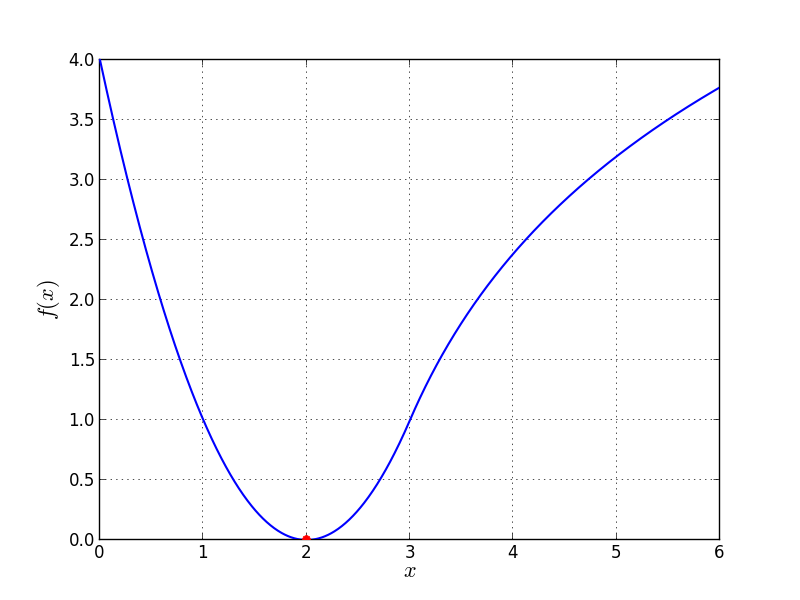
Univariate Problem18 function

Global optimum: $f(x)=0$ for $x = 2$

class go_benchmark.Problem20(dimensions=1)¶

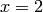
Univariate Problem20 test objective function.

This class defines the Univariate Problem20 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem20}}(x) = -[x-\sin(x)]e^{-x^2}$

Bound constraints: $x \in [-10, 10]$

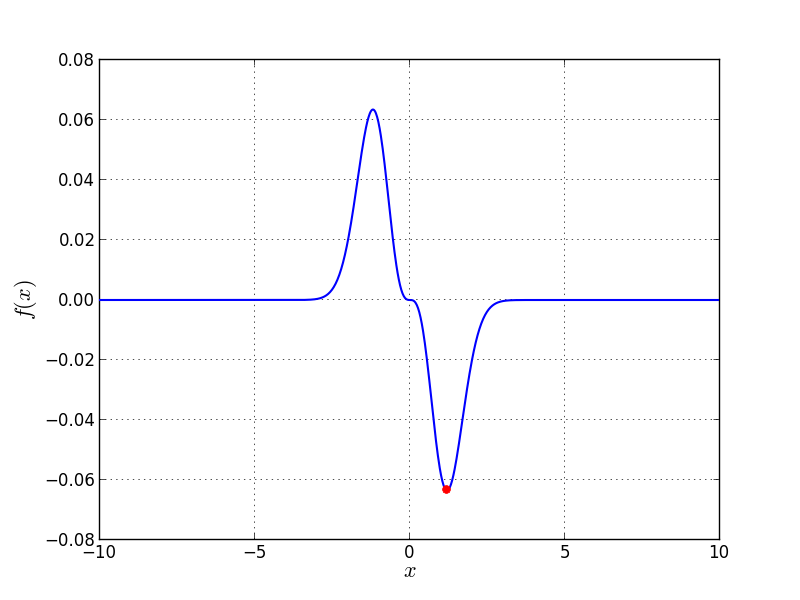
Univariate Problem20 function

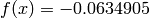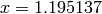
Global optimum: $f(x)=-0.0634905$ for $x = 1.195137$

class go_benchmark.Problem21(dimensions=1)¶

Univariate Problem21 test objective function.

This class defines the Univariate Problem21 global optimization problem. This is a multimodal minimization problem defined as follows:

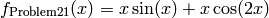
$f_{\text{Problem21}}(x) = x \sin(x) + x \cos(2x)$

Bound constraints: $x \in [0, 10]$

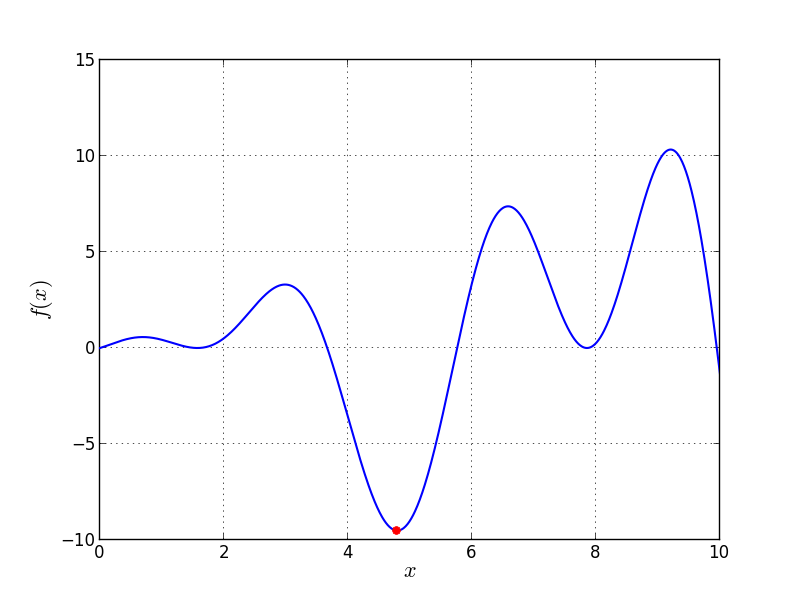
Univariate Problem21 function

Global optimum: $f(x)=-9.50835$ for $x = 4.79507$

class go_benchmark.Problem22(dimensions=1)¶

Univariate Problem22 test objective function.

This class defines the Univariate Problem22 global optimization problem. This is a multimodal minimization problem defined as follows:

$f_{\text{Problem22}}(x) = e^{-3x} - \sin^3(x)$

Bound constraints: $x \in [0, 20]$

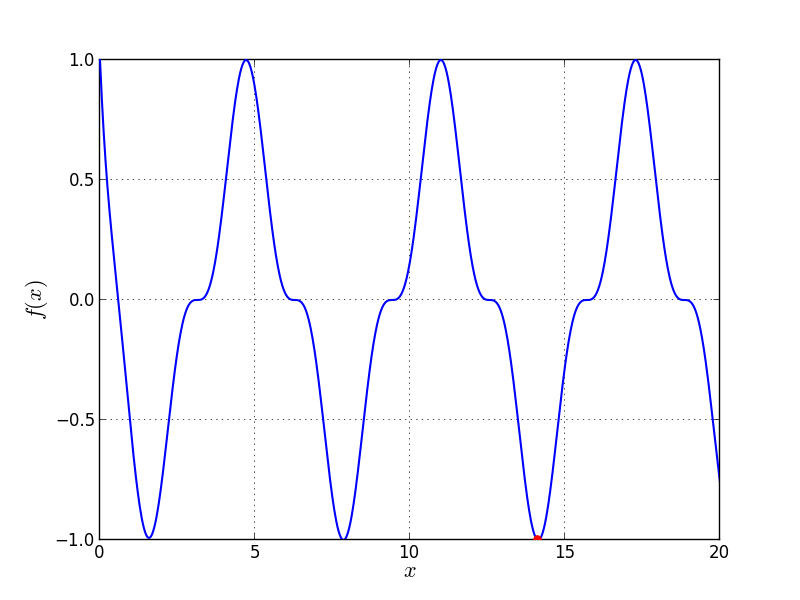
Univariate Problem22 function

Global optimum: 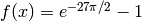$f(x)=e^{-27\pi/2} - 1$ for $x = 9\pi/2$

1-D Test Functions¶

Previous topic

This Page

Navigation

1-D Test Functions¶

Previous topic

This Page

Quick search

Navigation