 N-D Test Functions X¶
N-D Test Functions X¶Xin-She Yang 1 test objective function.
This class defines the Xin-She Yang 1 global optimization problem. This is a multimodal minimization problem defined as follows:
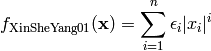
The variable 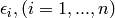 is a random variable uniformly distributed in
is a random variable uniformly distributed in ![[0, 1]](_images/math/ab178d831a786b92cb4c9ddc2d33578223036f98.png) .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
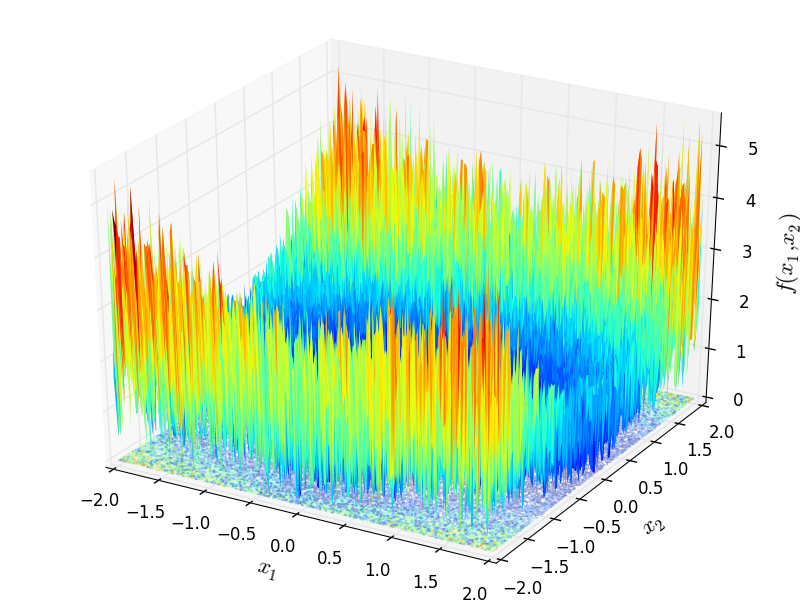
Two-dimensional Xin-She Yang 1 function
Global optimum:  for
for 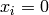 for
for 
Xin-She Yang 2 test objective function.
This class defines the Xin-She Yang 2 global optimization problem. This is a multimodal minimization problem defined as follows:
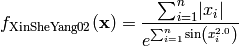
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-2\pi, 2\pi]](_images/math/550244574963351248b8b30f9d583095c065c220.png) for
for  .
.
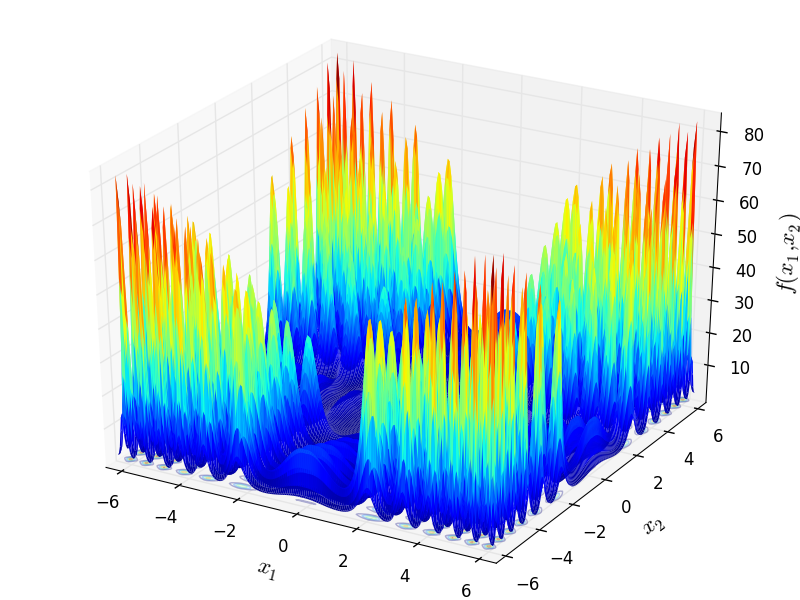
Two-dimensional Xin-She Yang 2 function
Global optimum:  for
for 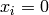 for
for 
Xin-She Yang 3 test objective function.
This class defines the Xin-She Yang 3 global optimization problem. This is a multimodal minimization problem defined as follows:
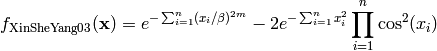
Where, in this exercise,  and
and 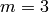 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-20, 20]](_images/math/026a917a812dbaef4e7a8ea87e9963bb111e2644.png) for
for  .
.
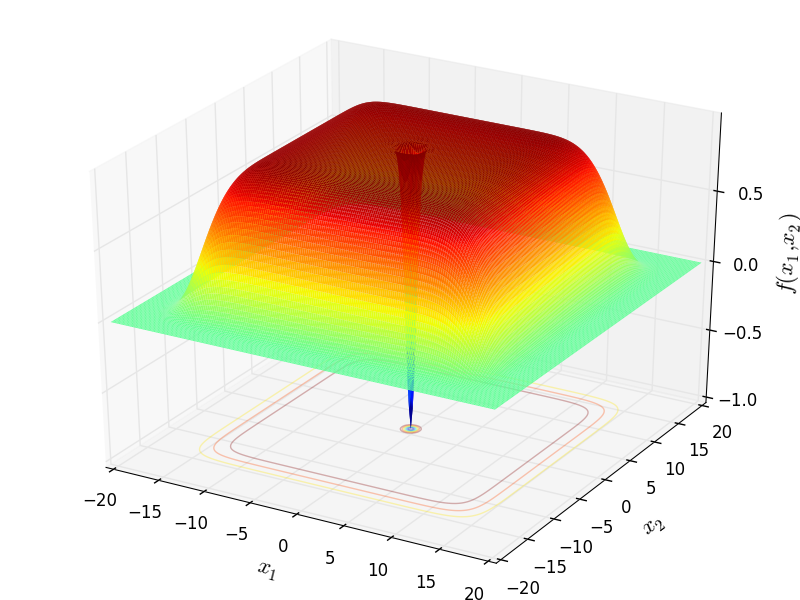
Two-dimensional Xin-She Yang 3 function
Global optimum:  for
for 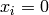 for
for 
Xin-She Yang 4 test objective function.
This class defines the Xin-She Yang 4 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{XinSheYang04}}(\mathbf{x}) = \left[ \sum_{i=1}^{n} \sin^2(x_i) - e^{-\sum_{i=1}^{n} x_i^2} \right ] e^{-\sum_{i=1}^{n} \sin^2 \sqrt{ \lvert x_i \rvert }}](_images/math/d385e33d9d3675ed690b61157e42afaaebe9c30e.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
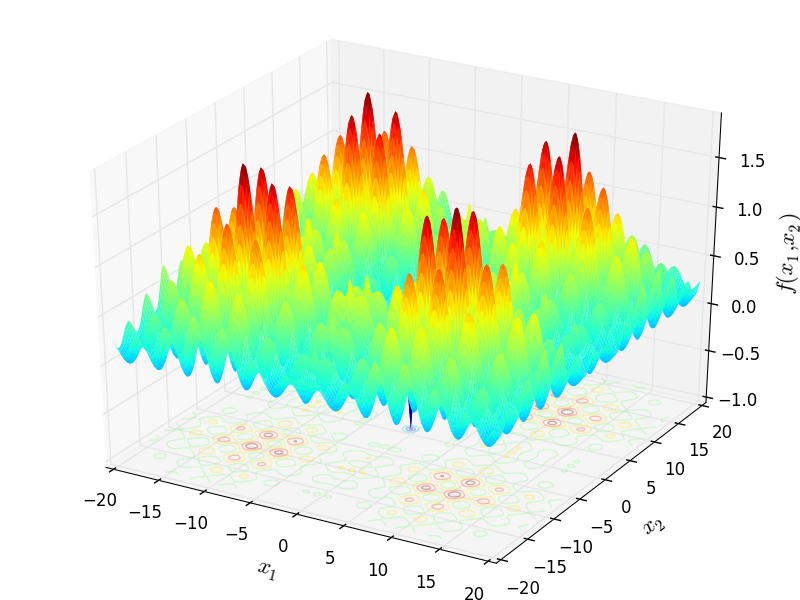
Two-dimensional Xin-She Yang 4 function
Global optimum:  for
for 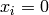 for
for 
Xor test objective function.
This class defines the Xor global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Xor}}(\mathbf{x}) = \left[ 1 + \exp \left( - \frac{x_7}{1 + \exp(-x_1 - x_2 - x_5)} - \frac{x_8}{1 + \exp(-x_3 - x_4 - x_6)} - x_9 \right ) \right ]^{-2} \\
+ \left [ 1 + \exp \left( -\frac{x_7}{1 + \exp(-x_5)} - \frac{x_8}{1 + \exp(-x_6)} - x_9 \right ) \right] ^{-2} \\
+ \left [1 - \left\{1 + \exp \left(-\frac{x_7}{1 + \exp(-x_1 - x_5)} - \frac{x_8}{1 + \exp(-x_3 - x_6)} - x_9 \right ) \right\}^{-1} \right ]^2 \\
+ \left [1 - \left\{1 + \exp \left(-\frac{x_7}{1 + \exp(-x_2 - x_5)} - \frac{x_8}{1 + \exp(-x_4 - x_6)} - x_9 \right ) \right\}^{-1} \right ]^2](_images/math/879799c74892110b6eb0ea520c7572c4ad7c4f33.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
Global optimum: 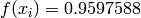 for
for ![\mathbf{x} = [1, -1, 1, -1, -1, 1, 1, -1, 0.421134]](_images/math/fb03fa96628e4c5633f6527b9625fec9246a7088.png)