 N-D Test Functions W¶
N-D Test Functions W¶Watson test objective function.
This class defines the Watson global optimization problem. This is a unimodal minimization problem defined as follows:
![f_{\text{Watson}}(\mathbf{x}) = \sum_{i=0}^{29} \left\{ \sum_{j=0}^4 ((j - 1)a_i^j x_{j+1}) - \left[ \sum_{j=0}^5 a_i^j x_{j+1} \right ]^2 - 1 \right\}^2 + x_1^2](_images/math/edda0287e0c3d161d02e25b729864e98e402439b.png)
Where, in this exercise, 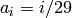 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for 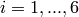 .
.
Global optimum: 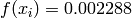 for
for ![\mathbf{x} = [-0.0158, 1.012, -0.2329, 1.260, -1.513, 0.9928]](_images/math/6b3586c898a22817ad72e0f2f2d622c342ad67bd.png)
W / Wavy test objective function.
This class defines the W / Wavy global optimization problem. This is a multimodal minimization problem defined as follows:

Where, in this exercise, 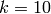 . The number of local minima is
. The number of local minima is  and
and  for odd and even
for odd and even  respectively.
respectively.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-\pi, \pi]](_images/math/f3c18fa54f78b0fbb91f6c094697293de5e0b3f9.png) for
for  .
.
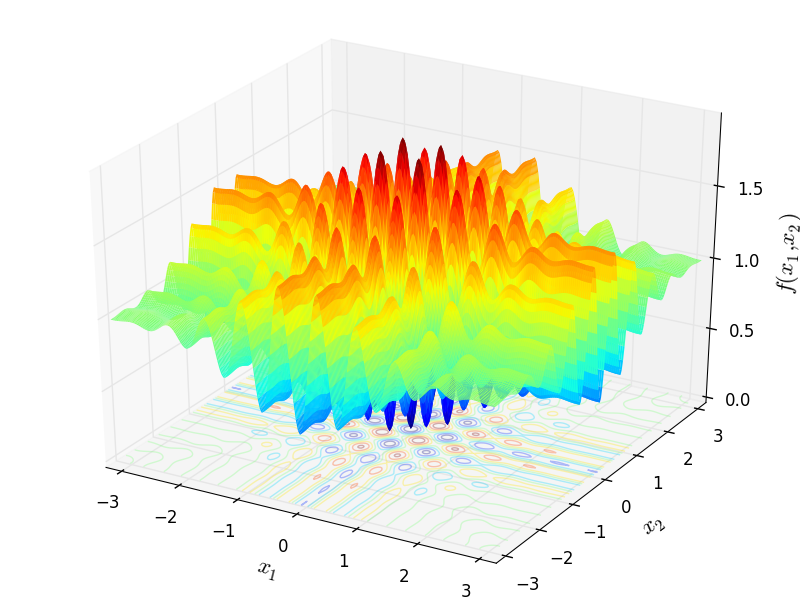
Two-dimensional W / Wavy function
Global optimum:  for
for  for
for 
Wayburn and Seader 1 test objective function.
This class defines the Wayburn and Seader 1 global optimization problem. This is a unimodal minimization problem defined as follows:
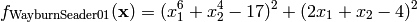
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
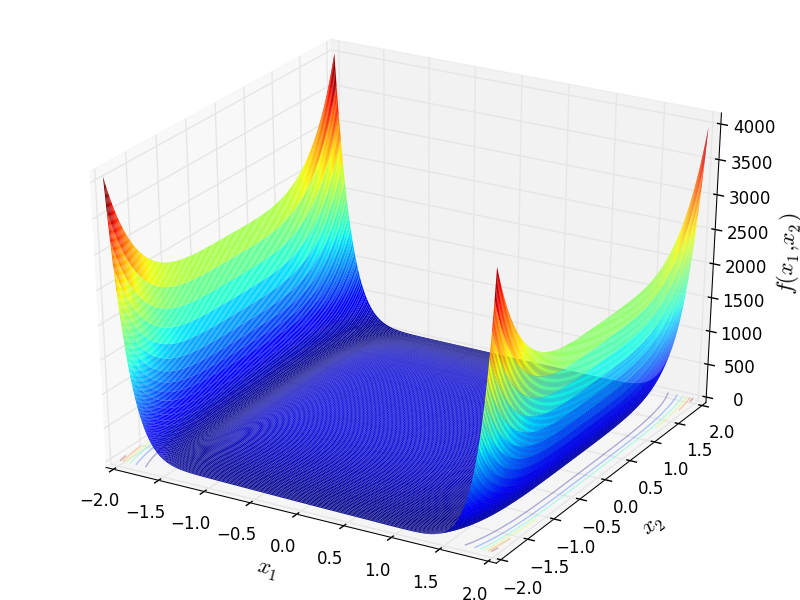
Two-dimensional Wayburn and Seader 1 function
Global optimum:  for
for ![\mathbf{x} = [1, 2]](_images/math/f293ed6d993e1d9892bced5d4f409f0a74cc40d6.png)
Wayburn and Seader 2 test objective function.
This class defines the Wayburn and Seader 2 global optimization problem. This is a unimodal minimization problem defined as follows:
![f_{\text{WayburnSeader02}}(\mathbf{x}) = \left[ 1.613 - 4(x_1 - 0.3125)^2 - 4(x_2 - 1.625)^2 \right]^2 + (x_2 - 1)^2](_images/math/990be194ff5d87d2b15fec0893a170bfa5677b3b.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
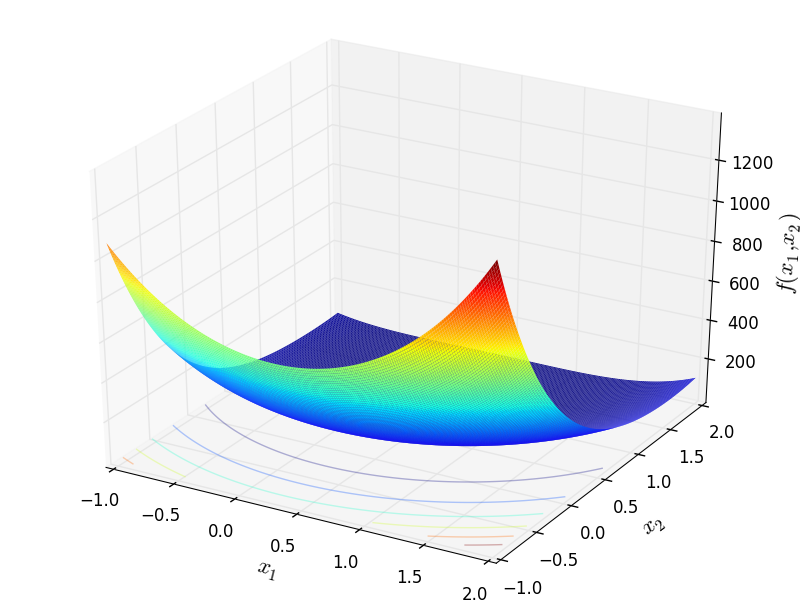
Two-dimensional Wayburn and Seader 2 function
Global optimum:  for
for ![\mathbf{x} = [0.2, 1]](_images/math/b117022a43083e1f1edb1fca27f3200db815b2b9.png)
Weierstrass test objective function.
This class defines the Weierstrass global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Weierstrass}}(\mathbf{x}) = \sum_{i=1}^{n} \left [ \sum_{k=0}^{kmax} a^k \cos \left( 2 \pi b^k (x_i + 0.5) \right) - n \sum_{k=0}^{kmax} a^k \cos(\pi b^k) \right ]](_images/math/1bc139bde96f08a1d941759e448b88a68a7369aa.png)
Where, in this exercise, 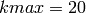 ,
, 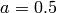 and
and 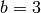 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-0.5, 0.5]](_images/math/95ff94da73788fc2234f6d2f9037e3c7df81a147.png) for
for  .
.
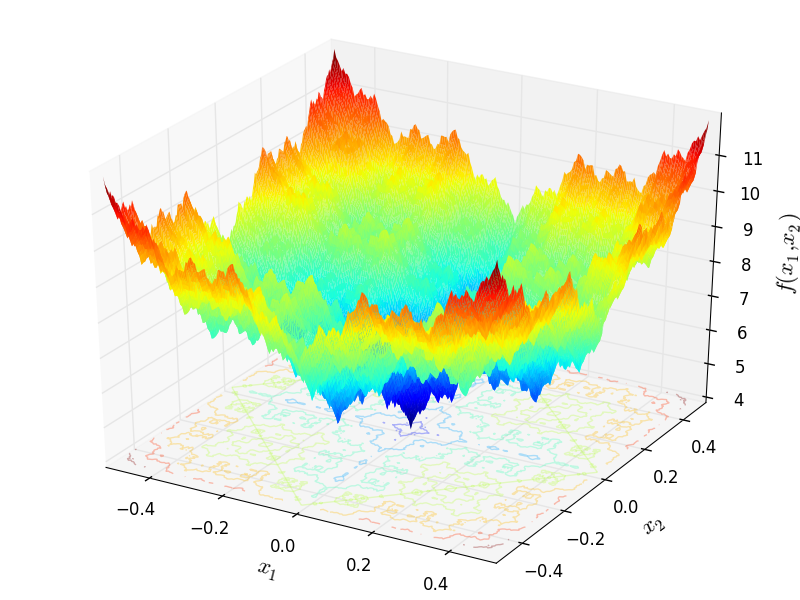
Two-dimensional Weierstrass function
Global optimum: 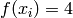 for
for  for
for 
Whitley test objective function.
This class defines the Whitley global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Whitley}}(\mathbf{x}) = \sum_{i=1}^n \sum_{j=1}^n \left[\frac{(100(x_i^2-x_j)^2 + (1-x_j)^2)^2}{4000} - \cos(100(x_i^2-x_j)^2 + (1-x_j)^2)+1 \right]](_images/math/547f15968bc97fb68942a1bdc08dca77ed2687cd.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10.24, 10.24]](_images/math/3825846d98928e737251a1183cf6de356b0abc81.png) for
for  .
.
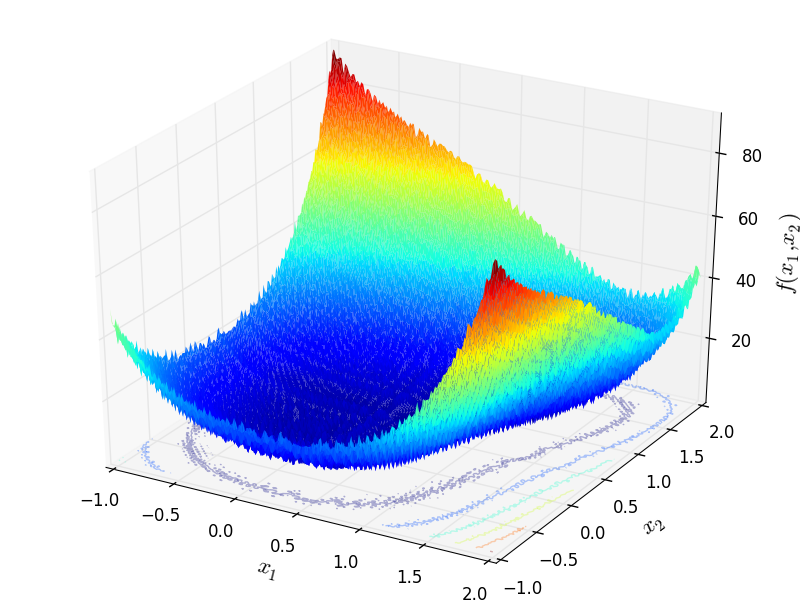
Two-dimensional Whitley function
Global optimum:  for
for 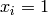 for
for 
Wolfe test objective function.
This class defines the Wolfe global optimization problem. This is a multimodal minimization problem defined as follows:
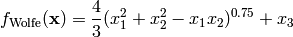
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 2]](_images/math/4ccbc8f05068478e57d7a9f37fccf74917eabaae.png) for
for  .
.
Global optimum:  for
for  for
for 