 N-D Test Functions T¶
N-D Test Functions T¶TestTubeHolder test objective function.
This class defines the TestTubeHolder global optimization problem. This is a multimodal minimization problem defined as follows:
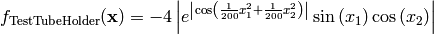
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
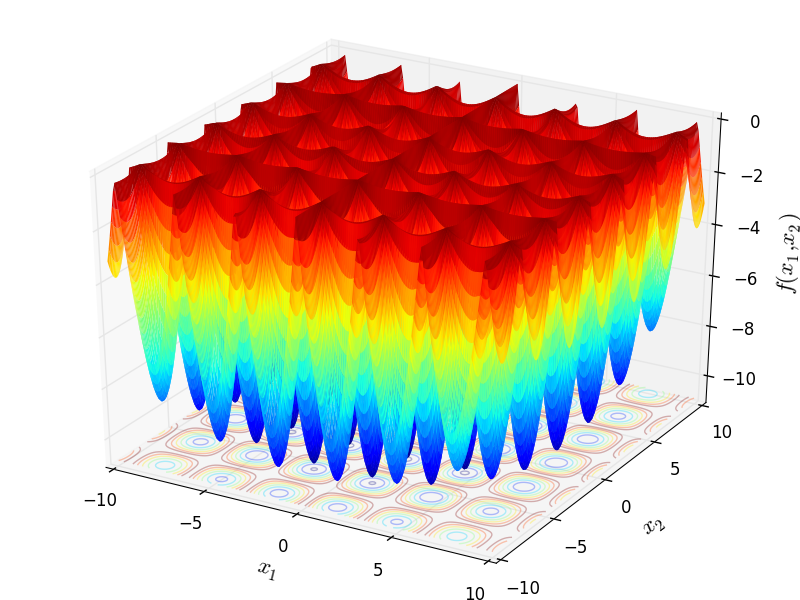
Two-dimensional TestTubeHolder function
Global optimum: 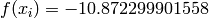 for
for ![\mathbf{x} = [-\pi/2, 0]](_images/math/c6df4d194285bc20454f67e0b6f3878577706aef.png)
Three Hump Camel test objective function.
This class defines the Three Hump Camel global optimization problem. This is a multimodal minimization problem defined as follows:
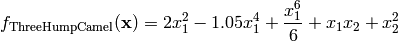
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
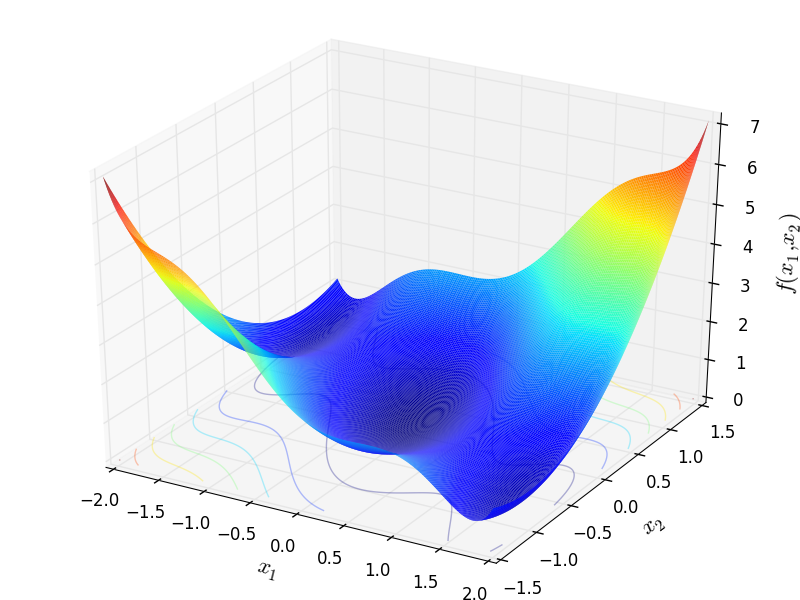
Two-dimensional Three Hump Camel function
Global optimum:  for
for ![\mathbf{x} = [0, 0]](_images/math/ae446016118c18b04012af8feda9cc5e2e1808a6.png)
Treccani test objective function.
This class defines the Treccani global optimization problem. This is a multimodal minimization problem defined as follows:
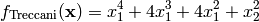
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
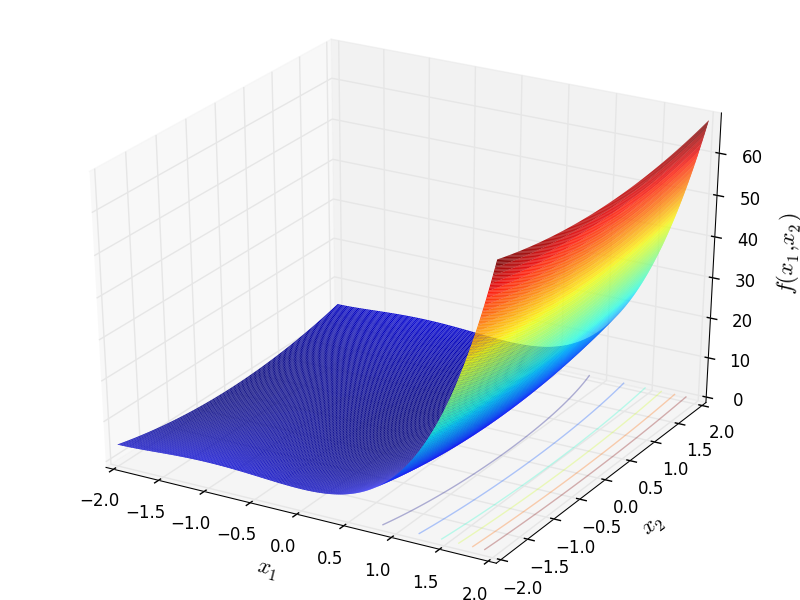
Two-dimensional Treccani function
Global optimum:  for
for ![\mathbf{x} = [-2, 0]](_images/math/19935f158a37040f2bd69fae014ba4ad2ee35b5b.png) or
or ![\mathbf{x} = [0, 0]](_images/math/ae446016118c18b04012af8feda9cc5e2e1808a6.png) .
.
Trefethen test objective function.
This class defines the Trefethen global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trefethen}}(\mathbf{x}) = 0.25 x_{1}^{2} + 0.25 x_{2}^{2} + e^{\sin\left(50 x_{1}\right)} - \sin\left(10 x_{1} + 10 x_{2}\right) + \sin\left(60 e^{x_{2}}\right) + \sin\left[70 \sin\left(x_{1}\right)\right] + \sin\left[\sin\left(80 x_{2}\right)\right]](_images/math/3e1ba592e7148b2a821fb50587a84e56739d9e6a.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
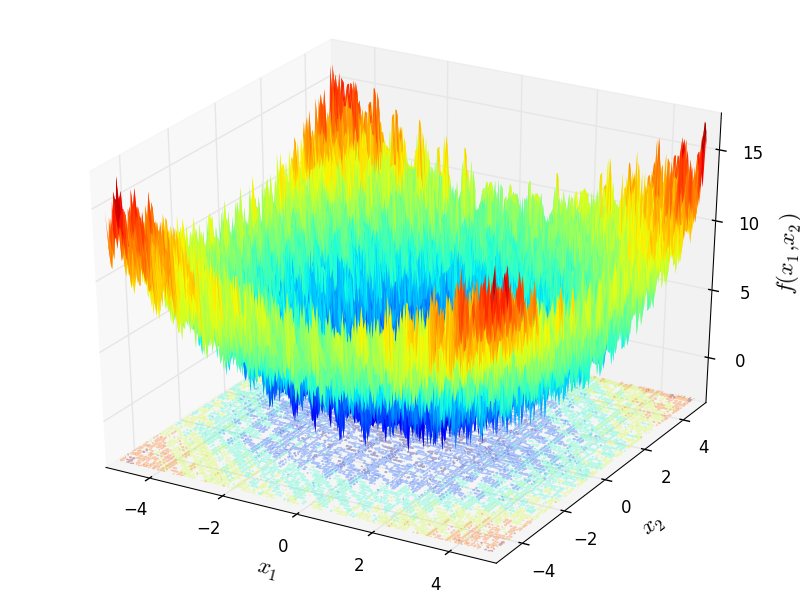
Two-dimensional Trefethen function
Global optimum: 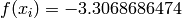 for
for ![\mathbf{x} = [-0.02440307923, 0.2106124261]](_images/math/5106486a79f632c5c8c97a2f545c77ff65c6d696.png)
Trid test objective function.
This class defines the Trid global optimization problem. This is a multimodal minimization problem defined as follows:
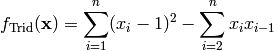
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-20, 20]](_images/math/026a917a812dbaef4e7a8ea87e9963bb111e2644.png) for
for 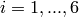 .
.
Global optimum:  for
for ![\mathbf{x} = [6, 10, 12, 12, 10, 6]](_images/math/0c89c713f8368e274f7dd77459f2159c71cbb800.png)
Trigonometric 1 test objective function.
This class defines the Trigonometric 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trigonometric01}}(\mathbf{x}) = \sum_{i=1}^{n} \left [n - \sum_{j=1}^{n} \cos(x_j) + i \left(1 - cos(x_i) - sin(x_i) \right ) \right]^2](_images/math/c8b9de6db168064494fefe6e758d533b3f44de0f.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, \pi]](_images/math/10b9f829ecf73e20ecc5c80159a1d1615d4c0f6a.png) for
for  .
.
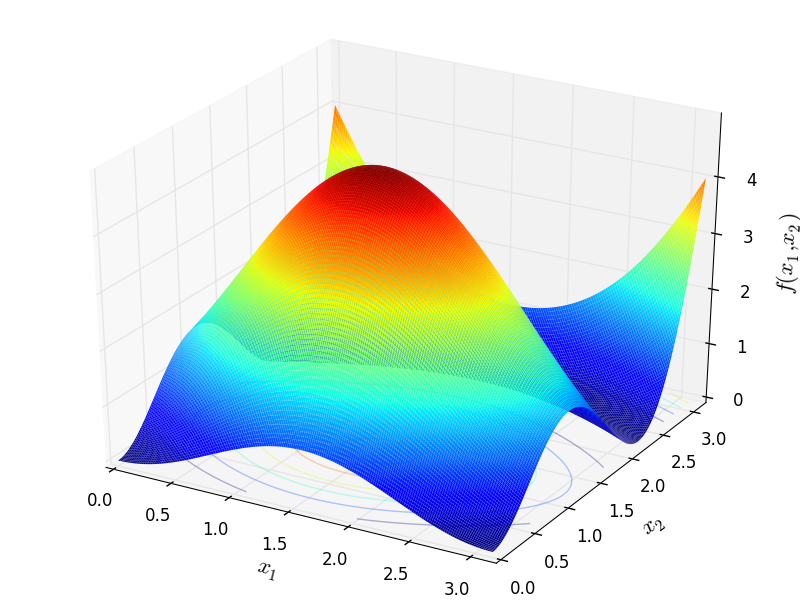
Two-dimensional Trigonometric 1 function
Global optimum:  for
for 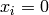 for
for 
Trigonometric 2 test objective function.
This class defines the Trigonometric 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Trigonometric2}}(\mathbf{x}) = 1 + \sum_{i=1}^{n} 8 \sin^2 \left[7(x_i - 0.9)^2 \right] + 6 \sin^2 \left[14(x_i - 0.9)^2 \right] + (x_i - 0.9)^2](_images/math/d2025c8a506a9de3136a245ccd213d324c53a3e9.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
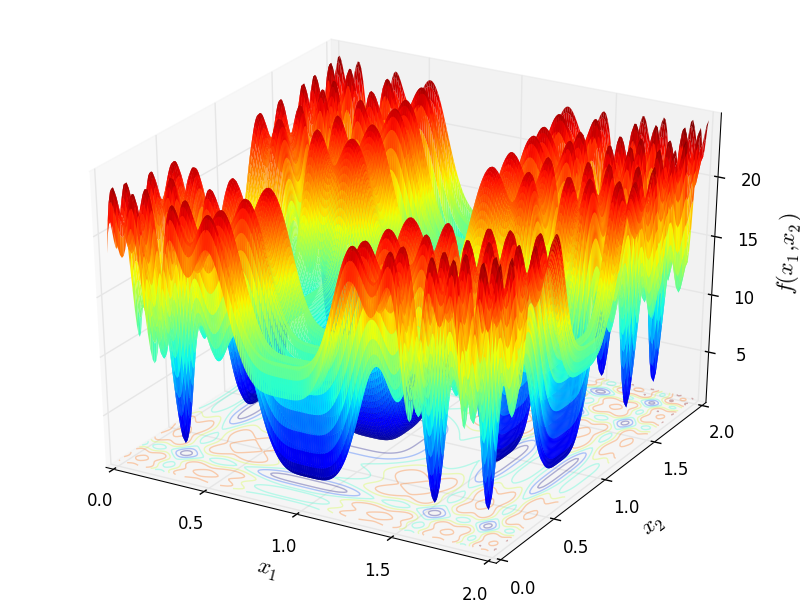
Two-dimensional Trigonometric 2 function
Global optimum: 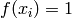 for
for  for
for 
Tripod test objective function.
This class defines the Tripod global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Tripod}}(\mathbf{x}) = p(x_2) \left[1 + p(x_1) \right] + \lvert x_1 + 50p(x_2) \left[1 - 2p(x_1) \right] \rvert + \lvert x_2 + 50\left[1 - 2p(x_2)\right] \rvert](_images/math/9f4ca084ab0d5639837d18bec8d265086dc0f3cc.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
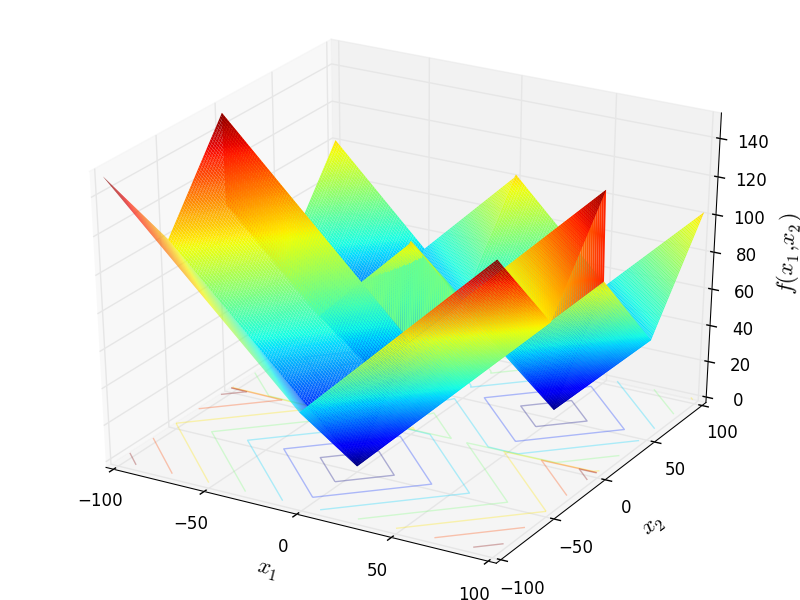
Two-dimensional Tripod function
Global optimum:  for
for ![\mathbf{x} = [0, -50]](_images/math/a96ff3f15af07d31c3edd8043735a485578fed61.png)