 N-D Test Functions S¶
N-D Test Functions S¶Salomon test objective function.
This class defines the Salomon global optimization problem. This is a multimodal minimization problem defined as follows:
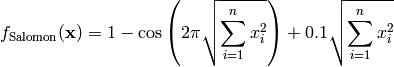
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
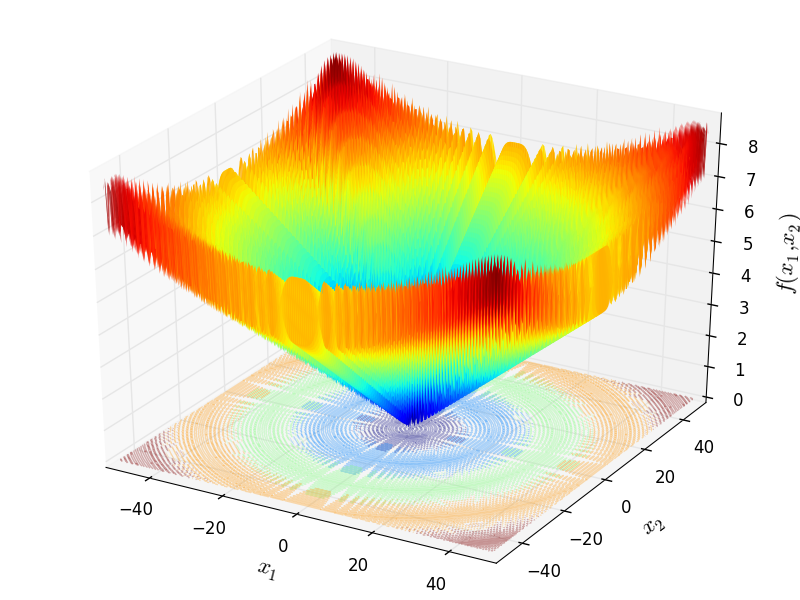
Two-dimensional Salomon function
Global optimum:  for
for  for
for 
Sargan test objective function.
This class defines the Sargan global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
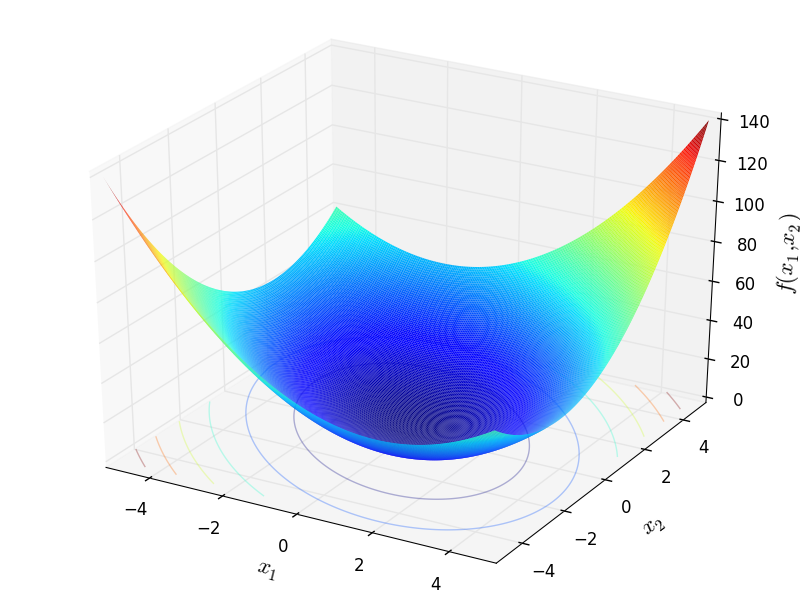
Two-dimensional Sargan function
Global optimum:  for
for  for
for 
Schaffer 1 test objective function.
This class defines the Schaffer 1 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
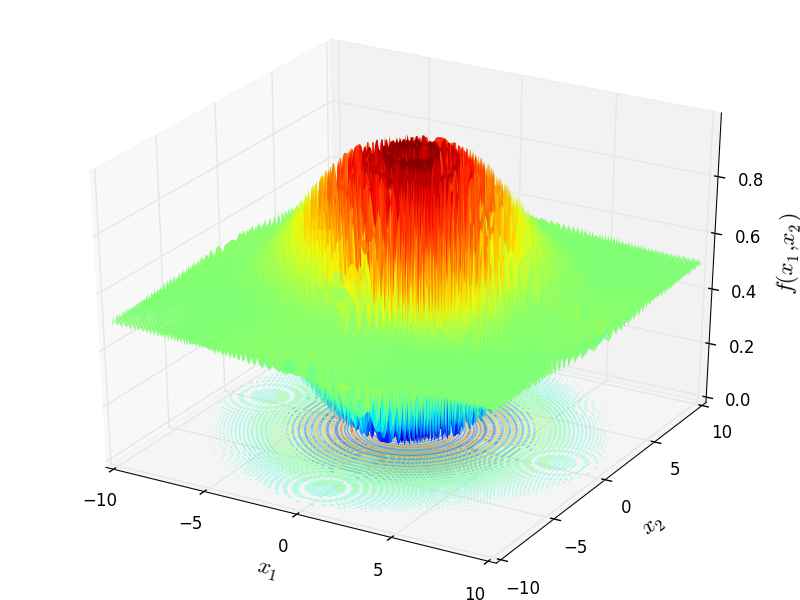
Two-dimensional Schaffer 1 function
Global optimum:  for
for  for
for 
Schaffer 2 test objective function.
This class defines the Schaffer 2 global optimization problem. This is a multimodal minimization problem defined as follows:
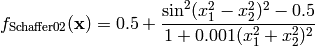
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
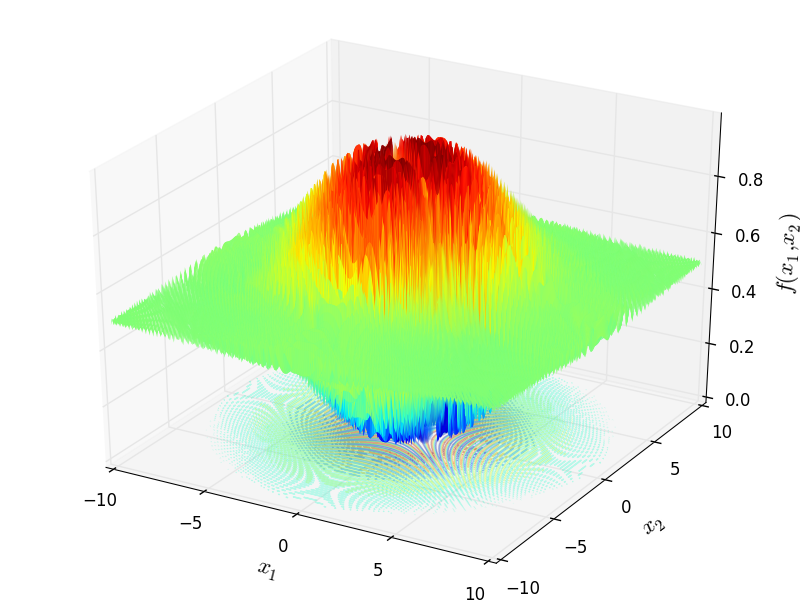
Two-dimensional Schaffer 2 function
Global optimum:  for
for  for
for 
Schaffer 3 test objective function.
This class defines the Schaffer 3 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
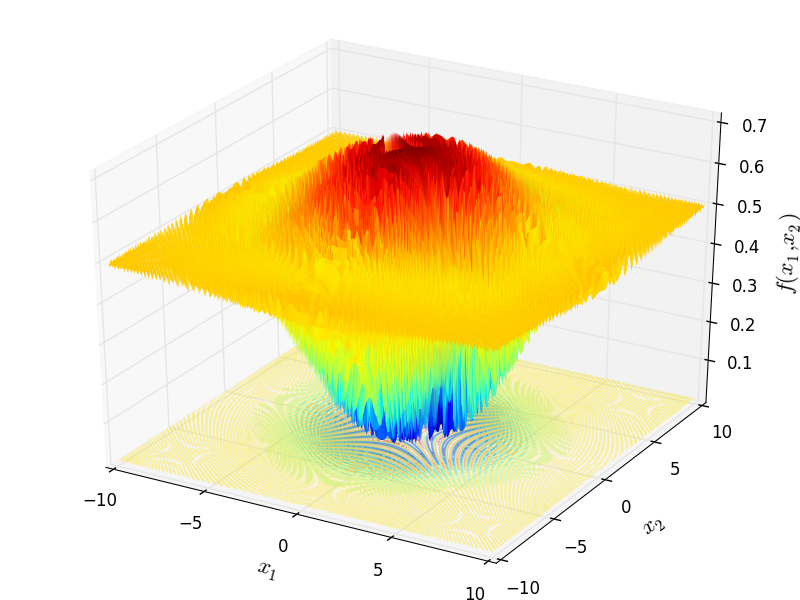
Two-dimensional Schaffer 3 function
Global optimum: 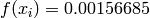 for
for ![\mathbf{x} = [0, 1.253115]](_images/math/1c8a14ce656a36907bd498cf922a1648d19c2e1d.png)
Schaffer 4 test objective function.
This class defines the Schaffer 4 global optimization problem. This is a multimodal minimization problem defined as follows:
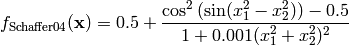
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
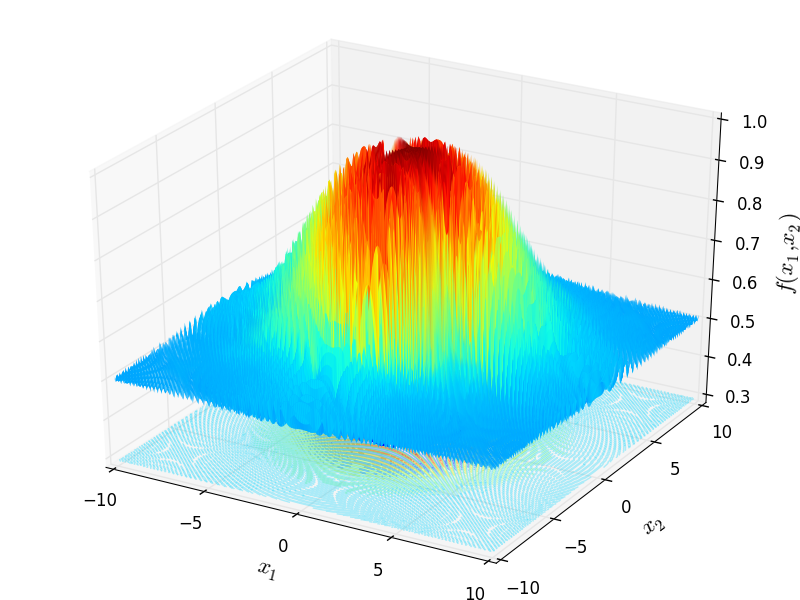
Two-dimensional Schaffer 4 function
Global optimum: 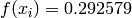 for
for ![\mathbf{x} = [0, 1.253115]](_images/math/1c8a14ce656a36907bd498cf922a1648d19c2e1d.png)
Schmidt-Vetters test objective function.
This class defines the Schmidt-Vetters global optimization problem. This is a multimodal minimization problem defined as follows:
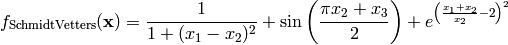
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
Global optimum: 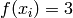 for
for 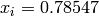 for
for 
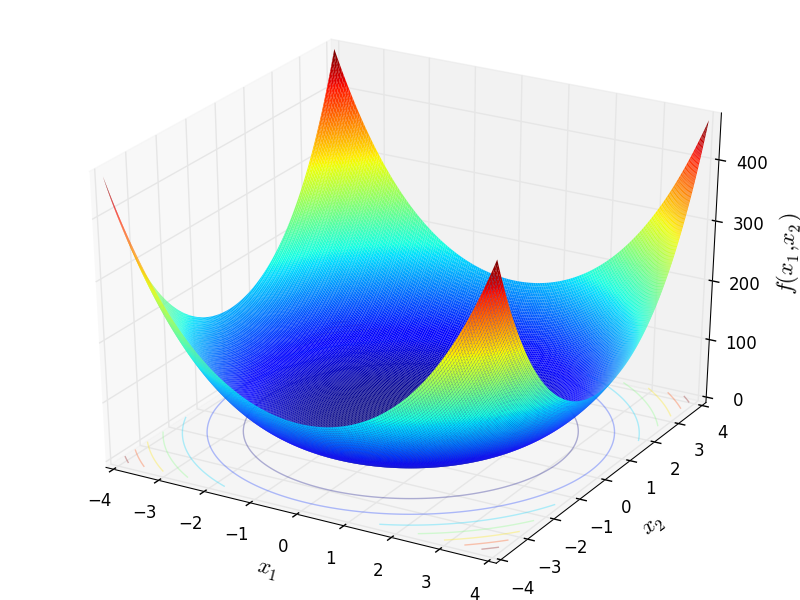
Schwefel 1 test objective function.
This class defines the Schwefel 1 global optimization problem. This is a unimodal minimization problem defined as follows:
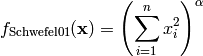
Where, in this exercise, 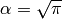 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
Two-dimensional Schwefel 1 function
Global optimum:  for
for  for
for 
Schwefel 2 test objective function.
This class defines the Schwefel 2 global optimization problem. This is a unimodal minimization problem defined as follows:
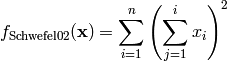
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
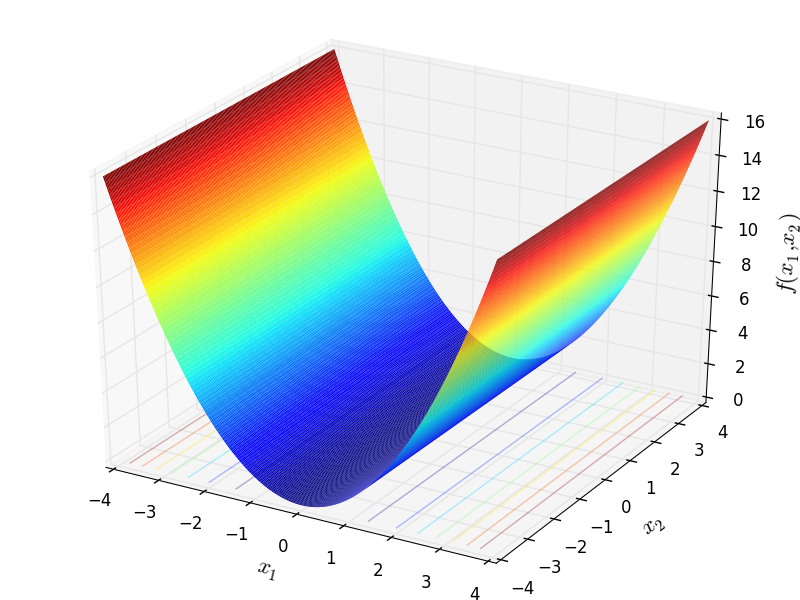
Two-dimensional Schwefel 2 function
Global optimum:  for
for  for
for 
Schwefel 4 test objective function.
This class defines the Schwefel 4 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Schwefel04}}(\mathbf{x}) = \sum_{i=1}^n \left[(x_i - 1)^2 + (x_1 - x_i^2)^2 \right]](_images/math/91ce2f09edc56fecc35a1e898ef7c68bdc3ec675.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
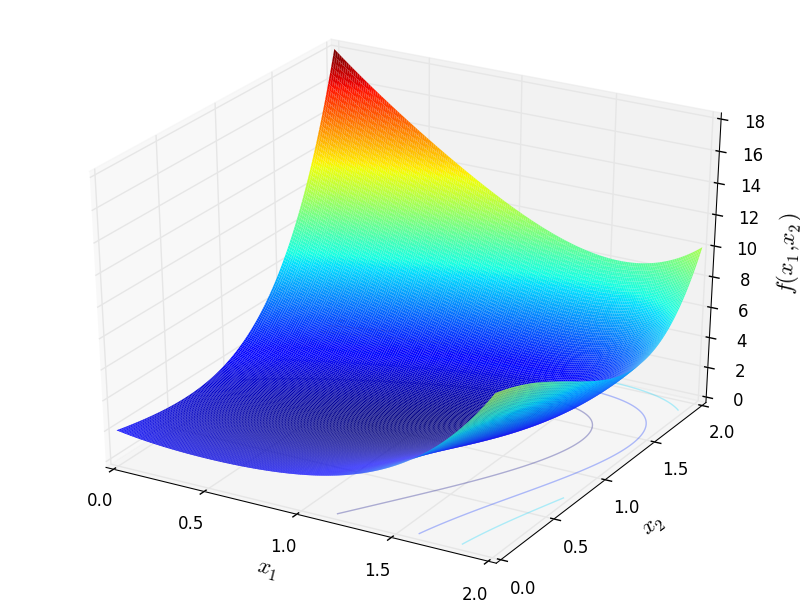
Two-dimensional Schwefel 4 function
Global optimum:  for
for 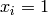 for
for 
Schwefel 6 test objective function.
This class defines the Schwefel 6 global optimization problem. This is a unimodal minimization problem defined as follows:
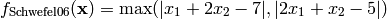
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
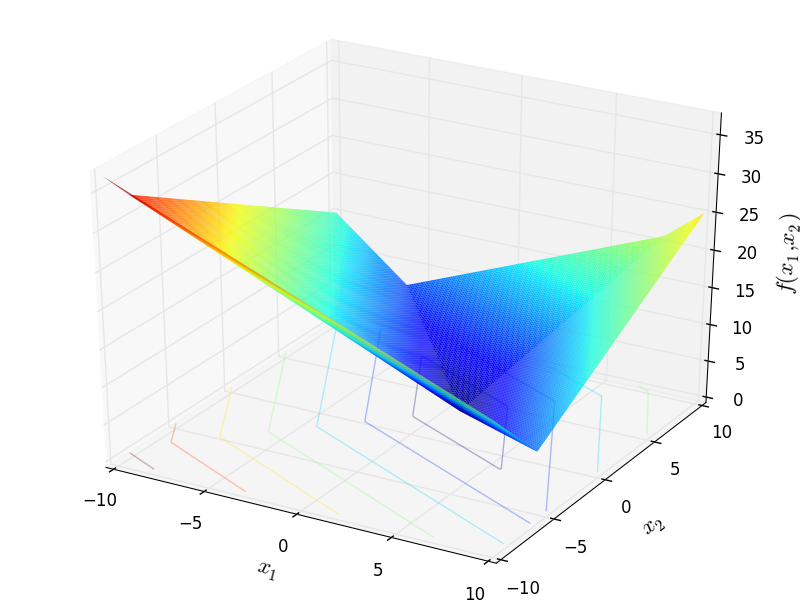
Two-dimensional Schwefel 6 function
Global optimum:  for
for ![\mathbf{x} = [1, 3]](_images/math/e85719292cf919a07142ed7f6c9f792d75bf0332.png)
Schwefel 20 test objective function.
This class defines the Schwefel 20 global optimization problem. This is a unimodal minimization problem defined as follows:
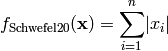
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
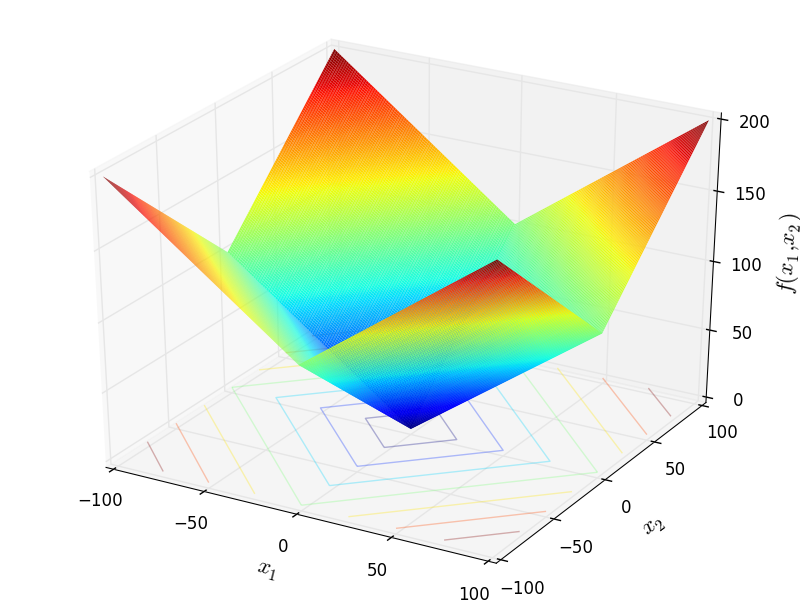
Two-dimensional Schwefel 20 function
Global optimum:  for
for  for
for 
Schwefel 21 test objective function.
This class defines the Schwefel 21 global optimization problem. This is a unimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
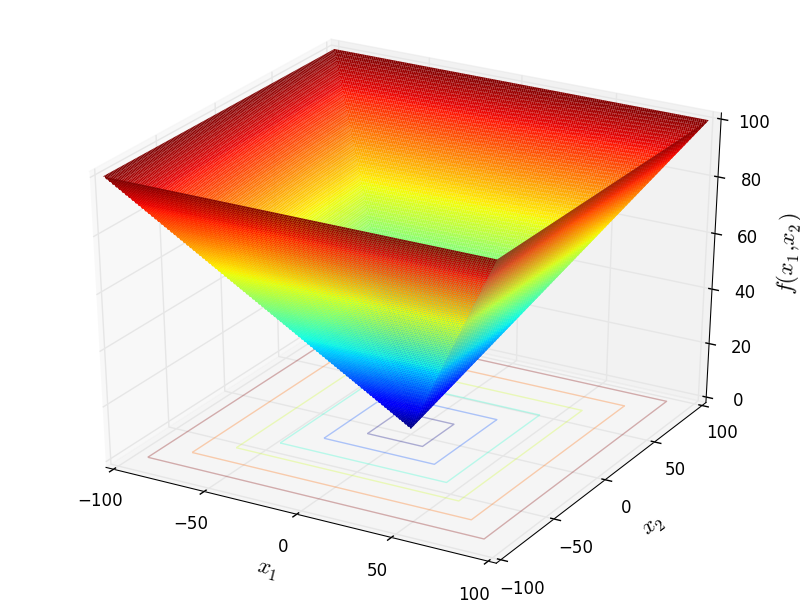
Two-dimensional Schwefel 21 function
Global optimum:  for
for  for
for 
Schwefel 22 test objective function.
This class defines the Schwefel 22 global optimization problem. This is a multimodal minimization problem defined as follows:
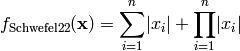
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
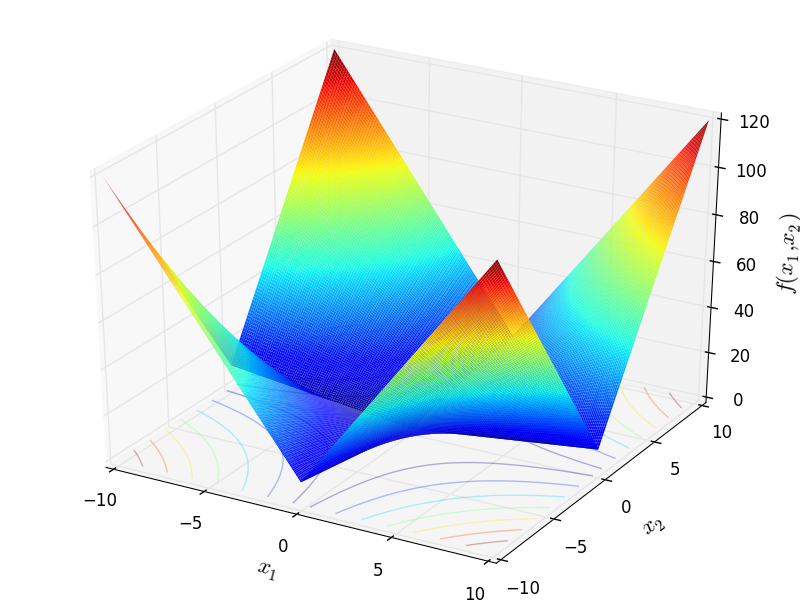
Two-dimensional Schwefel 22 function
Global optimum:  for
for  for
for 
Schwefel 26 test objective function.
This class defines the Schwefel 26 global optimization problem. This is a multimodal minimization problem defined as follows:
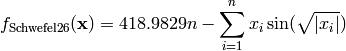
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
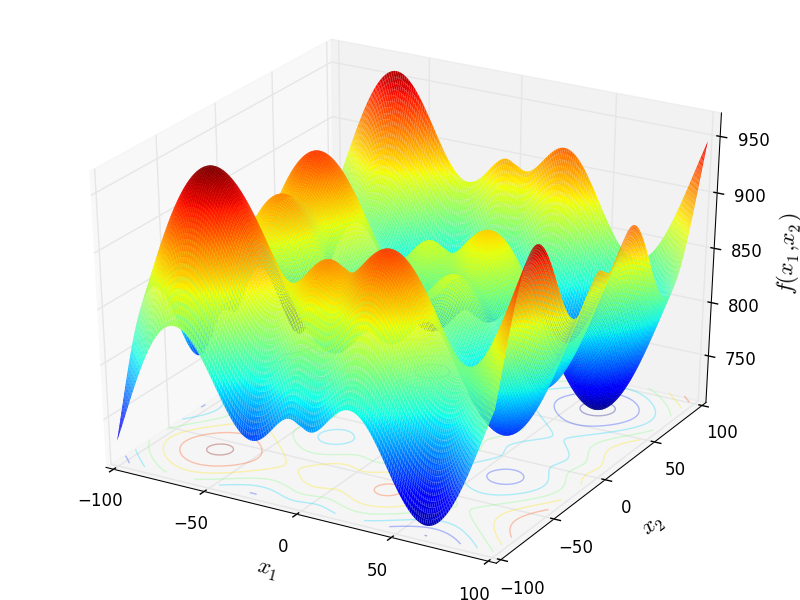
Two-dimensional Schwefel 26 function
Global optimum:  for
for 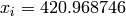 for
for 
Schwefel 36 test objective function.
This class defines the Schwefel 36 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 500]](_images/math/da5613ad206e6bb117f3e6258874921cda1ab408.png) for
for  .
.
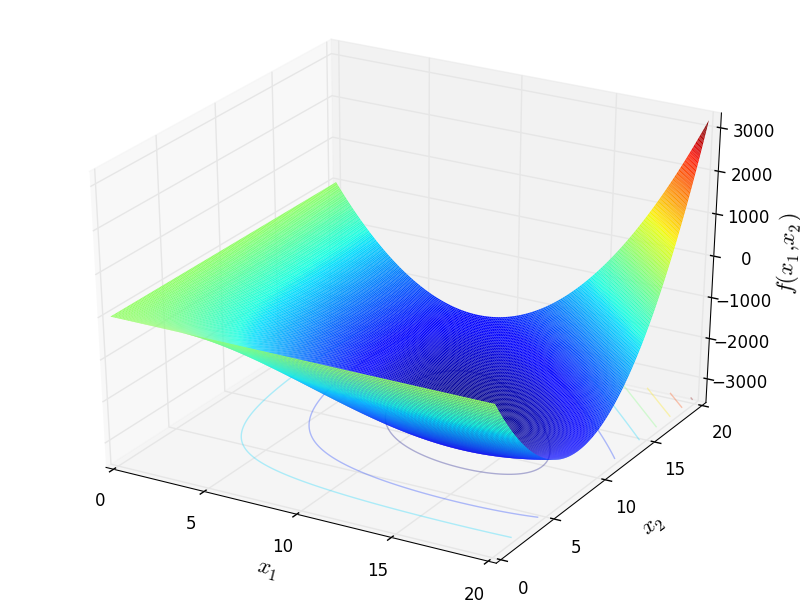
Two-dimensional Schwefel 36 function
Global optimum: 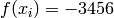 for
for ![\mathbf{x} = [12, 12]](_images/math/8d6e171f9eb00c762e5603ec8859d8832d2b87ce.png)
Shekel 5 test objective function.
This class defines the Shekel 5 global optimization problem. This is a multimodal minimization problem defined as follows:
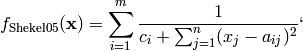
Where, in this exercise:
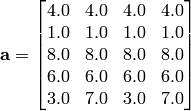
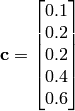
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
Global optimum: 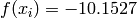 for
for 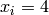 for
for 
Shekel 7 test objective function.
This class defines the Shekel 7 global optimization problem. This is a multimodal minimization problem defined as follows:
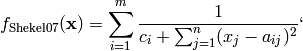
Where, in this exercise:


Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
Global optimum:  for
for 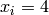 for
for 
Shekel 10 test objective function.
This class defines the Shekel 10 global optimization problem. This is a multimodal minimization problem defined as follows:

Where, in this exercise:
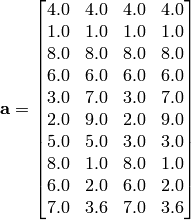
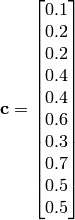
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
Global optimum: 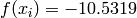 for
for 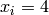 for
for 
Shubert 1 test objective function.
This class defines the Shubert 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Shubert01}}(\mathbf{x}) = \left( \sum\limits_{i=1}^{5} i\cos[(i+1)x_1 + i] \right) \left( \sum\limits_{i=1}^{5} i\cos[(i+1)x_2 + i] \right)](_images/math/80ae0f9fb9c27d62eadc11e6ce07d89f7df6c063.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
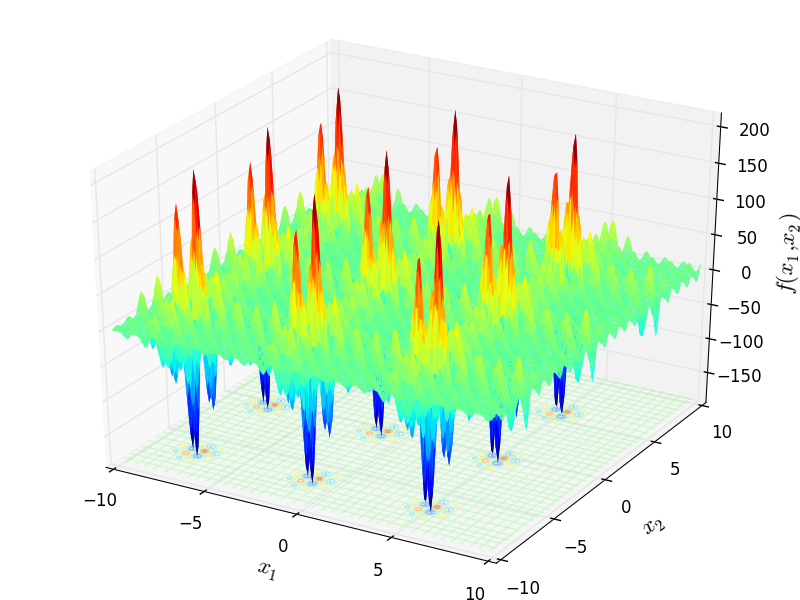
Two-dimensional Shubert 1 function
Global optimum: 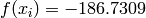 for
for ![\mathbf{x} = [-7.0835, 4.8580]](_images/math/d5178982baf69ca618ab7f014c82596a8606495a.png) (and many others).
(and many others).
Shubert 3 test objective function.
This class defines the Shubert 3 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Shubert03}}(\mathbf{x}) = \sum_{i=1}^n \sum_{j=1}^5 j \sin \left[(j+1)x_i \right] + j](_images/math/96157286b6961f80a8a3dfde86ade1830dc7017b.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
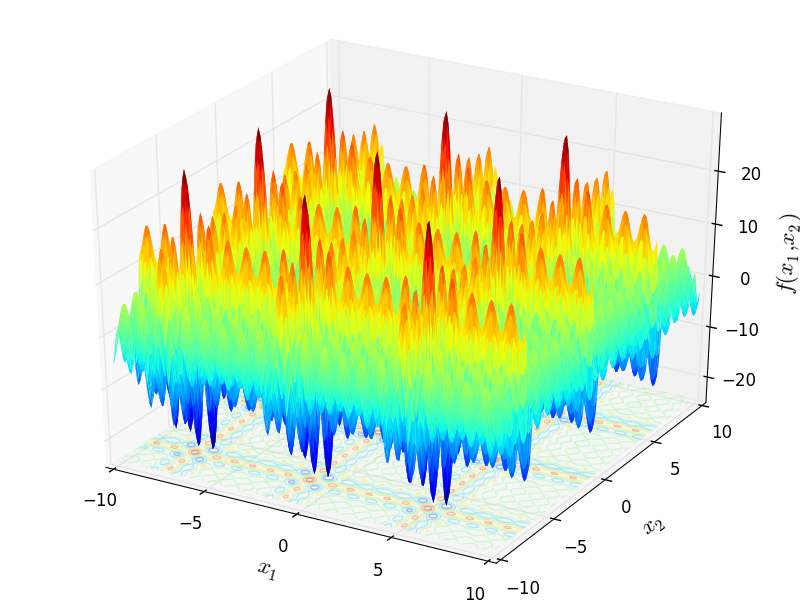
Two-dimensional Shubert 3 function
Global optimum: 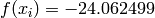 for
for ![\mathbf{x} = [5.791794, 5.791794]](_images/math/5e68533377e3724168910c9274c978a7943f7b85.png) (and many others).
(and many others).
Shubert 4 test objective function.
This class defines the Shubert 4 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Shubert04}}(\mathbf{x}) = \sum_{i=1}^n \sum_{j=1}^5 j \cos \left[(j+1)x_i \right] + j](_images/math/d38beee1312c3afe303b90bd1c06cefdb6bd55c0.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
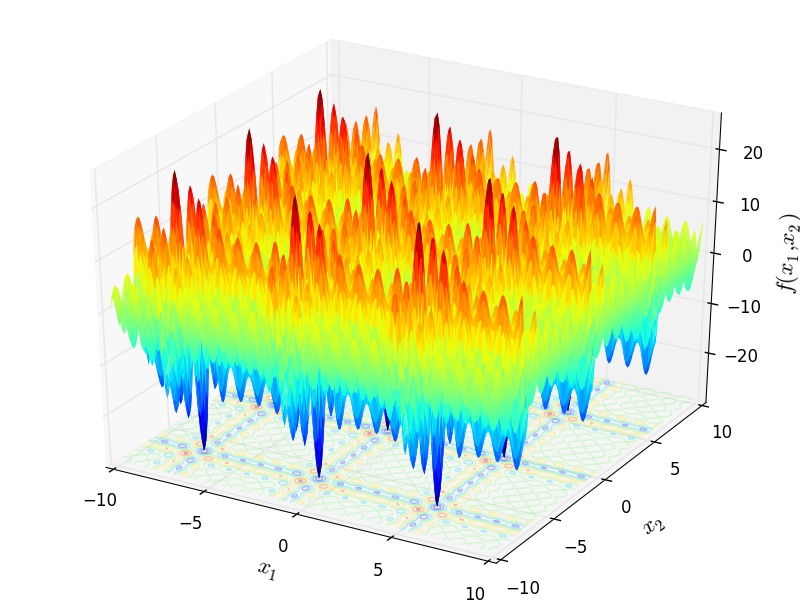
Two-dimensional Shubert 4 function
Global optimum: 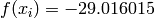 for
for ![\mathbf{x} = [-0.80032121, -7.08350592]](_images/math/71dcb497d4fc2d394b1b5eb04ef5856569989a99.png) (and many others).
(and many others).
SineEnvelope test objective function.
This class defines the SineEnvelope global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{SineEnvelope}}(\mathbf{x}) = -\sum_{i=1}^{n-1}\left[\frac{\sin^2(\sqrt{x_{i+1}^2+x_{i}^2}-0.5)}{(0.001(x_{i+1}^2+x_{i}^2)+1)^2}+0.5\right]](_images/math/72af5b02650c05fb4f4eb6b609e0fc715d7f0fb9.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
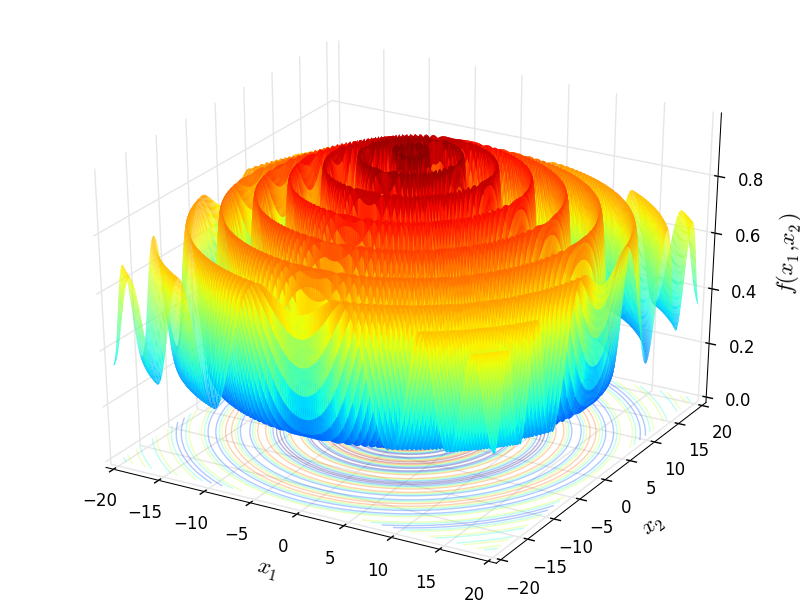
Two-dimensional SineEnvelope function
Global optimum:  for
for  for
for 
Six Hump Camel test objective function.
This class defines the Six Hump Camel global optimization problem. This is a multimodal minimization problem defined as follows:
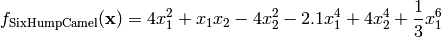
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
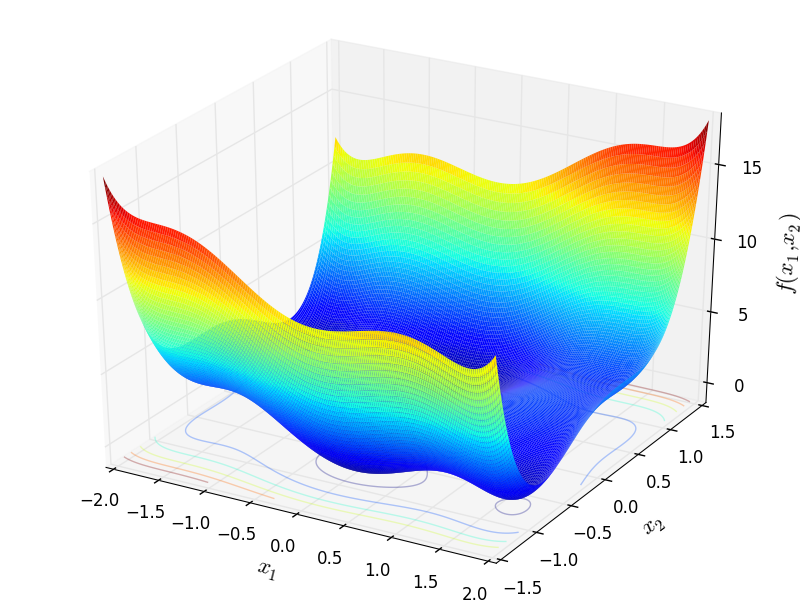
Two-dimensional Six Hump Camel function
Global optimum: 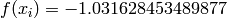 for
for ![\mathbf{x} = [0.08984201368301331 , -0.7126564032704135]](_images/math/67bd35625e41bbb7d0b6fd3d7442b2b33b122bf2.png) or
or ![\mathbf{x} = [-0.08984201368301331, 0.7126564032704135]](_images/math/bdf3285a889a30cd96ab47f6216ae5112a8787ca.png)
Sodp test objective function.
This class defines the Sum Of Different Powers global optimization problem. This is a multimodal minimization problem defined as follows:
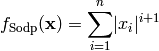
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
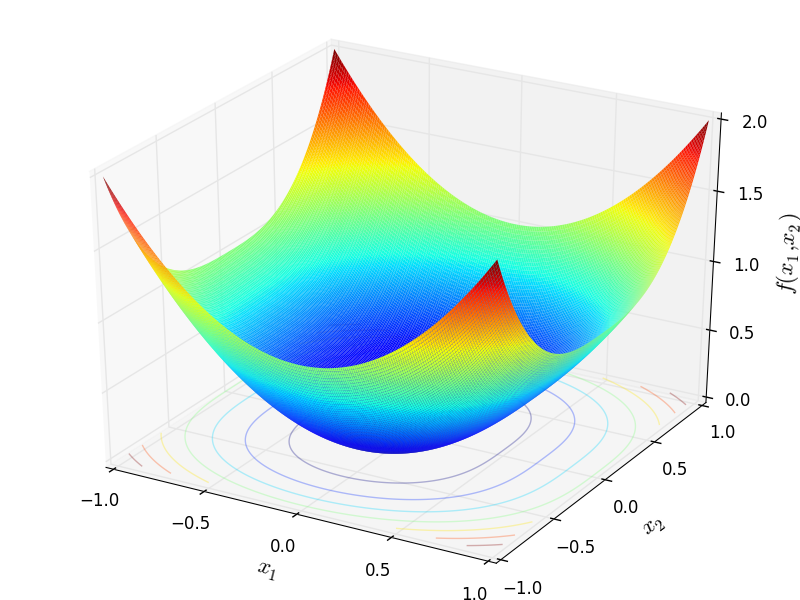
Two-dimensional Sum Of Different Powers function
Global optimum:  for
for  for
for 
Sphere test objective function.
This class defines the Sphere global optimization problem. This is a multimodal minimization problem defined as follows:
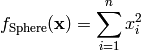
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
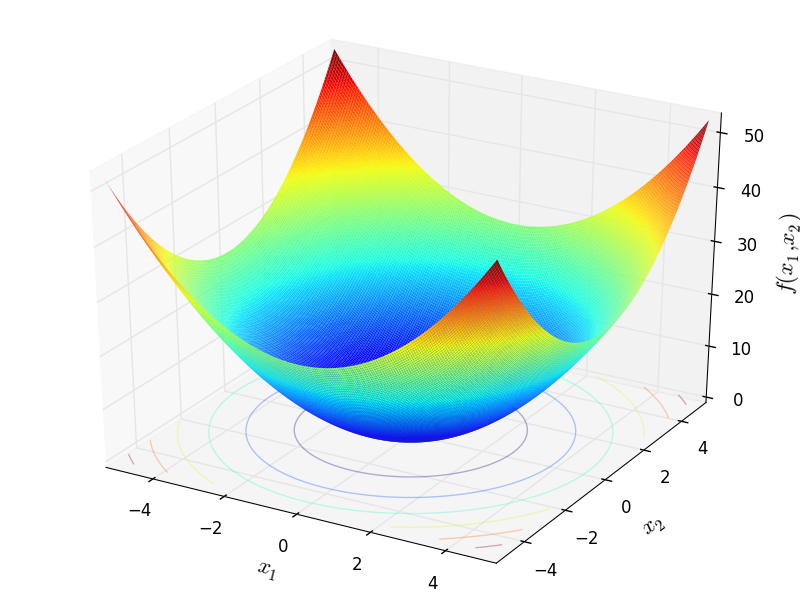
Two-dimensional Sphere function
Global optimum:  for
for  for
for 
Step test objective function.
This class defines the Step global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
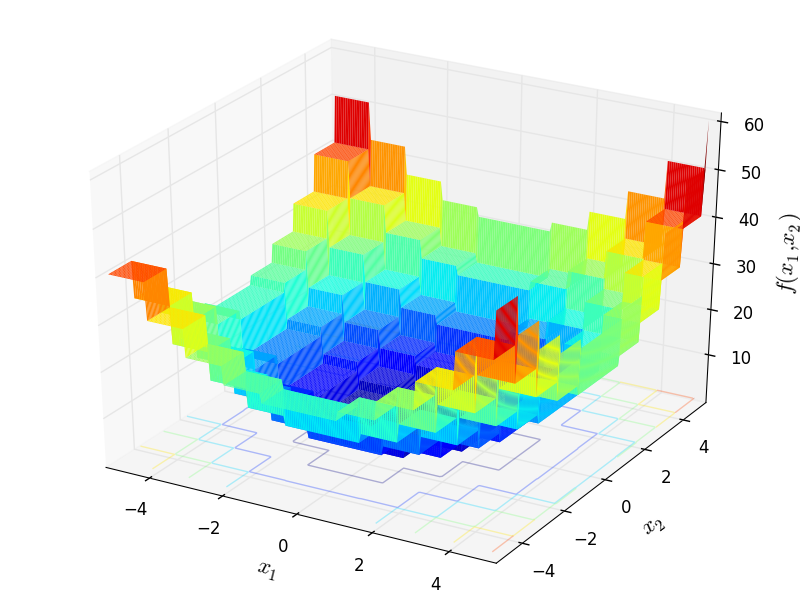
Two-dimensional Step function
Global optimum:  for
for 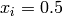 for
for 
Stochastic test objective function.
This class defines a Stochastic global optimization problem. This is a multimodal minimization problem defined as follows:
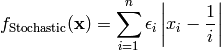
The variable 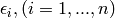 is a random variable uniformly distributed in
is a random variable uniformly distributed in ![[0, 1]](_images/math/ab178d831a786b92cb4c9ddc2d33578223036f98.png) .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
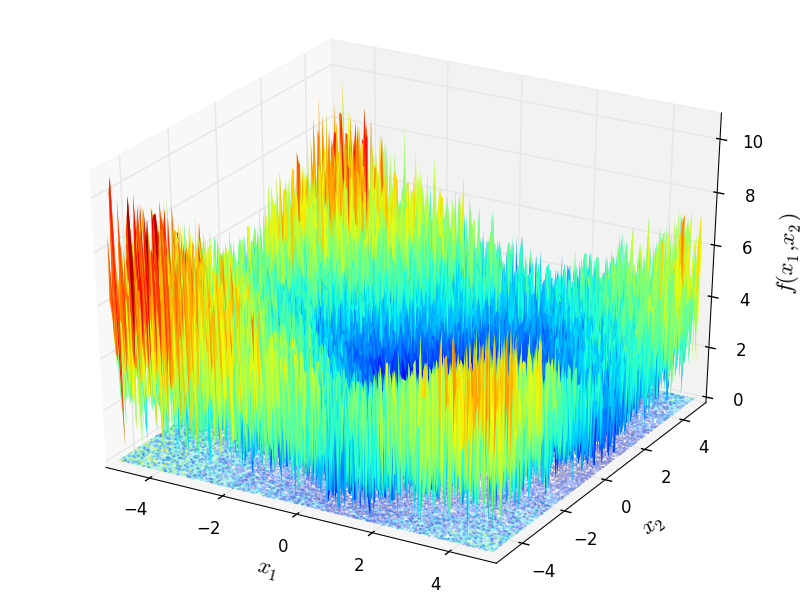
Two-dimensional Stochastic function
Global optimum:  for
for ![x_i = [1/n]](_images/math/076d6bda9c86979a469a0054ee62a82c3b20eefc.png) for
for 
StretchedV test objective function.
This class defines the Stretched V global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{StretchedV}}(\mathbf{x}) = \sum_{i=1}^{n-1} t^{1/4} [\sin (50t^{0.1}) + 1]^2](_images/math/653f0b6c39e2381ae62295cb1e9a86663efcca2e.png)
Where, in this exercise:
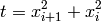
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
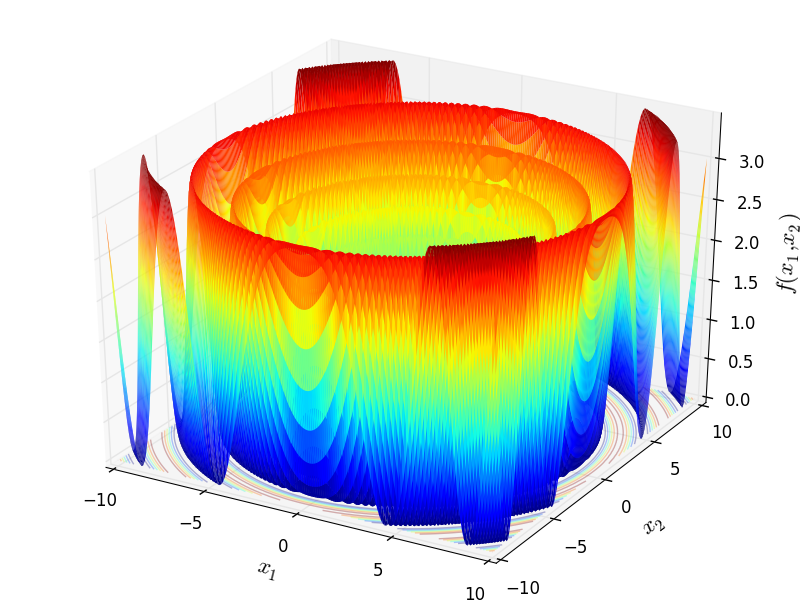
Two-dimensional StretchedV function
Global optimum:  for
for ![\mathbf{x} = [-9.38723188, 9.34026753]](_images/math/29eb1e580201d3aa9116a607cab42dad2d96479b.png) when
when 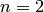 .
.
StyblinskiTang test objective function.
This class defines the Styblinski-Tang global optimization problem. This is a multimodal minimization problem defined as follows:
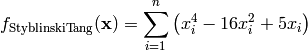
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
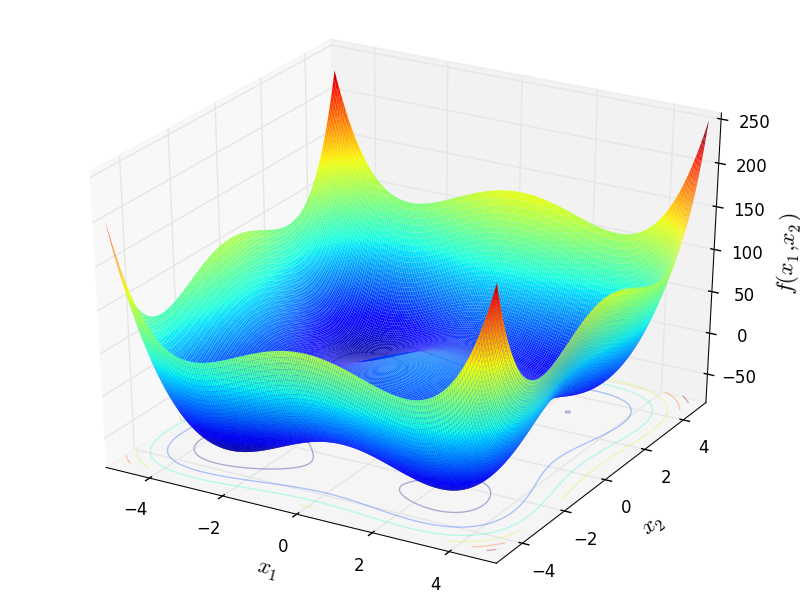
Two-dimensional Styblinski-Tang function
Global optimum:  for
for 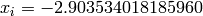 for
for 