 N-D Test Functions R¶
N-D Test Functions R¶Rana test objective function.
This class defines the Rana global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rana}}(\mathbf{x}) = \sum_{i=1}^{n} \left[x_{i} \sin\left(\sqrt{\lvert{x_{1} - x_{i} + 1}\rvert}\right) \cos\left(\sqrt{\lvert{x_{1} + x_{i} + 1}\rvert}\right) + \left(x_{1} + 1\right) \sin\left(\sqrt{\lvert{x_{1} + x_{i} + 1}\rvert}\right) \cos\left(\sqrt{\lvert{x_{1} - x_{i} + 1}\rvert}\right)\right]](_images/math/661e35f80e88293d3f8f028f11d03da3f6c4bfc7.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500.000001, 500.000001]](_images/math/7df4f011022beda362419d4572afd5d400600330.png) for
for  .
.
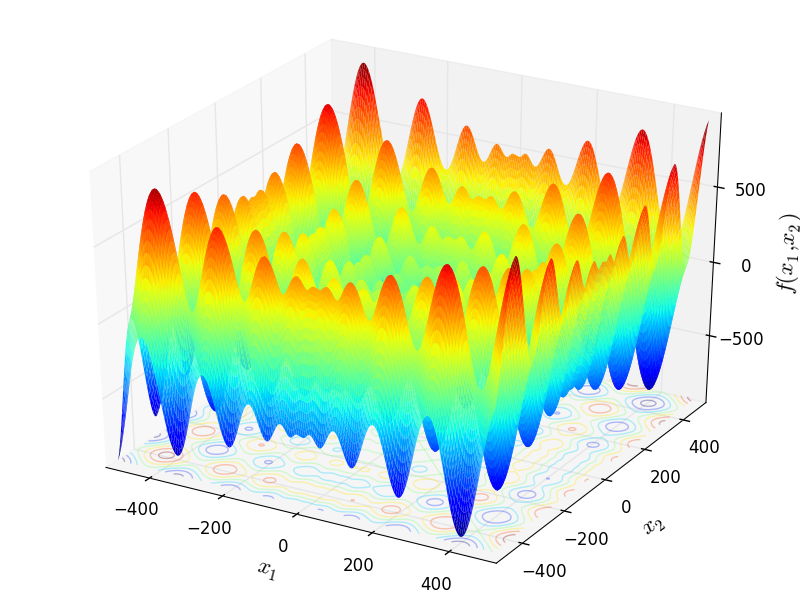
Two-dimensional Rana function
Global optimum: 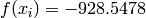 for
for  for
for 
Rastrigin test objective function.
This class defines the Rastrigin global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rastrigin}}(\mathbf{x}) = 10n \sum_{i=1}^n \left[ x_i^2 - 10 \cos(2\pi x_i) \right]](_images/math/cd42e559a10cceea8a537e17e665ca0dfbafdf88.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.
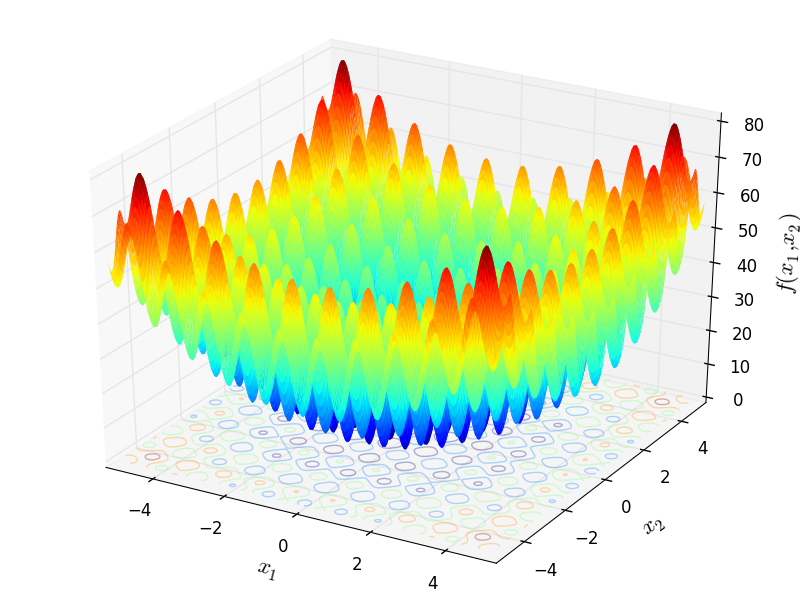
Two-dimensional Rastrigin function
Global optimum:  for
for 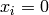 for
for 
Ripple 1 test objective function.
This class defines the Ripple 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Ripple01}}(\mathbf{x}) = \sum_{i=1}^2 -e^{-2 \log 2 (\frac{x_i-0.1}{0.8})^2} \left[\sin^6(5 \pi x_i) + 0.1\cos^2(500 \pi x_i) \right]](_images/math/dff40753ebc58367b28e3cf7a10cc0ec01d7159b.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
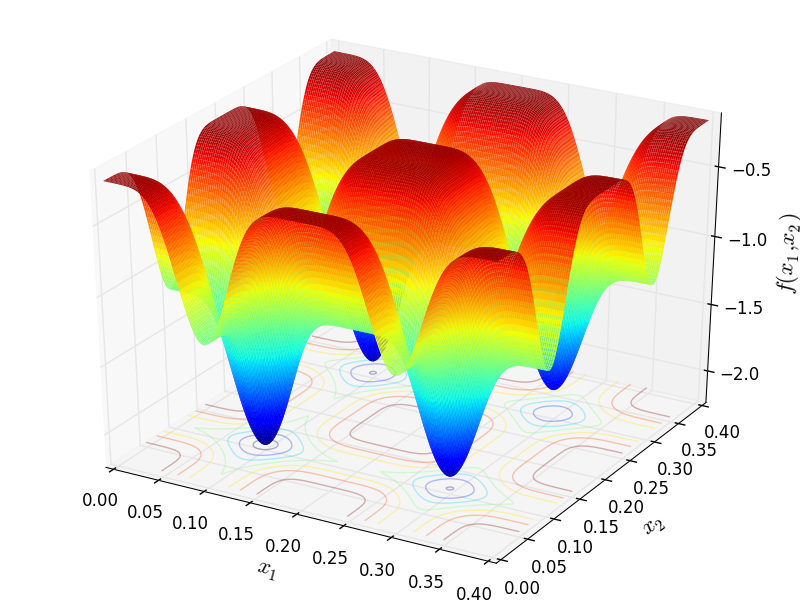
Two-dimensional Ripple 1 function
Global optimum: 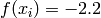 for
for 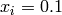 for
for 
Ripple 25 test objective function.
This class defines the Ripple 25 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Ripple25}}(\mathbf{x}) = \sum_{i=1}^2 -e^{-2 \log 2 (\frac{x_i-0.1}{0.8})^2} \left[\sin^6(5 \pi x_i) \right]](_images/math/6fecb38af74a7283a5521c999daa70b174c31b32.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
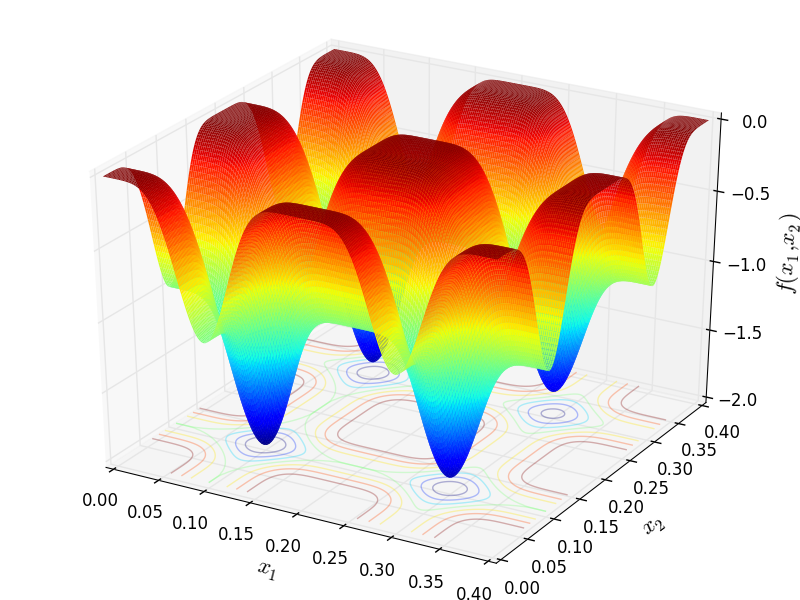
Two-dimensional Ripple 25 function
Global optimum: 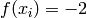 for
for 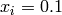 for
for 
Rosenbrock test objective function.
This class defines the Rosenbrock global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Rosenbrock}}(\mathbf{x}) = \sum_{i=1}^{n-1} [100(x_i^2 - x_{i+1})^2 + (x_i - 1)^2]](_images/math/7f3dc2e29c0b7a1cf4488ee8ec82be110658a58b.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 10]](_images/math/98df04fbd9b8266181439af788bf1880288e02c8.png) for
for  .
.
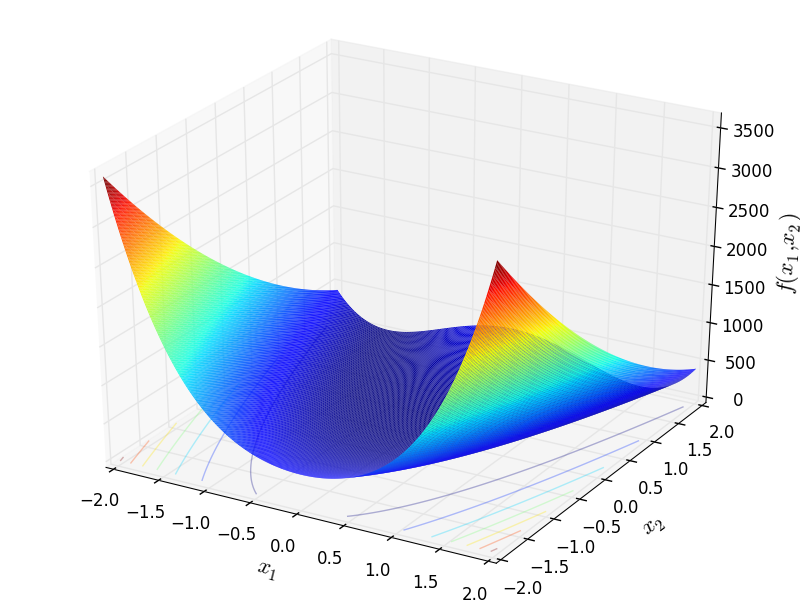
Two-dimensional Rosenbrock function
Global optimum:  for
for 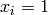 for
for 
Modified Rosenbrock test objective function.
This class defines the Modified Rosenbrock global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-2, 2]](_images/math/3220cc226a0abf06f00e70257db97b5c754120f7.png) for
for  .
.
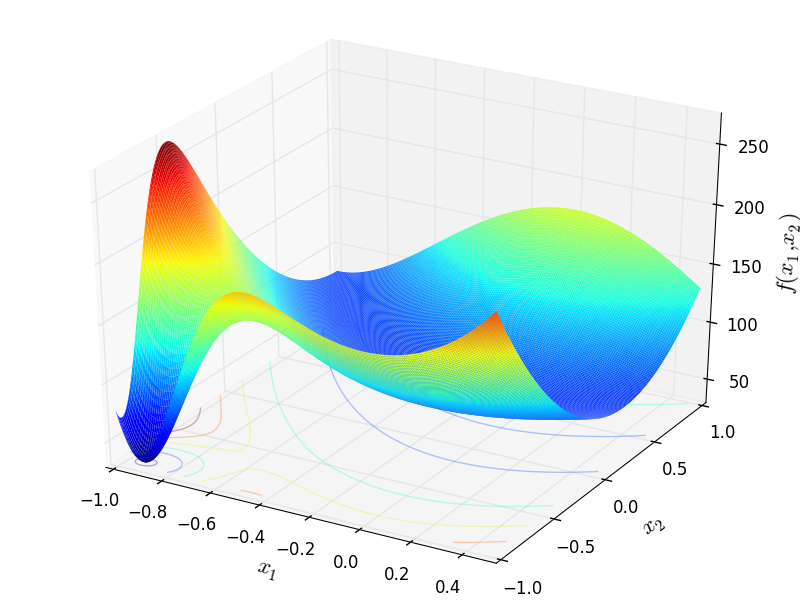
Two-dimensional Modified Rosenbrock function
Global optimum:  for
for ![\mathbf{x} = [-0.9, -0.95]](_images/math/0e3c2b391b53f2ffd7150bde7c1766da7a65aaf3.png)
Rotated Ellipse 1 test objective function.
This class defines the Rotated Ellipse 1 global optimization problem. This is a unimodal minimization problem defined as follows:
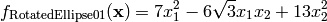
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
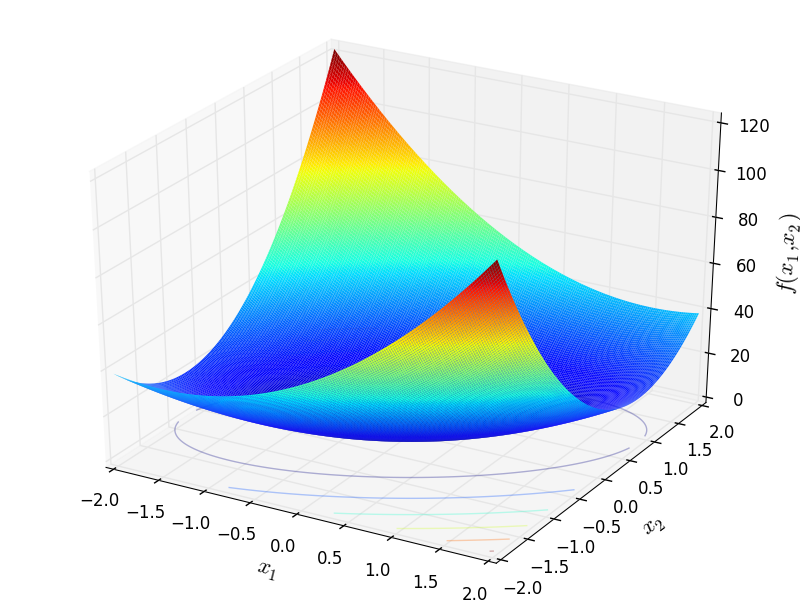
Two-dimensional Rotated Ellipse 1 function
Global optimum:  for
for ![\mathbf{x} = [0, 0]](_images/math/ae446016118c18b04012af8feda9cc5e2e1808a6.png)
Rotated Ellipse 2 test objective function.
This class defines the Rotated Ellipse 2 global optimization problem. This is a unimodal minimization problem defined as follows:
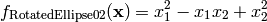
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
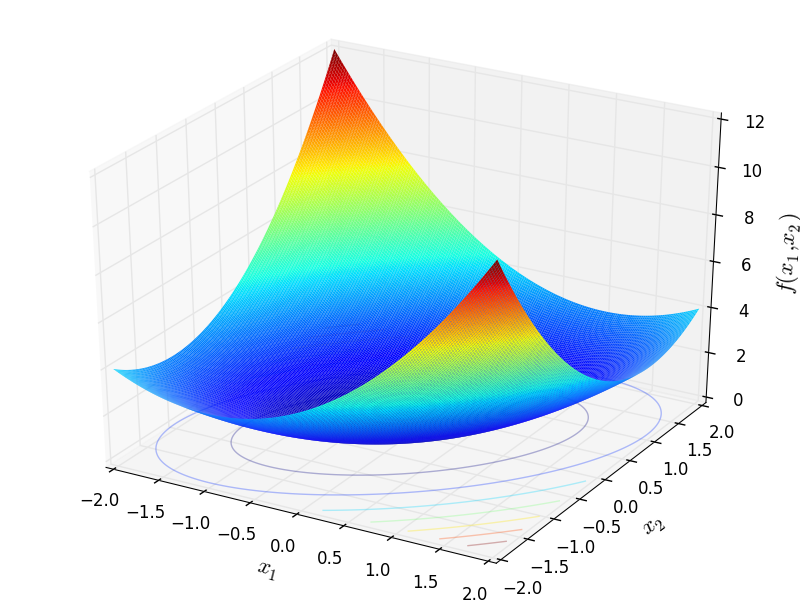
Two-dimensional Rotated Ellipse 2 function
Global optimum:  for
for ![\mathbf{x} = [0, 0]](_images/math/ae446016118c18b04012af8feda9cc5e2e1808a6.png)