 N-D Test Functions Q¶
N-D Test Functions Q¶Qing test objective function.
This class defines the Qing global optimization problem. This is a multimodal minimization problem defined as follows:
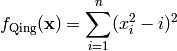
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
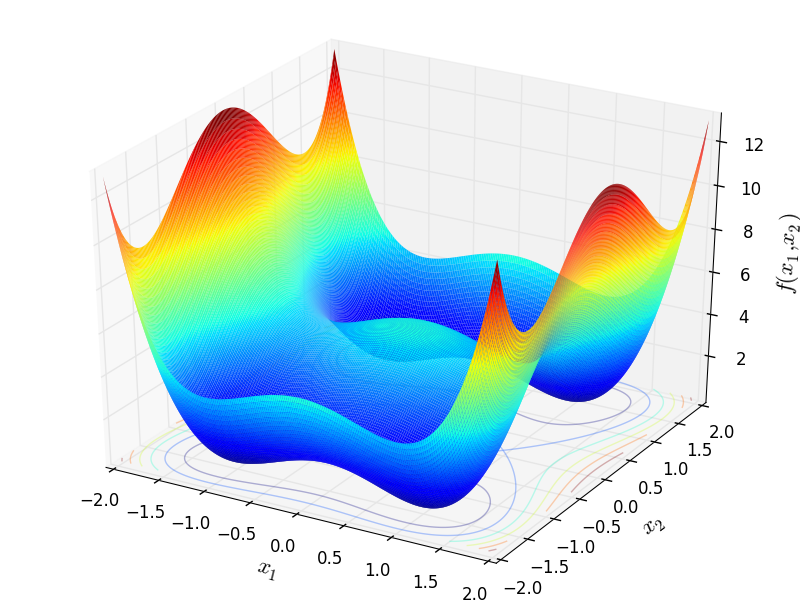
Two-dimensional Qing function
Global optimum:  for
for 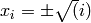 for
for 
Quadratic test objective function.
This class defines the Quadratic global optimization problem. This is a multimodal minimization problem defined as follows:
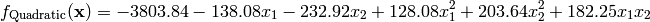
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
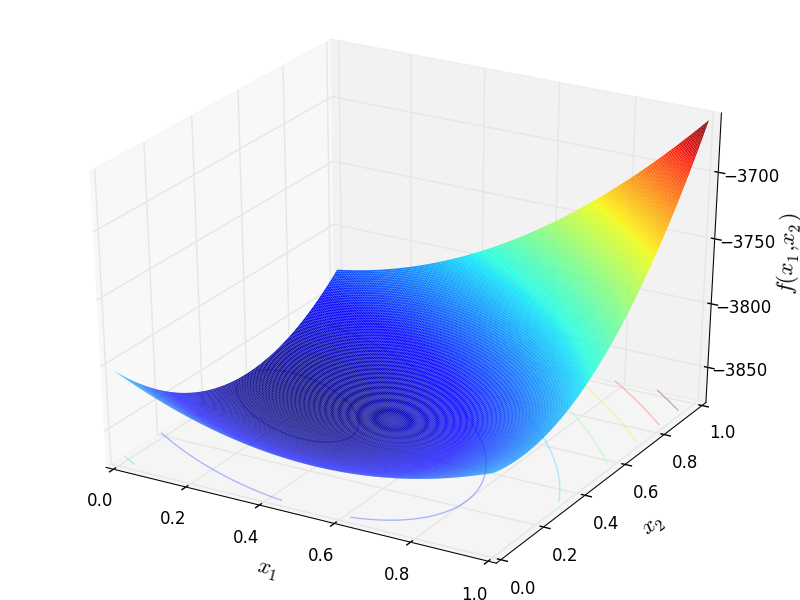
Two-dimensional Quadratic function
Global optimum:  for
for ![\mathbf{x} = [0.19388, 0.48513]](_images/math/9bfc34d01e61936a1cf0d0b35fbba5ad34ffc75c.png)
Quintic test objective function.
This class defines the Quintic global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
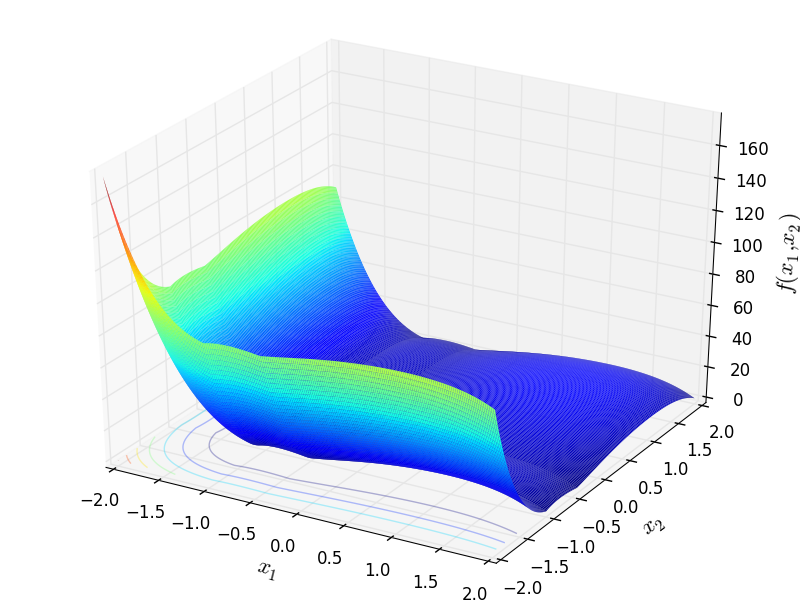
Two-dimensional Quintic function
Global optimum:  for
for 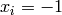 for
for 