 N-D Test Functions P¶
N-D Test Functions P¶Parsopoulos test objective function.
This class defines the Parsopoulos global optimization problem. This is a multimodal minimization problem defined as follows:
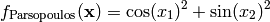
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.

Two-dimensional Parsopoulos function
Global optimum: This function has infinite number of global minima in R2, at points  ,
where
,
where 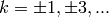 and
and 
In the given domain problem, function has 12 global minima all equal to zero.
Pathological test objective function.
This class defines the Pathological global optimization problem. This is a multimodal minimization problem defined as follows:
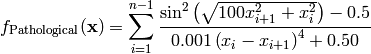
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
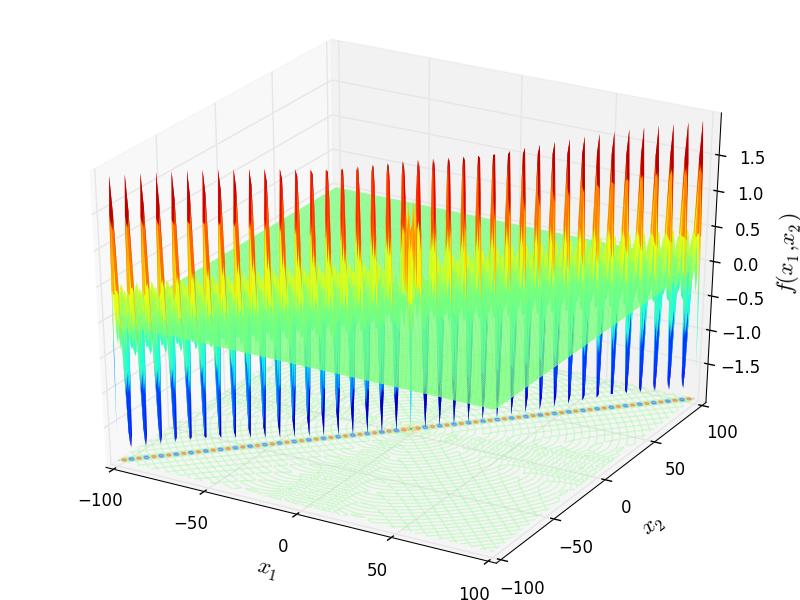
Two-dimensional Pathological function
Global optimum: 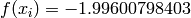 for
for  for
for 
Paviani test objective function.
This class defines the Paviani global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Paviani}}(\mathbf{x}) = \sum_{i=1}^{10} \left[\log^{2}\left(10 - x_i\right) + \log^{2}\left(x_i -2\right)\right] - \left(\prod_{i=1}^{10} x_i^{10} \right)^{0.2}](_images/math/e9004b1ed31a772bbb76eb6168f17ab8f46ef6af.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [2.001, 9.999]](_images/math/636468723f60098daa93400984ff0cd953b9408c.png) for
for  .
.
Global optimum:  for
for 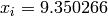 for
for 
Penalty 1 test objective function.
This class defines the Penalty 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Penalty01}}(\mathbf{x}) = \frac{\pi}{30} \left\{10 \sin^2(\pi y_1) + \sum_{i=1}^{n-1} (y_i - 1)^2 \left[1 + 10 \sin^2(\pi y_{i+1}) \right ] + (y_n - 1)^2 \right \} + \sum_{i=1}^n u(x_i, 10, 100, 4)](_images/math/8f84d6bf1a7c879c73145193287f25d29159af83.png)
Where, in this exercise:
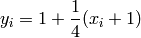
And:
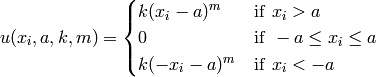
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
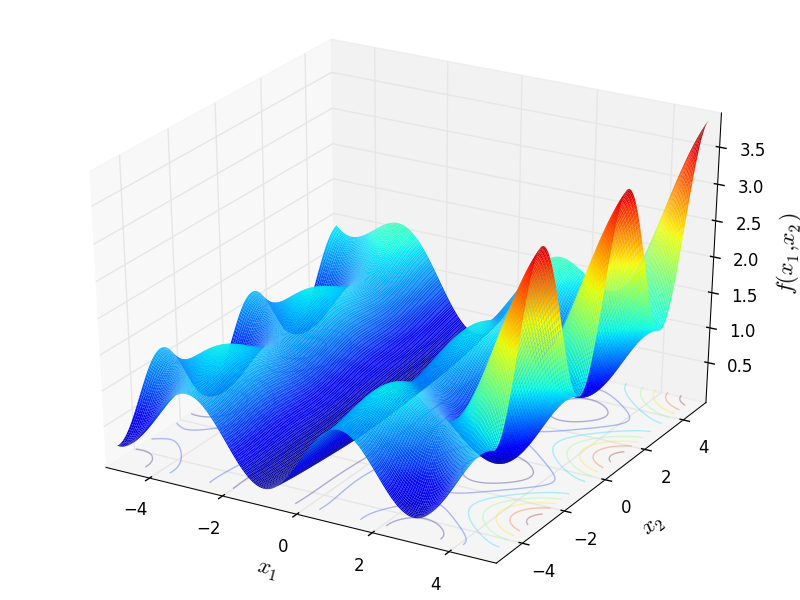
Two-dimensional Penalty 1 function
Global optimum:  for
for 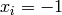 for
for 
Penalty 2 test objective function.
This class defines the Penalty 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Penalty02}}(\mathbf{x}) = 0.1 \left\{\sin^2(3\pi x_1) + \sum_{i=1}^{n-1} (x_i - 1)^2 \left[1 + \sin^2(3\pi x_{i+1}) \right ] + (x_n - 1)^2 \left [1 + \sin^2(2 \pi x_n) \right ]\right \} + \sum_{i=1}^n u(x_i, 5, 100, 4)](_images/math/e2fd35c148a58b75bd0725f24ce8ea75772f8f1f.png)
Where, in this exercise:
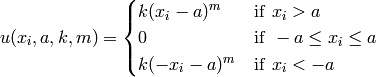
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
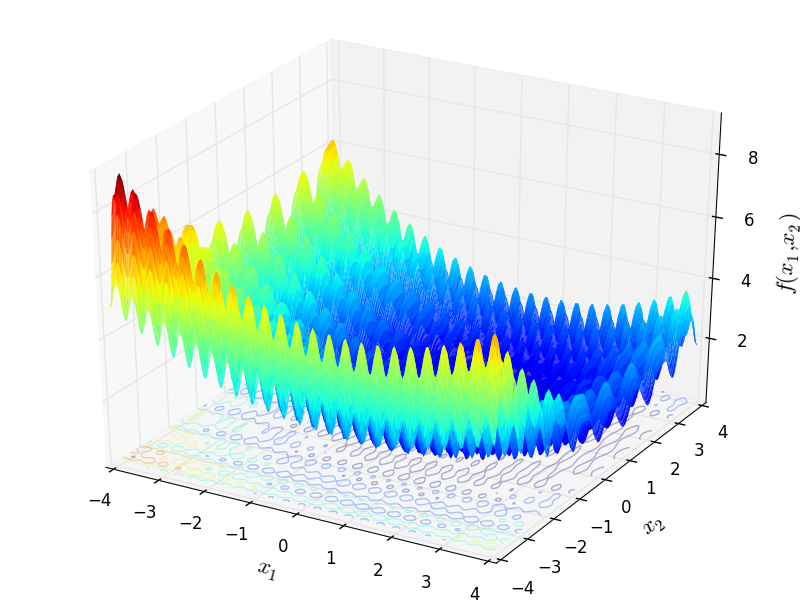
Two-dimensional Penalty 2 function
Global optimum:  for
for 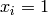 for
for 
PenHolder test objective function.
This class defines the PenHolder global optimization problem. This is a multimodal minimization problem defined as follows:
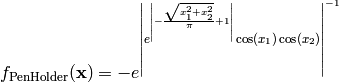
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-11, 11]](_images/math/64a0f2c8fc7fe30ca047d2d61f93c549fc261011.png) for
for  .
.
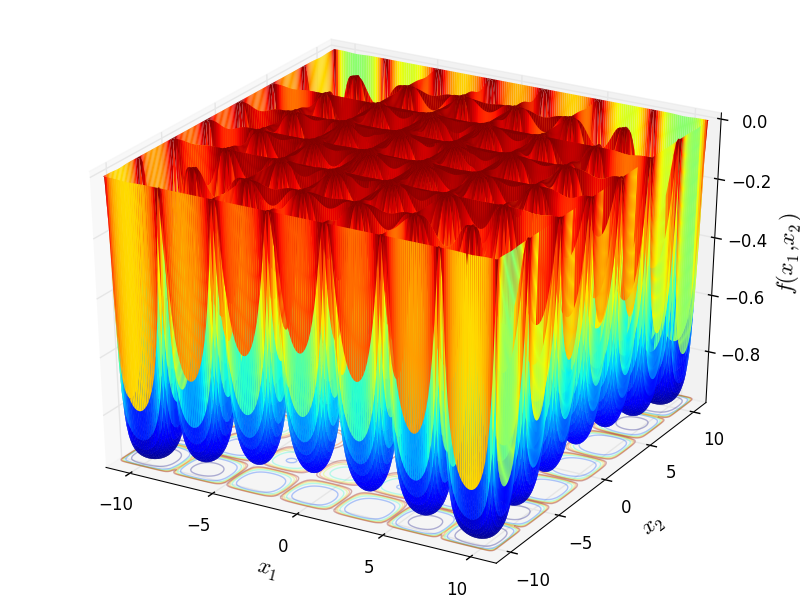
Two-dimensional PenHolder function
Global optimum: 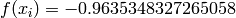 for
for  for
for 
PermFunction 1 test objective function.
This class defines the Perm Function 1 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PermFunction01}}(\mathbf{x}) = \sum_{k=1}^n \left\{ \sum_{j=1}^n (j^k + \beta) \left[ \left(\frac{x_j}{j}\right)^k - 1 \right] \right\}^2](_images/math/86131159d3a5713942ef9fa746f9e644c00ba1dd.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-n, n+1]](_images/math/e90363f6e33a222e1f7df54a9864b6465e704e3e.png) for
for  .
.
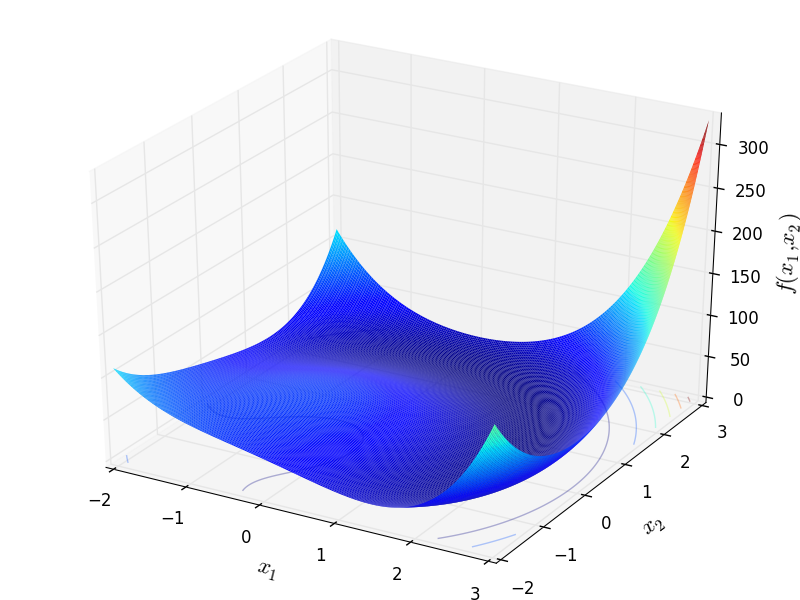
Two-dimensional PermFunction 1 function
Global optimum:  for
for  for
for 
PermFunction 2 test objective function.
This class defines the Perm Function 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PermFunction02}}(\mathbf{x}) = \sum_{k=1}^n \left\{ \sum_{j=1}^n (j + \beta) \left[ \left(x_j^k - \frac{1}{j} \right ) \right] \right\}^2](_images/math/2d6413650ad49e513fd577f73a3245f5964c44e5.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-n, n+1]](_images/math/e90363f6e33a222e1f7df54a9864b6465e704e3e.png) for
for  .
.
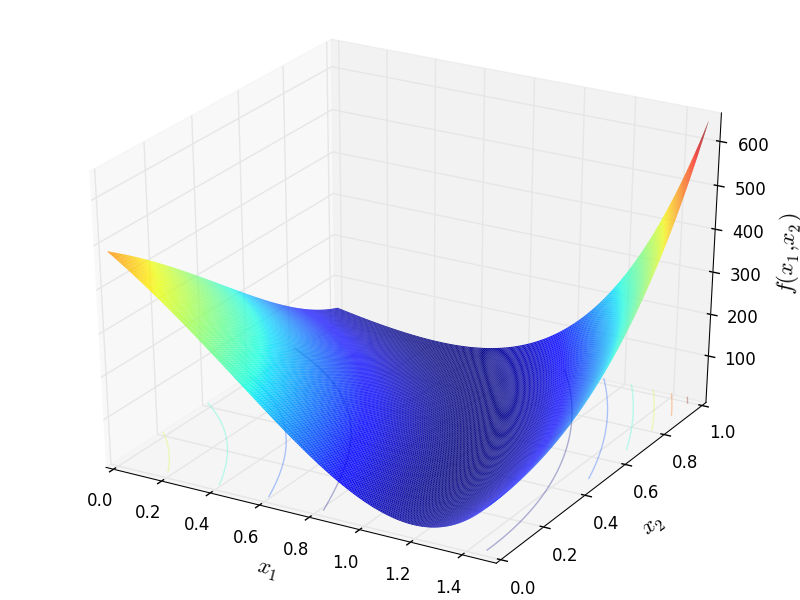
Two-dimensional PermFunction 2 function
Global optimum:  for
for 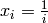 for
for 
Pinter test objective function.
This class defines the Pinter global optimization problem. This is a multimodal minimization problem defined as follows:
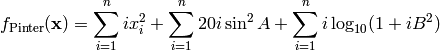
Where, in this exercise:
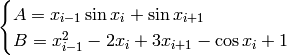
Where 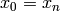 and
and 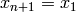 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
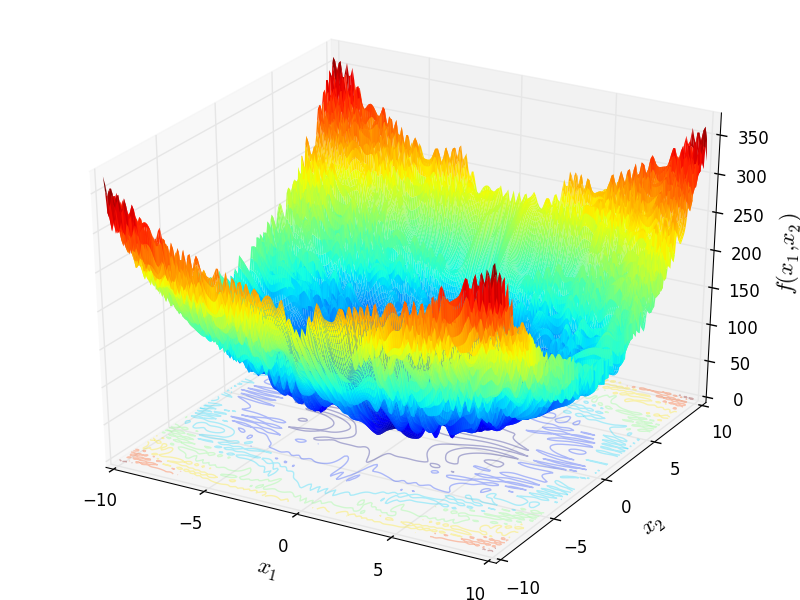
Two-dimensional Pinter function
Global optimum:  for
for  for
for 
Plateau test objective function.
This class defines the Plateau global optimization problem. This is a multimodal minimization problem defined as follows:
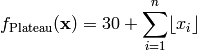
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.
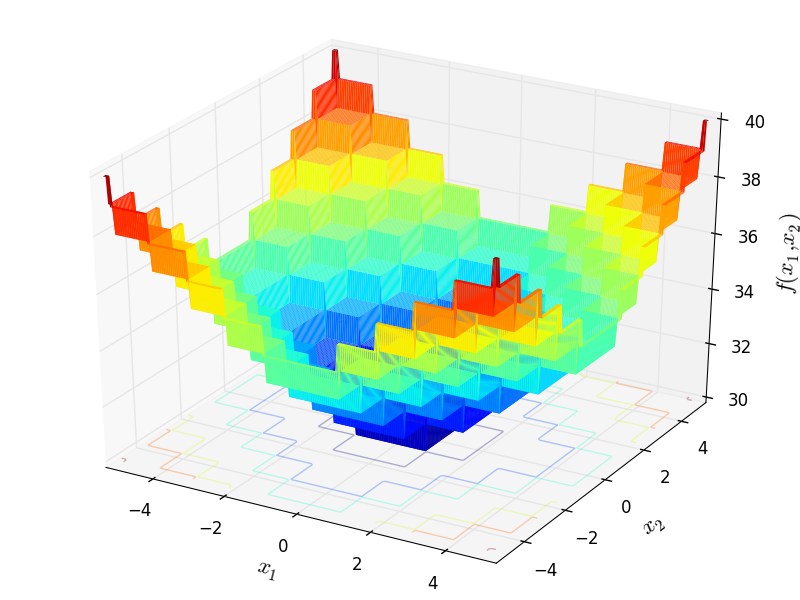
Two-dimensional Plateau function
Global optimum:  for
for  for
for 
Powell test objective function.
This class defines the Powell global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-4, 5]](_images/math/a8851241896afaa6b5f64eff8d113a185f56a5ed.png) for
for  .
.
Global optimum:  for
for  for
for 
Power sum test objective function.
This class defines the Power Sum global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{PowerSum}}(\mathbf{x}) = \sum_{k=1}^n\left[\left(\sum_{i=1}^n x_i^k \right) - b_k \right]^2](_images/math/9021e8055786a6b5e161b7d05ed33d707ca68bd4.png)
Where, in this exercise, ![\mathbf{b} = [8, 18, 44, 114]](_images/math/60aa4fd2d6f185448a71c22abdde0bce511e1128.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 4]](_images/math/e85f9417023b4ca79e827af77dce3a90c436cad5.png) for
for  .
.
Global optimum:  for
for ![\mathbf{x} = [1, 2, 2, 3]](_images/math/2a08212ee3af188ac51fd229b1d4454e31240664.png)
Price 1 test objective function.
This class defines the Price 1 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-500, 500]](_images/math/286a33626f115cb9d7e75a098b287cf93b7916e5.png) for
for  .
.
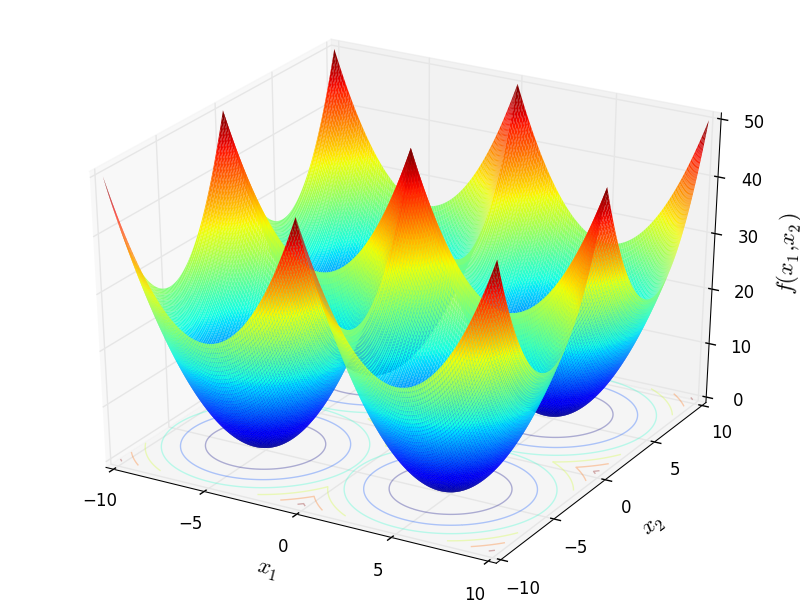
Two-dimensional Price 1 function
Global optimum:  for
for ![\mathbf{x} = [5, 5]](_images/math/418e74c9c24b213c723e292c30dbf8df56578d19.png) or
or ![\mathbf{x} = [5, -5]](_images/math/649c0673ea0c64fdb099e46030c8c3948cf25c13.png) or
or ![\mathbf{x} = [-5, 5]](_images/math/9ac5f7de3a7a0bc077c698d871ab71f70ecdf449.png) or
or ![\mathbf{x} = [-5, -5]](_images/math/c919182eb588895f12fa465da74a349e5f99f8b1.png)
Price 2 test objective function.
This class defines the Price 2 global optimization problem. This is a multimodal minimization problem defined as follows:
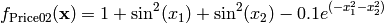
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
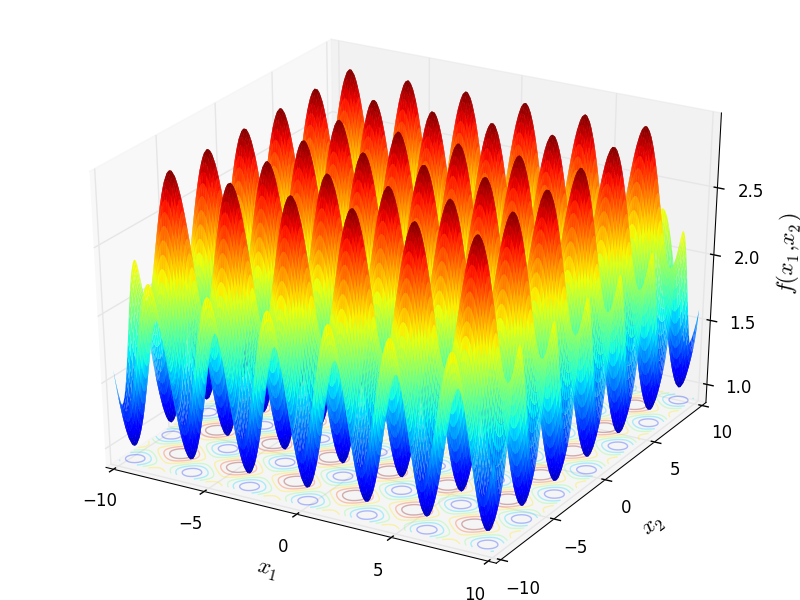
Two-dimensional Price 2 function
Global optimum:  for
for  for
for 
Price 3 test objective function.
This class defines the Price 3 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Price03}}(\mathbf{x}) = 100(x_2 - x_1^2)^2 + \left[6.4(x_2 - 0.5)^2 - x_1 - 0.6 \right]^2](_images/math/ed1c7bd06827610a030b02fcddadfb13ff9b31da.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
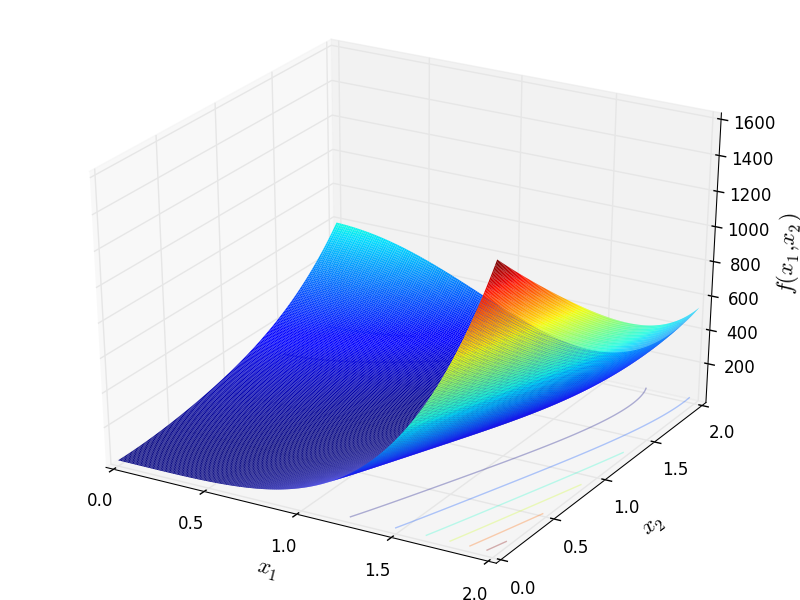
Two-dimensional Price 3 function
Global optimum:  for
for ![\mathbf{x} = [-5, -5]](_images/math/c919182eb588895f12fa465da74a349e5f99f8b1.png) ,
, ![\mathbf{x} = [-5, 5]](_images/math/9ac5f7de3a7a0bc077c698d871ab71f70ecdf449.png) ,
,
![\mathbf{x} = [5, -5]](_images/math/649c0673ea0c64fdb099e46030c8c3948cf25c13.png) ,
, ![\mathbf{x} = [5, 5]](_images/math/418e74c9c24b213c723e292c30dbf8df56578d19.png)
Price 4 test objective function.
This class defines the Price 4 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-50, 50]](_images/math/9479281c91e8220b33050faa5474b724a60cf1ea.png) for
for  .
.
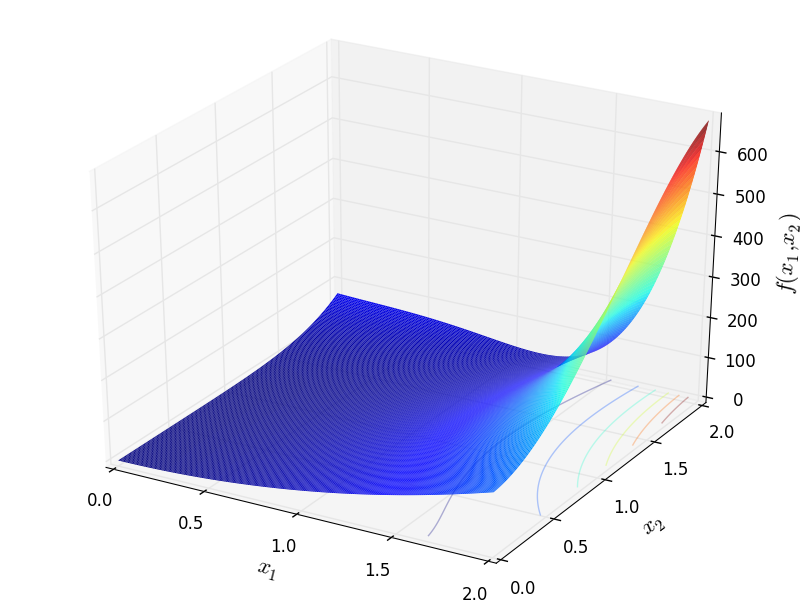
Two-dimensional Price 4 function
Global optimum:  for
for ![\mathbf{x} = [0, 0]](_images/math/ae446016118c18b04012af8feda9cc5e2e1808a6.png) ,
, ![\mathbf{x} = [2, 4]](_images/math/cfebedfefc02ae410982d1be30f4a9063b7de936.png) and
and
![\mathbf{x} = [1.464, -2.506]](_images/math/0481e55c9268e119e9d1f1452a36fa9f90e9713e.png)