 N-D Test Functions U¶
N-D Test Functions U¶Ursem 1 test objective function.
This class defines the Ursem 1 global optimization problem. This is a unimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_1 \in [-2.5, 3]](_images/math/69603cd07bd82a424c482930373352d2f9f8b9d3.png) ,
, ![x_2 \in [-2, 2]](_images/math/9217e1eab45a4763bba67af221a49dd040b53d7b.png) .
.
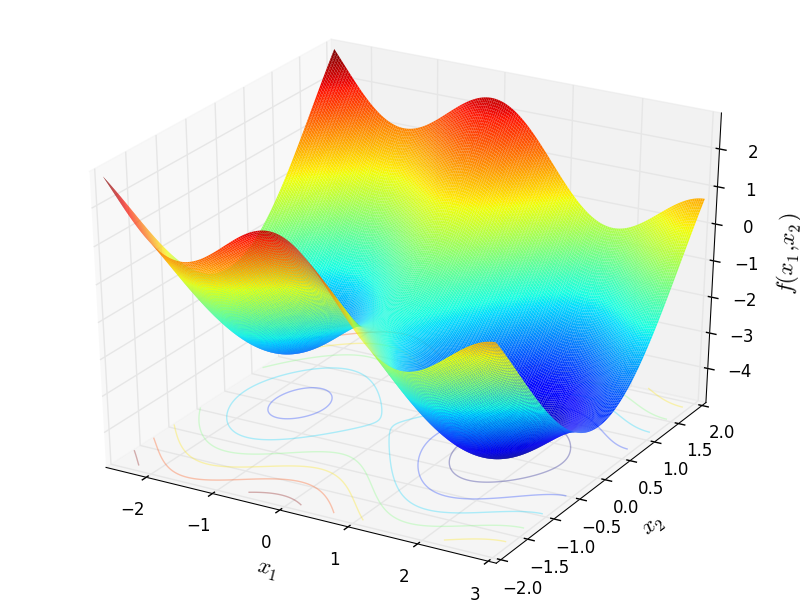
Two-dimensional Ursem 1 function
Global optimum:  for
for ![\mathbf{x} = [1.69714, 0.0]](_images/math/bebab4683be9d26ce3b1d3f505bd8214ce19ab4c.png)
Ursem 3 test objective function.
This class defines the Ursem 3 global optimization problem. This is a multimodal minimization problem defined as follows:
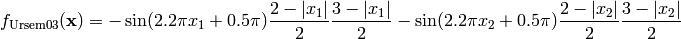
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_1 \in [-2, 2]](_images/math/b8015ed2833b045f624a5d328834954a1654fa1f.png) ,
, ![x_2 \in [-1.5, 1.5]](_images/math/4fbb6c96a8e6f78a4276b1d597d9777d441c380d.png) .
.
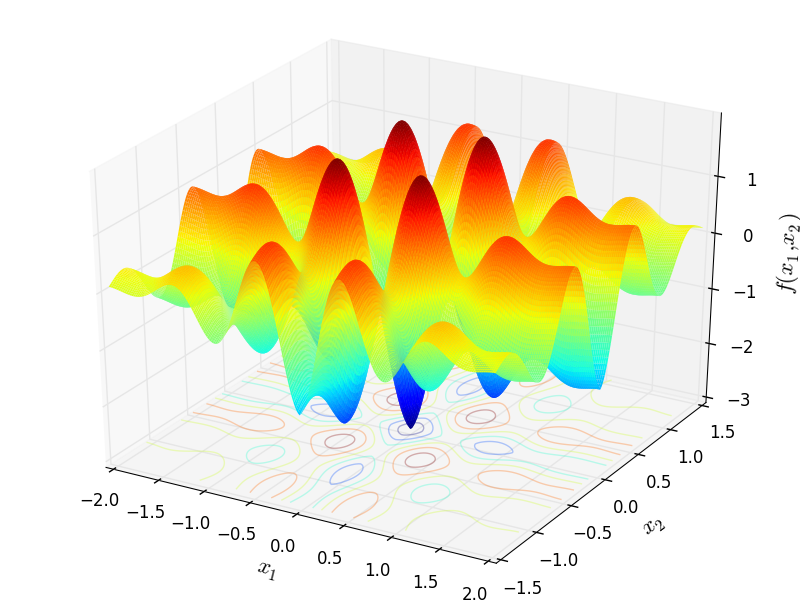
Two-dimensional Ursem 3 function
Global optimum: 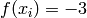 for
for 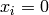 for
for 
Ursem 4 test objective function.
This class defines the Ursem 4 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-2, 2]](_images/math/3220cc226a0abf06f00e70257db97b5c754120f7.png) for
for  .
.
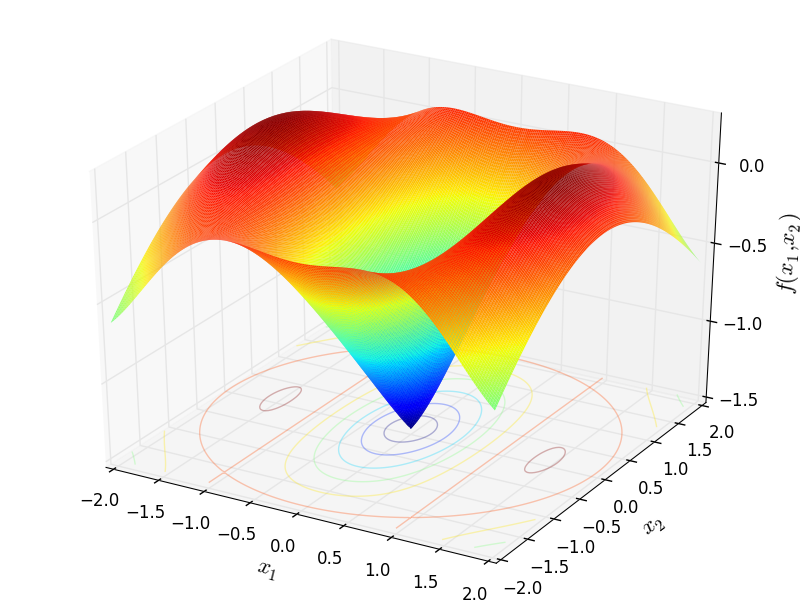
Two-dimensional Ursem 4 function
Global optimum: 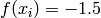 for
for 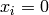 for
for 
Ursem Waves test objective function.
This class defines the Ursem Waves global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{UrsemWaves}}(\mathbf{x}) = -0.9x_1^2 + (x_2^2 - 4.5x_2^2)x_1x_2 + 4.7 \cos \left[ 2x_1 - x_2^2(2 + x_1) \right ] \sin(2.5 \pi x_1)](_images/math/18e950b5e64b56ac04ed4c2b6a0165a93daa143f.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_1 \in [-0.9, 1.2]](_images/math/967f44a5282ef8f67b47dc9043d2620efecc0297.png) ,
, ![x_2 \in [-1.2, 1.2]](_images/math/a3942a3d02a52ef92edc194d8dc6ae3fe5f6f24d.png) .
.
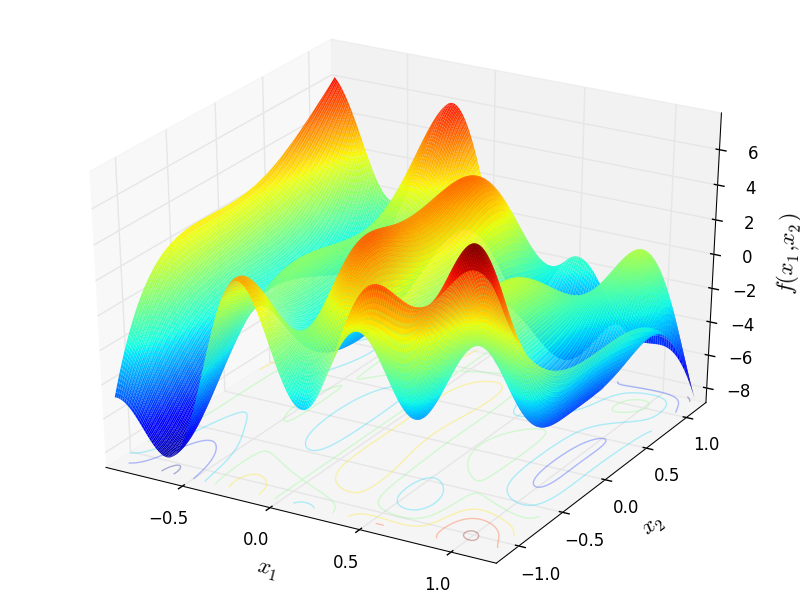
Two-dimensional Ursem Waves function
Global optimum: 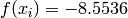 for
for 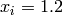 for
for 