 N-D Test Functions M¶
N-D Test Functions M¶Matyas test objective function.
This class defines the Matyas global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
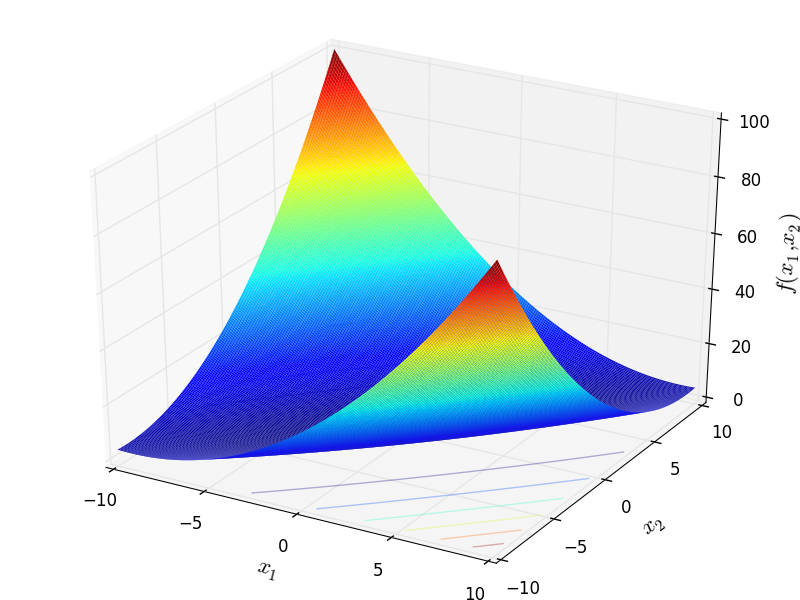
Two-dimensional Matyas function
Global optimum:  for
for 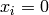 for
for 
McCormick test objective function.
This class defines the McCormick global optimization problem. This is a multimodal minimization problem defined as follows:
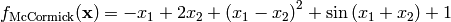
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_1 \in [-1.5, 4]](_images/math/c222decd8b0efcfd109bde524102428dfc8ea55f.png) ,
, ![x_2 \in [-3, 4]](_images/math/a08c2638cc73d2c0c76fcebaf08d0531766bee9c.png) .
.
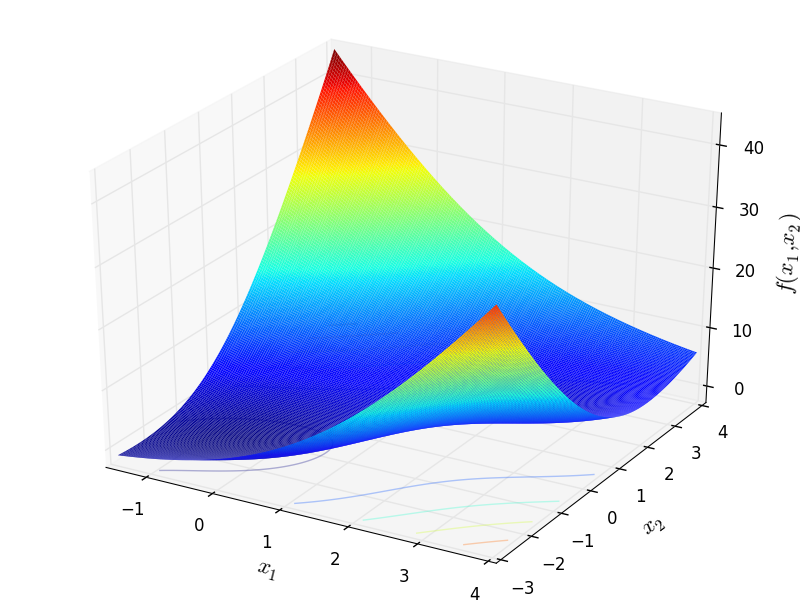
Two-dimensional McCormick function
Global optimum: 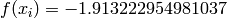 for
for ![\mathbf{x} = [-0.5471975602214493, -1.547197559268372]](_images/math/7589ac6c12fcf8402683d2aedc57a631bbf48b20.png)
Michalewicz test objective function.
This class defines the Michalewicz global optimization problem. This is a multimodal minimization problem defined as follows:

Where, in this exercise, 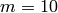 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, \pi]](_images/math/10b9f829ecf73e20ecc5c80159a1d1615d4c0f6a.png) for
for  .
.
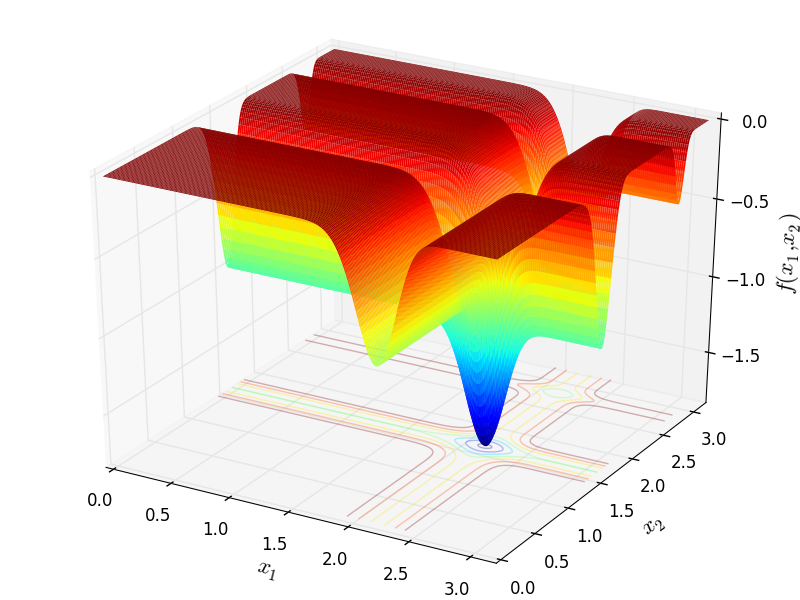
Two-dimensional Michalewicz function
Global optimum: 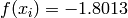 for
for 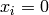 for
for 
Miele-Cantrell test objective function.
This class defines the Miele-Cantrell global optimization problem. This is a multimodal minimization problem defined as follows:
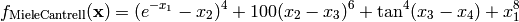
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
Global optimum:  for
for ![\mathbf{x} = [0, 1, 1, 1]](_images/math/cf25b6256b504a94eee8ba1895a66358db1fce20.png)
Mishra 1 test objective function.
This class defines the Mishra 1 global optimization problem. This is a multimodal minimization problem defined as follows:
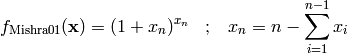
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
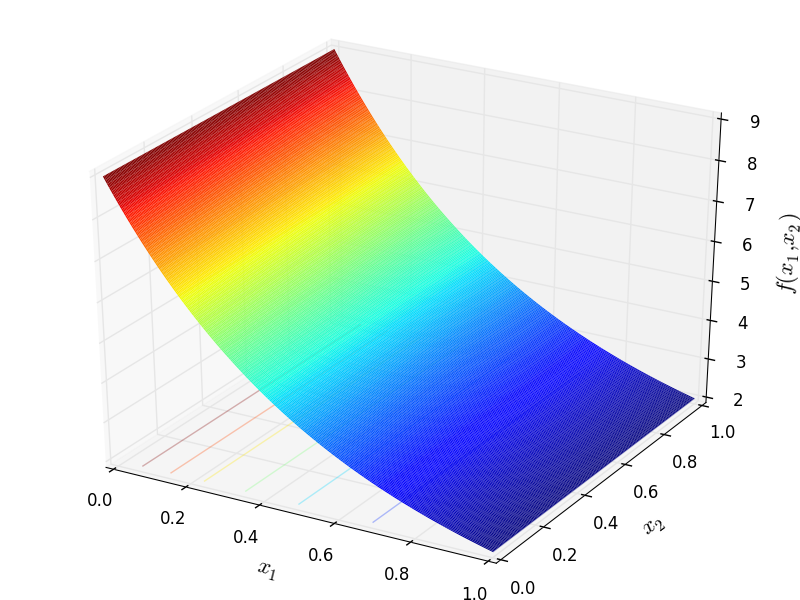
Two-dimensional Mishra 1 function
Global optimum: 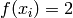 for
for 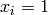 for
for 
Mishra 2 test objective function.
This class defines the Mishra 2 global optimization problem. This is a multimodal minimization problem defined as follows:
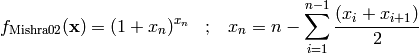
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
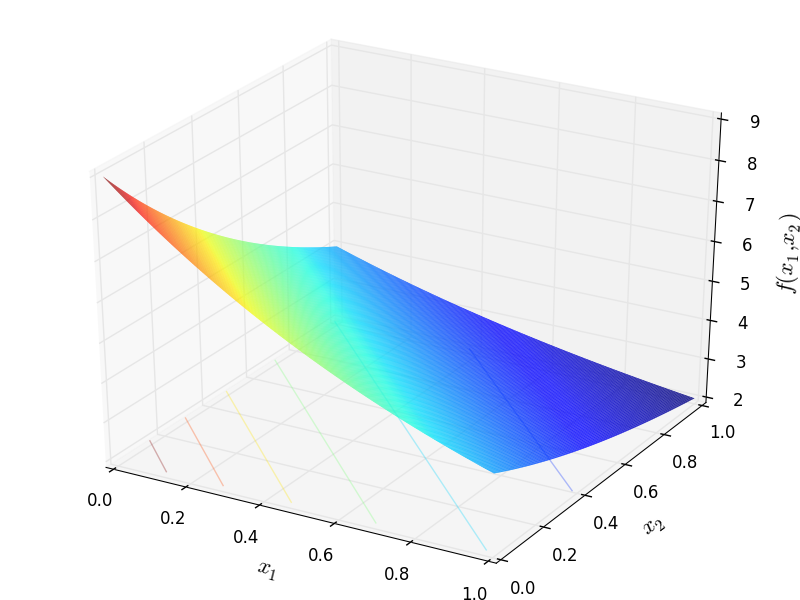
Two-dimensional Mishra 2 function
Global optimum: 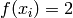 for
for 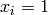 for
for 
Mishra 3 test objective function.
This class defines the Mishra 3 global optimization problem. This is a multimodal minimization problem defined as follows:
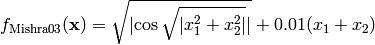
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
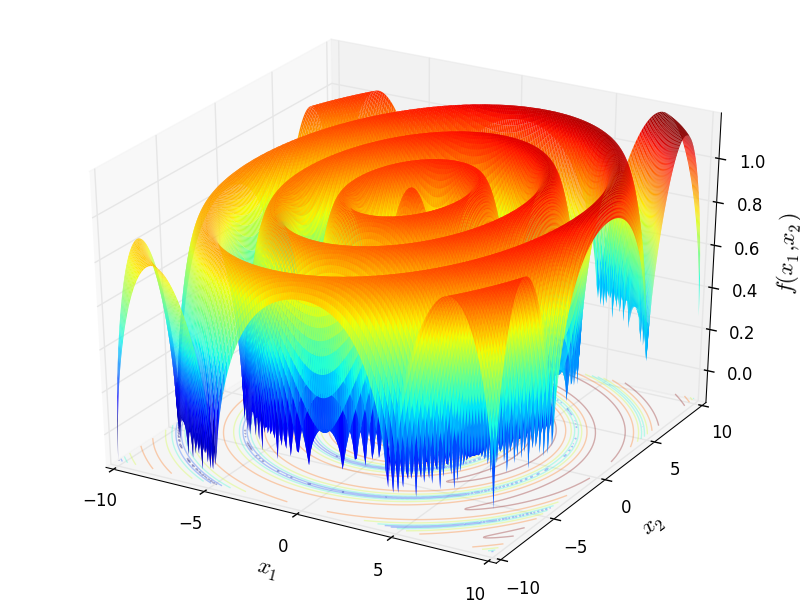
Two-dimensional Mishra 3 function
Global optimum:  for
for 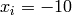 for
for 
Mishra 4 test objective function.
This class defines the Mishra 4 global optimization problem. This is a multimodal minimization problem defined as follows:
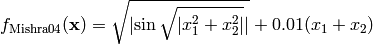
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
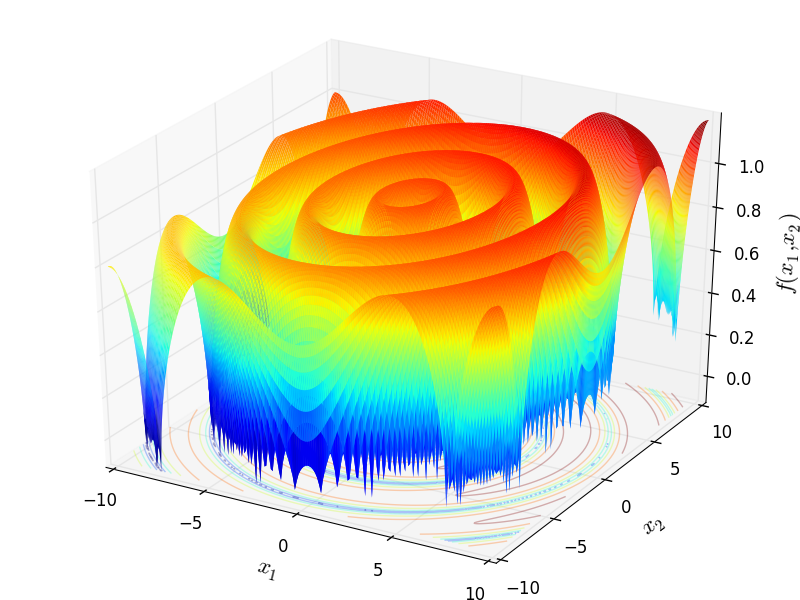
Two-dimensional Mishra 4 function
Global optimum: 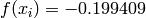 for
for 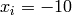 for
for 
Mishra 5 test objective function.
This class defines the Mishra 5 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra05}}(\mathbf{x}) = \left [ \sin^2 ((\cos(x_1) + \cos(x_2))^2) + \cos^2 ((\sin(x_1) + \sin(x_2))^2) + x_1 \right ]^2 + 0.01(x_1 + x_2)](_images/math/876d51fe6b74d7fd64054297bcbd5881794253c9.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
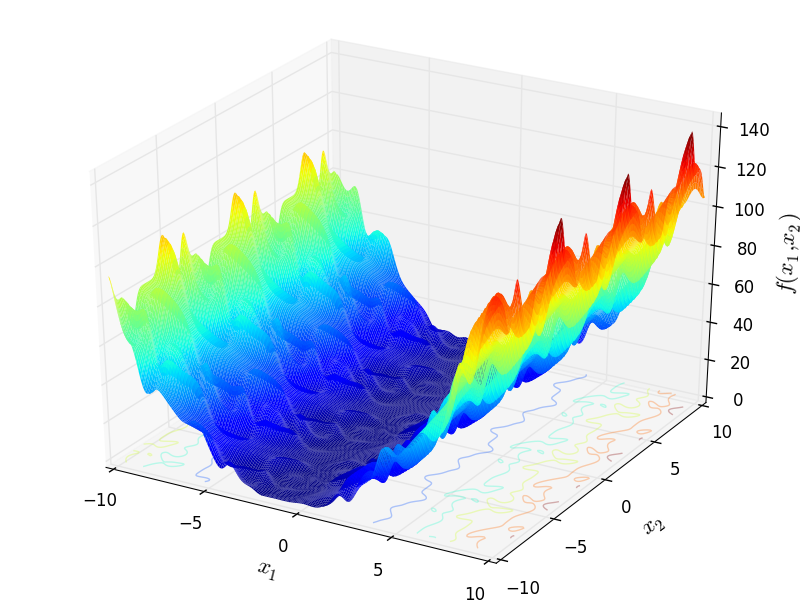
Two-dimensional Mishra 5 function
Global optimum:  for
for ![\mathbf{x} = [-1.98682, -10]](_images/math/2ecafdb455ba5f29d45e3003854ad66015fe5d36.png)
Mishra 6 test objective function.
This class defines the Mishra 6 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra06}}(\mathbf{x}) = -\log{\left [ \sin^2 ((\cos(x_1) + \cos(x_2))^2) - \cos^2 ((\sin(x_1) + \sin(x_2))^2) + x_1 \right ]^2} + 0.01 \left[(x_1 -1)^2 + (x_2 - 1)^2 \right]](_images/math/822c5b71e476eb2b5a19cf1604bf197186a411c4.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
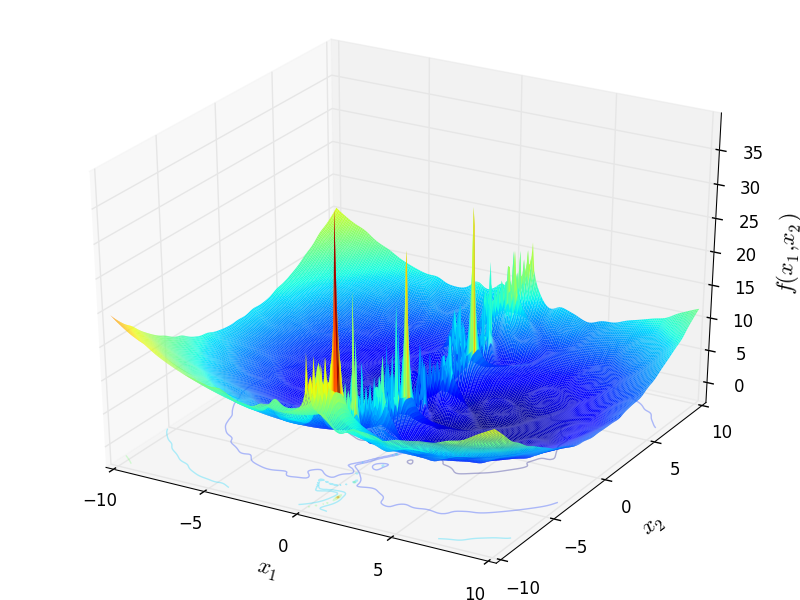
Two-dimensional Mishra 6 function
Global optimum:  for
for ![\mathbf{x} = [2.88631, 1.82326]](_images/math/db37b547caa191433d5a634312b8ab9354fb069e.png)
Mishra 7 test objective function.
This class defines the Mishra 7 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra07}}(\mathbf{x}) = \left [\prod_{i=1}^{n} x_i - n! \right]^2](_images/math/dea6c4fa424bd7f459f3e0ae0371816b77621268.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
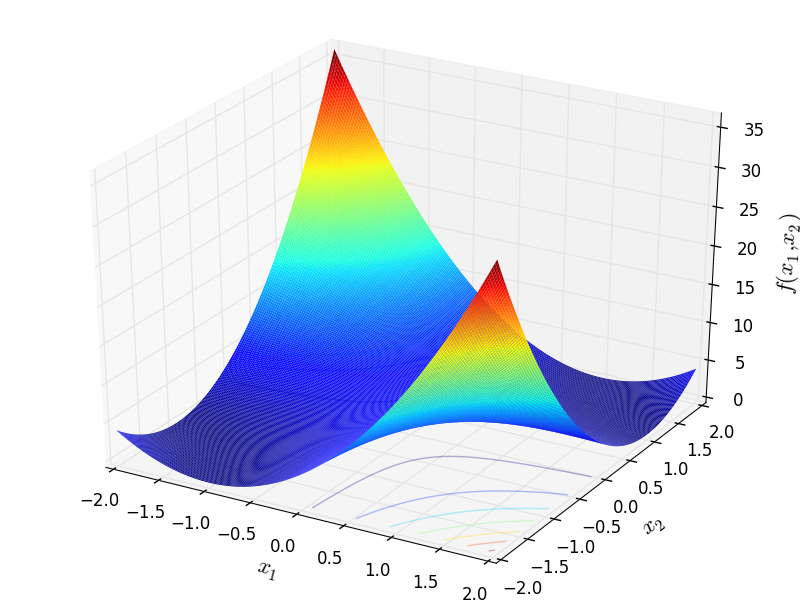
Two-dimensional Mishra 7 function
Global optimum:  for
for  for
for 
Mishra 8 test objective function.
This class defines the Mishra 8 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra08}}(\mathbf{x}) = 0.001 \left[\lvert x_1^{10} - 20x_1^9 + 180x_1^8 - 960 x_1^7 + 3360x_1^6 - 8064x_1^5 + 13340x_1^4 - 15360x_1^3 + 11520x_1^2 - 5120x_1 + 2624 \rvert \lvert x_2^4 + 12x_2^3 + 54x_2^2 + 108x_2 + 81 \rvert \right]^2](_images/math/e4a2b0f328dcfdd8fb8e8b246afb7555d05f19d9.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
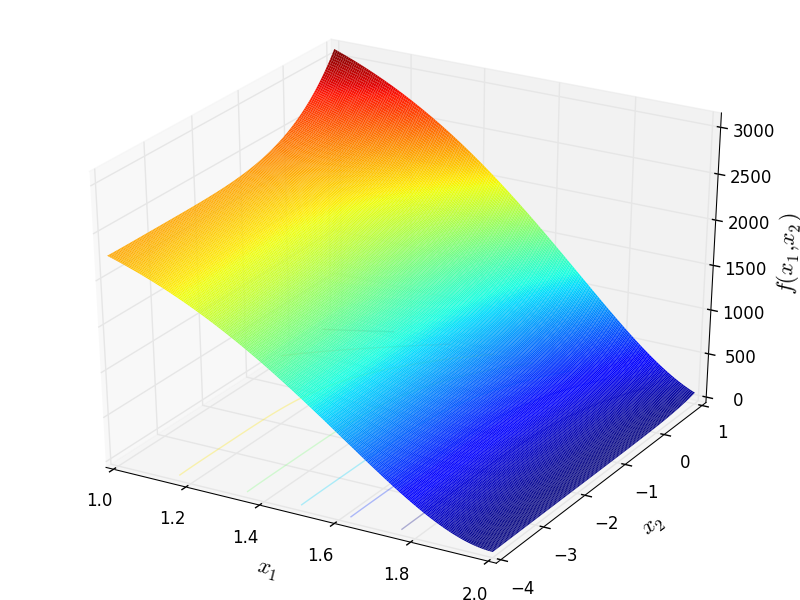
Two-dimensional Mishra 8 function
Global optimum:  for
for ![\mathbf{x} = [2, -3]](_images/math/1927bebccf4c73e04b4474d988813aba0c4c9aa9.png)
Mishra 9 test objective function.
This class defines the Mishra 9 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra09}}(\mathbf{x}) = \left[ ab^2c + abc^2 + b^2 + (x_1 + x_2 - x_3)^2 \right]^2](_images/math/28d97eb34f44e2f2aefe005ffd83925403e1fb01.png)
Where, in this exercise:
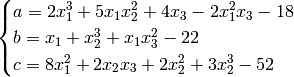
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 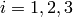 .
.
Global optimum:  for
for ![\mathbf{x} = [1, 2, 3]](_images/math/fdc5c9a7c44dcb0bce4123a6bb782bcbef1c1609.png)
Mishra 10 test objective function.
This class defines the Mishra 10 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra10}}(\mathbf{x}) = \left[ \lfloor x_1 \perp x_2 \rfloor - \lfloor x_1 \rfloor - \lfloor x_2 \rfloor \right]^2](_images/math/bfbc53e18ab8508cb144c76dfa1d510605ead898.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
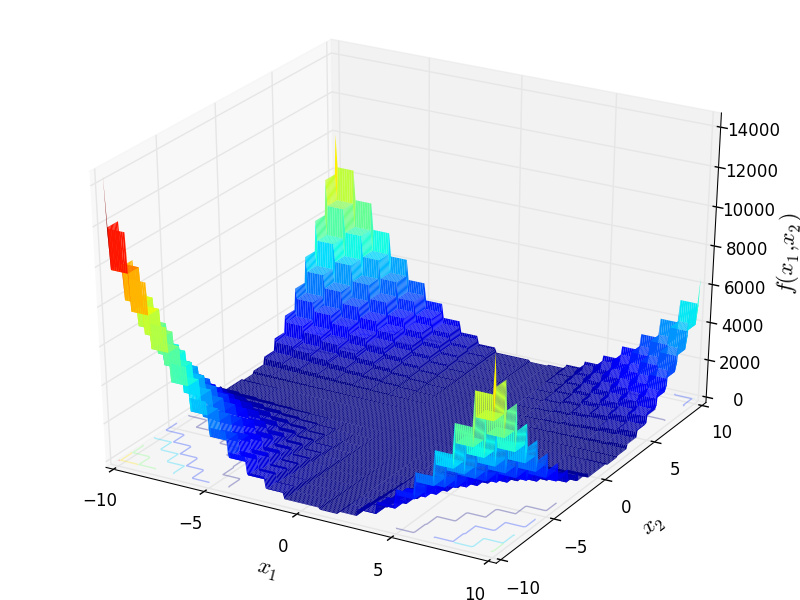
Two-dimensional Mishra 10 function
Global optimum:  for
for ![\mathbf{x} = [2, 2]](_images/math/cd386ccfd141f73b36f03fca835355fe54ed576c.png)
Mishra 11 test objective function.
This class defines the Mishra 11 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Mishra11}}(\mathbf{x}) = \left [ \frac{1}{n} \sum_{i=1}^{n} \lvert x_i \rvert - \left(\prod_{i=1}^{n} \lvert x_i \rvert \right )^{\frac{1}{n}} \right]^2](_images/math/690ba65a511a2e2f3771d926d556c5bcecfb20e8.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
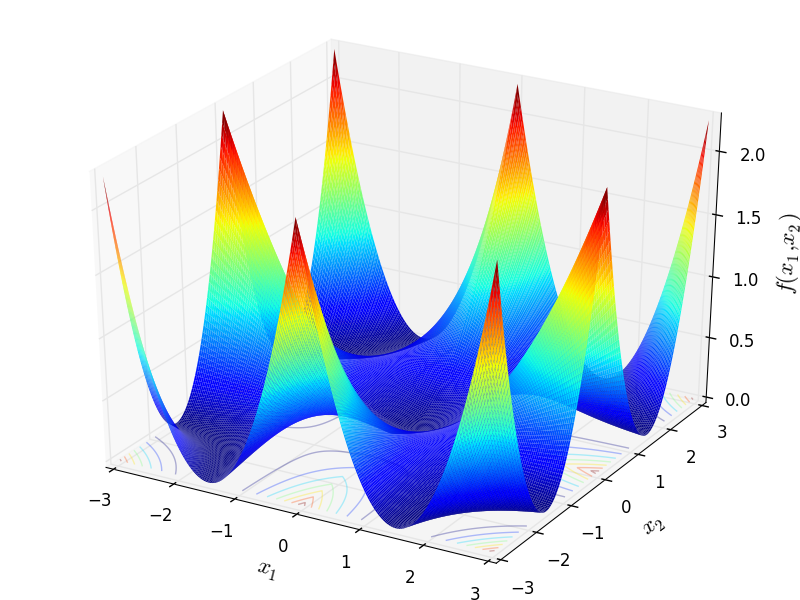
Two-dimensional Mishra 11 function
Global optimum:  for
for 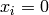 for
for 
MultiModal test objective function.
This class defines the MultiModal global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
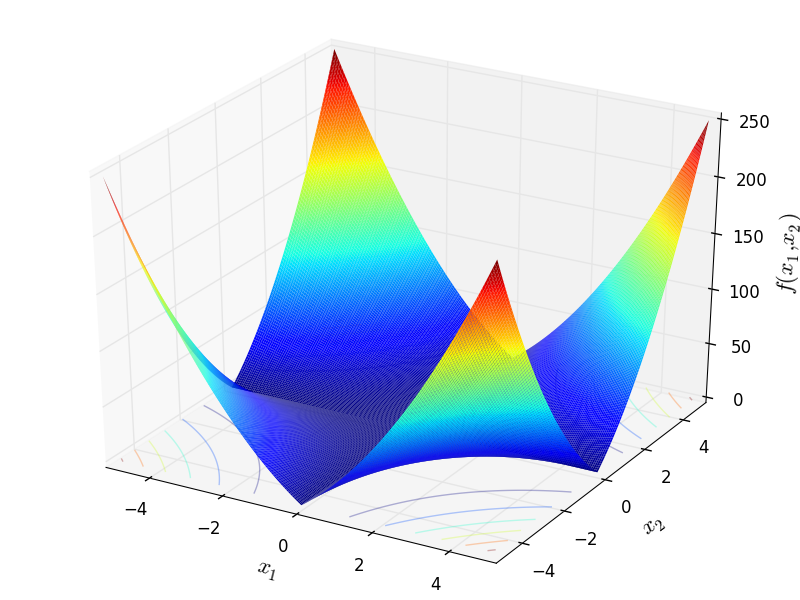
Two-dimensional MultiModal function
Global optimum:  for
for 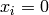 for
for 