 N-D Test Functions L¶
N-D Test Functions L¶Langermann test objective function.
This class defines the Langermann global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Langermann}}(\mathbf{x}) = - \sum_{i=1}^{5} \frac{c_i \cos\left\{\pi \left[\left(x_{1}- a_i\right)^{2} + \left(x_{2} - b_i \right)^{2}\right]\right\}}{e^{\frac{\left( x_{1} - a_i\right)^{2} + \left( x_{2} - b_i\right)^{2}}{\pi}}}](_images/math/594f49ae185e13d3fd0b742b2ac3f81633790223.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
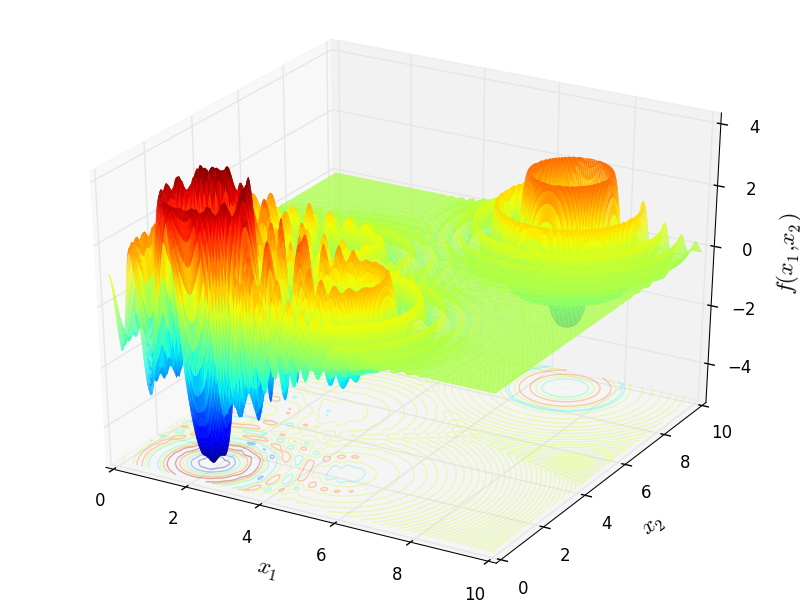
Two-dimensional Langermann function
Global optimum: 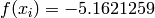 for
for ![\mathbf{x} = [2.00299219, 1.006096]](_images/math/4d8c9390a87c503555d18005da4d9fc0e39976e6.png)
LennardJones test objective function.
This class defines the Lennard-Jones global optimization problem. This is a multimodal minimization problem defined as follows:
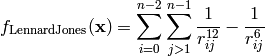
Where, in this exercise:
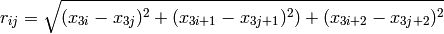
Valid for any dimension, 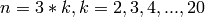 .
.  is the number of atoms in 3-D space
constraints: unconstrained type: multi-modal with one global minimum; non-separable
is the number of atoms in 3-D space
constraints: unconstrained type: multi-modal with one global minimum; non-separable
Value-to-reach: ![minima[k-2] + 0.0001](_images/math/ba1e6d335ea3c9e008913328b1e880949fad3ba5.png) . See array of minima below; additional minima available at
the Cambridge cluster database:
. See array of minima below; additional minima available at
the Cambridge cluster database:
http://www-wales.ch.cam.ac.uk/~jon/structures/LJ/tables.150.html
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-4, 4]](_images/math/8368ca122c49eafe214d1fd60919e78f69b60fc1.png) for
for  .
.
Global optimum:
![minima = [-1.,-3.,-6.,-9.103852,-12.712062,-16.505384,-19.821489,-24.113360, \\
-28.422532,-32.765970,-37.967600,-44.326801,-47.845157,-52.322627, \\
-56.815742,-61.317995, -66.530949,-72.659782,-77.1777043]](_images/math/561e39e42e2aa58f1f7ff7e55d73fad0965b603a.png)
Leon test objective function.
This class defines the Leon global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1.2, 1.2]](_images/math/8665444e183b5eddb24dc54c05ed5e5f7f1f269a.png) for
for  .
.
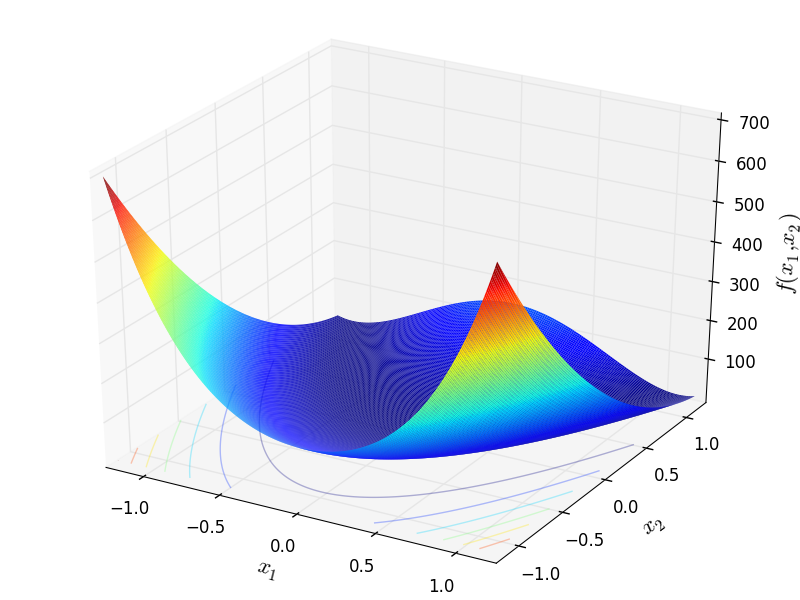
Two-dimensional Leon function
Global optimum:  for
for 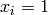 for
for 
Levy 3 test objective function.
This class defines the Levy 3 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Levy03}}(\mathbf{x}) = \sin^2(\pi y_1)+\sum_{i=1}^{n-1}(y_i-1)^2[1+10\sin^2(\pi y_{i+1})]+(y_n-1)^2](_images/math/ede8ef160dbeb592ad23ef62fb2a4d2f6ad446d1.png)
Where, in this exercise:
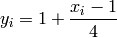
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
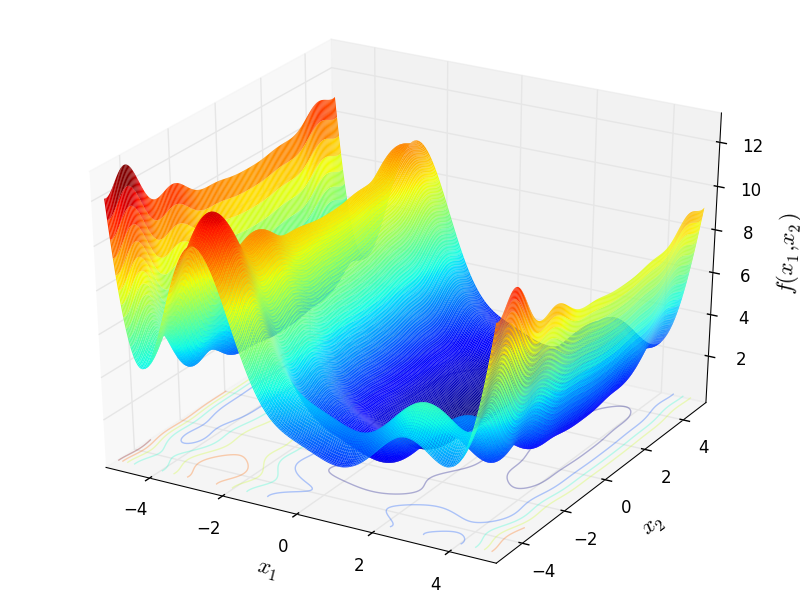
Two-dimensional Levy 3 function
Global optimum:  for
for 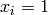 for
for 
Levy 5 test objective function.
This class defines the Levy 5 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Levy05}}(\mathbf{x}) = \sum_{i=1}^{5} i \cos \left[(i-1)x_1 + i \right] \times \sum_{j=1}^{5} j \cos \left[(j+1)x_2 + j \right] + (x_1 + 1.42513)^2 + (x_2 + 0.80032)^2](_images/math/2d94d681bf2dfbe33e12b0368180954e523689b5.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
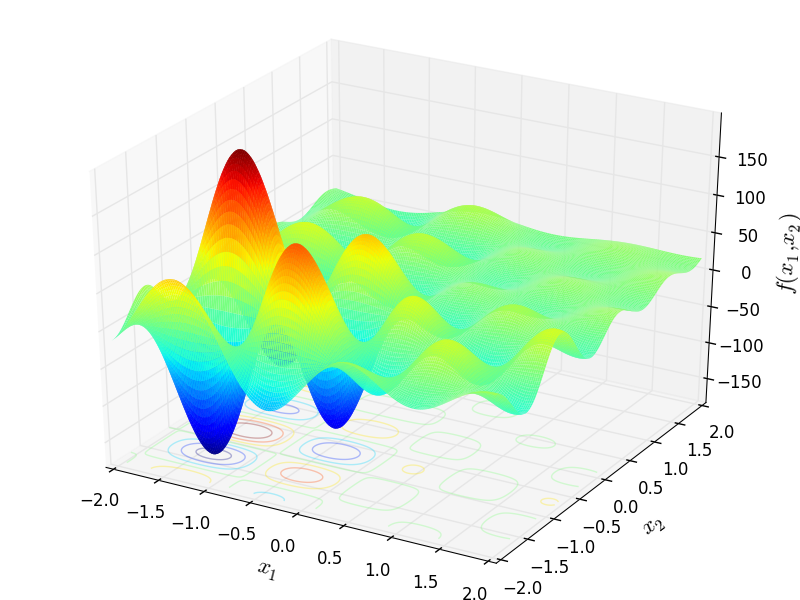
Two-dimensional Levy 5 function
Global optimum:  for
for ![\mathbf{x} = [-1.3068, -1.4248]](_images/math/73f3e5d3ebcf103a196d5b2c8cda8465cff331bf.png) .
.
Levy13 test objective function.
This class defines the Levy13 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Levy13}}(\mathbf{x}) = \left(x_{1} -1\right)^{2} \left[\sin^{2}\left(3 \pi x_{2}\right) + 1\right] + \left(x_{2} -1\right)^{2} \left[\sin^{2}\left(2 \pi x_{2}\right) + 1\right] + \sin^{2}\left(3 \pi x_{1}\right)](_images/math/0bd059389be1db8f08016928127b1695153b4e90.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
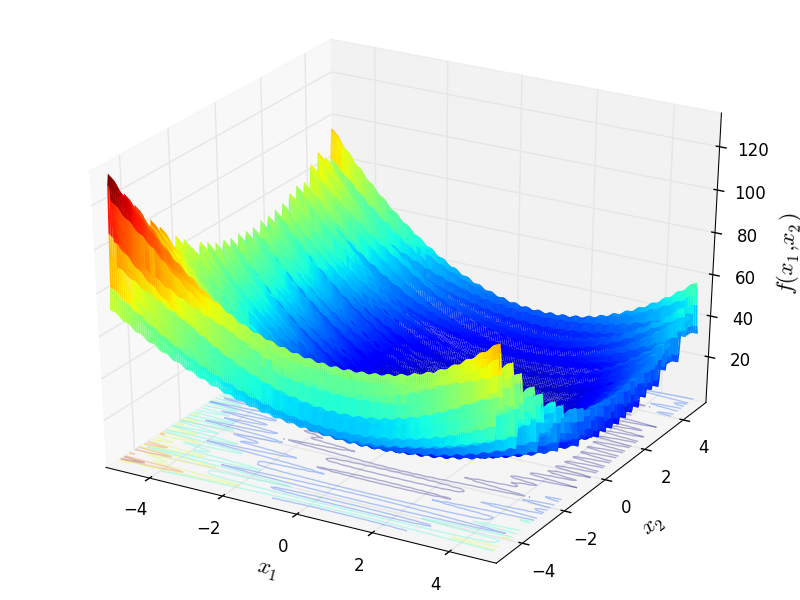
Two-dimensional Levy13 function
Global optimum:  for
for 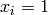 for
for 