Univariate Benchmarks Results

This page shows the results obtained by applying a number of Global optimization algorithms to the entire benchmark suite of 1-D optimization problems, together with some statistics on the algorithm performances.

Note

The CRS2 and DIRECT algorithms from NLOpt did not qualify for the univariate benchmark as I am constantly getting useless ValueError every time I try them.

Note

The CMA-ES algorithm from CMA-ES did not qualify for the univariate benchmark as the Python implementation does not support optimization in 1-D.

Univariate (1D) Test Functions

The following table shows the overall success of all Global Optimization algorithms, considering for every benchmark function 100 random starting points.

So, for example, AMPGO was able to solve, on average, 96.2% of all the test functions for all the 100 random starting points using, on average, 182 functions evaluations.

Optimization algorithms performances (1-dimensional)

Optimization Method	Overall Success (%)	Functions Evaluations
AMPGO	96.222	182
ASA	58.944	318
BasinHopping	71.222	509
DE	88.889	483
Firefly	99.000	490
Galileo	1.556	54
MLSL	13.833	6161
PSWARM	84.222	726
SCE	99.889	105
SIMANN	5.167	1903

These results are also depicted in the next figure, which clearly shows that AMPGO is one of the better-performing optimization algorithms as far as the current benchmark is considered.

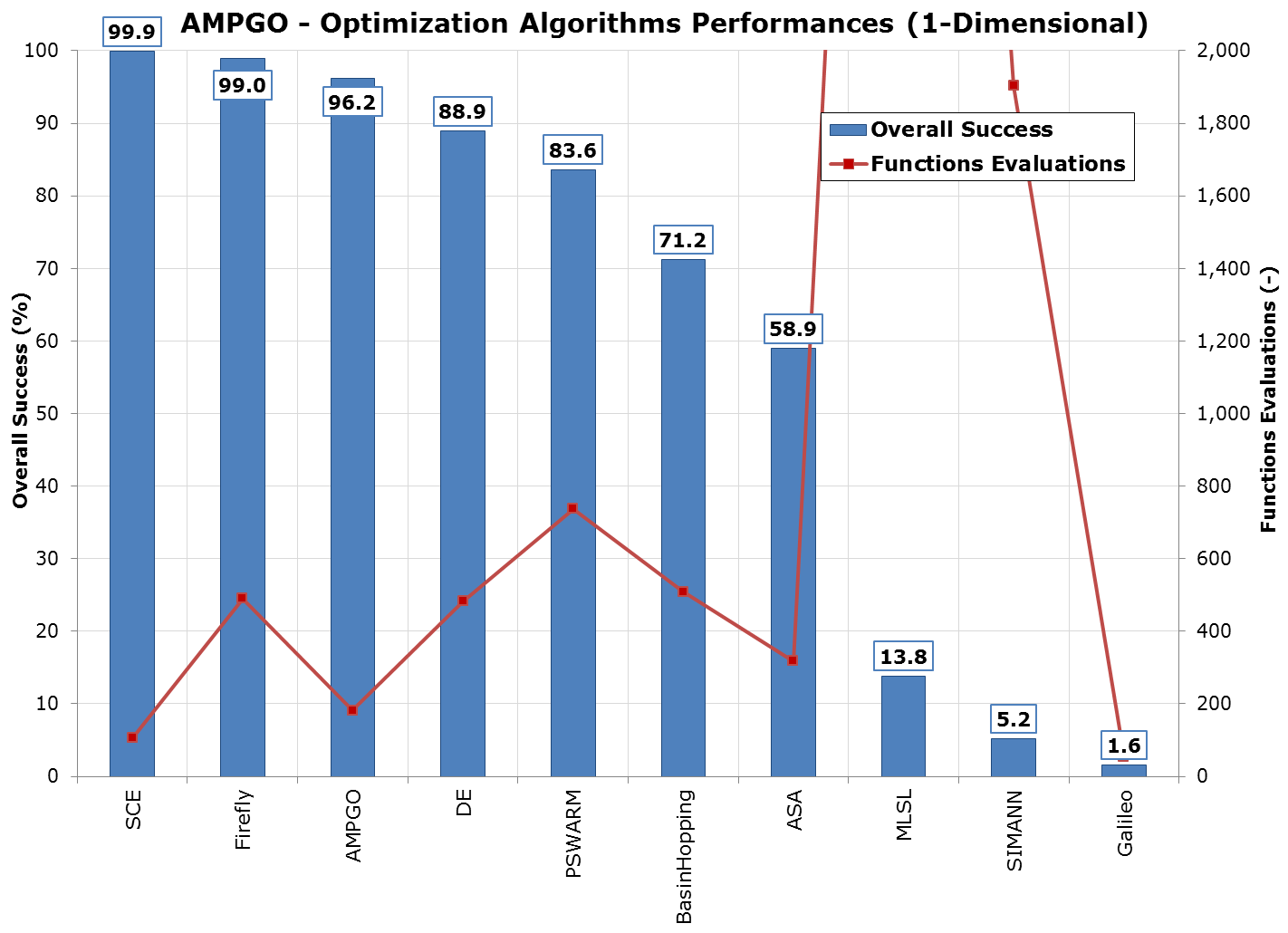
AMPGO Optimization algorithms performances (1-dimensional)

The following table is a split-by-benchmark function of the first table, showing the percentage of successful optimizations per benchmark, considering 100 random starting points.

Optimization algorithms performances (1-dimensional)

Function Name	AMPGO	ASA	BasinHopping	DE	Firefly	Galileo	MLSL	PSWARM	SCE	SIMANN
Problem02	100	100	100	100	99	0	0	100	100	0
Problem03	100	0	43	100	99	0	49	36	100	6
Problem04	100	100	100	100	100	1	0	100	100	1
Problem05	100	99	100	100	96	1	0	100	100	18
Problem06	100	100	32	100	100	2	0	100	100	0
Problem07	100	100	100	100	98	1	0	100	100	1
Problem08	100	0	100	100	100	0	0	26	100	9
Problem09	100	75	41	100	98	0	0	100	100	0
Problem10	88	0	36	0	100	0	0	100	100	17
Problem11	100	100	82	100	100	2	0	65	100	0
Problem12	100	0	81	100	100	4	100	46	100	0
Problem13	100	100	100	100	100	8	0	100	100	4
Problem14	100	100	84	100	99	1	0	100	100	1
Problem15	100	100	54	100	100	5	0	100	100	0
Problem18	100	87	100	100	100	1	100	100	100	0
Problem20	100	0	36	100	100	0	0	100	100	0
Problem21	43	0	24	100	100	1	0	100	100	32
Problem22	100	0	67	0	93	0	0	43	98	0

The following table is a split-by-benchmark function of the first table, showing the average number of functions evaluations for successful optimizations only, considering 100 random starting points.

Optimization algorithms performances (1-dimensional)

Function Name	AMPGO	ASA	BasinHopping	DE	Firefly	Galileo	MLSL	PSWARM	SCE	SIMANN
Problem02	38	296	671	235	509	51	7303	194	77	2001
Problem03	254	–	400	469	939	56	3909	2360	265	1283
Problem04	6	340	511	246	219	52	7341	167	44	2000
Problem05	116	323	732	92	477	56	7026	360	126	1945
Problem06	145	310	256	323	604	54	7294	309	76	2001
Problem07	47	322	640	279	397	53	7419	214	65	1997
Problem08	138	–	766	283	915	58	5254	2579	252	1251
Problem09	66	316	443	224	541	57	7289	291	124	2001
Problem10	543	–	533	2005	553	55	7554	211	74	1944
Problem11	17	316	507	905	482	56	6647	1296	93	2001
Problem12	120	–	584	190	419	46	59	1737	87	2001
Problem13	7	334	722	169	150	55	7450	174	36	1996
Problem14	67	302	637	257	185	58	6977	293	104	2000
Problem15	51	325	411	286	218	57	7897	201	46	2001
Problem18	5	321	354	1730	420	57	191	180	59	2001
Problem20	89	–	259	428	379	52	7233	274	67	2001
Problem21	1545	–	272	356	722	51	7314	197	79	1843
Problem22	25	–	472	223	708	55	6743	2046	216	2001