 N-D Test Functions G¶
N-D Test Functions G¶Gear test objective function.
This class defines the Gear global optimization problem. This is a multimodal minimization problem defined as follows:
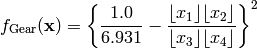
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [12, 60]](_images/math/dede825b8eb6d5fc4458fe32630b03f0e24b49f1.png) for
for  .
.
Global optimum:  for
for ![\mathbf{x} = [16, 19, 43, 49]](_images/math/ff60dadef62a5b6f9030bf858fc411f15672edb1.png) , where the various
, where the various
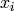 may be permuted.
may be permuted.
Giunta test objective function.
This class defines the Giunta global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Giunta}}(\mathbf{x}) = 0.6 + \sum_{i=1}^{n} \left[\sin^{2}\left(1 - \frac{16}{15} x_i\right) - \frac{1}{50} \sin\left(4 - \frac{64}{15} x_i\right) - \sin\left(1 - \frac{16}{15} x_i\right)\right]](_images/math/4f94e6fac92562b0bb497a09e7087ed756ca30ff.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
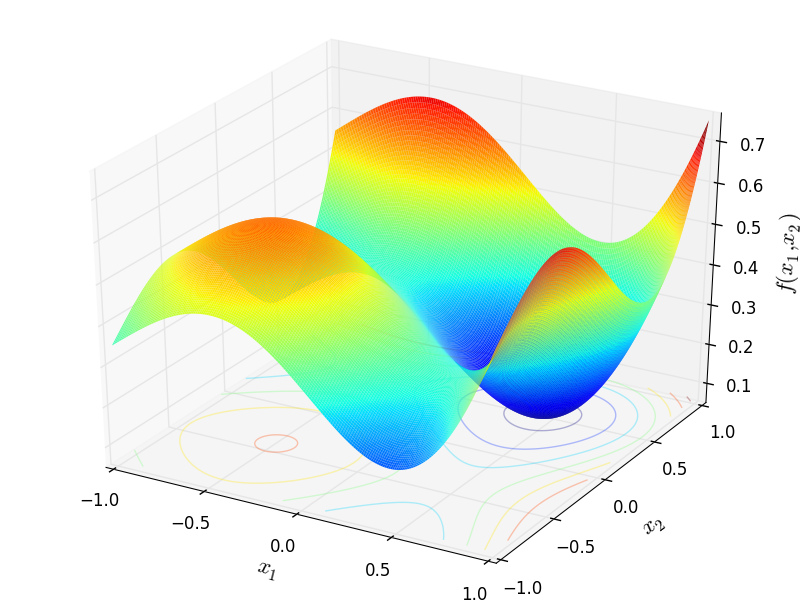
Two-dimensional Giunta function
Global optimum: 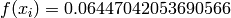 for
for ![\mathbf{x} = [0.4673200277395354, 0.4673200169591304]](_images/math/458f23f04ef9f66ab15404a755124ad3dbded63a.png)
Goldstein-Price test objective function.
This class defines the Goldstein-Price global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{GoldsteinPrice}}(\mathbf{x}) = \left[ 1+(x_1+x_2+1)^2(19-14x_1+3x_1^2-14x_2+6x_1x_2+3x_2^2) \right] \left[ 30+(2x_1-3x_2)^2(18-32x_1+12x_1^2+48x_2-36x_1x_2+27x_2^2) \right]](_images/math/62e850b32ec9dcf39e20f8b8a1bd11b074e6ced0.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-2, 2]](_images/math/3220cc226a0abf06f00e70257db97b5c754120f7.png) for
for  .
.
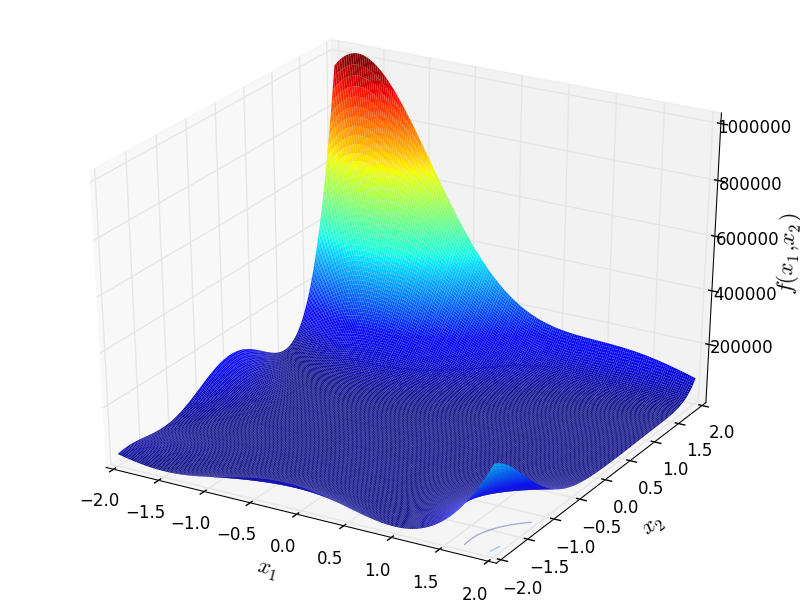
Two-dimensional Goldstein-Price function
Global optimum: 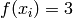 for
for ![\mathbf{x} = [0, -1]](_images/math/b1a4998088c07bbc6ec2c94d0e59f3f49c3e4fc1.png)
Griewank test objective function.
This class defines the Griewank global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-600, 600]](_images/math/0e2220a1d45e6496e4278b9191e14b72dbf2da2b.png) for
for  .
.
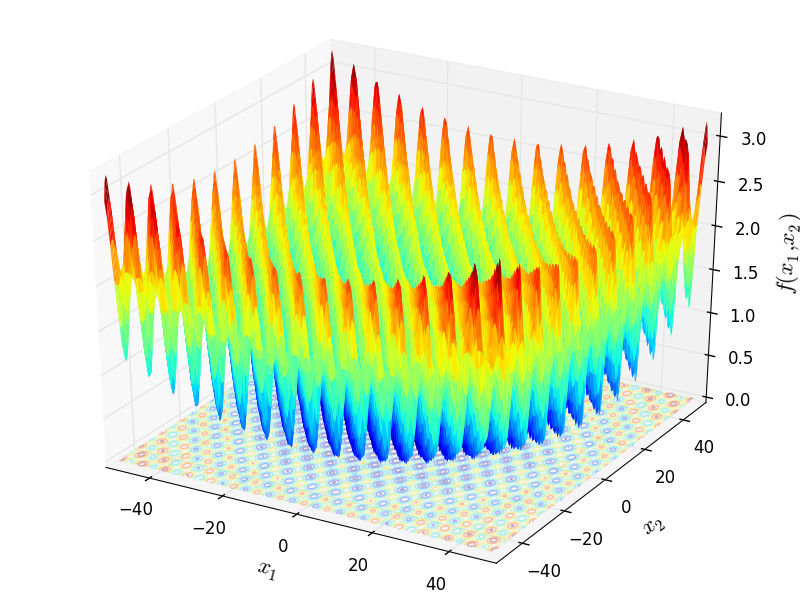
Two-dimensional Griewank function
Global optimum:  for
for 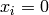 for
for 
Gulf test objective function.
This class defines the Gulf global optimization problem. This is a multimodal minimization problem defined as follows:
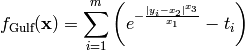
Where, in this exercise:
![t_i = i/100 \\
y_i = 25 + [-50 \log(t_i)]^{2/3}](_images/math/a38ad5fb61dee8c6ed344e687aa89bd226d15066.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 60]](_images/math/96a3ee6ecb764ba6669d36899fea5c563488b3f5.png) for
for 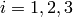 .
.
Global optimum:  for
for ![\mathbf{x} = [50, 25, 1.5]](_images/math/213fecbadfdaff832486b641e83587ac11937340.png)