 N-D Test Functions D¶
N-D Test Functions D¶Damavandi test objective function.
This class defines the Damavandi global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Damavandi}}(\mathbf{x}) = \left[ 1 - \lvert{\frac{\sin[\pi(x_1-2)]\sin[\pi(x2-2)]}{\pi^2(x_1-2)(x_2-2)}} \rvert^5 \right] \left[2 + (x_1-7)^2 + 2(x_2-7)^2 \right]](_images/math/59e99680fe1ed9013c347e02260ef958abc04e28.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 14]](_images/math/86868132f68d740331d535e78dfc1543ea16b982.png) for
for  .
.
Two-dimensional Damavandi function
Global optimum:  for
for 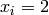 for
for 
Deb 1 test objective function.
This class defines the Deb 1 global optimization problem. This is a multimodal minimization problem defined as follows:
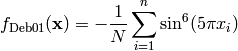
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for  .
.
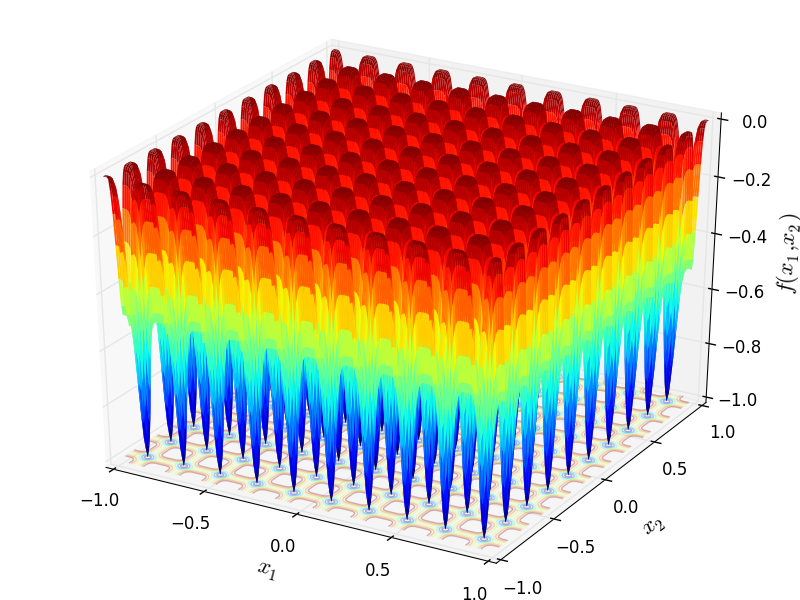
Two-dimensional Deb 1 function
Global optimum:  . The number of global minima is
. The number of global minima is 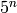 that are evenly spaced
in the function landscape, where
that are evenly spaced
in the function landscape, where  represents the dimension of the problem.
represents the dimension of the problem.
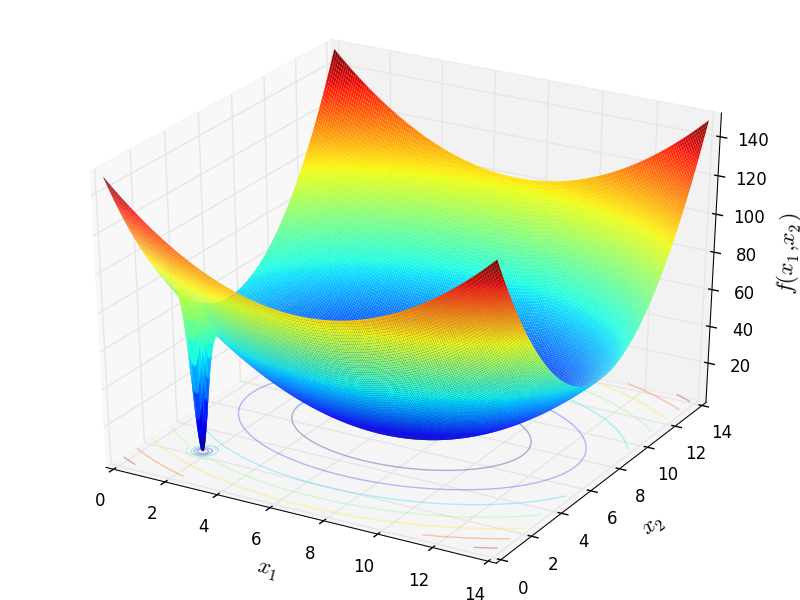
Deb 2 test objective function.
This class defines the Deb 2 global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Deb02}}(\mathbf{x}) = - \frac{1}{N} \sum_{i=1}^n \sin^6 \left[ 5 \pi \left ( x_i^{3/4} - 0.05 \right) \right ]](_images/math/e805a425965a8313cac84c520ae187bc19d805f3.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
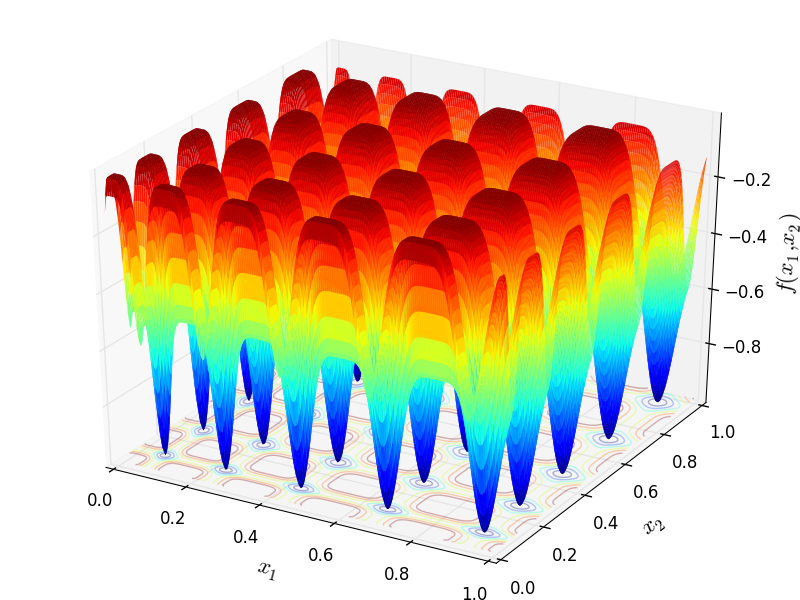
Two-dimensional Deb 2 function
Global optimum:  . The number of global minima is
. The number of global minima is 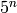 that are evenly spaced
in the function landscape, where
that are evenly spaced
in the function landscape, where  represents the dimension of the problem.
represents the dimension of the problem.
Decanomial test objective function.
This class defines the Decanomial function global optimization problem. This is a multimodal minimization problem defined as follows:
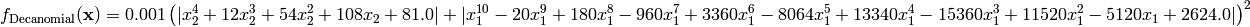
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
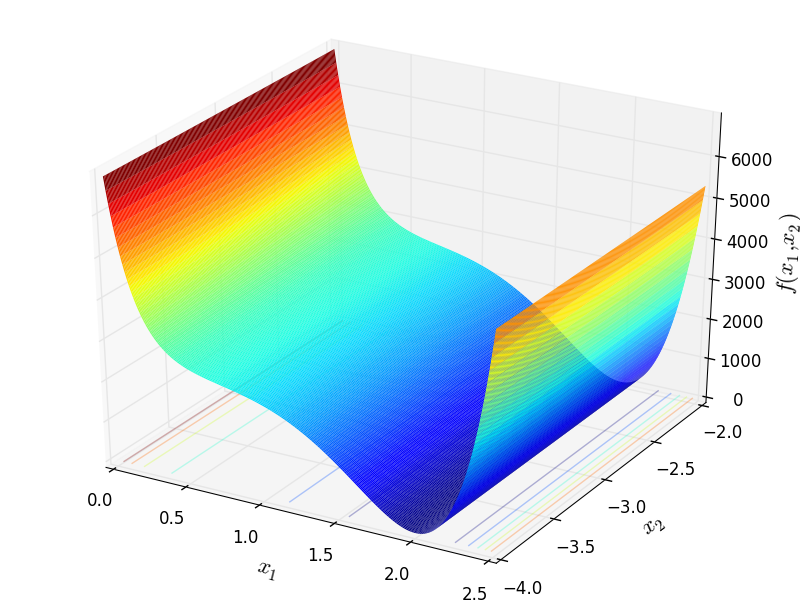
Two-dimensional Decanomial function
Global optimum:  for
for ![\mathbf{x} = [2, -3]](_images/math/1927bebccf4c73e04b4474d988813aba0c4c9aa9.png)
Deceptive test objective function.
This class defines the Deceptive global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Deceptive}}(\mathbf{x}) = - \left [\frac{1}{n} \sum_{i=1}^{n} g_i(x_i) \right ]^{\beta}](_images/math/1d2692f89270d5498fa2f9c2c61e0174e3fe5c69.png)
Where 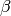 is a fixed non-linearity factor; in this exercise,
is a fixed non-linearity factor; in this exercise, 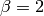 . The function
. The function 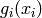 is given by:
is given by:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 1]](_images/math/e365bfdf2ca5275ec86c322fa2fe576a37b0efd7.png) for
for  .
.
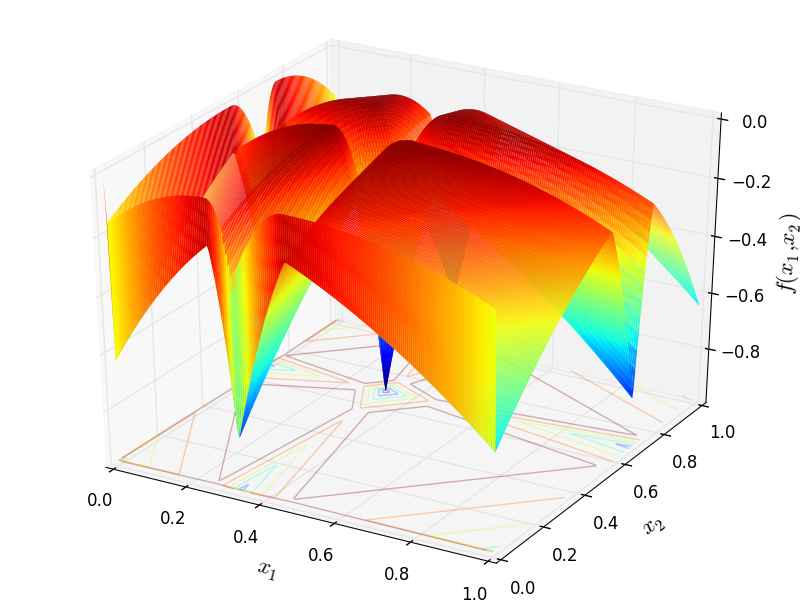
Two-dimensional Deceptive function
Global optimum:  for
for  for
for 
Deckkers-Aarts test objective function.
This class defines the Deckkers-Aarts global optimization problem. This is a multimodal minimization problem defined as follows:
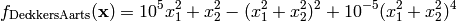
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-20, 20]](_images/math/026a917a812dbaef4e7a8ea87e9963bb111e2644.png) for
for  .
.
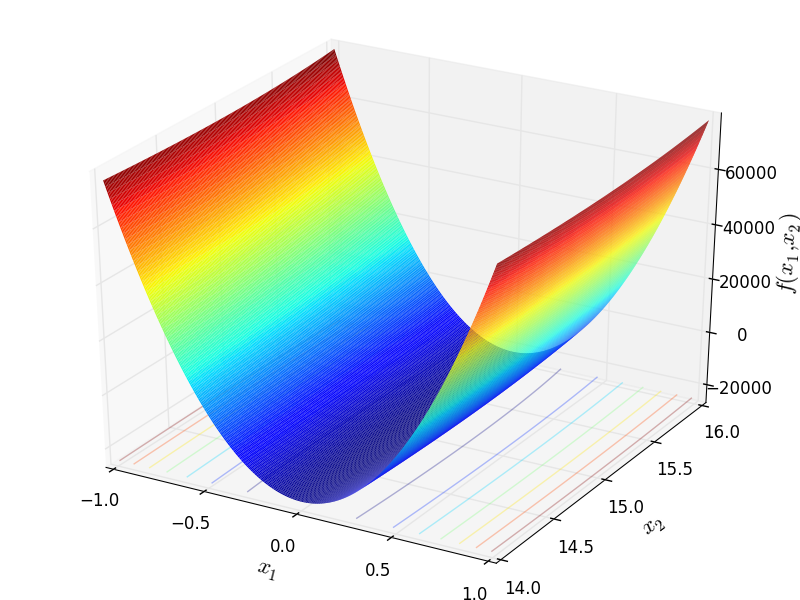
Two-dimensional Deckkers-Aarts function
Global optimum:  for
for ![\mathbf{x} = [0, \pm 15]](_images/math/b00a160fef1130b2b3343e62c8d2e18ca60cde1b.png)
DeflectedCorrugatedSpring test objective function.
This class defines the Deflected Corrugated Spring function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeflectedCorrugatedSpring}}(\mathbf{x}) = 0.1\sum_{i=1}^n \left[ (x_i - \alpha)^2 - \cos \left( K \sqrt {\sum_{i=1}^n (x_i - \alpha)^2} \right ) \right ]](_images/math/13f0611b18cacd4e77a50aeac7e181fd8c9c349f.png)
Where, in this exercise, 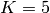 and
and  .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 2\alpha]](_images/math/815ec82f0857513643b0218418ff034b4c03c303.png) for
for  .
.
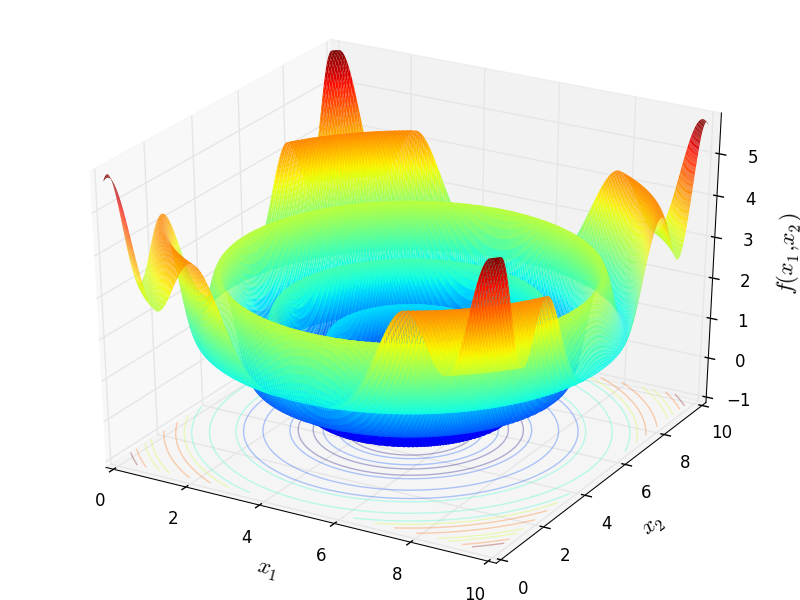
Two-dimensional Deflected Corrugated Spring function
Global optimum:  for
for  for
for 
DeVilliers-Glasser 1 test objective function.
This class defines the DeVilliers-Glasser 1 function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeVilliersGlasser01}}(\mathbf{x}) = \sum_{i=1}^{24} \left[ x_1x_2^{t_i} \sin(x_3t_i + x_4) - y_i \right ]^2](_images/math/752febdbe7a8a79b7354e37dd9b02c74cf88625d.png)
Where, in this exercise, 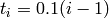 and
and 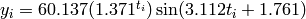 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [1, 100]](_images/math/6ac9e2288bc341c91167d5776d1ce332f99c9f0a.png) for
for  .
.
Global optimum:  for
for 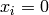 for
for ![\mathbf{x} = [60.137, 1.371, 3.112, 1.761]](_images/math/a85be38e5004238edd2eb5191f90c470c73f7dd3.png) .
.
DeVilliers-Glasser 2 test objective function.
This class defines the DeVilliers-Glasser 2 function global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{DeVilliersGlasser01}}(\mathbf{x}) = \sum_{i=1}^{24} \left[ x_1x_2^{t_i} \tanh \left [x_3t_i + \sin(x_4t_i) \right] \cos(t_ie^{x_5}) - y_i \right ]^2](_images/math/f38ea409192e51399483cfa39e219173f3c12a67.png)
Where, in this exercise, 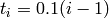 and
and 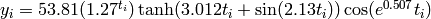 .
.
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [1, 60]](_images/math/0114664ceb945a0b71437326111ea53c01e8607e.png) for
for  .
.
Global optimum:  for
for 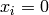 for
for ![\mathbf{x} = [53.81, 1.27, 3.012, 2.13, 0.507]](_images/math/a91b77d2cd0bab7045a92e22ccd6a936e9ce10cd.png) .
.
Dixon and Price test objective function.
This class defines the Dixon and Price global optimization problem. This is a multimodal minimization problem defined as follows:
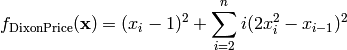
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
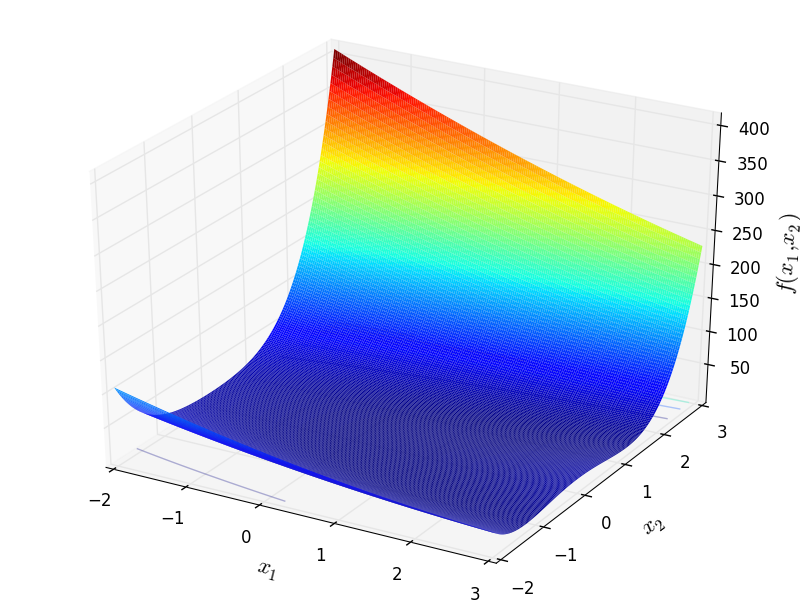
Two-dimensional Dixon and Price function
Global optimum:  for
for  for
for 
Dolan test objective function.
This class defines the Dolan global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
Global optimum: 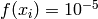 for
for ![\mathbf{x} = [8.39045925, 4.81424707, 7.34574133, 68.88246895, 3.85470806]](_images/math/419c44ff3797c4b8beac8b178fe8c691a80f5e74.png)
DropWave test objective function.
This class defines the DropWave global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5.12, 5.12]](_images/math/670fd074f4bb495bf2a1d327d769de738121e329.png) for
for  .
.

Two-dimensional DropWave function
Global optimum:  for
for 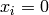 for
for 