 N-D Test Functions C¶
N-D Test Functions C¶CarromTable test objective function.
This class defines the CarromTable global optimization problem. This is a multimodal minimization problem defined as follows:
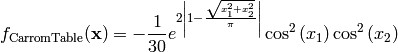
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
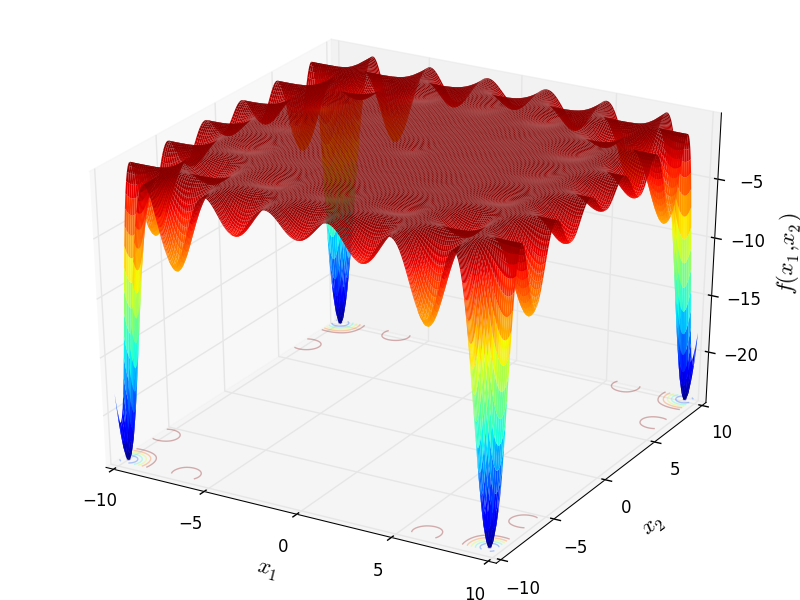
Two-dimensional CarromTable function
Global optimum:  for
for  for
for 
Chichinadze test objective function.
This class defines the Chichinadze global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-30, 30]](_images/math/292d5c0e898bdbf6ba6ae08a62a7750af442c17a.png) for
for  .
.
Two-dimensional Chichinadze function
Global optimum: 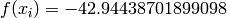 for
for ![\mathbf{x} = [6.189866586965680, 0.5]](_images/math/5f05f88427975a946afc3cd8c5370fc8c0cef4e2.png)
Cigar test objective function.
This class defines the Cigar global optimization problem. This is a multimodal minimization problem defined as follows:
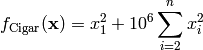
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-100, 100]](_images/math/33bdb423b6ec61d9668e76b556c95c96b2bb72ef.png) for
for  .
.
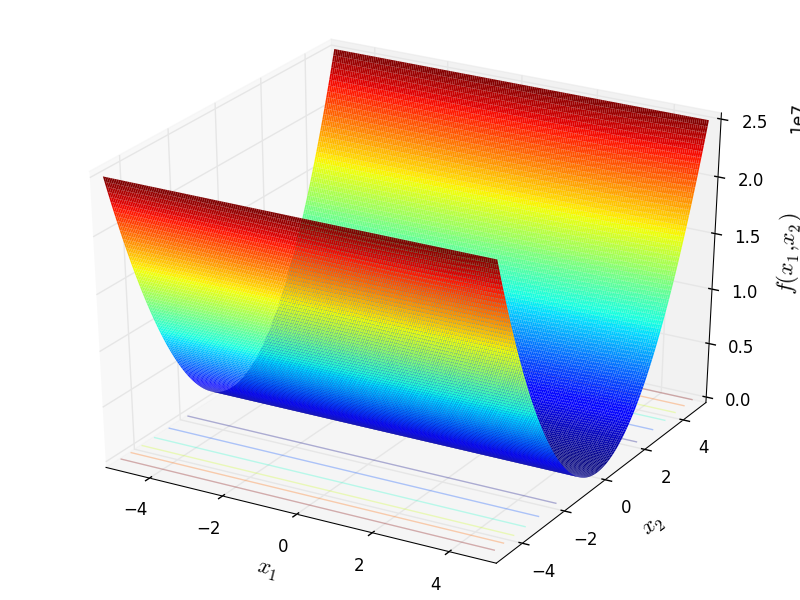
Two-dimensional Cigar function
Global optimum:  for
for  for
for 
Cola test objective function.
This class defines the Cola global optimization problem. The 17-dimensional function computes
indirectly the formula 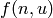 by setting
by setting 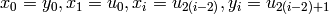 :
:
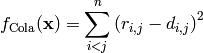
Where 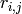 is given by:
is given by:

And  is a symmetric matrix given by:
is a symmetric matrix given by:
![\mathbf{d} = \left [ d_{ij} \right ] = \begin{pmatrix}
1.27 & & & & & & & & \\
1.69 & 1.43 & & & & & & & \\
2.04 & 2.35 & 2.43 & & & & & & \\
3.09 & 3.18 & 3.26 & 2.85 & & & & & \\
3.20 & 3.22 & 3.27 & 2.88 & 1.55 & & & & \\
2.86 & 2.56 & 2.58 & 2.59 & 3.12 & 3.06 & & & \\
3.17 & 3.18 & 3.18 & 3.12 & 1.31 & 1.64 & 3.00 & \\
3.21 & 3.18 & 3.18 & 3.17 & 1.70 & 1.36 & 2.95 & 1.32 & \\
2.38 & 2.31 & 2.42 & 1.94 & 2.85 & 2.81 & 2.56 & 2.91 & 2.97
\end{pmatrix}](_images/math/ff0c1fb88112b9fb6d119f6999d2add82f8ae22b.png)
This function has bounds  and
and 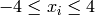 for
for 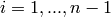 . It
has a global minimum of 11.7464.
. It
has a global minimum of 11.7464.
Colville test objective function.
This class defines the Colville global optimization problem. This is a multimodal minimization problem defined as follows:
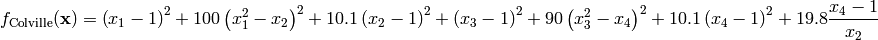
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
Global optimum:  for
for 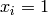 for
for 
Corana test objective function.
This class defines the Corana global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Corana}}(\mathbf{x}) = \begin{cases} \sum_{i=1}^n 0.15 d_i [z_i - 0.05\textrm{sgn}(z_i)]^2 & \textrm{if}|x_i-z_i| < 0.05 \\
d_ix_i^2 & \textrm{otherwise}\end{cases}](_images/math/f26b4f4f9ba4603649e6e8cfcc4c69071165b69d.png)
Where, in this exercise:
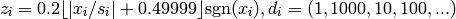
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-5, 5]](_images/math/b7a53fa3c9c2f313c2a86c222fdfbbeaf4b5a3ed.png) for
for  .
.
Global optimum:  for
for  for
for 
Cosine Mixture test objective function.
This class defines the Cosine Mixture global optimization problem. This is a multimodal minimization problem defined as follows:
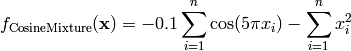
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for 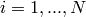 .
.
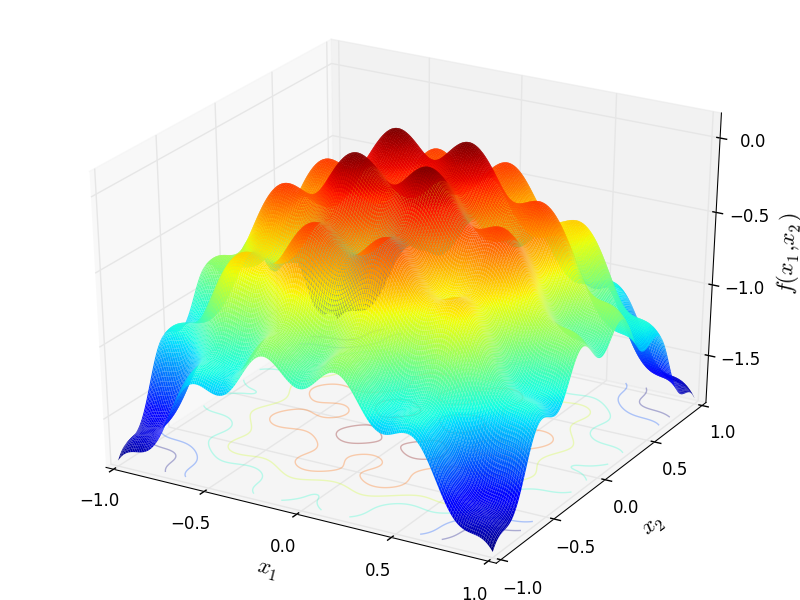
Two-dimensional Cosine Mixture function
Global optimum: 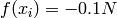 for
for  for
for 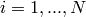
Cross-in-Tray test objective function.
This class defines the Cross-in-Tray global optimization problem. This is a multimodal minimization problem defined as follows:
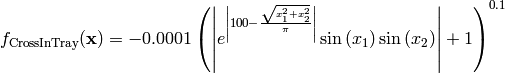
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-15, 15]](_images/math/fca9e26666540be67aae472b6068981e5e8b1471.png) for
for  .
.
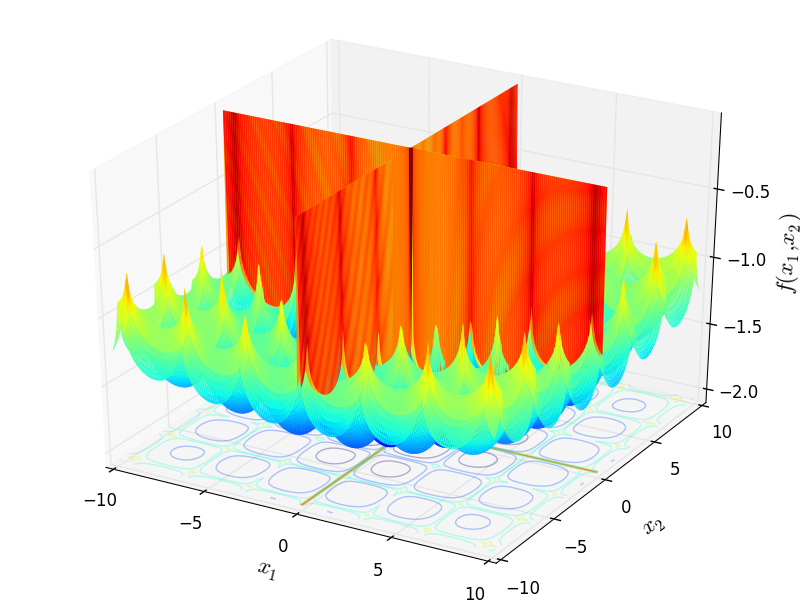
Two-dimensional Cross-in-Tray function
Global optimum: 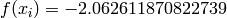 for
for 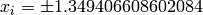 for
for 
Cross-Leg-Table test objective function.
This class defines the Cross-Leg-Table global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
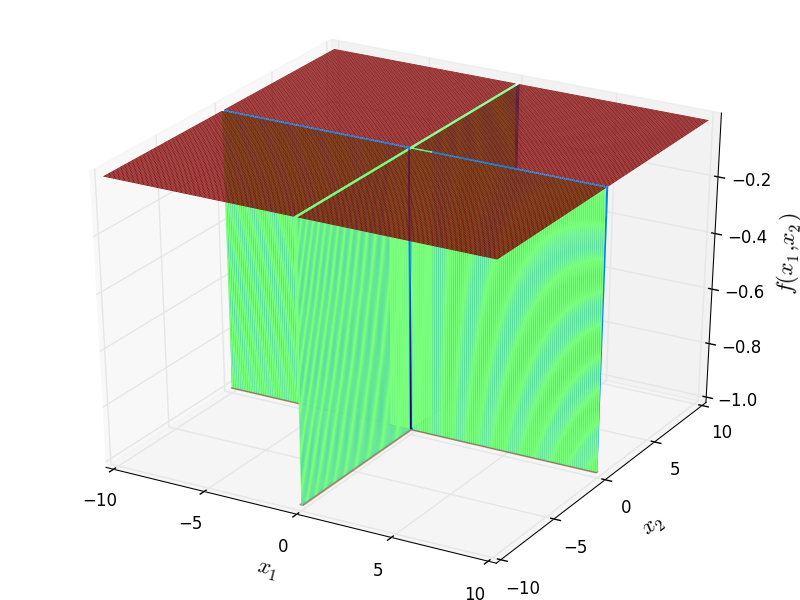
Two-dimensional Cross-Leg-Table function
Global optimum:  . The global minimum is found on the planes
. The global minimum is found on the planes  and
and 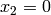
Crowned Cross test objective function.
This class defines the Crowned Cross global optimization problem. This is a multimodal minimization problem defined as follows:
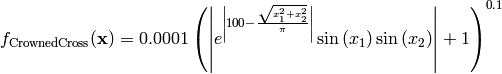
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
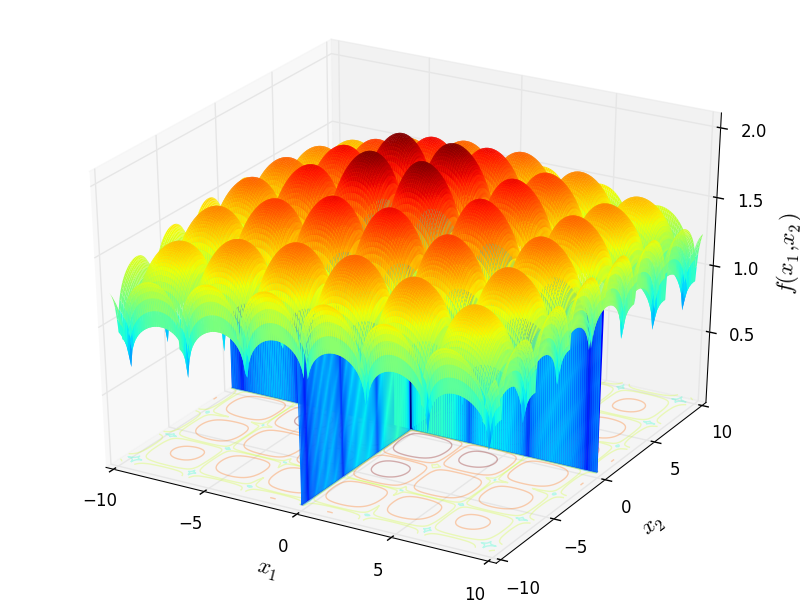
Two-dimensional Crowned Cross function
Global optimum: 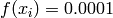 . The global minimum is found on the planes
. The global minimum is found on the planes  and
and 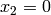
Csendes test objective function.
This class defines the Csendes global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{Csendes}}(\mathbf{x}) = \sum_{i=1}^n x_i^6 \left[ 2 + \sin \left( \frac{1}{x_i} \right ) \right]](_images/math/6650d8daa1463524b982efd049240b36a7c8a193.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-1, 1]](_images/math/69d20098894c45659a72bd07f85a904ff6726b1e.png) for
for 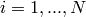 .
.
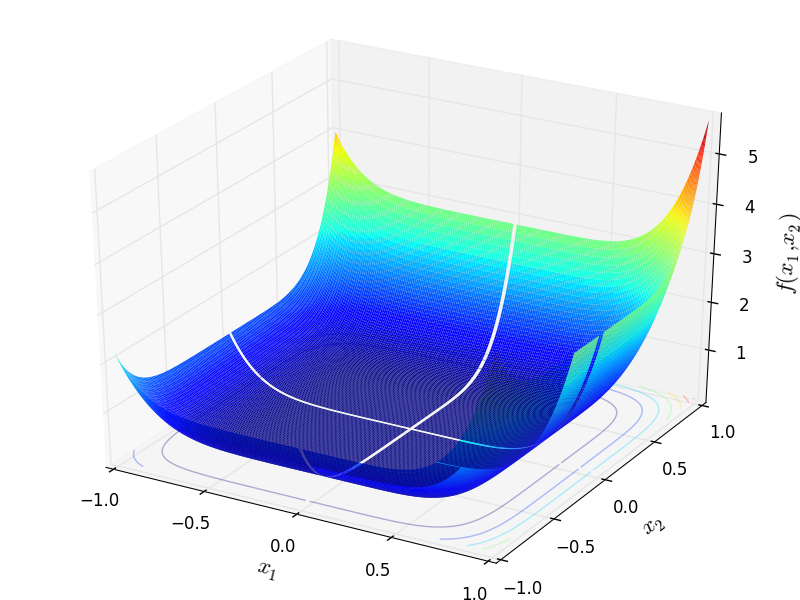
Two-dimensional Csendes function
Global optimum:  for
for  for
for 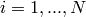
Cube test objective function.
This class defines the Cube global optimization problem. This is a multimodal minimization problem defined as follows:
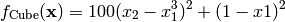
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for 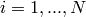 .
.

Two-dimensional Cube function
Global optimum:  for
for ![\mathbf{x} = [1, 1]](_images/math/7dafdca30782528518941cafca8f36e16afc0d35.png)