 N-D Test Functions A¶
N-D Test Functions A¶Ackley test objective function.
This class defines the Ackley global optimization problem. This is a multimodal minimization problem defined as follows:
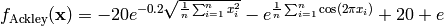
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-32, 32]](_images/math/b256b356be385a92f6c093826bbb33b853901a6f.png) for
for  .
.
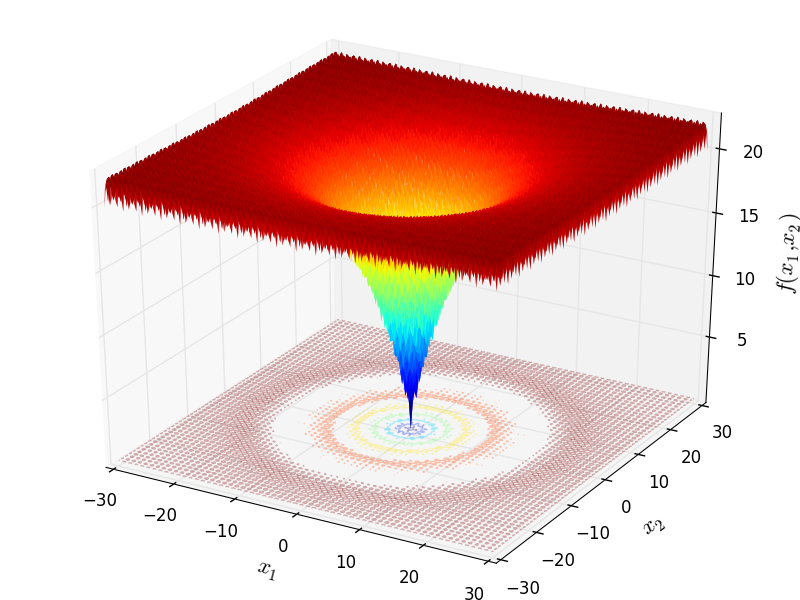
Two-dimensional Ackley function
Global optimum:  for
for 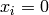 for
for 
Adjiman test objective function.
This class defines the Adjiman global optimization problem. This is a multimodal minimization problem defined as follows:
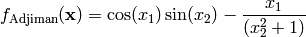
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_1 \in [-1, 2]](_images/math/0e209e5911bcd73df39efe5dd208eaa7d9562260.png) and
and ![x_2 \in [-1, 1]](_images/math/68d67d873e4f24bdfcd8f0a26d9caffd834d8dfb.png) .
.
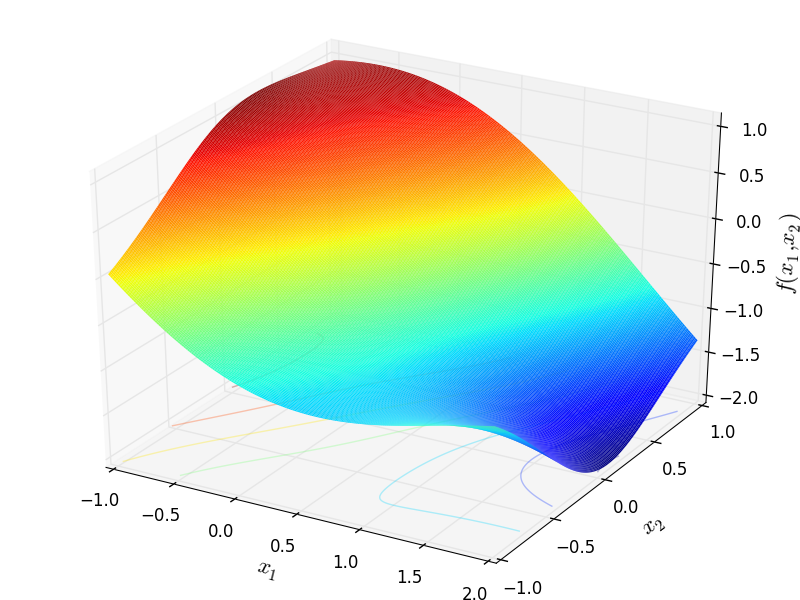
Two-dimensional Adjiman function
Global optimum: 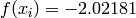 for
for ![\mathbf{x} = [2, 0.10578]](_images/math/162fe2f9f814004562f383067e4c225a4f0dd09c.png)
Alpine 1 test objective function.
This class defines the Alpine 1 global optimization problem. This is a multimodal minimization problem defined as follows:
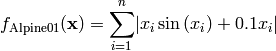
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [-10, 10]](_images/math/d511ca3206c16bae3e3af3c02835f3fe9fb07286.png) for
for  .
.
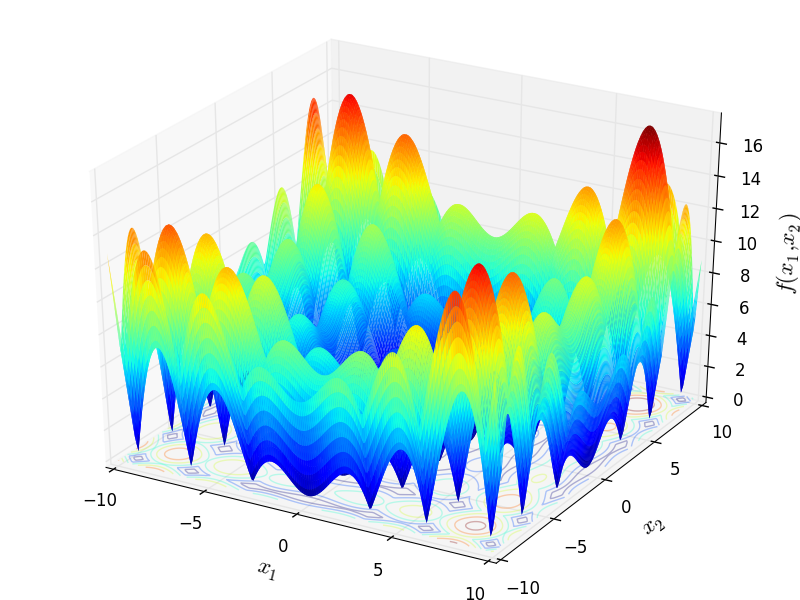
Two-dimensional Alpine 1 function
Global optimum:  for
for 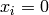 for
for 
Alpine 2 test objective function.
This class defines the Alpine 2 global optimization problem. This is a multimodal minimization problem defined as follows:

Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
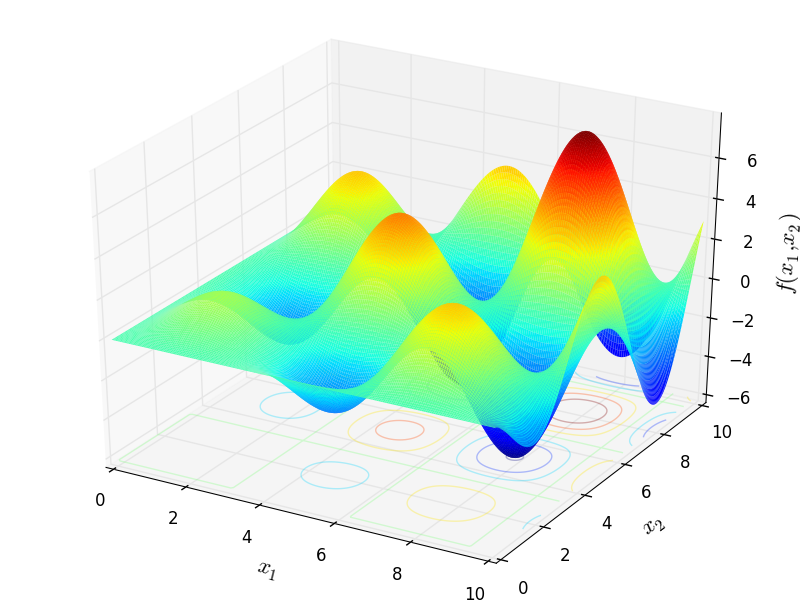
Two-dimensional Alpine 2 function
Global optimum:  for
for 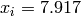 for
for 
AMGM test objective function.
This class defines the Arithmetic Mean - Geometric Mean Equality global optimization problem. This is a multimodal minimization problem defined as follows:
![f_{\text{AMGM}}(\mathbf{x}) = \left ( \frac{1}{n} \sum_{i=1}^{n} x_i - \sqrt[n]{ \prod_{i=1}^{n} x_i} \right )^2](_images/math/d1c2373a4dba6366581a2cb780c6923a34b4b4bf.png)
Here,  represents the number of dimensions and
represents the number of dimensions and ![x_i \in [0, 10]](_images/math/04492218e68759ff19d07231a62fe3a092015dfc.png) for
for  .
.
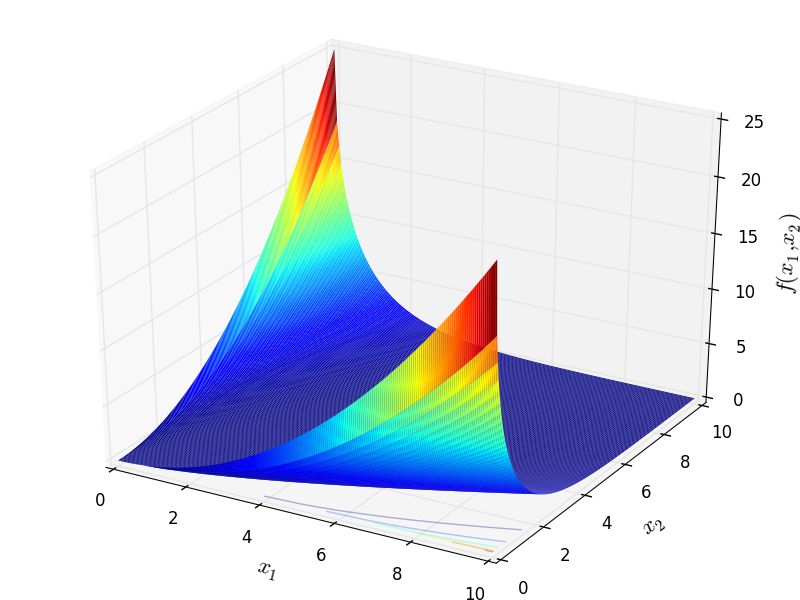
Two-dimensional Arithmetic Mean - Geometric Mean Equality function
Global optimum:  for
for 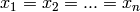 for
for 